水下隧道最小覆巖厚度的理論分析
陳 寧
(1.江西理工大學土木與測繪工程學院,贛州 341000;2.江西省環境巖土與工程災害控制重點實驗室,贛州 341000)
0 引言
從已經存在的知識體系中包括圍巖的古典散體理論還是圍巖的彈塑性理論[1]都認為圍巖坍塌能夠自行穩定,自行穩定后的圍巖具有一定的自承能力。圍巖坍塌能夠自行穩定是因為圍巖內部有一個應力平衡的過程,這種平衡過程是由圍巖內部作用力與反作用力形成的,作用力是圍巖自身的重力與構造力,反作用力是圍巖自身的抵抗作用力,也就是圍巖的自承作用。圍巖內部的反作用力結構就是圍巖的自承結構。
1 圍巖中的自承體系結構
圍巖自穩自承結構的形式[2]:對石質圍巖的結構形式來說,由于巖體受層理、節理、開挖爆破等各種因素的影響,在塑形圍巖區內大多都是不均勻的塊體,隨著洞室的開挖,這些大小不等的塊體在圍巖應力重分布的作用下存在位移變化,在位移變化過程中,巖體塊體間互相作用、互相組合,從而形成一種具有一定承載能力的結構形式。這種結構形式,就是圍巖的自承結構體。
對水下隧道來說,隧道能夠穩定,是因為圍巖中存在有一定結構的自承體系,使得圍巖能穩定,支護系統也屬于自承體系的一部分,因為支護、尤其是錨噴支護往往是與圍巖結成一體的。由許多因素決定自承體系的范圍,巖石隧道的圍巖體系通常只是幾米寬,在土質隧道中圍巖體系可達到20-30米寬。隧道洞形、支護形式和開挖方法都會對自承體系的范圍造成影響。
2 拱頂彎矩公式的推導
由于圍巖的自承結構體是拱形,可建立如下所示計算模型

圖1 水下隧道自承拱計算模型圖
圖中qn為豎向壓力,λqn為水平壓力,q 為作用在自承拱上的水壓力
通過求結構力學[3]解結構內力可得:
2.1 x1=1 單位荷載作用時,拱的截面任意位置的彎矩為:

拱腳處的水平位移為:
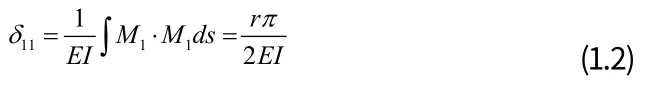
(2)x1=0 時 外荷載單獨作用在拱上
隧道自承拱拱腳處豎直方向的支座反力為:
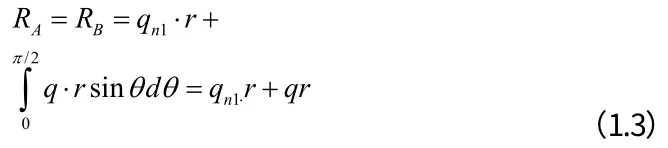
隧道自承拱拱腳處的水平方向支座反力為:

則對于隧道自承拱任意一點的彎矩為:
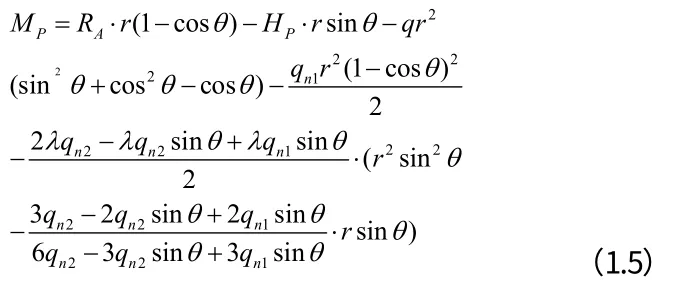
拱腳處的水平位移△1p為:
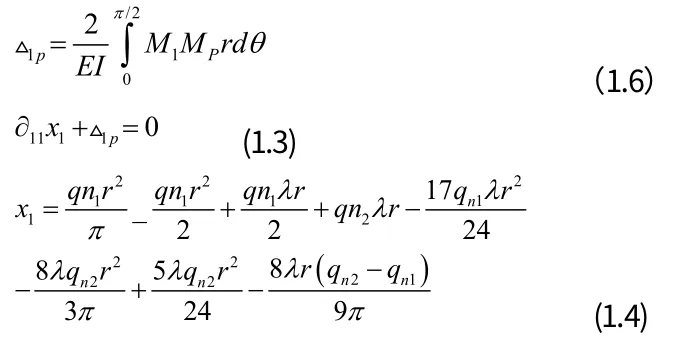
3 自承拱厚度公式的推導
根據結構的對稱性判斷,最大彎矩發生在拱頂處,即:
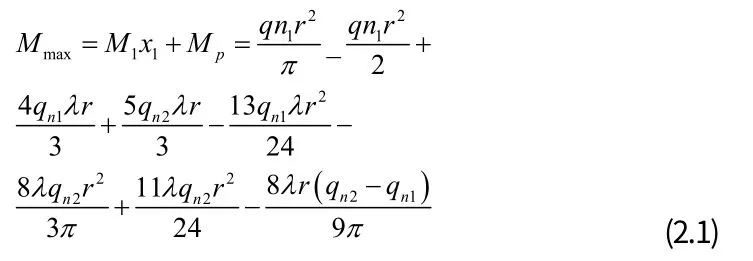
再由材料力學[4]可知,結構受彎矩作用時,其彎矩在結構上產生的拉應力為:

式中,σ1為結構的最大拉應力,Mmax為結構最大彎矩,Wz為抗彎截面系數。
對于抗彎截面系數Wz,因界面是彎矩,其慣性矩Iz=,故Wz=
又因為該計算模型為平面應變模型,所以結構在縱向的尺寸b=1。如隧道圍巖自承拱不破壞,則應滿足下式:
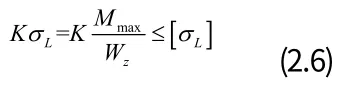
式中σL為圍巖的抗拉強度,K 為安全系數
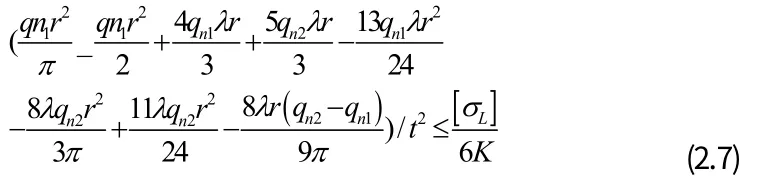
由上式可得隧道圍巖自承拱厚度:
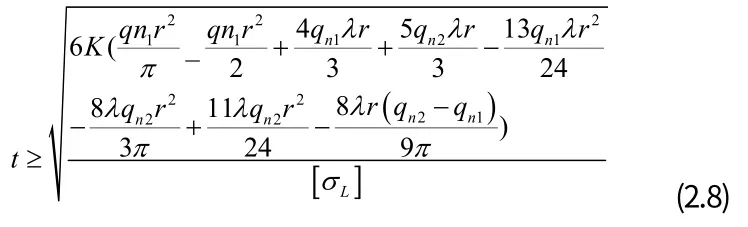
式中,t 為圍巖自承拱厚度,qn1為上覆巖層豎向壓力,qn2為上覆巖層水平壓力,λ為側壓系數,λ=,r 為隧道開挖半徑,H 為隧道覆巖厚度,[σ L]為圍巖的抗拉強度,K 為安全系數,一般取2~3。
隧道圍巖上覆巖層豎向壓力采用礦山法確定,礦山法是依據大量的隧道施工塌方資料進行統計分析計算,提出的一種確定隧道圍巖豎直均布壓力公式。[5]
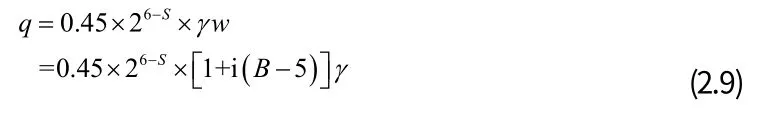
式中 q:圍巖豎直均布壓力(km/m3);
S:圍巖類別,如屬IV 級圍巖,則S=5;
W:寬度影響系數,w=1+i(B+5);
i:圍巖壓力的增減率,當B 5m 時,i=0.2;當B 5m 時,i=0.1;
B:隧道跨度,以B=5 為基本跨度;
4 將公式應用于實際工程
水下隧道在施工過程種最常遇到的是II~V 級,經過超前支護的V 級圍巖,其物理力學參數可達到IV 級圍巖的水平。參考《公路隧道設計規范》II~IV級圍巖的物理力學參數[6]。
以國內外主要公路、鐵路海底隧道為例,
將各參數和半徑r 代入式2.16 中,得出在不同圍巖級別下各隧道的隧道半徑和圍巖自承拱厚度關系圖。
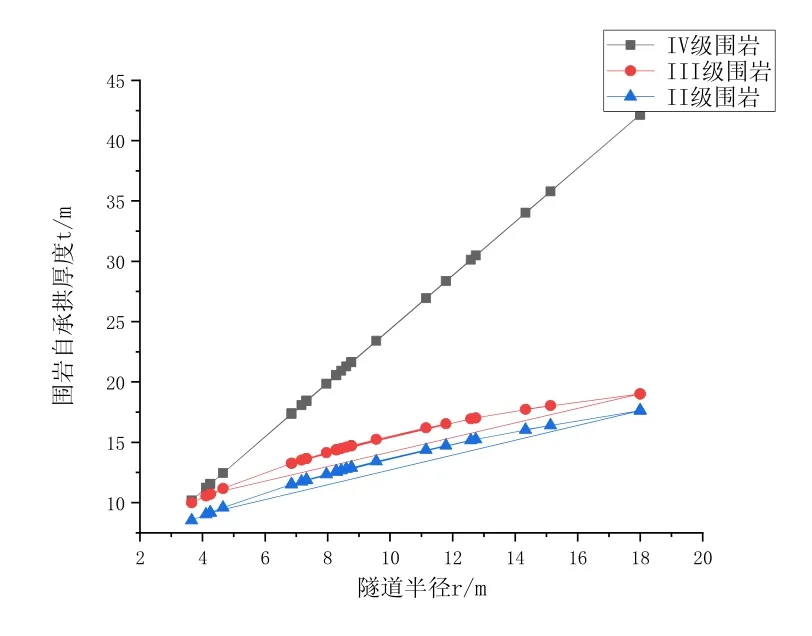
圖3.1 隧道半徑-圍巖自承拱關系

圖3.2 II 級圍巖下拱頂厚度與最小覆巖厚度的關系
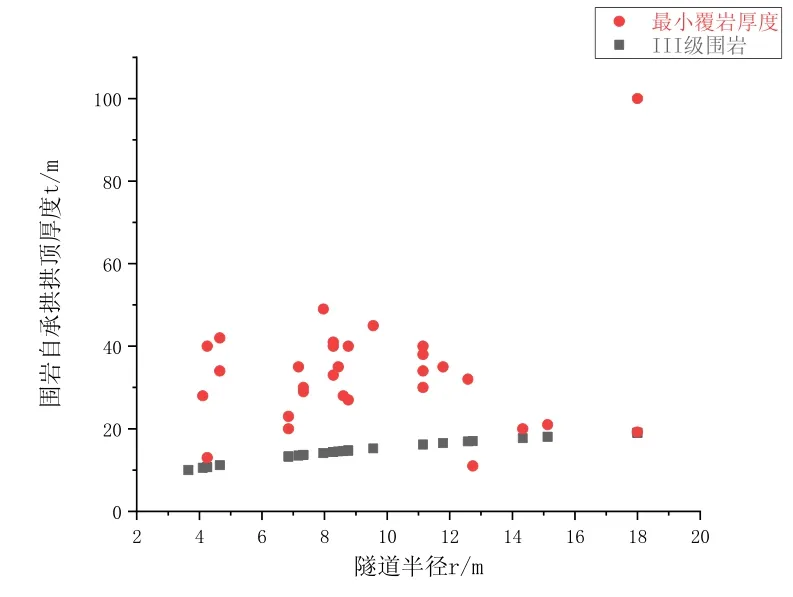
圖3.3 III 級圍巖下拱頂厚度與最小覆巖厚度的關系
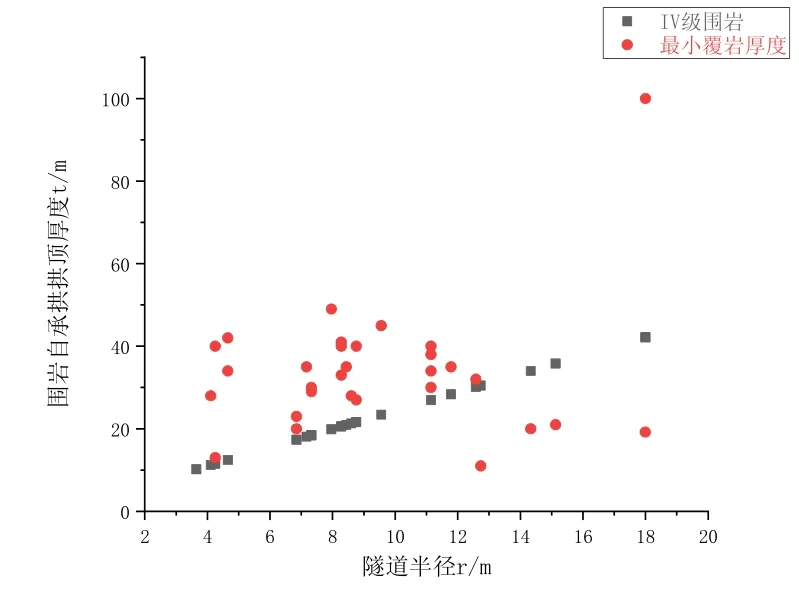
圖3.4 IV 級圍巖下拱頂厚度與最小覆巖厚度的關系
由圖3.1、3.2、3.3、3.4 可知
①:在同一圍巖級別下,隧道半徑如果越大,則圍巖自承拱厚度也越大。
②:在半徑相同的情況下,圍巖級別越高,則隧道圍巖自承拱的厚度也就越大。
③:由于上述隧道大多都是建造完成于上個世紀,所以會有技術上的限制,在最小覆巖厚度的選擇中也會偏于保守。各級圍巖的拱頂厚度與各隧道的最小覆巖厚度呈正相關,可得出該隧道拱頂厚度值作為隧道覆巖厚度的臨界值具有一定的參考價值。
5 將公式應用于蓉江四路隧道
根據該工程初步設計可知,贛州蓉江四路隧道擬用雙向六車道,隧道水下段主要通過中風化粉質泥巖地層,以IV 級圍巖為主,采用鉆爆法施工,開挖跨度為12.5m,圍巖重度為20KN/M3,該隧道的圍巖抗拉強度為1.01MPa,泊松比為0.38,圍巖的滲透系數k=1.68m/d。
依據前文推導出的隧道圍巖自承拱厚度公式2.16 可得:
在IV 級圍巖條件的情況下,蓉江四路隧道的最小覆巖厚度為17.38m。
6 結論
本文利用了結構力學和材料力學的強度理論分別對隧道的自承拱厚度進行理論公式的推導,從而得出以下結論:
(1)在同一圍巖級別下,隧道半徑如果越大,則圍巖自承拱厚度也越大。
(2)在半徑相同的情況下,圍巖級別越高,則隧道圍巖自承拱的厚度也就越大。
(3)水下隧道覆巖厚度隨隧道開挖跨度的增加而增長,在相同覆巖厚度的情況下,開挖跨度越大,隧道越不穩定,與隧道的實際情況相符。最后,本文推導的理論公式用于依托工程—贛州蓉江新區過江隧道,經理論公式推導可得該隧道的最小埋深為17.38 米,但是理論公式的正確性還需進一步驗證,如采用數值模擬和工程類比的計算方法。

