基于GA_BP神經網絡的地鐵車站深基坑變形預測研究
(河南科技大學應用工程學院,河南 三門峽 472000)
0 引言
地鐵車站深基坑工程由于開挖工期長、施工難度大、地質條件和周邊環境復雜、施工過程中各種不確定的因素多等特點,致使地鐵車站深基坑工程施工具有很高的風險性,為了保證工程施工順利實施,開展變形監測和預測工作具有重要的意義。近年來,諸多學者運用時間序列、灰色系統、ARMA模型、BP 神經網絡等多種方法進行基坑監測數據的處理及預測。BP 神經網絡在非線性映射、自適應學習、輸入輸出靈活等方面具有優良性能,因而被廣泛應用于基坑變形預測。但通過研究發現,BP 神經網絡在應用過程中出現收斂速度慢、容易陷入局部極小值、隱含層神經元不確定等不足,而導致預測結果不理想。基于此,本文以鄭州市地鐵5 號線某車站深基坑變形監測實測數據為基礎,利用GA 遺傳算法在全局尋優上的強大搜索能力,優化BP神經網絡,避免預測過程陷入局部極小,通過工程實證分析,表明GA_BP組合預測模型能夠有效提高預測精度。
1 變形預測BP 神經網絡
1.1 變形預測BP 神經網絡模型簡介
變形預測BP 神經網絡是一種人工神經網絡的誤差逆向傳播訓練算法[1],其學習過程由信號的正向傳播和誤差的反向傳播兩個過程構成,正向傳播時,在輸入層輸入樣本數據,經過隱含層處理后,傳向輸出層,若輸出層的實際輸出與變形監測實際值不符時,則轉向誤差反向傳播階段,將輸出誤差通過隱含層向輸入層傳播,并將誤差分攤給各層的神經元,獲取各層神經元的誤差信號,作為修正各個神經元權值的重要依據[2]。BP 神經網絡的拓撲結構如圖1所示。
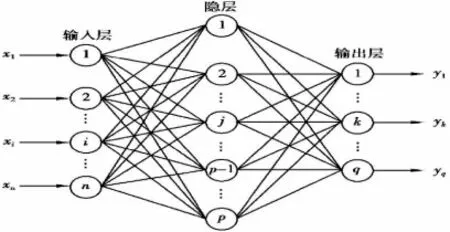
圖1 BP 神經網絡拓撲結構圖
1.2 BP 神經網絡預測模型的缺陷
BP 神經網絡預測模型算法決定了誤差函數存在多個局部極小值,不同的網絡初始權值直接決定了BP 神經算法在收斂于局部最小值還是全局最小值,則會產生不同的預測結果。因此,為了得到理想的預測結果,必須通過計算來確定收斂于全局極小值的網絡初始權值,遺傳算法優化BP 神經網絡能夠解決初始權值選取問題。
2 基于遺傳算法的GA-BP 神經網絡
遺傳算法主要基于Darwin 的進化論和Mendel 的遺傳學說,Darwin 的進化論的核心觀點是適者生存,Mendel 的遺傳學說的主要觀點是基因遺傳原理Mendel 的遺傳學說[3]。它從一組隨機產生的初始解開始訓練、優化,通過對遺傳序列的選擇、交叉以及變異篩選,保留下來適應度好的個體,新的群體不僅繼承了上一代的優點,又使得新的群體優于上一代,如此反復循環,最后收斂于最適應環境的某個個體上,既得到了問題的最優解[1][4]。遺傳算法的實施流程圖如圖2所示。
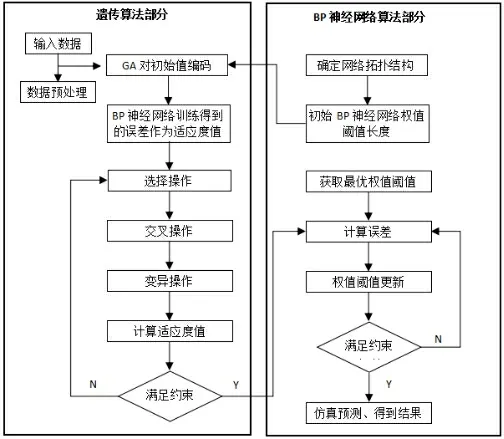
圖2 遺傳算法的實施流程圖
3 工程案例
3.1 工程概況
鄭州地鐵5 號線某車站結構型式為地下三層三跨箱型框架結構,島式車站,站臺寬13m,有效站臺長度140m,車站外包總長170.2m,標準段外包總寬22.3m。車站頂板覆土4.0m,主體結構標準段基坑深24.0m,寬22.3m;盾構井段基坑深25.7m,寬26.5m。擬建工程場地屬于A 區地貌,車站在開挖過程中不可避免會對周圍地層、地下管線、建(構)筑物等造成影響,為了保證施工期間道路暢通,周邊環境安全穩定以及工程結構自身安全,必須對監測數據進行預測,指導施工和改進設計方案。
3.2 模型建立
取地面沉降監測點DBC-9-3 2016年3月4日到2016年7月22日的累計變形監測數據作為訓練樣本,建立深基坑地表沉降經遺傳算法優化的BP神經網絡模型,并運用該模型對DBC-9-3監測點7月29日、8月5日、8月12日的累計變形量進行預測。首先利用遺傳算法優化BP算法程序尋找全局最優解,確定最優的初始權值和閾值,然后利用選取的訓練樣本訓練該神經網絡,達到預設的約束條件后,利用該模型進行預測。輸入值為前三期累計變形量、隱含層節點數設為5、輸出值為第四期累計變形量,以此類推,迭代次數設為200。計算結果如表1所示。
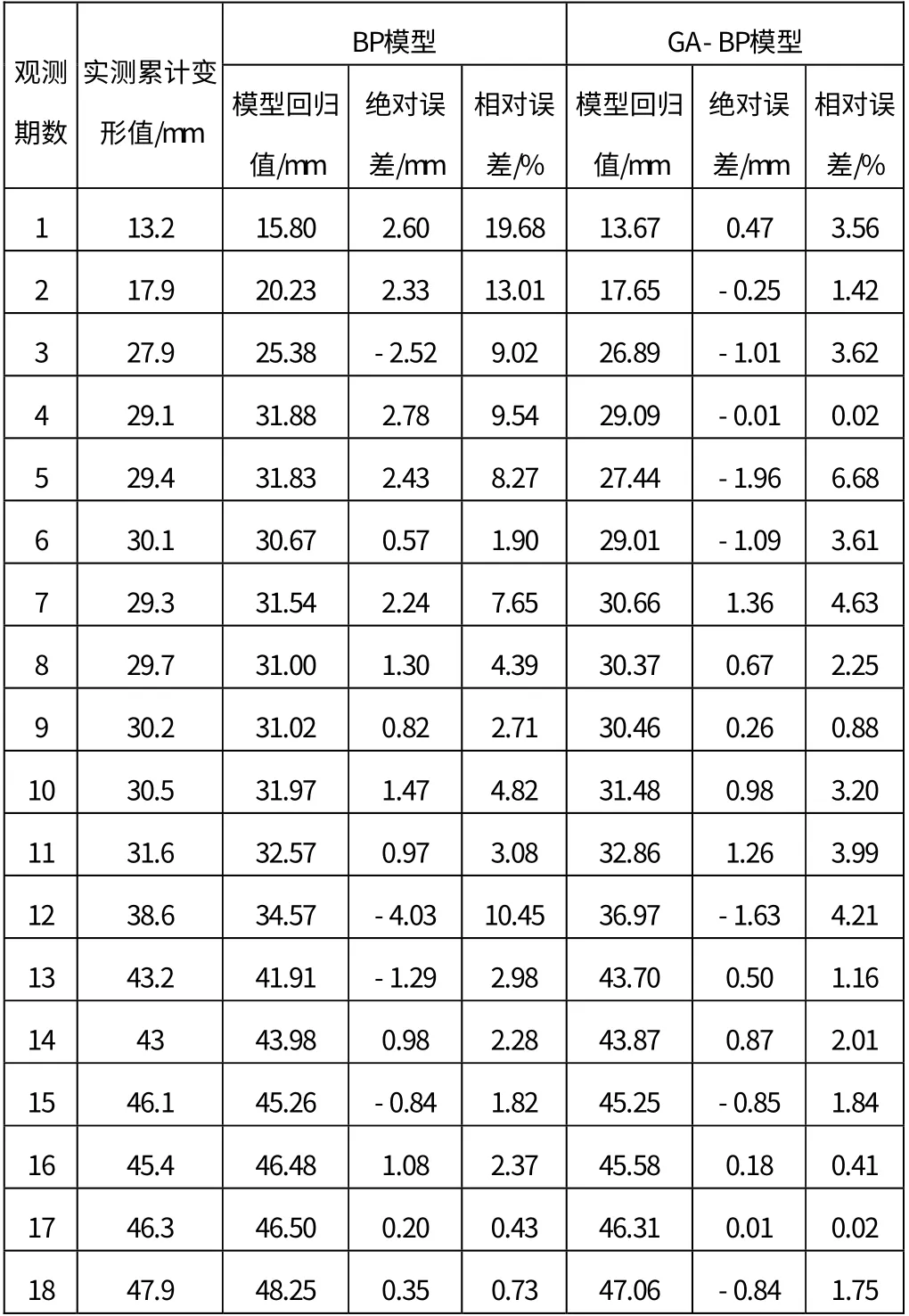
表1 GA-BP模型與BP模型回歸值對比
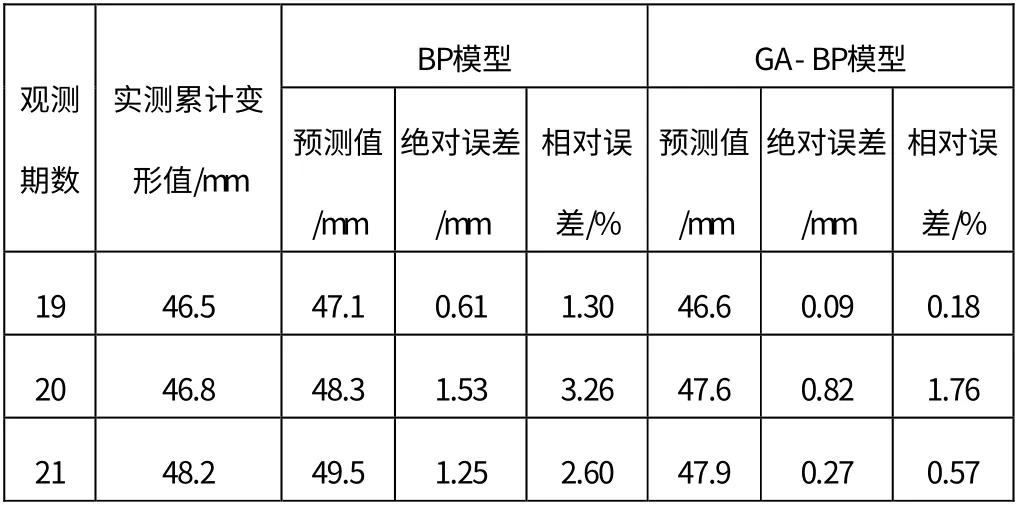
表2 GA-BP模型與BP模型預測對比
3.3 結果分析
通過表1、表2可以看出,BP 神經網絡模型模擬最大絕對誤差值為-4.03mm,最大相對誤差為19.68%,模擬值相對誤差平均值為5.84%,相關系數R2為0.9690,模型預測最大絕對誤差為1.53mm,最大相對誤差為3.26%;GA-BP 模型模擬最大絕對誤差值為-1.96,最大相對誤差為6.68%,相關系數R2為0.9902,模型預測最大絕對誤差為0.82mm,最大相對誤差為1.76%。從上述數據可以看出,GA-BP 神經網絡模型能夠有效提高預測精度。
4 結論
(1)采用經過遺傳算法優化的BP 神經網絡模型來預測地鐵車站深基坑施工周邊地表沉降值,誤差小,收斂速度快,證明該模型與方法分析此類時間序列數據有較好的適用性和準確性。
(2)GA-BP 模型精度很大程度上依靠訓練樣本的數量,訓練樣本越多,預測精度就越高,應該及時將新的監測信息添加到訓練樣本中,及時更新模型以便得到更好的預測效果。

