基于改進PSO-ARIMA模型的船舶縱搖角度預測

王培良　張婷　肖英杰

摘要：

針對自回歸移動平均（auto regressive moving average， ARMA）模型在船舶縱搖角度預測時不具有普遍適用性問題，提出使用自回歸綜合移動平均（auto regressive integrated moving average， ARIMA）模型進行縱搖角度預測，并采用改進粒子群優化（particle swarm optimization， PSO）算法對模型定階。對縱搖角度值序列數據進行平穩性檢驗和差分運算，確定ARIMA模型的適用性;采用具有針對性適應度評價函數的PSO算法進行模型定階，并優化PSO算法的權重計算方法。通過仿真對比驗證本文所提方法的科學性和有效性。仿真結果表明：采用改進PSO算法進行模型定階的方法能夠有效提升模型的預測精度，具有更好的預測效果。

關鍵詞：

自回歸綜合移動平均（ARIMA）模型; 粒子群優化（PSO）算法; 船舶縱搖; 縱搖預測

中圖分類號：? U661.32+1

文獻標志碼：? A

收稿日期： 2020-07-15

修回日期： 2020-09-22

基金項目： 國家自然科學基金（51909155）;濰坊市科學技術發展計劃（2019GX075）

作者簡介：

王培良（1987—），男，山東濰坊人，博士研究生，研究方向為載運工具運用工程，（E-mail）gfy5216@126.com;

張婷（1987—），女，山東聊城人，講師，碩士，研究方向為航海技術，（E-mail）titi-507@163.com;

肖英杰（1959—），男，廣東潮陽人，教授，博導，船長，研究方向為航海技術，（E-mail）xiaoyj@shmtu.edu.cn

Prediction of ship pitch angle based on improved PSO-ARIMA model

WANG Peiliang1，2a，2b， ZHANG Ting3， XIAO Yingjie2a，2b

（1.School of Intelligent Manufacturing， Weifang University of Science and Technology， Weifang 262700， Shandong， China;

2.a.Merchant Marine College; b.Engineering Research Center of Shipping Simulation，

Ministry of Education， Shanghai Maritime University， Shanghai 201306， China;

3.Navigation College， Shandong Transport Vocational College， Weifang 261206， Shandong， China）

Abstract：

In view of the fact that the auto regressive moving average （ARMA） model is not of the universal applicability when predicting the ship pitch angle， an auto regressive integrated moving average （ARIMA） model is proposed for predicting the ship pitch angle， and an improved particle swarm optimization （PSO） algorithm is adopted to determine the model order. For the pitch angle value series， the stationarity test and difference operation of the data are performed to determine the applicability of the ARIMA model. The PSO algorithm with a targeted fitness evaluation function is used to determine the model order， and the weight calculation method of the PSO algorithm is optimized. The scientificity and effectiveness? of the method proposed in this paper is verified through the simulation. The simulation results show that the method using the improved PSO algorithm determining the model order can effectively improve the prediction accuracy of the model and makes the model have better prediction effect.

Key words：

auto regressive integrated moving average （ARIMA） model;particle swarm optimization（PSO） algorithm; ship pitch; pitch prediction

0 引 言

船舶航行時受到外界環境（如風、浪、流等相互作用）的影響，產生六自由度的搖擺運動，嚴重威脅船舶的航行安全，因此，針對船舶搖擺隨時間變化規律的預測研究是航運界的研究難點和熱點[1]。

時間序列分析法是將預測對象的相關屬性值按照時間順序排列，然后結合數學模型研究其屬性變化規律，從而對屬性值進行預測[2-3]。文獻[4]通過在護衛船上安裝傳感器采集數據，采用自回歸移動平均（auto regressive moving average， ARMA）模型進行了船舶橫搖姿態預報;文獻[5]采用自回歸（auto regressive， AR）模型，對船舶縱搖運動進行了自適應預報研究;文獻[6]以艏前波法為基礎，采用ARMA模型對船舶運動姿態進行了短時間高精度預報研究;文獻[7]以船模水池實驗為研究背景，使用線性AR模型進行船舶運動預報研究;文獻[8]在AR模型的基礎上，使用卡爾曼濾波算法對模型參數進行估計，對船舶運動進行實時估計，提高了模型預報的速度和精度;文獻[9]使用AR模型對船舶運動進行預測，并使用格型遞歸最小二乘法對模型參數進行估計，提高了預報速度。

綜上，在基于相關屬性時間序列對船舶運動進行研究時[10]，AR模型[11]、ARMA模型等均能夠進行有效預測，優化模型參數也對預測結果具有明顯影響。然而，航行環境的隨機性和波動性使得船舶縱搖角度值時間序列為方差、均值均存在變化的非平穩序列，因此，本文使用自回歸綜合移動平均（auto regressive integrated moving average， ARIMA）模型對船舶的縱搖角度進行預測，并且使用粒子群優化（particle swarm optimization， PSO）算法

進行模型定階[12]，確定最優的ARIMA[13-14]模型并進行相應的縱搖角度預測。

1 理論與方法

1.1 ARIMA模型

ARIMA模型于20世紀70年代由BOX-JENKINS提出，其本質是將每個預測對象與相應的時間連接構建時間序列，用準確的數學模型描述該時間序列，并根據時間序列的性質預測未來值。記一個按時間順序排列的隨機事件序列為{xt}，則ARIMA（p，d，q）模型的表達式為

xt=1xt-1+2xt-2+…+pxt-p+

δ+εt+θ1εt-1+θ2εt-2+…+θqεt-q（1）

式中：p為AR模型的自回歸項數;d為差分階數;q為移動平均（moving average， MA）模型的移動平均項數;δ為常數項（表示序列數據沒有零均值變化）;

{εt}為白噪聲序列，其均值和方差分別為E（εt）=0

和D（εt）=σ2;i和θj（i=1，…，p;j=1，2，…，q）分別是xt和εt的參數，可用最大似然法等進行估計。

1.2 PSO算法

20世紀90年代初，Kenndy和Eberhart提出了PSO算法。該算法源于對鳥類捕食行為的研究：當鳥類捕食時，對每只鳥而言尋找食物最簡單有效的方法就是搜索當前離食物最近的鳥所在的區域及周圍區域。在PSO算法中，每個粒子代表一只鳥，同時代表所求問題的一個潛在解，每個粒子都有一個由適應度函數評價出的適應度值，用來表示當前解的優劣;同時粒子本身具有速度，其決定了粒子移動的方向和距離，速度根據自身及周圍粒子的移動狀態進行更新調整，從而實現全局尋優。算法在D維空間進行搜索，d=1，2，…，D。在每次迭代過程中，粒子i的速度和位置更新公式[15]如下：

式中：

k為當前迭代次數;

Pid，k為個體極值;Pgd，k為全局極值;vid，k為當前時刻粒子i的速度分量;

xid，k為當前時刻粒子i的位置分量;ω為慣性權重;加速度因子c1和c2為非負常數;

r1和r2為[0，1]內的隨機數。

慣性權重ω的大小對算法的搜索能力具有顯著影響：其值較大時，有利于全局搜索;其值較小時，有利于局部搜索。因此，為有效平衡全局搜索與局部搜索能力，使用線性遞減權重：

ωk=ωk-（ωs-ωe）k/Tmax（3）

式中：ωs為慣性權重初始值;ωe為最大迭代次數時的慣性權重值;Tmax為最大迭代次數。

因此，迭代初期的較大權重值使算法保持較強的全局搜索能力;隨著迭代的不斷進行，慣性權重值逐漸減小，有利于算法進行準確的局部搜索。

1.3 ARIMA模型定階

采用似然函數進行參數估計時，若數據樣本量大，則能夠不斷提高模型的精度，但模型的復雜度也隨之提升，同時帶來參數估計中常見的過擬合現象。因此，需要對模型進行定階。模型定階也被稱為模型識別，指確定ARIMA模型（式（1））中的p、q值。一般模型定階采用AIC或者BIC準則，但有時其最終結果并非全局最優，因此，本文將這2個參數作為PSO算法的粒子位置信息進行優化求解，獲得參數最優值及最優組合。

在使用PSO算法進行參數優化時，用適應度函數作為評價粒子性能優劣的主要指標，適應度值越大，參數值越符合模型。常采用均方誤差或均方根誤差評價ARIMA模型預測效果，因此，本文根據其思想設定適應度函數為

f（x）=1ni=1（yi-y^i）2（4）

式中：n為粒子數目;yi和y^i分別為研究對象的實際值和預測值。

由式（4）可知，預測值與實際值之間的差值越小，則適應度值越大，這說明粒子越合適，模型越理想，預測效果越好。

1.4 ARIMA模型構建流程

在使用ARIMA模型對船舶縱搖角度進行預測時，需要對縱搖角度值時間序列分別進行平穩性、白噪聲等檢驗，確保研究對象的嚴謹，其具體步驟為：

①獲得船舶縱搖角度值原始時間序列，并檢查其平穩性;②若原始序列為非平穩序列，則對其進行差分運算，然后進行平穩性和白噪聲檢驗;

③根據差分之后的平穩、非白噪聲序列進行ARIMA模型擬合，使用PSO算法進行參數優化;④使用擬合獲得的ARIMA模型進行研究對象的預測。

ARIMA模型構建流程見圖1。

2 實驗結果及分析

2.1 平穩性檢驗

為驗證本文所提方法的科學性和有效性，以某船船首處的縱搖角度值為研究對象。該船為低速單機柴油機驅動、單槳、單舵船，屬尾機型、方尾船型，其基本參數見表1。

在船舶航行過程中采集數據47次，每次采集100個樣本值，以最后5次均值數據為檢驗序列，前42次均值數據為原始值序列，見圖2。

分析圖2可知，船首處的縱搖角度值序列存在非平穩性;通過計算得出序列的單位根檢驗統計量對應的P值為0.643 1，顯著大于0.05。因此，原縱搖角度值序列為非平穩序列，需要對其進行差分，從而確定ARIMA模型參數d。

2.2 差分運算及白噪聲檢驗

差分后的縱搖角度值序列見圖3a。分析圖3可知：差分后的縱搖角度值序列趨于平穩，其單位根檢驗統計量對應的P值為0.001，顯著小于0.05，且自相關圖也顯示出短期相關性，因此可將差分后的縱搖角度值序列看作平穩序列。同時，基于殘差的白噪聲檢驗統計量為0.012 2，未明顯大于顯著水平，因此，可以認為差分后的縱搖角度值是平穩、非噪聲序列。

2.3 模型定階及預測分析

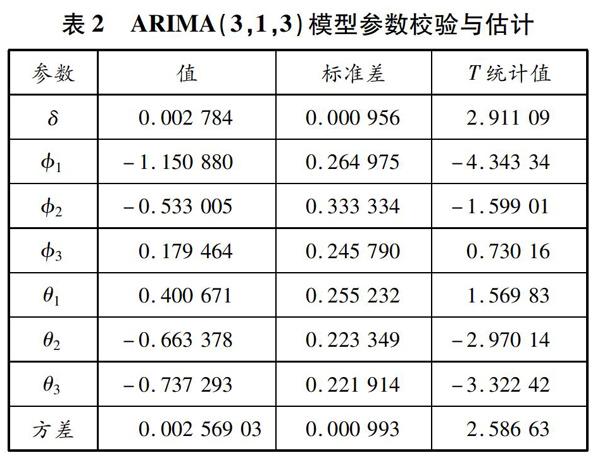
基于式（4）使用PSO算法進行計算，最終獲得模型參數值分別為p=3、d=1、q=3，從而確定預測模型為ARIMA（3，1，3）。ARIMA（3，1，3）模型參數校驗與估計見表2。

用ARIMA（3，1，3）模型進行預測，其結果見圖4。由圖4可知，ARIMA模型能夠實現船首處縱搖角度值的預測，且實際值與預測值總體相差較小，表明預測模型較為準確，模型參數設置較為合理。

為驗證利用PSO算法定階的優勢，采用傳統BIC準則給ARIMA模型定階，得到ARIMA（4，1，3）模型。將基于PSO算法定階的ARIMA（3，1，3）模型與ARIMA（4，1，3）模型的預測結果進行對比，見圖5。由圖5可知：ARIMA（4，1，3）模型也能對船舶縱搖角度進行預

測，但其預測效果比ARIMA（3，1，3）模型的差;

兩者在時間點3處的預測值均出現振蕩。為進一步顯示本文所提方法的優勢，使用均方根誤差（root mean squared error， RMSE）反映預測精度：ARIMA（3，1，3）模型預測結果的RMSE為0.037 94，小于ARIMA（4，1，3）模型預測結果的RMSE（0.057 24），這說明本文所述方法能夠有效提升ARIMA模型的預測精度。

3 結 論

針對船舶縱搖角度值時間序列的非平穩性，采用自回歸綜合移動平均（ARIMA）模型進行縱搖角度預測，并使用對慣性權重進行改進的粒子群優化（PSO）算法進行模型定階，設計適應度評價函數。通過仿真實驗對比采用PSO算法定階得到的ARIMA模型與采用傳統BIC準則定階得到的ARIMA模型的預測精度，結果表明：改進的PSO算法通過針對性的適應度評價函數能夠提高ARIMA模型的預測精度，驗證了本文所提方法的科學性和有效性。

參考文獻：

[1]王培良， 吳曉芳， 張婷. 在航集裝箱船搖擺姿態的概率模型[J]. 上海海事大學學報， 2017， 38（4）： 21-25. DOI： 10.13340/j.jsmu.2017.04.005.

[2]張騰， 任俊生， 范小晴， 等. 基于多系數保角變換法的船舶垂蕩縱搖運動仿真[J]. 上海海事大學學報， 2019， 40（3）： 51-56. DOI： 10.13340/j.jsmu.2019.03.009.

[3]馬建文， 涂興華， 吳小峰， 等. 多自由度本船操縱運動仿真[J]. 上海海事大學學報， 2016， 37（4）： 32-35. DOI： 10.13340/j.jsmu.2016.04.006.

[4]BROOME D R， HALL M S. Application of ship motion prediction[J]. International Maritime Technology， 1998， 10（1）： 77-93.

[5]翁震平， 顧民， 劉長德. 基于二階自適應Volterra級數的船舶運動極短期預報研究[J]. 船舶力學， 2010， 14（7）： 732-740.

[6]程超， 穆榮軍， 蔡玲， 等. 基于遭遇波的艏前波法的航母姿態預報[J]. 中國慣性技術學報， 2015， 23（3）： 409-414. DOI： 10.13695/j.cnki.12-1222/o3.2015.03.024.

[7]馬潔， 韓蘊韜， 李國斌. 基于自回歸模型的船舶姿態運動預報[J]. 艦船科學技術， 2006， 28（3）： 28-30.

[8]彭秀艷， 王茂， 劉長德. AR模型參數自適應估計方法研究及應用[J]. 哈爾濱工業大學學報， 2009， 41（9）： 12-16.

[9]彭秀艷， 劉長德. 基于格型遞歸最小二乘算法的船舶運動極短期預報[J]. 船舶力學， 2012， 16（1/2）： 44-51.

[10]張澤國， 尹建川， 胡江強， 等. 基于減聚類ANFIS模型的船舶橫搖運動實時預測[J]. 上海海事大學學報， 2017， 38（1）： 7-11， 67. DOI： 10.13340/j.jsmu.2017.01.002.

[11]BIANDejun， QIN Shiqiao， WU Wei，et al. A hybrid AR-DWT-EMD model for the short-term prediction of nonlinear and non-stationary ship motion[C]//2016 Chinese Control and Decision Conference. IEEE， 2016： 4042-4047. DOI： 10.1109/CCDC.2016.7531691.

[12]王培良， 張婷， 肖英杰. 蟻群元胞優化算法在人群疏散路徑規劃中的應用[J]. 物理學報， 2020， 69（8）： 240-248.

[13]SUHERMIN， SUHARTONO， PRASTYO D D，et al. Roll motion prediction using a hybrid deep learning and ARIMA model[J]. Procedia Computer Science， 2018： 251-258. DOI： 10.1016/j.procs.2018.10.526.

[14]TOUAMAH Y. Application of the statistical analysis for prediction of the Jordanian GDP by using ARIMA time series and Holts linear trend models for the period （2003-2013）[J]. Mathematical Theory and Modeling， 2014， 4（14）： 19-26.

[15]DINGWeiping， WANG Jiandong， GUAN Zhijin，et al. Cooperative extended rough attribute reduction algorithm based on improved PSO[J]. Journal of Systems Engineering and Electronics， 2012， 23（1）： 160-166. DOI： 10.1109/JSEE.2012.00020.

（編輯 趙勉）