船舶動力設備拆裝過程的網絡模型及復雜性分析

陳登智　江國和　孫久航　劉嬋娟

摘要：

船舶動力設備拆裝是船員適任證書考試的重要環節，為對該考試過程進行智能化評估，將船舶動力設備拆裝過程抽象為以拆裝任務為節點、任務之間聯系為邊的復雜網絡。從網絡整體結構特征和局部特征兩個方面對網絡復雜性進行分析;通過測量網絡節點中心性指標對設備拆裝關鍵任務進行識別;通過計算網絡最短路徑進行任務相關性分析，確定設備拆裝的步驟。以船用6135柴油機吊缸拆卸過程為例，驗證了模型的有效性。本文提出的方法還可為其他機械設備的拆裝和維修過程提供參考。

關鍵詞：

船舶動力設備; 虛擬拆裝; 復雜網絡; 中心性指標; 復雜性分析

中圖分類號：? U664.12

文獻標志碼：? A

收稿日期： 2020-06-01

修回日期： 2020-12-16

基金項目： 國家自然科學基金（11571008）;上海海事大學研究生創新基金（2015ycx076）

作者簡介：

陳登智（1980—），男，湖南衡陽人，助理研究員，博士研究生，研究方向為船舶動力設備拆裝過程建模和智能優化，

（E-mail）dzhchen@shmtu.edu.cn;

江國和（1963—） ，男，江西都昌人，教授，博導，博士，研究方向為動力機械振動噪聲控制，（E-mail）ghjiang@shmtu.edu.cn

Network model and complexity analysis of disassembly and assembly process of marine power equipments

CHEN Dengzhia， JIANG Guohea， SUN Jiuhanga， LIU Chanjuanb

（a. Merchant Marine College; b. Institute of Logistics Science & Engineering， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

The disassembly and assembly of marine power equipments is an important link in the certificate examination of competency for seafarers. In order to evaluate the examination process intelligently， the process of disassembly and assembly of marine power equipments is abstracted into a complex network composed of nodes denoting tasks and connecting lines between tasks. The network complexity is analyzed from the overall structure characteristics and the local characteristics of the network. The key tasks are identifiedby measuring centrality indices of the network nodes. The task correlation is analyzed by calculating the network shortest path， and the process of equipment disassembly and assembly is determined. Taking the process of disassembly of the marine 6135 diesel engine cylinder as an example， the validity of the model is verified. The proposed method can provide reference for the disassembly， assembly and maintenance process of other mechanical equipments.

Key words：

marine power equipment; virtual disassembly and assembly; complex network; centrality index;complexity analysis

0 引 言

船舶動力設備拆裝是船員適任證書考試的重要環節，也是輪機員實踐操作技能的重要體現。然而，目前船員適任證書考試評估仍處于憑經驗評估階段。為對該考試過程進行科學、合理的評估，優化船舶動力設備拆裝過程，本文結合復雜網絡理論對船舶動力設備拆裝過程的復雜性進行分析。

由于船舶動力設備的組成部分各有特點，且各個零部件在質量、尺寸、精度等方面存在差異，若拆裝不當，會使零部件受損，造成不必要的浪費和安全事故。因此，必須對一些復雜的重要零部件進行必要的識別和標記，用以提醒在拆裝過程中嚴防敲擊和注意保護等[1]。目前，國內外學者對船舶動力設備拆裝過程的研究并不多，且多采用SolidWorks模擬設備拆裝過程[2-4]。侯政良等[5]提出了在SolidWorks環境下進行虛擬拆裝的方法，建立了柴油機虛擬拆裝平臺，對某型船用柴油機的拆裝過程進行了模擬。段尊雷等[6]根據實時的系統參數檢測結果和隸屬函數得出模糊關系矩陣，經多重模糊綜合評判得出評估結果。

船舶動力設備是一個由眾多零部件組裝而成的復雜系統，可把每個零部件看作一個拆裝任務，而每個零部件在拆裝過程中的前驅、后繼關系可以抽象為網絡的邊。因此，可以將船舶動力設備拆裝過程抽象為一個以拆裝任務為節點、任務之間聯系為邊的復雜網絡。張青等[7]提出基于慣性動作捕獲設備交互控制關系從而進行虛擬裝配的方法，解決了高精度實時姿態信息收集問題。機械設備的拆裝對設備的保養、檢修、維護和延長生命周期具有重要意義[8]。制定復雜聯動器械的拆裝步驟需要考慮設備穩定性和零部件特征[9-10]。分析設備拆裝過程的復雜性和拆裝過程特征，是設計和優化拆裝過程的基礎[11]。

1998年在《Nature》上發表的《小世界網絡的群體動力學行為》和1999年在《Science》上發表的《隨機網絡中標度的涌現》開啟了復雜網絡研究的新時代，復雜網絡理論開始被廣泛應用于生物學[12]、社會學、醫學[13]、交通[14]等領域。對動力設備的拆裝順序及其制約關系采用網絡進行建模，可以把對拆裝過程復雜性的研究轉換為對網絡本身復雜性的研究。目前，尚未見將復雜網絡應用于動力設備拆裝過程的研究。

基于以上背景，本文應用復雜網絡理論對船舶動力設備拆裝過程的復雜性進行分析。首先構建船舶動力設備拆裝過程的網絡模型，分析整體網絡特征，然后基于復雜網絡理論的中心性指標建立設備拆裝關鍵任務識別模型，并基于網絡最短路徑進行拆裝任務相關性分析，以期為船舶動力設備拆裝過程優化提供新的方法和思路，提高船員適任證書考試評估的科學性和準確性。

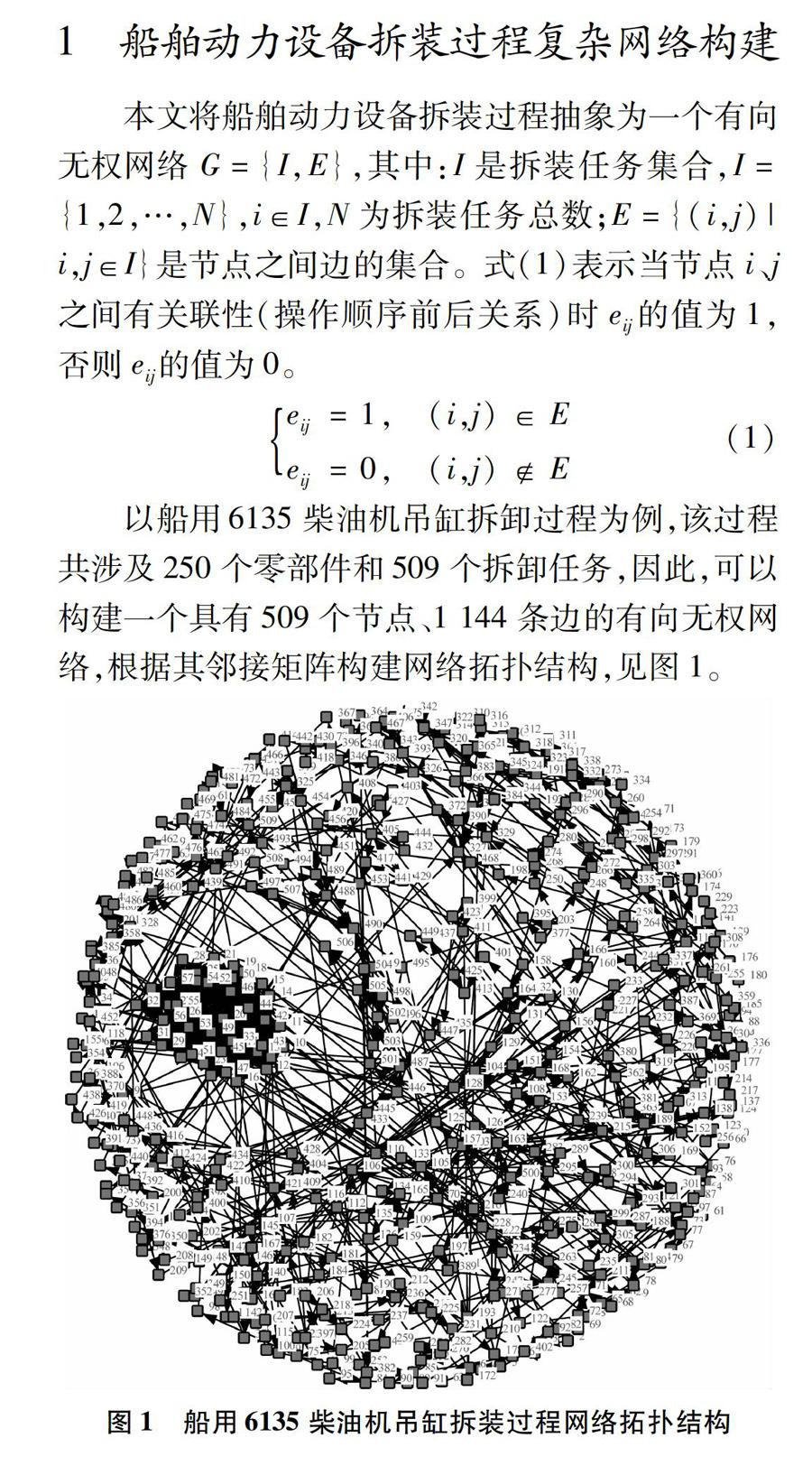
1 船舶動力設備拆裝過程復雜網絡構建

本文將船舶動力設備拆裝過程抽象為一個有向無權網絡G={I，E}，其中：I是拆裝任務集合，I={1，2，…，N}，i∈I，N為拆裝任務總數;E={（i，j）|i，j∈I}是節點之間邊的集合。式（1）表示當節點i、j之間有關聯性（操作順序前后關系）時eij的值為1，否則eij的值為0。

eij=1， （i，j）∈E

eij=0， （i，j）E

（1）

以船用6135柴油機吊缸拆卸過程為例，該過程共涉及250個零部件和509個拆卸任務，因此，可以構建一個具有509個節點、1 144條邊的有向無權網絡，根據其鄰接矩陣構建網絡拓撲結構，見圖1。

2 網絡整體結構分析

在社會網絡理論中，網絡整體結構或多或少會對其中行動者的行為產生影響，即“社會結構”影響“能動作用”。根據船舶動力設備拆裝任務之間的關系計算整體網絡密度、網絡聚集系數和網絡平均最短路徑。

整體網絡密度。網絡密度反映網絡節點之間的聯系程度，網絡密度越大，表明網絡節點之間的聯系越緊密。在一個有向網絡中，若網絡節點數為N，那么這些節點之間包含的關系總數在理論上的最大值為N（N-1）/2，若網絡中包含的實際關系數為M，那么整體網絡密度就是“實際關系數”除以“理論上的最大關系數”：

D=2M/（N（N-1））

（2）

網絡聚集系數。節點聚集系數c（i）表示該節點與其鄰接節點之間的緊密程度;k表示節點i的度;T（i）表示節點i的k個鄰接節點之間可能形成的最大連接邊數;E（i）表示節點i的k個鄰接節點之間的實際連接邊數;整個網絡的聚集系數c（s）為網絡中所有節點的聚集系數的平均值。相關計算式如下：

c（i）=E（i）/T（i）（3）

T（i）=k（k-1）/2（4）

c（s）=Ni=1c（i）/N（5）

網絡平均最短路徑。任意兩個節點i、j之間的最短路徑用其所包含的邊數dij來衡量。整個網絡的平均最短路徑L為網絡中所有節點對之間最短路徑的平均數：

L=2N（N-1）i≥jdij

（6）

計算結果顯示：該網絡的整體網絡密度（0.004）較小，說明它是一個稀疏網絡;各任務之間的集聚性較低（網絡聚集系數為0.073），表明各任務之間互相影響的可能性較小，絕大多數任務具有一定的相對獨立性;該網絡的平均最短路徑約為7.034，說明任意兩個任務之間經過約7個任務的鏈接就會產生間接影響。

3 基于網絡節點中心性指標的設備拆裝關鍵任務識別

中心性是社會網絡分析的研究重點之一，一般衡量網絡節點中心性的指標有度數中心性、接近中心性、中介中心性、特征向量中心性等。本文構建的船舶動力設備拆裝過程網絡為一個有向無權網絡，因此，選取FREEMAN[15]提出的度數中心性、接近中心性和中介中心性指標對網絡節點特征進行分析，用以識別船舶動力設備拆裝過程中的關鍵任務。

3.1 度數中心性

節點i的度數中心性指與節點i直接相連的節點的個數，可以直觀反映該節點與網絡中其他節點發生直接聯系的可能性大小。出度kouti指從節點i指向的其他節點的個數，入度kini指從其他節點指向節點i的節點的個數，其計算公式為

kouti=jeij（7）

kini=jeji（8）

3.1.1 出度

節點i的出度反映該節點對其他節點的影響程度。圖2為6135柴油機吊缸拆卸過程中各任務的出度計算結果和出度概率分布。由圖2a可知，網絡中僅極少數節點的出度較大，大部分節點的出度都在5以下;由圖2b可知，其出度服從階段冪律分布，因此所建網絡為無標度網絡。

表1給出了部分拆卸任務的出度及其排名。由表1可知：任務T6（放缸套水）和T15（拆進氣管）對其他任務的影響最大，其出度均為30，這說明這兩個任務與其后續30個任務都有直接聯系，在設備拆卸過程中，一旦這兩個任務操作過程出現錯誤或者失敗，將導致其后續30個任務也無法完成;任務T111（檢查漏水、漏氣和運行狀況）為最后一個拆卸任務，因此其出度為0。T6和T15的拓撲結構見圖3。

3.1.2 入度

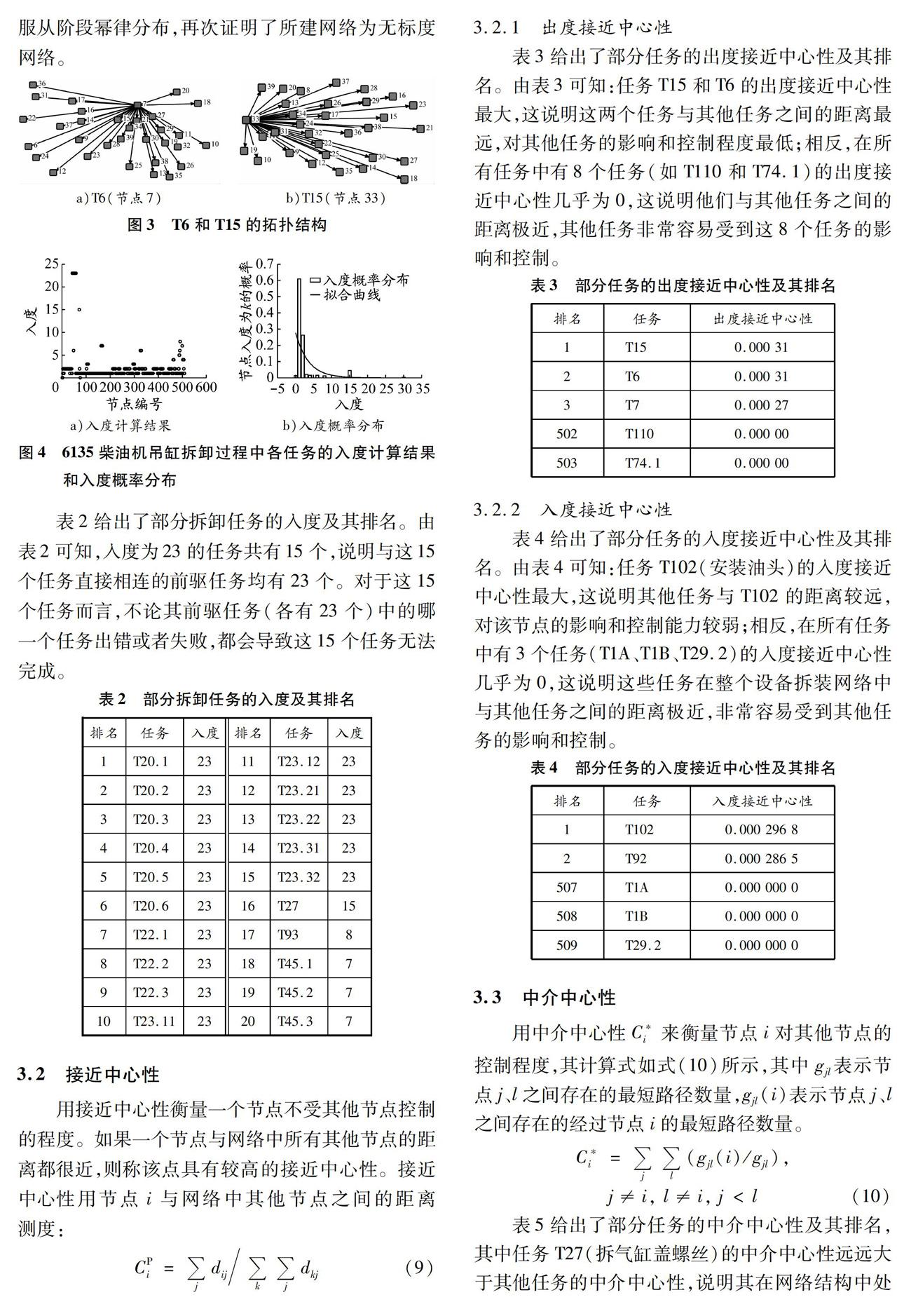
節點j的入度反映該節點受其他節點影響的程度。圖4為6135柴油機吊缸拆卸過程中各任務的入度計算結果和入度概率分布。由圖4a可知，與出度計算結果相似，網絡中僅少數節點的入度較大，大部分節點入度都在3以下;由圖4b可知，其入度也服從階段冪律分布，再次證明了所建網絡為無標度網絡。

表2給出了部分拆卸任務的入度及其排名。由表2可知，入度為23的任務共有15個，說明與這15個任務直接相連的前驅任務均有23個。對于這15個任務而言，不論其前驅任務（各有23個）中的哪一個任務出錯或者失敗，都會導致這15個任務無法完成。

3.2 接近中心性

用接近中心性衡量一個節點不受其他節點控制的程度。如果一個節點與網絡中所有其他節點的距離都很近，則稱該點具有較高的接近中心性。接近中心性用節點i與網絡中其他節點之間的距離測度：

CPi=jdij

k

jdkj

（9）

3.2.1 出度接近中心性

表3給出了部分任務的出度接近中心性及其排名。由表3可知：任務T15和T6的出度接近中心性最大，這說明這兩個任務與其他任務之間的距離最遠，對其他任務的影響和控制程度最低;相反，在所有任務中有8個任務（如T110和T74.1）的出度接近中心性幾乎為0，這說明他們與其他任務之間的距離極近，其他任務非常容易受到這8個任務的影響和控制。

3.2.2 入度接近中心性

表4給出了部分任務的入度接近中心性及其排名。由表4可知：任務T102（安裝油頭）的入度接近中心性最大，這說明其他任務與T102的距離較遠，對該節點的影響和控制能力較弱;相反，在所有任務中有3個任務（T1A、T1B、T29.2）的入度接近中心性幾乎為0，這說明這些任務在整個設備拆裝網絡中與其他任務之間的距離極近，非常容易受到其他任務的影響和控制。

3.3 中介中心性

用中介中心性C*i來衡量節點i對其他節點的控制程度，其計算式如式（10）所示，其中gjl表示節點j、l之間存在的最短路徑數量，gjl（i）表示節點j、l之間存在的經過節點i的最短路徑數量。

C*i=jl（gjl（i）/gjl），

j≠i， l≠i， j

（10）

表5給出了部分任務的中介中心性及其排名，其中任務T27（拆氣缸蓋螺絲）的中介中心性遠遠大于其他任務的中介中心性，說明其在網絡結構中處于中介位置，在整個拆卸過程中起極其重要的作用，想要完成大部分拆卸任務都必須先完成任務T27。

3.4 各種中心性指標計算結果比較

圖5為本文所選取的5種中心性指標計算結果的對比圖。由圖5可知，部分中心性結果的變動過程具有一致性，比如，該網絡節點的入度與中介中心性的變化過程基本一致，入度高的節點也具有較高的中介中心性。

為進一步研究各種中心性指標之間的關系，對5種中心性結果進行標準化處理后，進行相關性分析，結果見圖6。由圖6可知：節點的入度和出度分布集中在低值區域;高出度（入度）節點的入度（出度）較低;高出度節點的入度接近中心性較低，出度接近中心性較高;節點的入度接近中心性與中介中心性負相關，當節點的入度接近中心性增加時，其中介中心性顯著降低。

4 基于網絡平均最短路徑的拆裝任務相關性分析

船舶動力設備拆裝過程網絡的平均最短路徑越短，兩個任務之間的中間環節就越少，涉及的零部件就較少，兩個任務之間的關系就越緊密，任務之間的相關性就越高。通過計算網絡中任意兩個節點之間的最短路徑得到，與節點7、33的最短路徑為1的節點數最多，均為30，說明這兩個節點與網絡中其他節點之間的相關性最大，其子網絡分別見圖7和圖8。

5 結 論

本文將船舶動力設備拆裝過程抽象為以拆裝任務為節點、拆裝任務之間的聯系為邊的復雜網絡。首先，對這個網絡的整體結構進行分析發現：以船用6135柴油機吊缸拆卸過程為例所建的網絡的整體網絡密度較小，是一個典型的稀疏網絡;該網絡的聚集系數也較小，表明各任務之間的集聚性較低，各任務之間互相影響的可能性較小，絕大多數任務具有一定的相對獨立性;該網絡的平均最短路徑約為7.034，即任意兩個任務之間經過約7個任務的鏈接就會產生間接影響。

其次，提出基于網絡節點中心性指標的設備拆裝關鍵任務識別模型。計算結果表明，根據不同中心性指標得到的網絡關鍵任務各不相同，出度最大的任務為T6（放缸套水）和T15（拆進氣管），這兩個任務在整個設備拆卸過程中擁有最多的后續任務，對其他任務的影響程度最大。在實際操作中，放缸套水和拆進氣管都是進行其他操作的必要步驟，進一步驗證了該結論與實際操作情況相符。入度最大的節點有15個，其入度均為23，說明這15個任務都擁有23個前驅任務，故這15個任務在整個設備拆裝過程中都受相應的23個前驅任務的影響，拆卸操作難度最大。出度接近中心性最大的任務為T6 和T15，說明這兩個任務與網絡中其他任務之間的距離較遠，因此他們對其他任務的影響和控制程度最低。入度接近中心性最大的任務為T102（安裝油頭），說明網絡中其他任務與任務T102的距離最遠，對該任務的影響和控制能力比較弱。任務T27（拆氣缸蓋螺絲）的中介中心性遠遠大于其他任務的中介中心性，說明其在網絡結構中處于中介位置，在整個拆卸過程中起極其重要的作用，想要完成大部分拆卸任務都必須先完成任務T27。

最后，通過對網絡最短路徑分析發現，與節點7、33的最短路徑為1的節點數最多，均為30。這說明這兩個任務與網絡中其他任務之間的相關性最大。

本文將船舶動力設備拆裝過程抽象為一個網絡，采用復雜網絡分析研究這個網絡的復雜性，以此反映拆裝過程的復雜性，有別于直接研究拆裝序列，是一種通過網絡統計揭示拆裝過程復雜性的新的嘗試。因此，通過該文提出的方法，能夠分析和評估拆裝過程本身的復雜性。對網絡節點中心性指標的分析能夠識別和評價關鍵拆裝任務對整個拆裝過程的影響。下一步將進行船舶動力設備拆裝過程路徑智能優化。本文在實踐層面有利于明晰船舶動力設備拆裝實操培訓的重難點，也為船員適任證書考試中關于船舶動力設備拆裝項目的智能評估系統評分賦值提供依據。

參考文獻：

[1]王昊， 曾鴻， 倪文利， 等. 基于虛擬現實的船舶輔機設備拆裝訓練系統[J]. 江蘇科技大學學報（自然科學版）， 2017， 31（1）： 44-48.

[2]曾鴻， 王心紅， 張均東， 等. 面向實操評估的輪機虛擬拆裝考試系統開發[J]. 中國航海， 2014， 37（1）： 24-28.

[3]胡畔. 基于SolidWorks的虛擬設備拆裝系統研究[J]. 軟件導刊， 2011， 10（10）： 40-41.

[4]蘇玉龍， 吳桂濤， 曾鴻. 內河船機電設備虛擬拆裝考試系統設計與實現[J]. 大連海事大學學報， 2014， 40（2）： 101-104， 108. DOI： 10.16411/j.cnki.issn1006-7736.2014.02.023.

[5]侯政良， 張波， 劉敬. 基于VB的船舶柴油機虛擬拆裝系統研究[J]. 中國水運， 2013， 13（1）： 79-80.

[6]段尊雷， 任光， 曹輝， 等. 基于遺傳算法優化的虛擬機艙協作智能評估[J]. 哈爾濱工程大學學報， 2017， 38（ 4）： 514-520.

[7]張青， 鄭巖， 郭慶， 等. 航空發動機設備拆裝快速裝配仿真研究[J]. 計算機仿真， 2018， 35（3）： 257-261.

[8]ABUZIEDH ， SENBEL H ， AWAD M ，et al.A review of advances in design for disassembly with active disassembly applications[J]. Engineering Science and Technology， an International Journal， 2020， 23： 618-624. DOI： 10.1016/j.jestch.2019.07.003 2215-0986.

[9]BEDEOUIA， HADJ R B， HAMMADI M，et al. Assembly sequence plan generation of heavy machines based on the stability criterion[J]. The International Journal of Advanced Manufacturing Technology， 2019， 102： 2745-2755. DOI： 10.1007/s00170-019-03359-0.

[10]BATTAAO， DOIGUI A， HERAGU S S，et al. Design for manufacturing and assembly/disassembly： joint design of products and production systems[J]. International Journal of Production Research， 2018， 56（24）： 7181-7189. DOI： 10.1080/00207543.2018.1549795.

[11]KIMH J， HARMS R， GNTHER G.et al.Automatic control sequence generation for a hybrid disassembly system[J]. IEEE Transactions on Automation Science and Engineering， 2007， 4（2）： 194-205. DOI： 10.1109/TASE.2006.880538.

[12]MADARN， KALISKY T， COHEN R，et al. Immunization and epidemic dynamics in complex networks[J]. European Physical Journal B， 2004， 38（2）： 269-276. DOI： 10.1140/epjb/e2004-00119-8.

[13]MEYERSL A， POURBOHLOUL B， NEWMAN M E J，et al. Network theory and SARS： predicting outbreak diversity[J]. Journal of Theoretical Biology， 2005， 232（1）： 71-81. DOI： 10.1016/j.jtbi.2004.07.026.

[14]WANGYuhong， CULLINANE K. Measuring container port accessibility： an application of the principal eigenvector method （PEM）[J]. Maritime Economics & Logistics， 2008， 10（1/2）： 75-89.

[15]FREEMANL. Centrality in social networks conceptual clarification[J]. Social Networks， 1979， 1（3）： 215-239. DOI： 10.1016/0378-8733（78）90021-7.

（編輯 趙勉）