爆炸載荷下雙向梯度仿生夾芯圓板的力學行為*

王海任，李世強，劉志芳，雷建銀，李志強，王志華

（太原理工大學機械與運載工程學院應用力學研究所， 山西 太原 030024）

仿生結構代表了自然界千萬年選擇后的最優設計方案，如骨骼、貝殼、樹干、竹子、珊瑚、蜂窩等仿生結構[1-2]，包含各種梯度結構、分層結構、層狀結構、螺旋結構、多孔結構以及自組裝結構等。其中多孔結構擁有優異的吸能特性，因而被越來越多的研究者所關注[3-5]，常被作為吸能緩沖芯層應用于夾芯復合結構中。近年來，具有仿生多孔芯層的夾芯復合結構，因為有更好的比強度和較高的比剛度，被廣泛應用于現代航空航天、汽車工業、軍民安全防護等領域。隨著防護等級的提升以及減重要求的提高，對原有的仿生夾芯復合結構提出了更高的要求，即更好的防護性能與更輕的重量。夾芯結構梯度設計成為實現這一要求的新途徑，研究表明，分層梯度對提高夾芯結構強度、減輕結構重量更加有效[6]。

芯層的梯度可以通過改變胞元的壁厚[7]、改變胞元的大小[8-9]、改變胞元的組成材料[10-11]等方式獲得。2-D 多胞結構（如蜂窩結構）具有面外梯度和面內梯度兩個密度梯度方向。梯度夾芯結構的力學性能逐漸成為當前研究的熱點。研究內容主要包括面外梯度夾芯板（芯層的密度梯度方向與載荷加載方向一致）與面內梯度夾芯板（芯層的密度梯度方向與載荷加載方向垂直）的力學性能。Yang 等[12]基于非線性塑性波理論，提出了梯度多孔材料的最佳設計策略。Liang 等[13]利用理論和數值模擬方法，研究了相同質量下連續密度梯度多孔桿的爆炸響應和能量吸收特性。于渤等[14]首次引入芯層的面內梯度概念，提出了面內梯度夾芯的拓撲設計結構?，F有研究表明，面內梯度芯層同樣可以提高夾芯結構的性能。Yu 等[15]對面內梯度與均勻四邊形蜂窩夾芯板的動靜態力學行為進行了研究，發現通過引入面內梯度的方法，可以有效降低受爆炸載荷作用的夾芯板后面板撓度。Tao 等[16]研究發現，改變蜂窩“Y”形單胞沿長度方向的壁厚梯度，可以提高結構的能量吸收能力。Wang 等[17]根據王蓮仿生結構，設計了一種面內梯度芯層，發現引入面內梯度會降低夾芯板的后板撓度，提高夾芯板的抗爆性能。以上研究是對芯層單一方向梯度的改進，由于自然界中的結構大多具有多個方向梯度，因此研究具有多個方向梯度的夾芯結構具有重要意義。

本文中，基于一種王蓮仿生芯層結構，通過改變結構不同部位的壁厚來引入面內梯度與面外梯度，設計具有雙向梯度的夾芯圓板；運用ABAQUS 有限元模擬方法，分析雙向梯度夾芯圓板在爆炸載荷作用下的動態響應，重點研究不同爆炸載荷作用下雙向梯度夾芯圓板的后面板撓度、結構的變形模式、芯層的能量吸收等特性，并對梯度芯層的設計策略進行探討。

1 王蓮葉脈模型

與普通植物的葉脈相比，王蓮的葉面較寬、網狀葉脈寬大且較厚，其背面葉脈分布如圖1(a)所示。蜂窩狀結構由葉脈相交形成，葉脈的厚度和蜂窩狀結構的尺寸從中心到邊緣逐漸變化。粗壯的徑向葉脈與較薄的環形葉脈縱橫呈環形交錯，構成既美觀又能承重的整體。對王蓮葉脈的測量和分析表明，王蓮葉脈的分布符合Rudwig 植物形態學規律。為了將天然王蓮葉脈結構與相應的有限元模型緊密地聯系起來，在簡化模型中，王蓮葉脈結構中的徑向葉脈和環形葉脈分別用放射狀的徑向網和環形網表示。圖1(b)為仿生王蓮葉脈拓撲演化模型，模型中的尺寸關系為：OA=15 mm，OB=40 mm，OC=65 mm，OD=85 mm，OE=100 mm，各部分的長度比例滿足黃金分割率[18]。

圖1 芯層設計策略Fig.1 Core design strategy

2 有限元模型

2.1 芯層有限元模型的建立

采用有限元軟件ABAQUS/Explicit 建立了以圖1(c)為基礎的夾芯圓板有限元模型，如圖2所示。夾芯圓板的半徑（R）為100 mm。前面板厚度（δf）和后面板厚度（δb）均為1 mm，芯層高度（hC）為21 mm。芯層沿高度方向分為3 層，每層高度為7 mm，分別用C1、C2、C3 層表示。夾芯圓板的邊界條件設置為環向固支約束。芯層和面板使用S4R 殼單元進行網格劃分，網格尺寸為1 mm。單元類型為有限薄膜應變，動態縮減積分。接觸設置為通用接觸，用于避免前后面板與芯層發生穿透。分析過程采用動態顯式算法。TNT 炸藥質量采用15、25、35 g，爆炸距離為200 mm。根據KNR 理論，可以計算考慮流固耦合作用時前面板的爆炸沖量，作用于前面板的壓力形式設置為[19]：

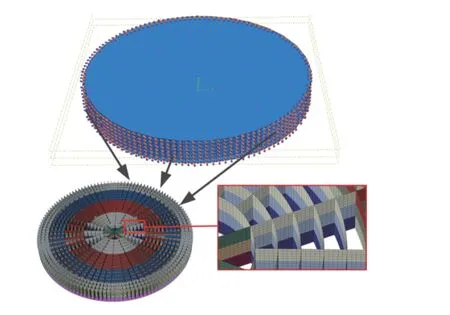
圖2 有限元模型的網格劃分Fig.2 Adopted mesh of the FE model

式中：p 為壓力；pr為反射超壓峰值，設置為6.32、9.13、11.80 MPa；tr為反射波作用時間，設置為0.055 48、0.053 54、0.052 20 ms。

在ABAQUS 有限元軟件中，將此載荷采用壓力-時間曲線的形式作用于前面板來模擬爆炸載荷。

為了確定網格大小并保證計算精度，首先進行網格收斂性驗證。選取網格尺寸分別為2.0、1.0 和0.8 mm 的3 個模型進行模擬，芯層單元數量分別為62 892、219 240、349 704。炸藥質量為25 g，3 個模型的后面板撓度歷史如圖3(a)所示。

經過綜合比較后面板撓度計算精度與計算時間，采用1.0 mm 的網格進行后續計算。由于采用的殼單元使用了縮減積分，必須進行沙漏控制。圖3(b)給出了1.0 mm 模型的能量歷史曲線，從圖3(b)中可以看出，偽應變能Ea占總能量的3%，說明網格劃分合理，而外力做功Ew等于系統的內能Ei與系統動能Ek之和，說明所建立的模型符合計算要求。

圖3 有限元模擬有效性驗證Fig.3 Verification of finite element simulation

通過改變殼單元的厚度，可以得到不同密度梯度的芯層結構。在接下來的有限元模擬中，通過改變S4R 殼單元的壁厚來獲得不同梯度的模型，而不需要改變模型的基本構型，由此可以避免因重復建模產生的計算誤差。

2.2 材料參數

前后面板材料選取5052 鋁合金[20]，仿生芯層基體材料采用6060T4 鋁合金[21]。本構關系采用雙線性本構模型：

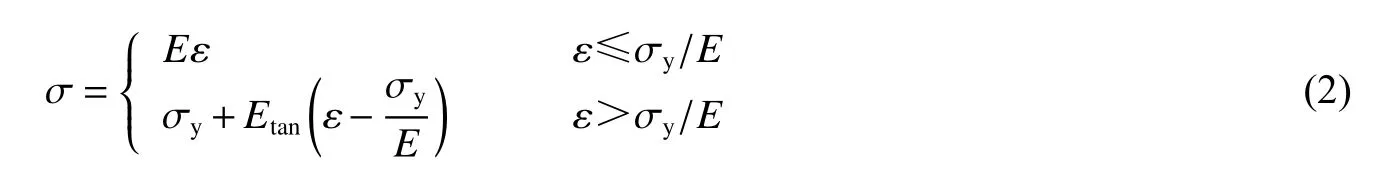
式中：σ 為應力，ε 為應變，E 為彈性模量，v 為泊松比，σy為屈服強度，Etan為切線模量。具體的材料參數如表1 所示，其中ρ 為密度。由于兩種鋁合金材料的應變率敏感性相對較弱，在模擬中沒有考慮應變率敏感性。

相對密度是格柵類材料的重要參數。按照芯層的徑向脈絡分岔部位劃分為5 部分，如圖1(b)和(c)所示，不同部分相對密度的計算公式為：

表1 鋁合金的材料參數Table 1 Material parameters of aluminum alloy

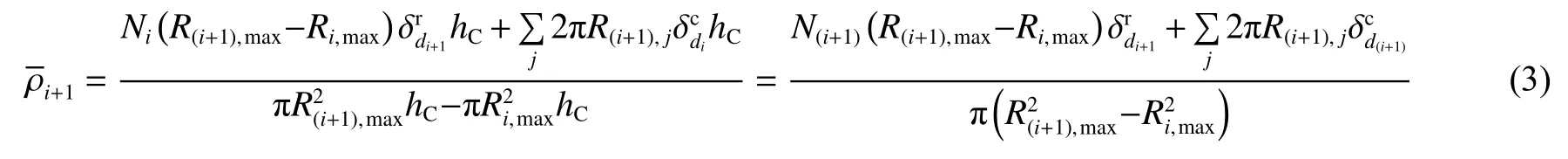
表2 列出了8 種類型的芯層，其中面內梯度包括面內負梯度（面內梯度從圓心到邊界單調遞增）、面內混合梯度（面內梯度先降低再增高）、面內正梯度（面內梯度單調遞減）與均勻芯層4 種，并分別與面外正梯度和面外負梯度進行耦合。由于芯層面外方向具有3 層，選取芯層中間層C2 作為代表，列舉面內各部分壁厚信息。對于面外方向，面外負梯度模型的C1 芯層壁厚為C2 芯層壁厚的2/3，C3 芯層壁厚為C2 芯層壁厚的4/3，而面外正梯度模型的梯度芯層排列順序則正好相反。命名規則為：k=0.8- Ⅰ表示從圓心向邊界處，面內5 部分中相鄰兩部分的壁厚比為0.8，即面內負梯度，Ⅰ表示從前面板到后面板，芯層的相對密度逐漸增加，即面外負梯度；k=0.8- Ⅱ表示面內為負梯度，Ⅱ表示從前面板到后面板，芯層的相對密度逐漸降低，即面外正梯度；k=1.2，k=1.6 分別表示面內混合梯度和面內正梯度；UG- Ⅰ表示芯層面內梯度均勻，面外負梯度；UG- Ⅱ表示芯層面內梯度均勻，面外正梯度。

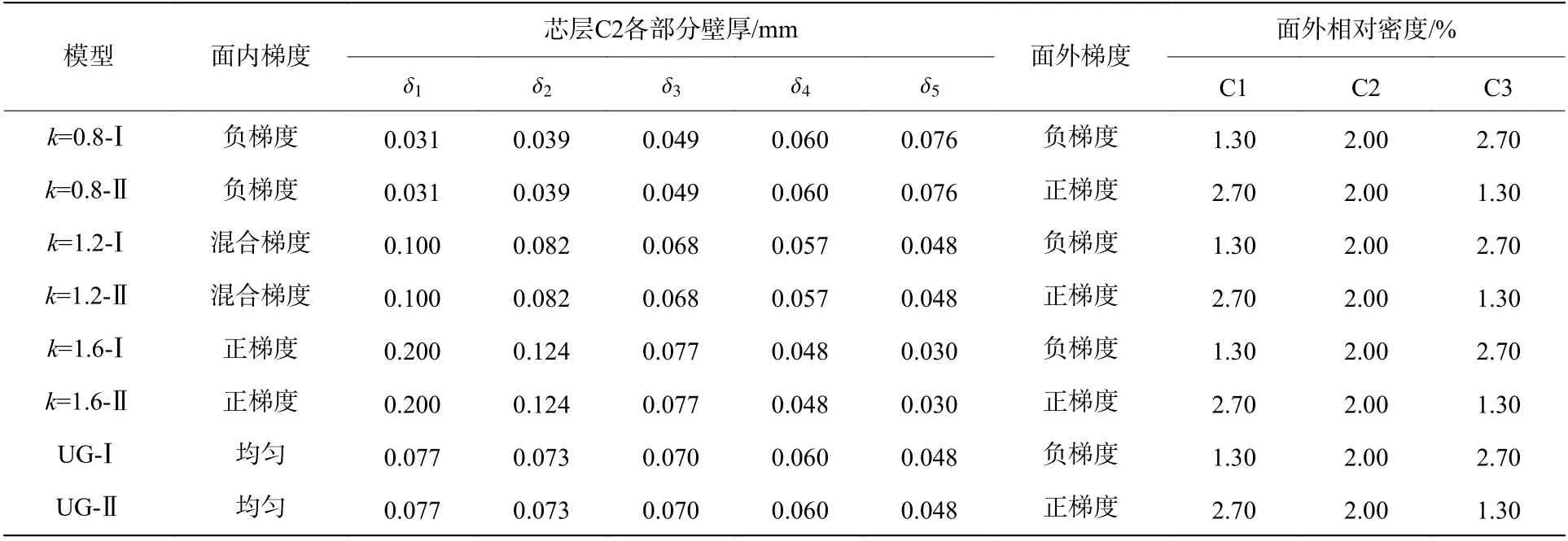
表2 模型類型與相關參數Table 2 Model type and related parameters

根據式(3)與表2，可以計算得到各部分的相對密度，表3 顯示了C2 芯層平均相對密度為2.00%時，不同面內梯度芯層各部分的相對密度，不同面內梯度芯層的總質量相同，但是各部分的相對密度存在差異。

表3 C2 面內梯度模型各部分相對密度Table 3 Relative density of in-plane gradient model C2

3 結果分析

對8 種密度梯度夾芯結構有限元模型在炸藥質量分別為15、25、35 g 時的3 種工況進行模擬。將得到的數值模擬結果進行參數化分析，討論不同梯度夾層結構在爆炸載荷作用下的響應。分別從夾芯圓板的前后面板撓度、芯層壓縮量、變形模式和能量吸收能力等方面進行分析[6]，并探討爆炸載荷作用下的夾芯圓板芯層的設計策略。

3.1 后面板的撓度

圖4 不同爆炸載荷下不同密度梯度夾芯板后面板的最大撓度Fig.4 Deflection of the back panel of the sandwich panel with different density gradients under various blast loadings

8 種梯度夾芯圓板在不同爆炸載荷作用下的后面板撓度如圖4 所示。由圖4 可以看出，不同梯度夾芯圓板后面板的撓度差別較大。最大撓度與最小撓度相差30%～40%，并且差異隨著爆炸載荷的增加而增大。

通過對比單一面外梯度夾芯圓板的后面板撓度，可以看出：在研究載荷范圍內，Ⅰ型夾芯圓板的抗變形能力略優于Ⅱ型夾芯圓板。當與面內梯度結合之后，Ⅰ型夾芯圓板中的k=1.2- Ⅰ型夾芯圓板后面板撓度進一步降低20%～25%，而k=1.6- Ⅱ型夾芯圓板具有最大的后面板撓度。雖然沒有改變Ⅰ型面外梯度夾芯圓板優于Ⅱ型夾芯圓板的規律，但是根據文獻[17]，在此爆炸載荷范圍內，面內梯度夾芯圓板后面板撓度規律為 γk=0.8＜γk=1.2＜γk=1.6，即面內梯度k=0.8 具有最小的后面板撓度。當兩種梯度耦合時，k=0.8 與模式Ⅰ的組合k=0.8- Ⅰ并沒有表現出最佳的抗變形能力，兩種梯度結合后，變形模式的改變導致抗變形能力被削弱。而面內梯度較差的k=1.6 與面外梯度較差的模式Ⅱ相結合后，k=1.6- Ⅱ抗變形能力進一步變差。面內混合梯度k=1.2 與面外梯度Ⅰ結合卻表現出了最好的抗變形能力，表明這兩種密度梯度的結合會提高芯層的能量吸收能力，從而增強其抗變形能力。而面內混合梯度k=1.2 與面外梯度Ⅱ相結合后，夾芯圓板的抗變形能力弱于有k=1.2- Ⅰ ，表明雖然引入面內梯度可以提高芯層的抗變形能力，但此時面外梯度對結構抗變形能力的影響仍然占據主導地位。為了進一步研究面內梯度與面外梯度的耦合行為，對k=1.2 的兩種梯度模型的前后面板撓度曲線進行了研究。

圖5 為k=1.2 的兩種雙向梯度夾芯圓板的前后面板撓度-時間曲線。通過觀察前后面板撓度的差值，可以發現此差值呈現出較明顯的夾芯結構三階段變形模式。階段Ⅰ（t=0～0.052 ms）表示載荷作用階段，即流固耦合階段，這一階段載荷作用于前面板，前面板受到爆炸載荷沖量的作用開始運動。階段Ⅱ（t=0.052～0.200 ms）表示芯層的壓縮階段，通過觀察前后面板撓度的差值，可以發現芯層壓縮大約在0.200 ms 時停止，隨后進入階段Ⅲ（t=0.200～0.400 ms）。階段Ⅲ表現為夾芯圓板的整體大變形。首先前后面板以相同速度運動，直到塑性鉸環從初始位置移動到圓板中心（Phase Ⅰ ）；隨后夾芯圓板開始減速運動，當圓板中心速度為零時（Phase Ⅱ ），后面板達到最大撓度；最后夾芯圓板在平衡位置震蕩運動。通過對比兩種夾芯結構的前后面板撓度曲線可以發現，k=1.2- Ⅱ在階段Ⅱ圓板中心處芯層的壓縮應變約為25%，低于k=1.2- Ⅰ的38%。同時，k=1.2- Ⅱ進入階段Ⅲ的時間早于前者，前后面板共同運動的時間延長，這是引起后面板撓度增加的原因之一。

圖5 k=1.2 的兩種不同面外梯度芯層在炸藥為25 g 時的前后面板撓度曲線Fig.5 Deflections of front and back panels with two different out-of-plane gradient cores with k=1.2 when the explosive mass is 25 g

3.2 變形模式

圖6 表示k=1.2 的兩種雙向梯度夾芯圓板在TNT 炸藥為25 g、芯層壓縮階段結束時的變形模態。對于Ⅰ型結構，芯層壓縮屬于漸進壓縮模式，芯層順著載荷方向逐層壓縮；而對于Ⅱ型模式，芯層下方壓縮量明顯增大，并且由于引入了面內梯度，面內不同部位的壓縮率也各不相同。k=1.2- Ⅰ型夾芯圓板的Part 1、Part 2、Part 3 上部分壓縮明顯，下部分壓縮不明顯；k=1.2- Ⅱ型夾芯圓板的Part 1 與Part 2 下部分壓縮明顯，上部分壓縮不明顯，而Part 3 上部分壓縮明顯，下部分壓縮不明顯。因此針對此情況，可以對Part 1 與Part 2 進行結構優化，降低C3 層Part 1 與Part 2 的相對密度，進一步提高梯度芯層中間部位的能量吸收。C3 層的Part 3 基本沒有被壓縮，因而可以適當降低其相對密度從而減輕芯層的質量。

圖6 k=1.2 時兩種夾芯板的變形模式Fig.6 Deformation mode diagram of two kinds of sandwich plates with k=1.2

3.3 能量吸收能力

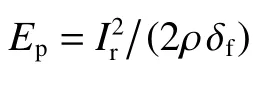
與單一面外梯度設計策略相比，面內梯度與面外梯度相結合的芯層設計策略的能量吸收能力進一步提高了20%～30%。

將環向邊界設定為自由邊界，增加自由邊界的梯度夾芯圓板在炸藥質量為25 g 時的芯層能量吸收對照結果，如圖8 所示。

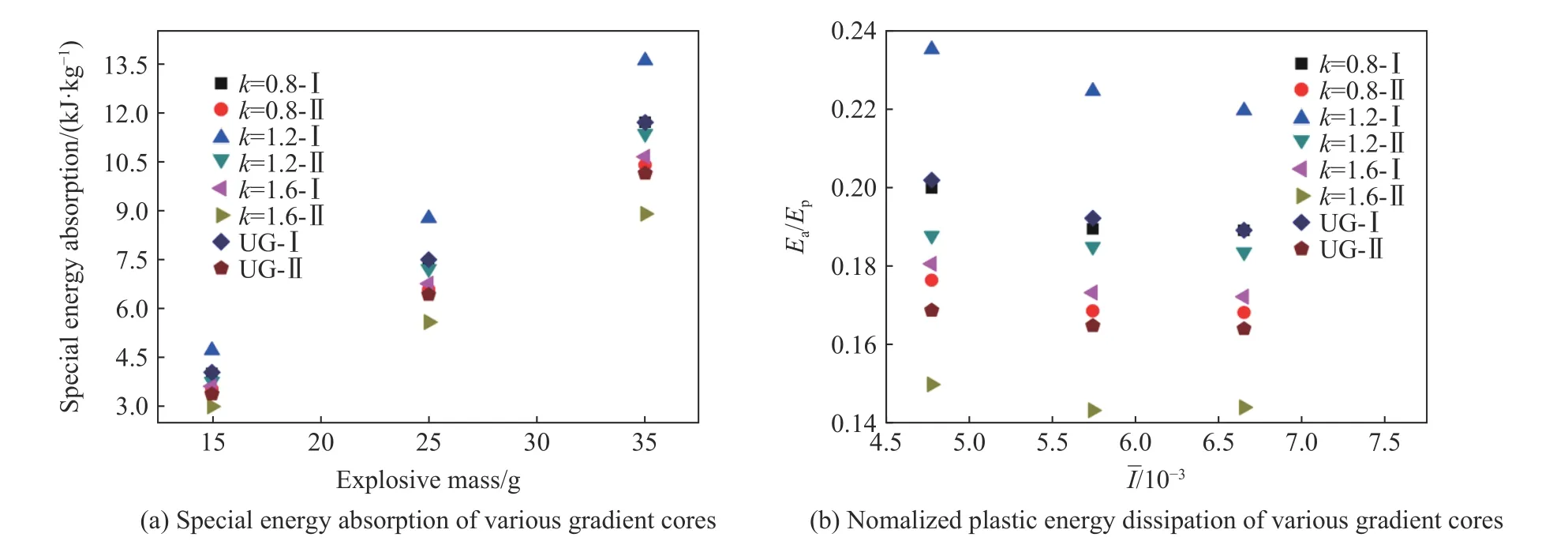
圖7 不同梯度芯層能量吸收比較Fig.7 Comparisons of energy absorption of different gradient cores

圖8 自由邊界的梯度夾芯圓板在炸藥質量為25 g 時芯層能量吸收Fig.8 Energy absorption of graded sandwich circular plate with free boundary when explosive mass is 25 g

從圖8 可以看出：當邊界自由、炸藥質量為25 g 時，面外梯度Ⅰ型結構C1、C2 與C3 層的能量吸收依次降低，而面外梯度Ⅱ型結構C1、C2 與C3 層的能量吸收較均衡。總體而言，面外梯度Ⅱ型結構的總能量吸收低于Ⅰ型結構。兩種梯度耦合時，相較于本文中給出的其他雙向梯度芯層，k=1.2- Ⅰ型芯層結構具有最好的能量吸收能力。

3.4 芯層設計策略探討

夾芯結構的抗爆性能，很大程度上依賴于芯層的性能，而芯層的性能不僅與組成材料的性能有關，也與其微觀結構有關。受自然界的啟發，大量輕質高強的芯層被設計制造出來。在均勻芯層中引入面外梯度，可以極大地提高芯層的性能。近期也有研究表明，將面內梯度引入均勻芯層也可以有效提高芯層的性能[14-17]。本文中，將兩種梯度結合，將面內梯度引入到面外梯度芯層中，設計了一種雙向梯度夾芯結構，并對不同雙向梯度夾芯結構在爆炸載荷作用下的性能進行了研究。結合后面板跨中撓度和芯層能量吸收能力，發現在本文中給定的載荷范圍與模型范圍內，面外梯度夾芯結構中采用面內梯度先減小后增大，面外梯度從前到后逐漸增大的模式可以有效提高芯層的能量吸收能力，并降低后面板的撓度。對本文得到的最佳芯層排列模式（k=1.2- Ⅰ ）的變形情況進行分析，可以看出：此類雙梯度模型在受到爆炸載荷作用時，仍存在部分區域未發生明顯的變形，需要更進一步優化。因此，梯度芯層設計需要綜合考慮結構單胞的幾何尺寸、芯層的排列順序以及爆炸載荷的強度等因素，并根據實際情況進行合理設計。

4 結 論

基于一種王蓮仿生芯層結構，通過改變結構不同部位壁厚的方式引入面內梯度和面外梯度，設計了不同面內梯度與面外梯度耦合的雙向梯度芯層夾芯圓板，利用ABAQUS 有限元模擬分析了雙向梯度夾芯圓板在爆炸載荷作用下的動態響應，得到的主要結論如下：

（1）在芯層質量相同時，相較于單一面外梯度夾芯圓板，合理的雙向梯度設計可以在不額外增加芯層質量的前提下，將夾芯圓板的后面板撓度降低20%～25%，從而提高夾芯結構的抗爆性能。

（2）TNT 炸藥質量分別為15、25、35 g，爆炸距離為200 mm 加載條件下的固支夾芯圓板，面內梯度先減小后增大，面外梯度從前到后逐漸增大的芯層排列模式可以有效提高芯層的總能量吸收，能量吸收能力比單一面外梯度夾芯圓板提高了20%～30%，隨著載荷的增加，總吸能逐漸增大。將載荷與吸能進行無量綱化處理后，發現芯層的能量吸收效率隨載荷的增加而逐漸降低。

（3）從結構的變形模式來看，目前芯層結構仍可進一步優化，通過優化芯層各部分壁厚的分布，實現降低芯層質量的同時提高芯層的能量吸收能力。

（4）梯度芯層設計受到結構單胞的幾何尺寸、芯層的排列順序以及爆炸荷載強度等因素的影響，需要根據實際情況來合理設計。

感謝中國科學院西雙版納熱帶植物園園林園藝部吳福川副部長提供的王蓮高清圖片，并開展了有益的討論。