含橡膠連桿平行四邊形機構的非線性動力學分析
程壽國 ,劉 毅 ,蘇春芳 ,劉洪斌
(1.上海大學 機電工程與自動化學院,上海 200072;2.江陰職業技術學院 a.機電工程系,b.計算機科學系,江蘇 江陰 214405;3.國家電網湖北省電力有限公司 五峰縣供電公司,湖北 宜昌 443413)
0 引言
橡膠材料的阻尼特性和非線性特性研究已經引起了許多學者的關注.Balasubramanian 等[1]研究了橡膠矩形板阻尼與三種不同耗散模型的關系,并用激光多普勒測振儀進行了驗證.Menga 等[2]討論了幾何參數和材料參數對橡膠層滾動軸承動態特性的影響,他們發現周期性和非周期性動力學響應同時存在.Gong等[3]研究了車身低頻模態的平順性和振動能量對橡膠元件環境溫度降低的影響.為了保證車輛在一定速度下具有良好的乘坐舒適性,他們提出了橡膠部件工作的合理環境溫度范圍.Luo[4]和Shi[5]還研究了橡膠彈簧模型的非線性動力學在車輛動力學中的應用.Xiao等[6-8]提出了往復壓縮機出現故障時的非線性動力學問題,他們研究了平動關節的間隙、旋轉關節的間隙和考慮活塞桿為柔性桿時多種情況下的非線性動力學行為.Zhao等[9]介紹了往復式壓縮機平面間隙剛柔耦合動力學的仿真與優化問題.
以上學者主要研究了橡膠件的靜力學問題和剛性桿機構運動中的非線性動力學問題.本文主要分析帶有橡膠連桿的平行四邊形機構的動力學行為,并用有限元法對其進行剛柔耦合分析,為含橡膠構件的動力學研究和含大變形構件的非線性研究提供參考.
1 含橡膠連桿的平行四邊形機構簡介
圖1 為平行四邊形機構示意圖.曲柄OA 是一個驅動曲柄,它以恒定速度旋轉.連桿AB 的材料為橡膠,BC桿為從動曲柄.驅動曲柄OA的長度與從動曲柄BC的長度相同.連桿AB的長度與機架桿OC的長度相同.當OA,AB,BC 和OC 均為剛性桿時,則OA 和BC 的轉速完全相同,即輸入轉速和輸出轉速相同.當桿AB為橡膠材料時,橡膠材料的特性使得桿AB往往不能被認為是一個剛性桿.在桿OA的驅動下,連桿AB 將發生較大的變形和彎曲,使得桿BC 的動力特性比全剛體時復雜得多.圖2 為橡膠連桿AB 的尺寸圖.連桿AB的有效長度為220 mm,連桿厚度為10 mm,呈細長孔狀(延長孔).在桿AB兩側的半圓中心分別開一個直徑為15 mm 的軸承孔,兩個軸承孔與各自相連的兩個曲柄軸承孔平面鉸連接.曲柄OA 和曲柄BC的形狀相似,旋轉鉸中心的距離為100 mm.
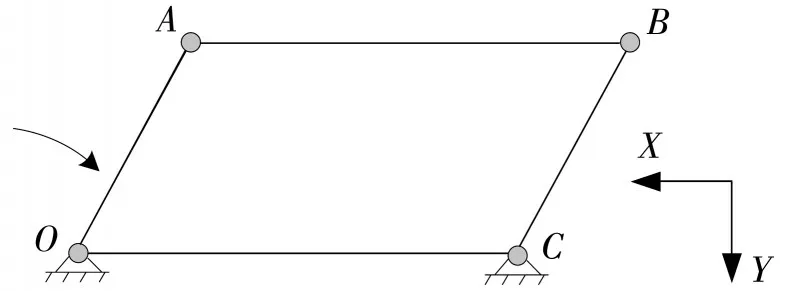
圖1 平行四邊形機構示意圖
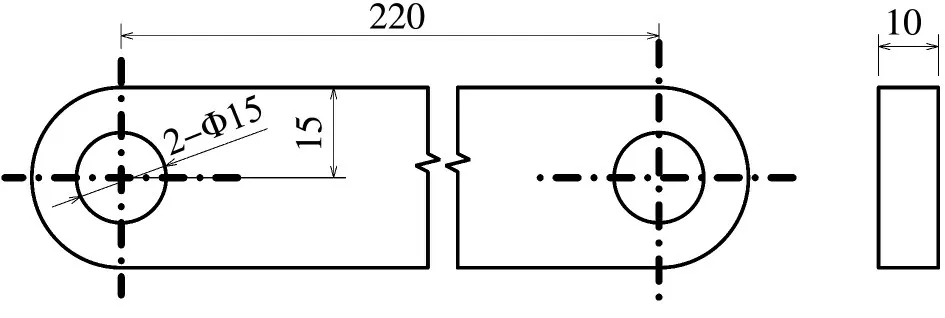
圖2 橡膠連桿AB的尺寸圖
2 含橡膠連桿的平行四邊形機構動力學分析
為了研究橡膠連桿的材料特性,本文采用有限元法將橡膠連桿生成了柔性體.利用SimDesigner 軟件調用MSC-Nastran 求解器計算橡膠連桿的大變形,并在動態仿真前將連桿作為柔性體激活.通過軟件仿真,可以一次計算出許多動態參數.本文以從動曲柄的Y 方向位移、速度、加速度和角速度為研究對象,圖3為主動曲柄轉速為75 r/min時橡膠連桿平行四邊形機構從動曲柄的動力學響應時域圖.
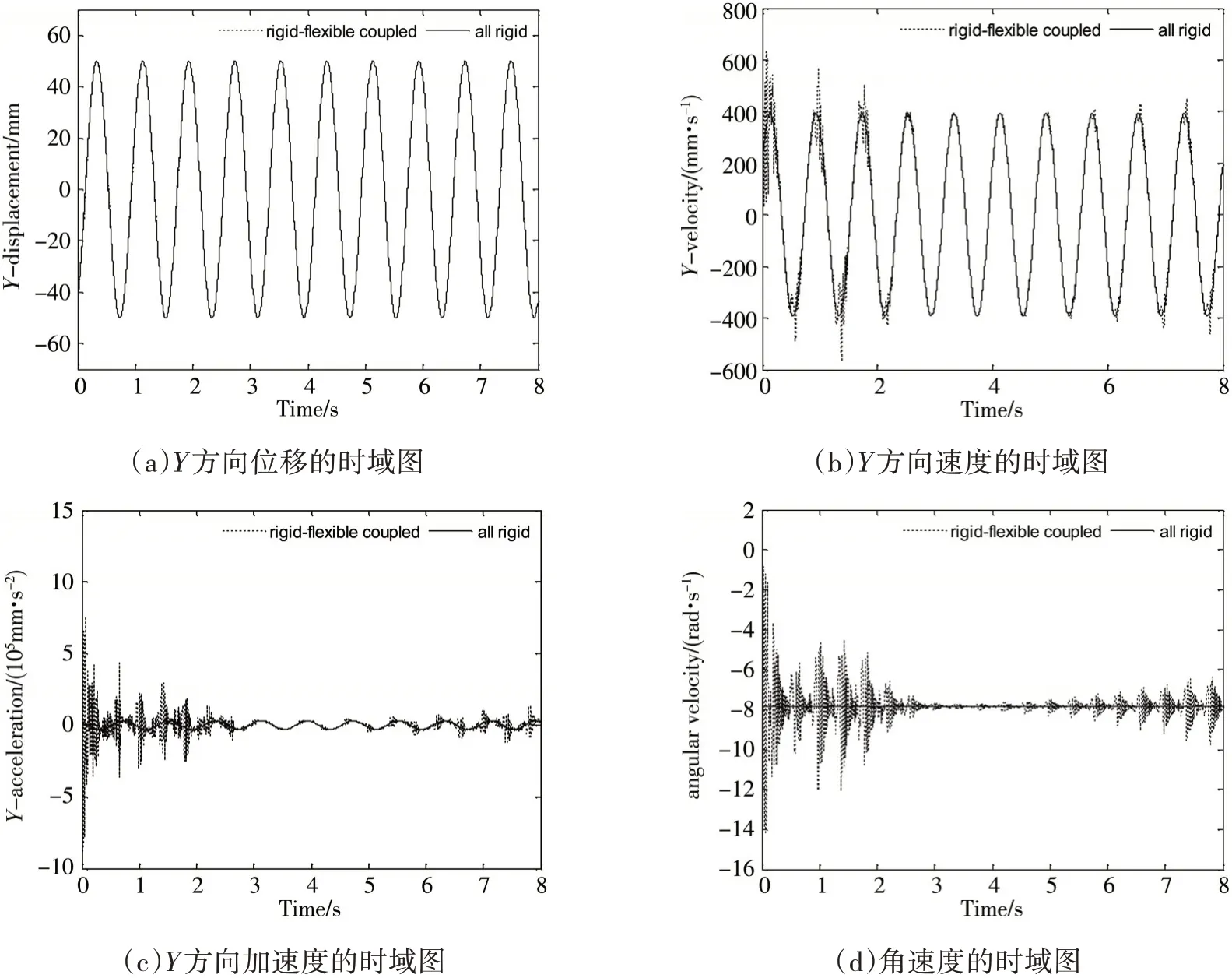
圖3 主動曲柄轉速為75 r/min時橡膠連桿平行四邊形機構從動曲柄的動力學響應時域圖
從圖3(a)可以看出,剛柔耦合系統與全剛體平行四邊形系統的位移曲線幾乎重合,說明橡膠桿材料柔性對Y方向位移的影響不大.
從圖3(b)可以看出,剛柔耦合系統與全剛體平行四邊形系統的速度曲線相比較在上下頂點處有一些波動,波動約在三個周期(每個周期0.8 s)左右消失,大約從第七個周期開始逐漸增強,這也反映了橡膠材料的阻尼特性.從速度-時間動力響應時域圖可以看出,波動逐漸減小,經過一段時間后逐漸增大.
圖3(c)是全剛體系統和剛柔耦合系統在Y方向加速度的時域圖.在剛柔耦合系統中,加速度約在前三個周期時間內的波動非常明顯,遠大于圖3(a)和圖3(b)中的波動.研究還表明,加速度對橡膠材料的特性非常敏感,變化劇烈.從圖中還可以看出,前三個周期變化較大,然后波動變化逐漸減小.在曲柄轉動3~5 s時間內,變化不大,與速度的時域圖狀態相似.可以近似地認為,前3 s的加速度變化是非周期性的,3~5 s是周期性的,5 s后的非周期性信號和波動變化是逐漸增強的.
圖3(d)是角速度的時域圖.圖中實線為全剛體(7.853 rad/s)系統從動曲柄的角速度.角速度時域圖與加速度時域圖在Y 方向的變化趨勢相似.轉動開始時,波動較大,約3 s后開始減小,3~5 s接近周期性信號,5 s后波動逐漸增大.
3 系統的穩定性判別
3.1 相圖觀測法
相圖觀測法是判斷系統運動穩定性最直接的方法之一.如果系統在多個運動周期中的相圖是同一條閉合曲線,則可以認為系統是周期性運動.如果相圖是一條多周期、無重復的曲線,則系統運動可視為非周期性運動.它是否是混沌運動,還需要用其他判據進一步分析.圖4為從動曲柄的運動響應相圖.
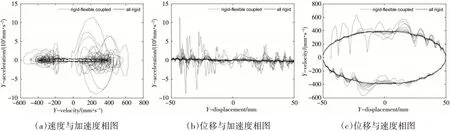
圖4 從動曲柄的運動響應相圖
圖4 (a)是從動曲柄中心點Y 方向速度和加速度的相圖.全剛體系統的速度和加速度的相圖是非常平坦的橢圓形狀,剛柔耦合系統的位移和加速度相圖變化劇烈.
圖4(b)是從動曲柄中心點Y 方向位移和加速度的相圖.全剛體系統的位移和加速度相圖近似于一條100 mm長的 “線段” ,剛柔耦合系統的位移和加速度相圖圍繞這條線段跳躍并劇烈變化.
圖4(c)是從動曲柄中心點Y 方向位移和速度的相圖,與前兩個相圖相比,相圖清晰得多.從圖中可以看出,帶有橡膠連桿的從動曲柄的運動是混沌的.
3.2 計算最大Lyapunov指數的判別法
計算最大Lyapunov 指數是判斷系統是否混沌的定性方法之一.如果計算得到的系統最大Lyapunov指數大于零,通常可以用來判斷系統的運動是混沌的.
將從動曲柄Y方向加速度仿真計算的數據導出到MATLAB軟件中,通過WOLF方法計算最大Lyapunov指數.圖5 為當曲柄轉速為75 r/min 時的Lyapunov 譜,求得的最大Lyapunov 指數為0.018.圖6 為當曲柄轉速為60,90,120 r/min時,求得的最大Lyapunov指數分別為0.024 6,0.067 6和0.063 3.
在上述四種速度下計算得到的最大Lyapunov指數均為正數,可以判斷從動曲柄的運動是混沌的.
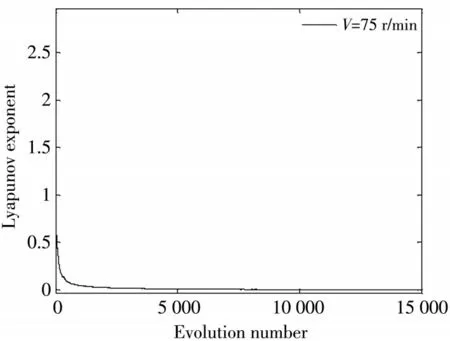
圖5 轉速為75 r/min時的Lyapunov指數
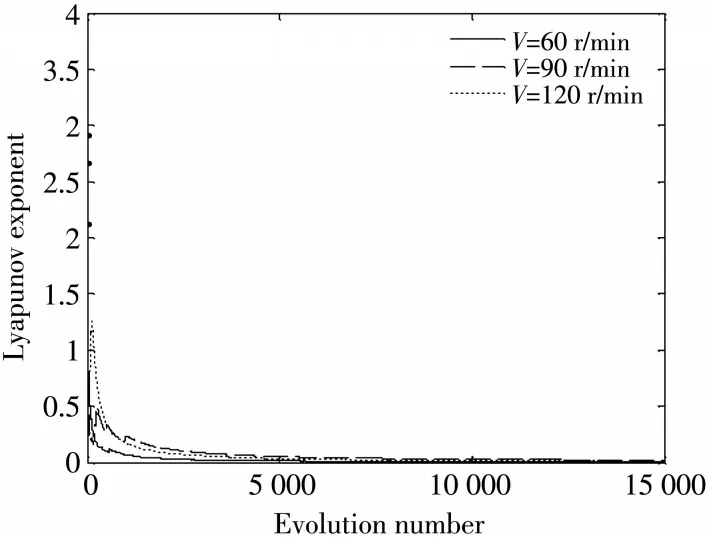
圖6 轉速為60,90,120 r/min時的Lyapunov指數
4 結論
本文采用有限元法對柔性體進行建模,并利用動力學仿真軟件對帶橡膠連桿的平行四邊形機構的動力學行為進行了計算.通過分析Y 方向加速度和從動曲柄角速度的時域圖,發現系統在運動時間上同時存在周期性運動和非周期性運動.利用相圖和最大Lyapunov 指數判斷系統中從動曲柄的運動是混沌的.

