亞聲速條件下十字形傘充滿時間系數的解算方法及仿真驗證

喻東明，馬嘯民，楊 品

（1.航空工業航宇救生裝備有限公司空降空投技術研發部,襄陽441003；2.航空工業航宇救生裝備有限公司應用技術部,襄陽441003）

在降落傘的工作過程中，充氣階段是最為復雜的一個階段，在該過程傘衣的結構變形和傘衣周圍的流場變化相互耦合，使得難以精確建立傘衣充氣的理論模型[1-3]。目前,對于降落傘充氣性能的研究主要是通過一些實驗結果的統計分析來獲取的,充氣性能與開傘條件之間的關系也是通過試驗結果統計、擬合出來的。這使得充氣時間、傘衣投影面積變化的一些經驗公式存在著一定的局限性[4]，只能在某型情況下適用。

十字形傘最早由法國人提出，具有工藝簡單、穩定性好、開傘動載小等優點，被廣泛應用于飛機阻力傘、航彈傘及投物傘領域。該傘的結構簡單，傘衣由兩個相同的矩形織物面組成，這兩個矩形織物面彼此成直角相交連接，形成一個有4 個相同矩形幅的平面，結構示意圖見圖1。

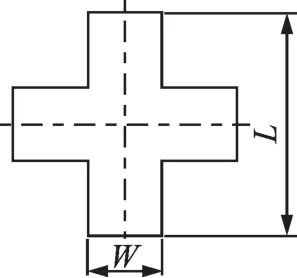
圖1 十字形傘示意圖Fig.1 Schematic diagram of cruciform parachute

十字形傘的充滿時間與開傘動載、充滿距離關系密切，特別是對于水平著陸的飛行器減速而言，充滿時間的長短則直接影響著滑跑距離消耗的多寡。因此，通過放傘速度以及傘衣面積評估十字形傘充滿時間對于研究飛行器著陸滑跑性能以及十字形傘開傘載荷特性具有極其重要的意義，在目前缺乏十字形傘充滿時間參數的條件下評估其充滿時間則需要進行充滿時間系數的解算以及驗證。

1 解算方法及結果

1.1 經驗公式的簡化

降落傘充氣過程是一個流進傘衣的空氣體積大于流出的空氣體積而使傘衣體積逐漸擴大的過程（圖2），傘衣內空氣的平衡方程如下

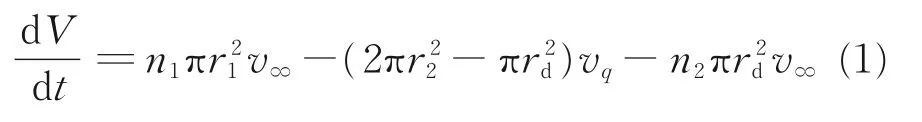
式中：V 為傘衣體積；rd為傘頂孔半徑；v∞、vq為自由氣流速度和透過傘衣織物的平均氣流速度；n1、n2為入口氣流和通過傘頂孔氣流速度修正系數。

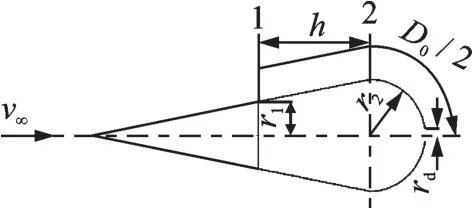
圖2 傘衣充氣模型Fig.2 Canopy inflation model

從以上平衡方程可以看出，傘衣體積V 越大則充滿時間越長，來流速度v∞越大則充滿時間越短。降落傘的充滿時間指傘衣拉直后從底邊充氣開始至傘衣完全張滿結束所經歷的過程時長。降落傘的充滿時間與拉直速度成反比，與其幾何結構尺寸成正比。降落傘充滿時間的經驗公式如下

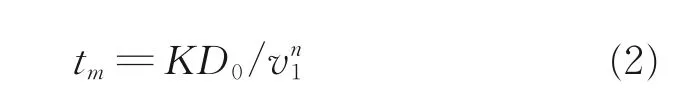
式中：v1為拉直速度；D0為傘衣名義面積；K 為傘衣充滿時間系數；為簡便起見，n 取1。

根據充氣過程中物-傘系統的減速程度，降落傘充氣分為“有限質量”充氣和“無限質量”充氣。“無限質量”充氣引起的物-傘系統減速可忽略不計，而“有限質量”充氣引起的物-傘系統減速則非常明顯。

由于“無限質量”充氣引起的物-傘系統減速可忽略不計，對于“無限質量”充氣、亞聲速工況下的十字形傘，其充滿時間的經驗公式則可簡化為（以開傘速度vf代替拉直速度v1）

1.2 解算過程及結果

目前缺乏十字形傘充滿時間系數K 的取值規范，難以事先評估不同傘衣面積十字形傘的充滿時間，制約著飛行器著陸滑跑性能以及十字形傘開傘載荷特性的研究。因此，需要結合充滿時間的實測值通過式（5）解算出充滿時間系數

根據定義，傘衣面積與傘衣名義直徑的關系如下

將充滿時間實測均值μ、開傘速度vf以及由式（5）計算出的名義直徑D0代入式（4），容易得出充滿時間系數K=9.47。

1.3 圓整處理

以上得出的充滿時間系數K 含有小數位，需要圓整后才便于其在工程上的推廣應用。

在充滿時間的實際判讀過程中，起始影像中難免會伴有部分傘衣、傘繩拉直的畫面，即充滿時間的判讀起點有時會前移，導致其實測值比真實結果偏大。鑒于此，充滿時間系數K 應向下圓整為9。

2 校驗對比

2005 年某型阻力傘（簡稱15 型）進行了飛機著陸放傘試驗，該型傘傘衣為十字形，面積20 m2，放傘速度（即下文中所稱開傘速度）一般為300 km/h（83.3 m/s），處于亞聲速階段。

試驗過程中利用高速攝像機拍攝了阻力傘放傘過程的影像，通過判讀傘衣從底邊充氣（圖3）開始至完全張滿（圖4）所經歷的影像幀數（每秒125 幀）換算得出的充滿時間的實測值如表1所示。

圖3 傘衣底邊充氣Fig.3 Inflation at the bottom of the canopy

圖4 傘衣完全張滿Fig.4 Inflated canopy

表1 阻力傘充氣時間實測值Table 1 Measured value of inflation time of drag para-chute

將充滿時間看作連續性隨機變量X，假設其服從正態分布，根據式（6，7）可以計算出以上4 個樣本的均值μ 為0.573，樣本標準差σ 為0.077，95%置信區間（0.419，0.727），數據離散程度不大。可以認為，該組小樣本量數據作為后續解算的依據是可信的。

根據相關文獻資料介紹，美國標準T-10 型傘兵傘為平面底邊延伸傘，與十字形傘在傘型分類上同屬于密實織物傘，其充滿時間系數K 通常取8。通過傘型比對可知：十字形傘充滿時間系數的解算結果稍大于已有的密實織物傘經驗值，這是因為十字形傘和平面底邊延伸傘雖同屬密實織物傘，但前者在傘衣張滿后葉片間會形成缺口，加大了流出空氣的體積，從而延緩了傘衣體積擴大的進程，導致充滿時間延長，充滿時間系數K 稍大。

15 型傘與T-10 型傘兵傘在相同開傘速度條件下的充滿時間明顯存在差異，這主要是因為兩者的名義直徑相差太大導致的（見表2），與十字形傘充滿時間系數的解算結果稍大于已有的密實織物傘取值結果的結論不矛盾。

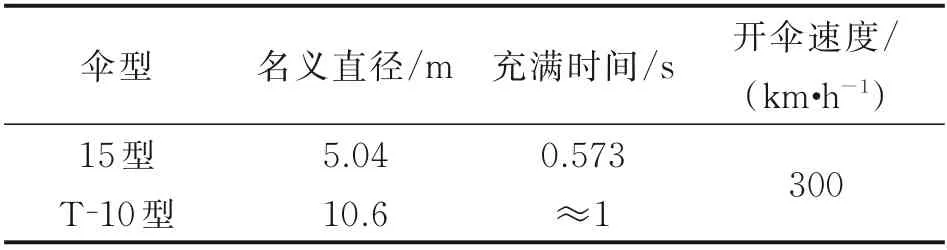
表2 T-10 型傘兵傘與15 型傘Table 2 T-10 paratrooper and 15 paratrooper

為了便于估計不同傘衣面積的十字形傘充滿時間，將式（5）變換為

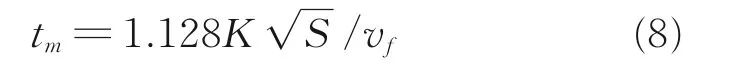
將開傘速度及K 值代入，式（8）可進一步簡化為

一定開傘速度（tm）條件下不同傘衣面積（S）的十字形傘充滿時間曲線如圖5 所示。

注：以上結果是在“無限質量”充氣條件下獲得的，對于“有限質量”充氣條件下十字形傘充滿時間的解算，需在開展進一步研究的基礎上對以上結果予以適當修正。

3 仿真驗證

前文通過利用小樣本量實測值解算十字形傘充滿時間系數的方法得到了相應結果，該結果是否準確、可信，除完成初步校驗外，還應進行一定范圍的仿真驗證。

以另一型別十字形阻力傘放傘為研究對象，建立仿真模型，模擬阻力傘從開始充氣至張滿過程，得到傘衣張滿時間，對得到的傘衣張滿經驗公式進行仿真驗證。

3.1 數值仿真理論基礎

本文采用LS-DYNA 軟件SALE 算法進行流固耦合仿真。該算法由流場控制方程、網格控制方程、結構控制方程組成。流場控制方程由質量方程、動量方程和能量方程組成，分別為[5-9]

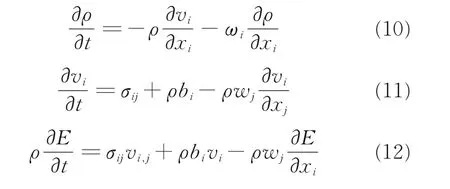
式中：vi為物質速度，wi為相對速度，wi=vi-ui，ui為 網 格 速 度；σij為 應 力 張 量，σij=-ρδij+μ(vi,j+vj,i)；bi表示單位體積力；δij為Kronecker δ-函數。

網格控制方程為

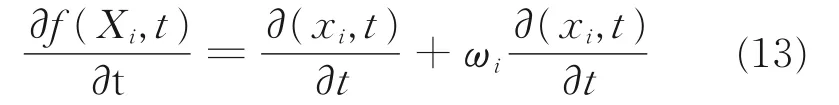
式中：Xi為拉格朗日網格坐標；xi為歐拉坐標；wi為相對速度。材料運動速度由膜的結構動力學特性決定。結構控制方程為

式中：M、C、K 分別表示單元質量、阻尼模量和彈性模量，F 為膜單元所受合力。

3.2 仿真模型建立

阻力傘放傘仿真模型由飛機、阻力傘系統、地面、流場域4 部分組成，對飛機放傘區域的流場網格進行加密，如圖6 所示[10]。

3.3 求解關鍵字設置

在提交LS-DYNA 求解器計算前，需進行關鍵字設置，包括各組成部件的單元算法、材料模型及不同部件間的耦合、接觸、連接、動網格、邊界、加載、沙漏、輸出等求解關鍵設置，以下對其中幾類關鍵設置進行說明。

(1) 流固耦合：選擇考慮透氣性的適合織物類仿真的11 號流固耦合算法。根據試驗測得的該傘衣壓差與透氣量數據，參考Ergun 公式得到傘衣透氣性的黏性和慣性兩個參數。

(2) 流場域填充：SALE 方法進行流場建模的方式和ALE 方法直接進行網格劃分不同，SALE流場域只需設置3 個維度方向的位置和網格數量，再將所定義的物質材料（空氣）對該部件進行填充。

(3) 流場域運動：在定義流場域部件，會設置其所在的坐標系，若該坐標系運動，則流場域隨之運動,若該坐標系靜止，則流場域靜止,以此途徑實現空氣域隨飛機放傘系統同步運動。

(4) 接觸：放傘過程中傘衣自身、傘衣和傘艙、傘繩和傘艙、傘衣和地面等會產生接觸，本文用到的接觸有自接觸、面面接觸和點面接觸。

(5) 動網格：通過LS-DYNA 提供的SALE 相關關鍵字進行設置，使得流場域網格與飛機同步運動，避免大規模流場域網格。

(6) 加載：設置飛機和傘系統的初始運動速度，本次計算設置其速度為300 km/h。

(7) 輸出：傘衣受力傳遞到傘繩，并通過連接帶叉帶、連接帶主部、連接繩索傳遞到飛機，設置輸出連接繩索首單元的受力曲線，并每隔0.015 s 輸出d3plot 文件。

設置完求解關鍵字，形成K 文件，將其提交LS-DYNA 求解器進行計算。

3.4 計算結果及分析

在后處理中打開d3plot 文件，可動畫播放阻力傘充氣張滿的工作過程。以阻力傘傘頂被引導傘拉出時刻為系統零點，當t=0.68 s 時，傘衣開始充氣，當t=1.30 s 時傘衣充氣張滿，如圖7、8所 示[11-13]。

圖7 傘衣開始充氣Fig.7 Canopy starting to inflate

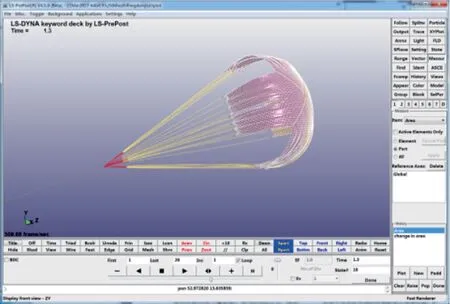
圖8 傘衣充氣張滿Fig.8 A fully inflated canopy

由此可知，傘衣張滿時間為0.62 s。該型阻力傘傘衣面積為28 m2，按照式（9）計算其張滿時間為0.65 s，仿真與理論計算較為接近，相對誤差為4.6%。

4 結 論

目前十字形傘充滿時間系數缺乏取值依據、充滿時間不易估算，利用亞聲速條件下充滿時間實測值可解算出十字形傘充滿時間系數，其圓整結果稍大于已有的密實織物傘經驗值。通過一定程度的仿真驗證表明：利用十字形傘充滿時間系數圓整結果得出的充滿時間基本準確、可信。

本文只討論了一定開傘速度下十字形傘充滿時間的估算問題，對于不同開傘速度、不同傘衣面積十字形傘充滿時間的預估，可以在本文結果的基礎上利用充滿時間與拉直速度vf的反比函數關系間接計算。