扇出型晶圓級封裝中圓片翹曲研究

張振越，夏鵬程，王成遷，蔣玉齊

（1.中國電子科技集團公司第58 研究所，江蘇無錫 214035；2.無錫中微高科電子有限公司，江蘇無錫 214035）

1 引言

隨著國內外封裝技術的發(fā)展，電子封裝技術將不斷從質量、成本和小型化等方面對產(chǎn)品制定新的更高的要求。扇出型晶圓級封裝技術是通過重構圓片的方式將芯片I/O 端口引出，在重構的封裝體上形成焊球或凸點終端陣列，其具有更高I/O 數(shù)、更小封裝尺寸、更好的散熱與電氣性能等優(yōu)勢。基于扇出型晶圓級封裝技術的3D 封裝，結合TSV 技術實現(xiàn)IC 集成封裝已成為先進封裝發(fā)展的趨勢之一[1]。

圓片翹曲是扇出型晶圓級封裝技術面臨的關鍵工藝挑戰(zhàn)之一。由于重構圓片中芯片包封材料與芯片材料的熱膨脹系數(shù)失配，導致重構圓片在溫度變化時會出現(xiàn)翹曲現(xiàn)象。翹曲的產(chǎn)生若不進行合理的控制將會嚴重影響后續(xù)工藝的進行。

國內外學者在研究晶圓翹曲的過程中，主要通過有限元仿真軟件進行計算，并根據(jù)試驗結果對仿真模型與仿真方法進行修正。Jia-Shen Lan 等人利用有限元仿真與試驗結合的方法，通過采用生死單元技術使得仿真與實測誤差在5%以內[2]。CHE 等人利用有限元仿真分析方法從材料選擇、結構設計與工藝優(yōu)化三方面研究翹曲問題，通過加入重力效應得到更精確的仿真結果[3]。CHIU 等人在研究圓片翹曲過程中考慮了材料的粘彈性行為與化學收縮[4]。翹曲方面的理論計算研究主要發(fā)展在單顆扇出封裝電路或塑封電路中。多數(shù)學者采用多層板的板殼翹曲理論進行推導，從而計算單顆封裝電路的翹曲值[5-9]。

翹曲方面的理論計算國內外學者多采用經(jīng)典板橋區(qū)理論或應變能法進行推導，本文采用彈性材料力學原理進行理論推導，提出了扇出型晶圓級封裝圓片翹曲計算的理論公式，同時針對3 種常見的工程實際問題給出計算模型的變換方式。

2 扇出型晶圓級封裝中圓片翹曲理論模型

將扇出型晶圓級封裝圓片采用雙層圓形板模型進行分析，將芯片上方的圓片作為上層板，上層板由EMC 材料組成，下層板由芯片與EMC 共同組成，利用復合材料等效方法將下層板中的芯片與EMC 等效為一種新的材料，如圖1 所示。E1、E2分別為上層板與下層板的彈性模量；α1、α2分別為上層板與下層板的熱膨脹系數(shù)；γ1、γ2分別為上層板與下層板的泊松比；h1、h2分別為上層板與下層板的厚度（即芯片的厚度）。

作用在圓形板上的載荷，對于通過中心并垂直于圓板的軸是對稱分布的，則所有與板中心等距離點的撓度是相同的，因此只需要研究一個通過對稱軸的徑向截面撓度即為圓片的翹曲值。假設圓片的橫截面在初始狀態(tài)下是平面且垂直于軸線，彎曲過程中依然保持平面并與彎曲軸垂直[10]。

圖1 晶圓級封裝圓片雙層圓形板模型

由于α1＞α2，在降溫過程中，上方圓片收縮量大于下方圓片收縮量，由于實際的圓片上下是牢固結合在一起的，故圓片必然會形成球面狀彎曲[11]。作用在上層板（EMC）上的力可以表示為橫向剪切力P1和彎矩M1，對于下層板上的力可以表示為橫向剪切力P2和彎矩M2。由于無其他外力作用，所有的力應保持平衡，則有：

由于上下層板固連在一起，上下層板在交界面處應具有相同的曲率半徑，令圓片彎曲后的曲率半徑為ρ，為上層板的抗彎剛度，為下層板的抗彎剛度[12]，則有：

帶入式（2）：

另，降溫后晶圓發(fā)生翹曲，存在約束條件：上層板與下層板在接觸面處徑向方向的變化應該相等。則有：

將式（1）與式（5）帶入式（6），并化簡得：

曲率半徑計算得到以后，即可計算圓片的翹曲值。如圖2 所示，圓片塑封冷卻后呈現(xiàn)凹型，其截面形狀即弧ACB，弧ACB 是半徑為ρ 的圓弧，即可得到：

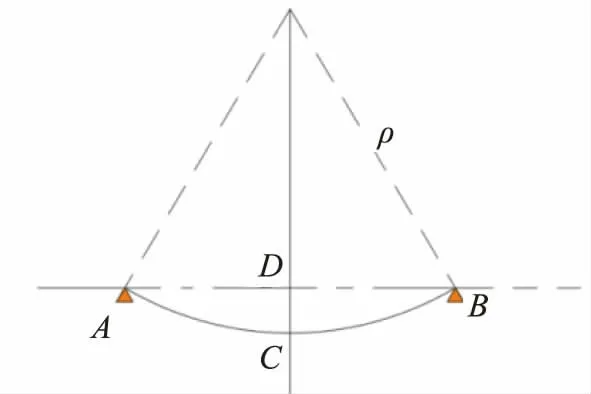
圖2 雙層圓形板的翹曲

令晶圓級封裝圓片的直徑為l，DC 為所求圓片的翹曲值δ。由于晶圓級封裝圓片翹曲值遠小于其直徑，可以認為BD≈1/2。代入式（9）得：

由于翹曲值δ 遠小于圓片直徑與曲率半徑ρ，δ2項可以忽略。同時代入曲率半徑計算公式（8）得到晶圓級封裝圓片翹曲理論計算公式：

下層板是芯片與EMC 的等效層，其材料參數(shù)為徑向線膨脹系數(shù)與彈性模量。視芯片為纖維材料，EMC 為基體，則圓片直徑X 方向材料不連續(xù)，法向Y方向材料連續(xù)，故其等效材料參數(shù)計算公式為[13]：

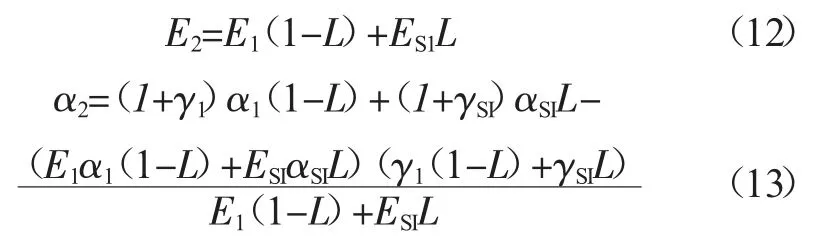
式中L 為芯片在圓片徑向方向占比，如圖3 所示。

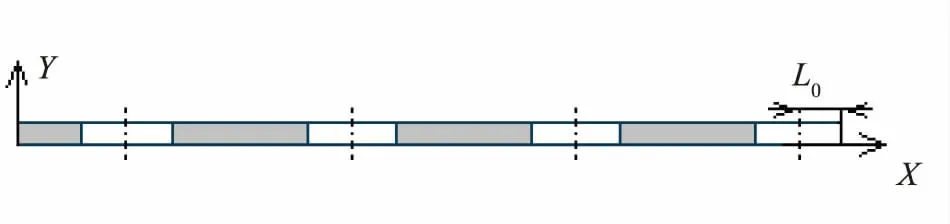
圖3 下層板芯片徑向占比示意圖

L 的計算方式有兩種：

1）對于芯片長寬尺寸與PKG 長寬尺寸采用等比擴大方式的布局方案，令扇出比為μ，扇出比為單顆封裝面積與單顆芯片面積之比。

扇出型晶圓級封裝工藝是以圓片形式的，而芯片尺寸都是正方形或長方形，為了保障各工序的進行與芯片良率，在圓片最外側會有預留，則芯片在圓片徑向方向占比L 得到以下公式：

2）存在另一部分封裝，由于設計的需要，芯片長寬尺寸與PKG 長寬尺寸并不是等比例的，這時候需要得到芯片數(shù)量與芯片尺寸才能計算L。

式中，N 為芯片在直徑方向的布局數(shù)量；L2為芯片尺寸。

3 有限元仿真與測試驗證

為了驗證上述公式，案例為某芯片進行扇出型晶圓級封裝，降溫過程為從150 ℃到25 ℃，其結構參數(shù)如表1 所示，材料參數(shù)如表2 所示。

表1 某芯片扇出型晶圓級封裝結構參數(shù)

表2 某芯片扇出型晶圓級封裝材料參數(shù)

將上述結構與材料參數(shù)分別代入式（16）、（12）、（13）、（11），根據(jù)晶圓級封裝圓片翹曲理論計算公式，計算得到圓片翹曲值為2.1022 mm。

采用有限元仿真ANSYS Workbench 軟件對某芯片晶圓級扇出圓片翹曲進行模擬計算，由于整個模型具有對稱性，采用1/4 模型進行結構建模，如圖4 所示。

圖4 某芯片扇出型晶圓級封裝結構模型

采用穩(wěn)態(tài)結構模塊，參考溫度為150 ℃，對模型整體施加25 ℃溫度載荷，設置固定點約束為芯片位于圓心處的一點，1/4 模型在X=0 面與Y=0 面設置對稱邊界條件與位移約束。根據(jù)有限元仿真計算，圓片翹曲結果為2.1418 mm，翹曲變形如圖5 所示。

圖5 某芯片扇出封裝仿真翹曲云圖

采用Shadow moire 設備測量某芯片扇出型晶圓級封裝的圓片翹曲情況，得到測試結果如圖6 所示。

圖6 Shadow moire 測試結果

理論計算、仿真、測試的結果對比如表3 所示。由于扇出型晶圓級封裝工藝中劃片、裝片、塑封、后固化等存在工藝的誤差影響，同時實際生產(chǎn)中很難達到理想的邊界條件，故無論是理論計算還是有限元仿真與實測的誤差存在是必然的。

表3 理論計算-仿真-測試結果對比

從表3 可以看出，仿真得到翹曲值與理論計算得到的翹曲值非常接近。從誤差精度看，有限元仿真與理論計算誤差都在10%以內，這是工程上能夠接受的誤差范圍。這也進一步驗證了雙層圓形板彎曲理論的假設與數(shù)學模型能夠應用于解釋扇出型晶圓級封裝中圓片的翹曲問題。

4 扇出型晶圓級封裝圓片翹曲公式的工程應用

根據(jù)式（11）～（16）可以很明顯地發(fā)現(xiàn)影響扇出型晶圓級封裝圓片翹曲的因素為圓片尺寸（l）、溫度變化范圍（t-t0）、芯片與EMC 的材料參數(shù)（E1、ESI、α1、αSI、γ1、γSI）、芯片徑向占比（L）、芯片厚度（h2）、EMC 厚度（h1）。關于材料參數(shù)對圓片翹曲的影響，多名學者已經(jīng)通過有限元仿真與參數(shù)化分析技術進行了較為詳細的研究。圓片尺寸（l）、溫度變化范圍（t-t0）由設備能力與工藝決定。

實際工程應用時，由于方案的設計或產(chǎn)品外形尺寸要求，往往出現(xiàn)以下3 種情況。

1）芯片厚度（h2）已定，需要優(yōu)選滿足工藝能力的最佳芯片扇出方案。

對式（11）進行變化：

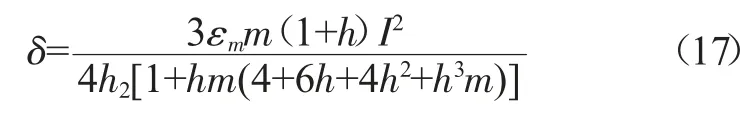
圖7 芯片徑向占比對圓片翹曲的影響關系

圖7 以芯片厚度為0.3 mm 為例，得到h 與L 對扇出型晶圓級封裝圓片翹曲的影響關系，根據(jù)設計要求與工藝能力，在圖7 中能夠對L 與h 進行選型。可見，在厚度方向，芯片的厚度占比越大，翹曲度也越低。同時，在相同硅片厚度比的情況下，芯片的徑向占比越大（芯片尺寸不變的情況下，意味著扇出比越小），圓片的翹曲度也越大。

2）封裝厚度（h1+h2）已定，需要優(yōu)選滿足工藝能力的最佳芯片扇出方案。

對式（11）進行變化：

圖8 芯片徑向占比對圓片翹曲的影響關系

圖8 以封裝厚度為0.7 mm 為例，得到h 與L 對扇出型晶圓級封裝圓片翹曲的影響關系，根據(jù)設計要求與工藝能力，在圖8 中能夠對L 與h 進行選型。

3）芯片扇出比（μ）已定，需要優(yōu)選滿足工藝能力的最佳芯片扇出方案。

利用式（15）計算得到芯片徑向占比（L），代入式（17）得到圓片翹曲值。

圖9 芯片厚度對圓片翹曲的影響關系

圖9 以芯片扇出比1.2 為例，得到h2與L 對扇出型晶圓級封裝圓片翹曲的影響關系，根據(jù)設計要求與工藝能力，在圖9 中能夠對L 與h 進行選型。

利用扇出型晶圓級封裝圓片翹曲計算公式不僅能夠針對不同產(chǎn)品快速預測晶圓的翹曲情況，對于扇出型晶圓級封裝的設計初期常見的3 個實際工程問題，根據(jù)封裝廠工藝能力與設計能力要求，選擇常用的扇出比、芯片厚度與封裝厚度，利用扇出型晶圓級封裝圓片翹曲的計算公式，能夠更好地完善封裝廠扇出型晶圓級封裝設計規(guī)則。

5 結論

本文基于雙層圓形板彎曲理論與復合材料等效方法，提出扇出型晶圓級封裝圓片翹曲理論解析表達式。通過一個實際晶圓級封裝案例進行理論求解、有限元仿真與測試。結果顯示有限元仿真結果與理論計算結果極為接近，同時與測試結果誤差在10%以內。

利用該翹曲數(shù)學模型，針對常見的3 類工程實際問題，給出了翹曲數(shù)學模型的變換方法與應用。本文提出的扇出型晶圓級封裝翹曲模型不僅能夠快速預測翹曲，而且對于晶圓級封裝產(chǎn)品的設計具有一定的指導意義，通過該翹曲模型能夠進一步完善扇出型晶圓級封裝設計規(guī)則，更好地預測與控制圓片的翹曲。