陶瓷封裝的等效熱方法及其仿真驗證

（中國電子科技集團公司第五十八研究所，江蘇無錫 214035）

1 引言

未來電子器件的發展趨勢是高集成度、高速度以及小尺寸化，這使得芯片在制造時的晶體管密度也逐漸增加，同時這也導致了芯片產生的熱量越來越大，如果不能將多余熱量散發出去，芯片的溫度就會急劇升高，從而嚴重影響芯片的性能和可靠性[1]。為了保證高集成度下的芯片能夠穩定工作，芯片的散熱設計顯得尤為重要[2]。

通過模擬仿真的方法，對不同方案的散熱設計進行對比分析，可以極大地提高散熱設計的效率。傅廣操等人[3]利用等效熱模型理論對三維堆疊中的TSV 插入層、焊接凸點層等進行了簡化，并對整體封裝進行了三維結構熱仿真，利用精確模型的仿真結果作為參照，證明了TSV 等效熱模型的可行性，為快速獲取整體結構的溫度場分析結果提供了一種可靠方法。

本文使用Icepak 熱分析軟件[4]對陶瓷封裝器件進行了仿真分析。根據JEDEC 標準中JESD51-5，對陶瓷封裝器件與測試板的連接進行了規范，即關于設置熱沉的陶瓷封裝器件可以通過在測試板上設置規定數量的銅柱進行散熱。文章對與陶瓷連接的測試板連接及散熱區域（Through Board Via，TBV）進行了熱模型等效，根據單位厚度內熱流量恒定原理，得出了關于測試板連接散熱區域的等效熱阻的計算公式。

通過T3Ster-熱阻測試儀對陶瓷器件熱阻進行測試，并將計算得到的熱阻值與仿真得到的熱阻值進行對比驗證，結果表明，通過等效熱阻模型得到的仿真值與原模型仿真得到的仿真熱阻值及實測的熱阻值具有較好的一致性，表明了等效熱模型理論的實用性。

2 封裝器件模型及材料參數

對陶瓷封裝器件與測試板的連接結構進行三維建模。其結構分別由蓋板、陶瓷基板、芯片、貼片膠、散熱片、銅片、銅柱、引腳及PCB 板組成。因為考慮到仿真計算效率的問題，對模型中的倒角、圓角及鍵合絲等對熱傳導影響較小的結構進行了適當簡化，得到模型如圖1 所示，材料參數如表1 所示。

圖1 陶瓷封裝體與測試板連接結構圖

表1 材料參數

3 封裝器件熱模型等效

3.1 等效模型單元提取

對陶瓷與測試板連接區域（TBV）的熱模型進行等效，即將銅片與PCB 等效成一塊各向異性的單元塊，同時將銅柱與PCB 等效成一塊各向異性的單元塊。此時，單元塊在x-y 向和z 向的熱導率呈各向異性。簡化需要滿足一定的條件：（1）簡化前后的尺寸保持不變；（2）等效前后的模型傳熱效果保持不變，即等效單元塊的熱導率與實際模型等效熱導率相同。如圖2(a)所示為等效前的模型側面視圖，圖2(b)為等效后的模型側面視圖。

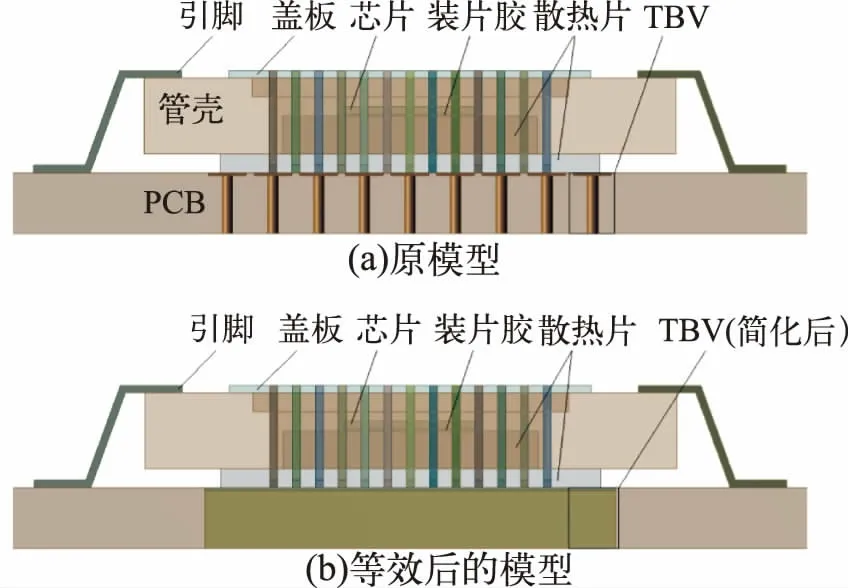
圖2 模型側面視圖

對連接的TBV 區域展開為平面圖，如圖3 所示，將需要陣列等效的區域分為兩塊，一塊為由PCB 環繞的銅片陣列，另一塊為由PCB 環繞的銅柱陣列，分別提取其單元如圖3(a)、(b)所示。

圖3 單元塊提取圖

3.2 等效模型熱導率計算

熱阻是指熱量傳遞通道上兩個參點之間的溫度差與熱源功率之間的比值[5]，如式（1）所示：

其中，R 為兩點間的熱阻（單位℃/W 或K/W），△t 為兩點間的溫度差（單位℃），P 為兩點間的熱源功率（單位W）。

導熱基本公式為：

其中，L 為熱傳導距離（單位m），S 為熱傳導截面積（單位m2），K 為熱導率（單位W/m℃）。根據式（1）和式（2），得到熱傳導模型的熱阻計算公式：

由式（3）可知，熱傳導距離越短、截面積越大以及材料的熱導率越高，兩點之間的熱阻值越低。因此，在封裝設計中采用合理的結構和選用合適的材料，對減小封裝器件的熱阻起到了至關重要的作用。

通過對式（3）進行變換，得到式（4）：

根據單元塊的對稱性，取1/2 模型單元作為分析對象。如圖4(a)所示是PCB 環繞銅柱陣列單元塊，圖4(b)為焊柱簡化后的單元塊，其中a 為單元塊的長度，r為焊柱的半徑。

圖4 PCB 環繞銅柱陣列單元塊

先計算PCB 環繞銅柱陣列單元塊的熱阻。在z 方向，其單位長度等效熱阻有如下關系式[3]：

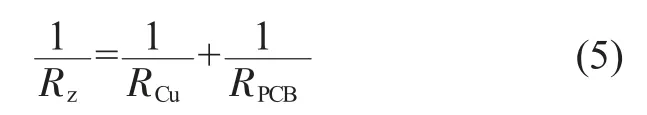
其中RCu、RPCB為單位長度的熱阻。

其中KCu、KPCB分別為銅的熱導率和PCB 的熱導率。

根據式(4)可知，單位長度上的z 方向等效熱導率為：

令α=2r/a，結合式(6)、(7)、(8)得到式（9）：

對于x、y 方向，采用相同的方法可以得到其單位長度等效熱阻為：

結合式(4)、(10)可得，單位長度上x、y 方向上的等效熱導率為：

代入數據a=1.2 mm，r=0.15 mm，得到PCB 環繞銅柱陣列單元塊的等效熱導率Kxy=35.73，Kz=217.14。

圖5 PCB 環繞銅片陣列單元塊

PCB 環繞銅片陣列單元塊如圖5 所示，使用上述相同的計算式，帶入數據a=1.2 mm，r=0.5 mm，可得其等效熱導率Kxy=24.82，Kz=19.89。

4 封裝器件結環境熱阻仿真

通過Icepak 熱分析軟件分別對原模型及等效后的模型進行自然對流下的結環境熱仿真，設置芯片發熱功耗為2.4 W，環境溫度為25 ℃，仿真得到等效模型和原模型的芯片結溫分別為53.81 ℃、51.37 ℃，其溫度分布的云圖分別如圖6、圖7 所示。通過式(1)計算得到原模型和等效模型結到環境的熱阻分別為11℃/W、12 ℃/W，整理得到結環境熱阻的條件及結果如表2 所示。

表2 結-環境熱阻仿真結果

圖6 結環境熱仿真溫度分布云圖(原模型)

圖7 結環境熱仿真溫度分布云圖(等效模型)

5 熱仿真及結果對比驗證

根據JEDEC 標準中JESD51-1、JESD51-2 熱阻測試方法，將焊接在PCB 板上的封裝器件放置在靜止空氣測試箱中進行測試，同時使用熱電偶探測得到靜止空氣測試箱中的環境溫度，根據熱阻計算公式θja=(tjta)/P 計算出封裝器件結-環境熱阻θja。

測試中采用1 A 加熱電流，1 mA 測試電流。取3個樣品通過熱阻測試設備進行測試，得到封裝器件測試的平均結溫如表3 所示，熱阻測試結構曲線如圖8所示。通過計算，得到實際工況下封裝器件的結-環境熱阻（θja）測試結果為10.86 ℃/W。

表3 結-環境熱阻測試結果

圖8 封裝器件熱阻測試溫度曲線圖

通過實測及計算得到陶封器件的結環境熱阻值為10.86 ℃/W，仿真計算得到陶封器件在等效熱模型下的結環境熱阻值為11.32 ℃/W，原模型的結環境熱阻為11 ℃/W。等效熱模型下的結環境熱阻值是實際熱阻值的4.2%，原模型的熱阻值是實際熱阻值的1.3%，其熱阻值與實測值對比的偏差均在5%以內，因此通過等效熱模型的方法可以獲得精度較高的陶瓷封裝器件的結環境熱阻值[6]。

6 結論

本文利用等效熱模型理論，對用于陶瓷封裝器件測試的PCB 及其銅柱的熱阻進行了等效計算，通過對等效熱模型與原模型進行結環境的熱仿真，得到了等效熱模型的熱阻值與原模型熱阻值，與實際熱測試的阻值對比有良好的一致性，其偏差均在5%以內，表明了所采用的等效熱模型仿真計算方法的可行性，為陶瓷封裝器件在PCB 等復雜模型中的組合熱仿真計算提供了一種簡單可行的方法。