基于公共天氣預報的三江平原ET0預報模型比較及敏感性分析

錢 坤，陳夢婷，沈瑩瑩，胡旭鏵，金 麗，劉少輝，崔遠來，羅玉峰

（1.武漢大學水資源與水電工程科學國家重點實驗室，武漢430072；2.中國灌溉排水發(fā)展中心，北京100054；3.黑龍江省富錦市錦西灌區(qū)建設管理站，黑龍江富錦156100）

近年來，三江平原存在農墾區(qū)水稻種植面積不斷擴張的現象[1]，為滿足作物生長的需要，作物用水量日益增長。為保障三江平原地區(qū)水安全和糧食安全，維持供需水的平衡，需要大力發(fā)展節(jié)水灌溉農業(yè)。節(jié)水灌溉的核心是實行計劃用水，而計劃用水的關鍵在于灌水預報[2]。灌水預報依賴于作物需水量預報，而利用參考作物騰發(fā)量（Reference crop evapotranspiration，ET0）與作物系數的乘積可以得到作物需水量。因此，精確、及時的ET0預報對于發(fā)展三江平原節(jié)水灌溉具有重要意義。

根據分析方法和輸入數據的不同可以將ET0預報分為2類，即直接法和間接法[3]。直接法以歷史ET0數據為輸入，采用時間序列方法進行預報，國內外對此均有研究。Tracy[4]等提出了時間序列模型用以預報ET0，在加利福尼亞州取得了較好的預報精度；馮培存等[5]針對溫室甜瓜耗水量研究，建立了基于思維進化算法優(yōu)化BP 神經網絡的參考作物蒸散量預測模型，大大降低了模型預報誤差。隨著公共天氣預報精度的不斷提升，以氣象數據和溫度模型作為基礎的間接法ET0預報受到較多關注和研究。蔡甲冰等[6]提出了一種將日天氣預報信息轉化為計算ET0所需變量的分析方法，并利用FAO56-PM 公式預報了ET0；羅玉峰等[7]根據南京站的氣象數據及天氣預報數據信息，提出了精確度較高的利用HS 公式預報逐日ET0的方法；馮軍等[8]選取荊州站多年氣象資料，對HS、PT、MC、IA 4 種公式計算的ET0結果進行分析比較，得出了HS 與PT 公式較為適用的結論。

由于間接法大多基于天氣預報數據和模型進行ET0預報，氣象因子的精確度對最終模型的輸出結果具有一定影響，因此需要研究氣象因子預報誤差對預報模型輸出結果的影響，即需要進行預報模型對氣象因子的敏感性分析。王碩等[9]基于PLPM模型采用改進的摩爾斯分類篩選法，將黃土高原98個站點ET值結果對各氣象因子進行了敏感性分析研究，確定了各參數的敏感程度并提高了模型反演精度。

目前，天氣預報預測ET0的研究大多局限于單一模型的校正應用，缺乏其他多種模型的比較和擇優(yōu)[10]。關于三江平原ET0預報較少，且較少有學者在此基礎上進行進一步的敏感性分析。本文基于三江平原6 個氣象站點的數據，計算得到Penman-Monteith標準值，比較Hargreaves-Samani （HS）、Thornthwaite（TH）以及Blaney-Criddle（BC）3 種模型的ET0預報精度，從而得到適用于三江平原的最優(yōu)ET0預報模型，并對該最優(yōu)模型進行溫度敏感性分析，以期為實際生產應用中的灌溉預報提供準確的ET0預報依據。

1 數據與方法

1.1 區(qū)域概況

三江平原位于黑龍江省的東北部（45°01′N～48°27′N，130°13′E～135°05′E），總面積10.89萬km2，耕地面積占總面積的比例為44.85%[11]。屬溫帶濕潤、半濕潤大陸性季風氣候，夏季炎熱濕潤，冬季嚴寒干燥。地勢低平，由西南向東北傾斜，平均海拔50～60 m，區(qū)域內分布有多個國家氣象站點，氣象數據較易準確獲得。本區(qū)域地表水及地下水資源豐富，受作物特性和生長環(huán)境影響，水稻高產穩(wěn)產，是我國重要糧食產區(qū)。

1.2 數據源

由中國氣象數據網(http：∕∕data.cma.cn)收集了三江平原6個站點（富錦50788，佳木斯50873，依蘭50877，寶清50888，雞西50978，虎林50983）2012年1月1日至2018年6月30日的歷史氣象實測數據，實測數據包含最高溫度、最低溫度、平均風速、日照時間、平均相對濕度。天氣預報數據來自智慧灌溉管理平臺(http：∕∕www.smartirrigation.org)，收集了6 個站點2017年1月1日至2018年6月30日預見期為1～7 d的天氣預報數據，包含了日最高氣溫、日最低氣溫。

1.3 預報模型

1.3.1 FAO56-Penman-Monteith模型（FAO56-PM模型）

1998年聯(lián)合國糧食與農業(yè)組織推薦Penman-Monteith 公式為計算ET0的標準方法，該法計算精度高，理論可靠，可用來作為基準值驗證其他經驗公式的計算精度[12]。該公式表述如下：

式中：ET0,PM為FAO56-PM 公式計算得到的ET0值，mm∕d；Rn為地表凈輻射，MJ∕（m2·d）；G為土壤熱通量，MJ∕（m2·d）；T為平均氣溫，℃；u2為2 m 高度處的風速，m∕s；es和ea分別為飽和水汽壓和實際水汽壓，kPa； Δ 為飽和水汽壓～氣溫曲線上的斜率，kPa∕℃；γ為濕度計常數，kPa∕℃。

1.3.2 Hargreaves-Samani模型（HS模型）

2003年Hargreaves and Allen[13]提出了一種僅基于氣溫數據計算參考作物蒸發(fā)蒸騰量ET0的簡化模型，簡稱為HS公式：

式中：ET0,HS為HS 公式計算得到的ET0值，mm∕d；Ra為大氣頂太陽輻射，MJ∕（m2·d）；Tmax為最高氣溫，℃；Tmin為最低氣溫，℃；C、E為公式中的2 個參數，FAO 給出的建議值分別為0.002 3和0.5，但是由于不同地域氣候類型的差異性，參數C、E表現出地區(qū)變異性，需要進行校正[14]。

1.3.3 Thornthwaite 模型（TH模型）

Thornthwaite 經驗公式基于美國中東部地區(qū)的試驗數據提出，其將ET0看作溫度的冪函數，并假設干濕空氣無平流，潛熱與顯熱比為常數[15]。它是依據月平均氣溫和最大可能日照時數建立聯(lián)系的一個計算月平均ET0的經驗公式。考慮到部分地區(qū)冬季月平均溫度在0 ℃以下，采用改進后的TH模型：

式中：ET0,TH為TH 公式計算得到的ET0值，mm∕d；I為熱量指數；Tef為有效的每日溫度，Tef=0.5(3Tmax-Tmin)，℃；k為常數，以k=0.72估計月平均ET0，結合轉換系數C計算逐日ET0；C為轉換系數，C=N∕360，N為給定天數的光周期，h。

I的計算公式為：

式中：Tn為月平均溫度（若Tn＜0，則取Tn=0），℃。

α為I的函數：

1.3.4 Blaney-Criddle模型（BC模型）

Blaney-Criddle模型由Blaney 和Criddle 于1962年提出[16]。BC模型認為，在土壤水分供應充足時，ET0可通過時段內平均氣溫和平均白晝小時占全年白晝小時數的百分比進行計算。該公式為：

式中：ET0,BC為BC 公式計算得到的ET0值，mm∕d；p為時段內日白晝長度占全年白晝長度的百分比，%；T為時段內平均溫度，℃。

1.4 參數率定

運用實測氣象數據，計算得到Penman-Monteith 標準值，對HS、TH、BC模型進行校正和檢驗，其中2012-2016年為校正期，2017-2018年為驗證期。對于HS 模型，由于其自身包含反映地區(qū)特異性的參數C和E，采用非線性最小二乘法擬合率定出參數C、E。TH和BC模型則采用線性擬合進行校正：

式中：ET0,PM為基于PM 公式計算得到的ET0值，mm∕d；ET0,j為其他模型計算得到的ET0值，mm∕d；a、b為待率定的參數。

1.5 統(tǒng)計分析指標

采用平均絕對誤差（mean absolute error，MAE）、均方根誤差（root mean square error，RMSE）及相關系數（correlation coefficient，r）3項統(tǒng)計學指標評估天氣預報精度及ET0預報精度[17]。定義預報最高和最低氣溫絕對誤差在±2 ℃以內的天數占總數樣本個數的百分比為氣溫預報的準確率[18]（accuracy，Acc）。各指標計算公式為：

式中：xi為氣溫預報值或各模型ET0預報值；yi為氣溫實測值或ET0,PM；i為預報樣本序數，i=1，2，…，n；、分別為預報值、計算值或實際值序列的均值；nacc為氣溫預報準確的天數；n為預報值的樣本數。

1.6 敏感性分析

為探究溫度預報誤差的影響，采用單因子法對ET0預報誤差進行敏感性分析，計算最優(yōu)模型預報結果對最高溫和最低溫的敏感性。單因子法簡單方便，容易比較分析出各變量對輸出結果的影響程度差異，但其只能反映某個自變量因素對輸出結果的影響，無法反映各變量同時變化對于最終結果的影響。因此本文還使用了多因子法敏感性分析，即考慮最高溫、最低溫2 個輸入變量同時變化對ET0輸出結果的影響。將四季內最高、最低溫和各模型ET0值的均值作為基準值，當氣溫預報誤差范圍為±20%，以5%為步長變動，單因子法每次只變動一個變量另一個不變，多因子法2變量均變化，計算對應的ET0值相對于基準值的變化。

2 結果與分析

2.1 天氣預報精度評價

表1為6個站點在2017-2018年預見期1～7 d時逐日天氣預報的各項統(tǒng)計指標平均值。由表1可知，隨著預見期天數的增加，最高和最低氣溫的預報表現總體上呈下降趨勢，準確率下降，反映離差和離散程度的MAE和RMSE逐漸增高，相關性逐漸下降。最高和最低氣溫預報準確率的變化范圍分別是46.34%～78.01%、47.31%～51.21%；MAE的變化范圍為1.31～2.65 ℃及2.46～2.67 ℃；RMSE的變化范圍分別是1.86～3.42 ℃及3.23～3.48 ℃；最高和最低氣溫預報值與實測值的相關系數r都相對較高，分別為0.93～0.98 及0.95～0.97，表明預報值與實測值之間有較強的線性相關關系。綜上所述，三江平原6個站點高溫預報的準確率要高于低溫，但6 個站點各項預報的MAE、RMSE及r大部分均表現優(yōu)良，預報準確率較高，這說明氣溫預報精度良好，溫度預報可以用于ET0預報之中。

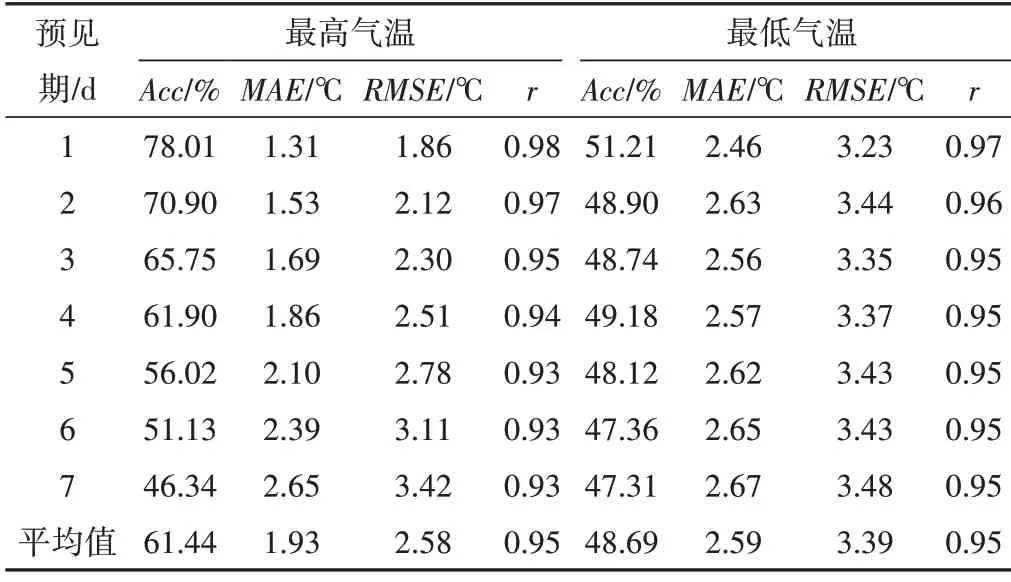
表1 6個站點氣溫預報精度統(tǒng)計指標平均值Tab.1 Average values of statistical index of temperature forecast precision at 6 stations

2.2 ET0預報模型地區(qū)校正與驗證

3 種模型參數的率定結果如表2所示。經過率定后，6 個站點的C值范圍為0.000 6～0.000 8，落在胡慶芳等[19]給出的分布區(qū)間[0.000 5，0.002 0]內，且與其給出的建議值0.000 8非常接近，E值范圍為0.500～0.653，與給出的區(qū)間有部分差異，這可能是因為不同年份降水量的差異以及選擇的時間步長不同導致，胡慶芳以逐月作為研究的時間步長，而本文以逐日作為時間步長。

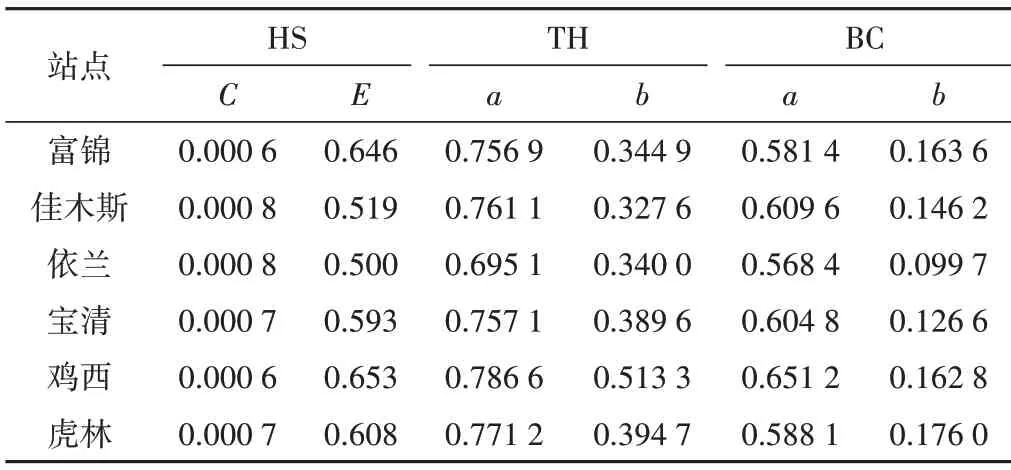
表2 3種模型參數率定結果Tab.2 Calibration results of the three temperature-based models

表3為3 種預報模型預報精度各項統(tǒng)計指標結果。表3中6 個站點的MAE、RMSE均在1 mm∕d 以內，校正值與真實值非常接近，離散程度小；相關系數r都達到了0.85以上，校正后的模型計算值與基準值相關性很高，變化趨勢基本保持一致。說明在經過參數本地化的修正后，各模型計算值與PM 模型標準值已經很靠近，3 種模型的性能均得到了比較明顯的改善，ET0的計算精度都很高，誤差較小，校正效果可行。因此，校正后的模型可以應用到ET0預報中。

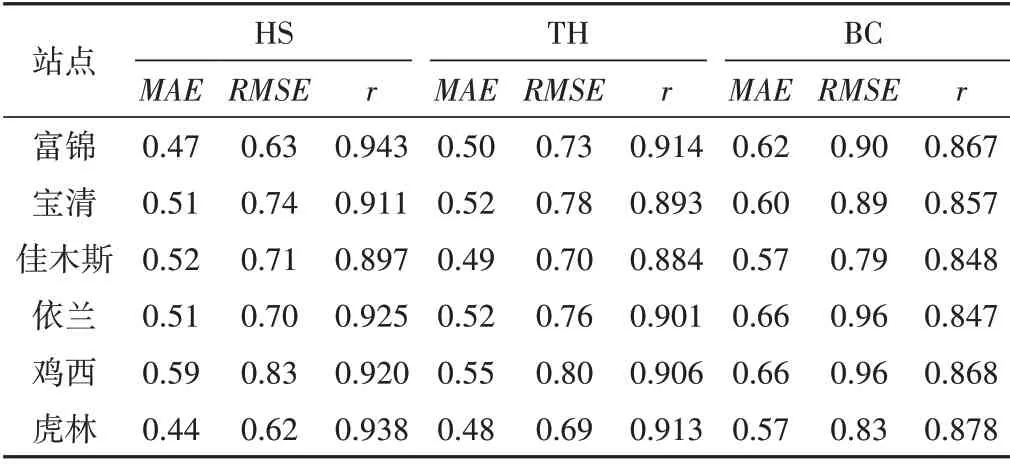
表3 驗證期各校正模型ET0值精度統(tǒng)計指標 mm∕dTab.3 Statistical indices for the calculated ET0 of each model during the validation period

2.3 基于公共天氣預報的ET0預報

2.3.1 預報結果

各修正模型在6 個站點上ET0預報的統(tǒng)計指標平均值如表4所示。隨著預見期天數的增加，ET0預報精度總體上呈下降趨勢，相關系數r下降，反映誤差和離散程度的MAE和RMSE在逐漸增高，說明誤差越來越大，與氣溫預報精度變化規(guī)律一致。從連續(xù)7 d 的預報水平來看，3 種模型ET0預報MAE的變化范圍分別為0.56～0.72、0.58～0.69、0.63～0.67 mm∕d，RMSE的變化范圍分別為0.78～1.02、0.85～1.04、0.91～0.95 mm∕d，相關系數r的變化范圍分別是0.827～0.901、0.799～0.867、0.829～0.853。3 項指標隨著預見期的增加，波動幅度都在比較小的范圍內。模型預報誤差均很小，與基準值的相關性高，3 種修正后的預報模型基于公共天氣預報得到的ET0值預報精度均較高。

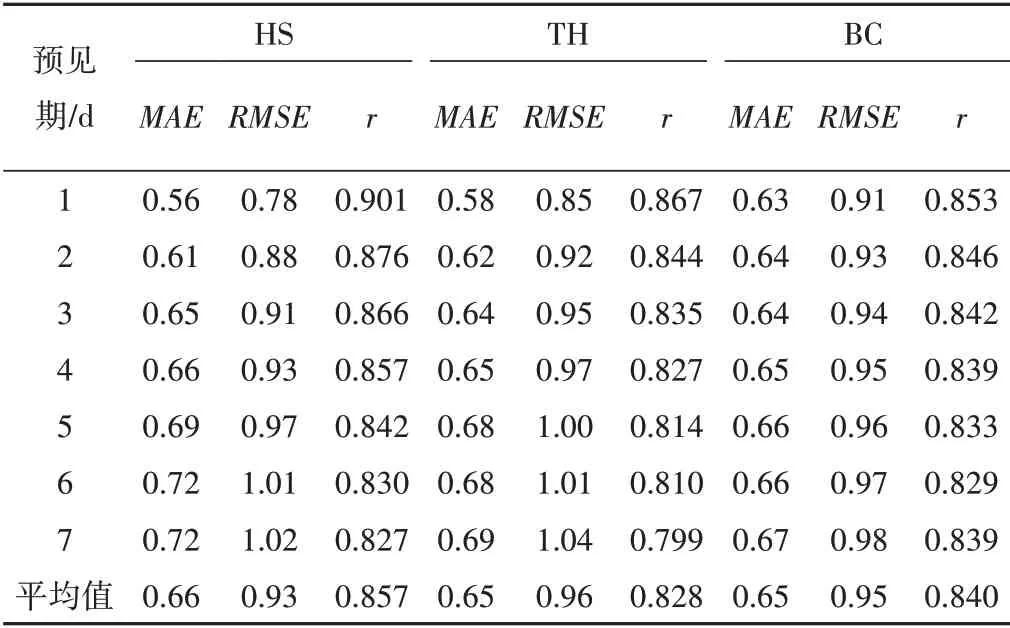
表4 各修正模型ET0預報精度統(tǒng)計指標平均值 mm∕dTab.4 Average values of statistical indices for the ET0 forecast precision of each corrected model

2.3.2 最優(yōu)模型

圖1為3 種模型的ET0預報值與ET0，PM值變化過程圖，除去少量的過高過低的預測值，修正后各模型的預測值與PM 公式計算得到的標準值大致相同，預測值與標準值總體上的變化趨勢保持同步，總體上來說，3 種模型預報值均比較準確。其中HS 和TH 模型計算值與PM 模型重合度較高，BC 的重合度最低。

結合前面表4可知，HS 模型的MAE最小，r最大，RMSE與TH、BC 模型相差很小，在預見期1～5 d時，HS預報模型至少有2 項指標優(yōu)于另外2 種模型，最近的1～2 d 時3 項均最優(yōu)，這說明在預見期較短時HS 模型精度最高，預見期增長時總的來說其預報精度也是最高的。綜合3 項指標及ET0變化過程圖來看，HS 模型表現最好，可以確定HS 模型為三江平原最優(yōu)ET0預報模型。

2.4 敏感性分析

單因子法模型輸出結果誤差如圖2所示。以富錦為例，HS 修正模型對最高溫預報敏感性最大的為夏季，當最高溫度預報圍繞季節(jié)平均最高溫度波動-20%～20%時，ET0預報誤差為-1.67 ～1.61 mm∕d，遠遠大于其他3個季節(jié)，另外3季敏感性由低到高分別為春、秋、冬，冬季時預報模型對最高溫預報敏感性最小，最大波動不超過±0.1 mm∕d。在夏季時，HS模型對于最低溫預報敏感性也最大，當最低溫度預報圍繞季節(jié)平均最低溫度波動-20%～20%時，ET0預報誤差為-0.81～0.68 mm∕d，比其他3 個季節(jié)誤差大得多，冬季敏感性最小。由此可知，HS 模型預報值在夏季時對于溫度預報最敏感，此時ET0預報結果受溫度預報誤差影響最大。此外，最低溫度預報誤差導致的ET0預報誤差普遍比最高溫預報誤差引起的ET0預報誤差要小，即預報誤差對低溫更不敏感。

多因子法敏感性分析中4 季ET0預報值受溫度預報影響結果如圖3所示。由圖3可知，與單因子法敏感性分析時得到的結論相同，在夏季時ET0預報受溫度預報誤差影響最大，ET0預報誤差范圍為-3.22～1.10 mm∕d；冬季時ET0預報受溫度預報誤差影響最小，誤差范圍為-0.37～0.22 mm∕d。就ET0預報誤差值而言，正誤差最大值出現在最高溫度預報波動20%、最低溫度預報波動-20%時，而負誤差最大值出現在最高溫度預報波動-20%、最低溫度預報誤差波動20%，且負誤差遠大于正誤差。由此可知，當最低溫度的預報誤差由低估到高估正向逐漸變大、最高溫度預報誤差由高估到低估負向逐漸變小時，ET0預報誤差開始由正到負不斷變化，而在此過程中ET0預報對于溫度預報誤差越來越敏感。

在多因子法分析下，大多時候最高溫、最低溫預報誤差組合導致的ET0預報誤差值比單因子法分析下更小，集中在0.5 mm∕d以內，即在最高、最低溫度預報均可能產生誤差的實際情況下，ET0預報誤差并不會增大。因此，HS修正模型因溫度預報誤差而產生的誤差是相對有限、可以接受的。

3 結 論

本文基于公共天氣預報，采用HS、TH、BC 模型對三江平原ET0預報開展研究并進行了相應的模型敏感性分析，得到如下結論。

（1）三江平原公共天氣預報精度較高，ET0預報模型的修正效果良好，可以用于ET0預報計算。

（2）將天氣預報數據代入修正后模型得到ET0預報值分析其精度，結果顯示，HS、TH、BC 這3 種模型1～7 d 預見期MAE均值分別為0.66、0.65、0.65 mm∕d，RMSE分別為0.93、0.96、0.95 mm∕d，r分別為0.857、0.828、0.840。HS 模型精度最高，TH 模型次之，BC 模精度最差，推薦HS 修正模型為三江平原ET0預報模型。

（3）單因子法敏感性分析結果顯示，在夏季時HS 模型對溫度預報誤差的敏感性更大，在冬季時對溫度預報誤差的敏感性更小。ET0預報誤差對于高溫預報的誤差更敏感。多因子法敏感性分析與單因子法的結果相同，在夏季時ET0預報誤差對溫度預報誤差的敏感性大于冬季。4季整體誤差較小，在可接受范圍內。