單翼迷宮式滴灌帶的關鍵參數與灌水均勻度的響應關系

2021-05-07 06:36:12陶洪飛如蘇力努爾畢金錄阿卜杜賽麥提托乎提麥麥提艾則孜艾力阿卜來提阿不杜熱依木

節水灌溉 2021年4期

張慧，陶洪飛，如蘇力·努爾，畢金錄，阿卜杜賽麥提·托乎提，麥麥提艾則孜·艾力，阿卜來提·阿不杜熱依木

（1.新疆農業大學水利與土木工程學院，烏魯木齊830052；2.新疆水利工程安全與水災害防治重點實驗室，烏魯木齊830052）

0 前言

水資源危機是我國干旱半干旱地區共同面臨的問題，節約灌溉用水是緩解我國水資源危機的一項重要措施[1]。滴灌帶由于其良好的節水性能被廣泛使用。灌水均勻度[2]是衡量滴灌系統是否符合灌溉標準的重要性指標，直接影響整個滴灌系統的灌水質量和工程造價[3]。在前人研究過程中已經對灌水均勻度進行了大量的研究。羅春艷[4]研究發現隨著進水口壓力變化滴頭流量發生變化，從而影響灌水均勻度，灌水均勻度隨壓力增大呈上升趨勢。王宏[5]研究發現灌水均勻度隨鋪設長度的增加呈下降趨勢，其原因是滴頭損失隨著鋪設長度增加呈增大趨勢，從而使灌水均勻度發生改變。常換換[6]研究發現在壓力不變的條件下，灌水均勻度隨著坡度增加呈先增大后減小趨勢。

目前，在設計滴灌工程時一般考慮制造偏差[7,8]、滴灌帶鋪設坡度[9,10]、工作壓力[11-13]、滴頭堵塞[14-16]等因素對灌水均勻度的影響。在前人研究過程中，一般只研究1 種或2 種因素對灌水均勻度的影響，但同時研究3種因素對灌水均勻度的影響且建立有效預測模型的研究鮮有報道。本試驗在前人研究的基礎上，對3種型號的單翼迷宮式滴灌帶在不同鋪設坡度、工作壓力和長度條件下分析，并運用投影尋蹤回歸（PPR）方法建立灌水均勻度與3種影響因素的數學模型，以期為滴灌系統的應用和發展提供理論依據和科學指導。

1 試驗材料與方法

1.1 試驗材料與設備

每組試驗使用新疆某公司生產的單翼迷宮式滴灌帶3 條，滴灌帶參數見表1。試驗研究在新疆農業大學農業水利工程實驗室的滴灌帶(管)抗堵塞性能測試平臺上進行（試驗裝置見圖1）。其中主控柜包括供加壓系統、水壓力控制系統、壓力傳感器等部分。

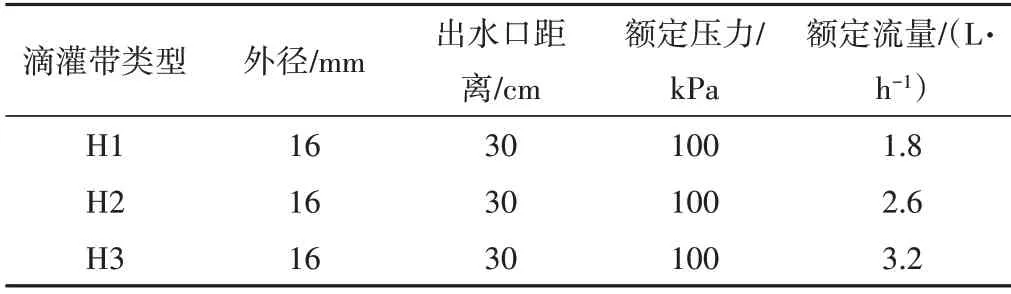
表1 滴灌帶水力性能參數Tab.1 Hydraulic performance parameters of drip irrigation belt

1.2 試驗方案設計

（1）單因素試驗。在其他條件不變的情況下做壓力40、50、60、70、80、90、100、110、120、130 kPa 的單因素試驗。

（2）均勻正交試驗。選擇鋪設坡度、工作壓力、鋪設長度3 個因素作為參選因素（分別標記為A、B、C），每因素選取3 個水平（見表2），選用均勻正交設計表UL9（34）進行試驗方案的設計。

表2 因素與水平Tab.2 Factors and levels

1.3 試驗方法與步驟

由計算機設定測試壓力值，取樣時間為10 min，同時對3根單翼迷宮式滴灌帶進行試驗，其中2根為對照試驗，每根單翼迷宮式滴灌帶等間距選擇25 個滴頭，并由量杯收集水量（1 000 mL），采用質量法計算出水流量。

1.4 數據計算與處理

（1）流量均勻性計算。單翼迷宮式滴灌帶的流量均勻性用滴水孔流量的變異系數（CV）和流量偏差率（C）來綜合判定。

（2）滴灌的均勻度。滴灌的均勻度通常以克里斯琴森均勻系數表示：

式中：Cu為滴灌的均勻系數；為各滴頭的平均流量，L∕h；qi為各滴頭流量，L∕h；N為測試的滴水孔數。

（3）數據處理。所有試驗數據采用Excel 2013 進行整理和計算，采用SPSS 23.0 軟件進行統計分析，采用PPR 軟件進行數學建模。

2 結果與分析

每個處理完成后，統計并計算每個出水孔的流量，由式（4）計算出每個處理的灌水均勻度。表3為試驗結果，表3數據均為3次取樣的平均數。對試驗數據進行直觀分析、方差分析及多重比較分析。

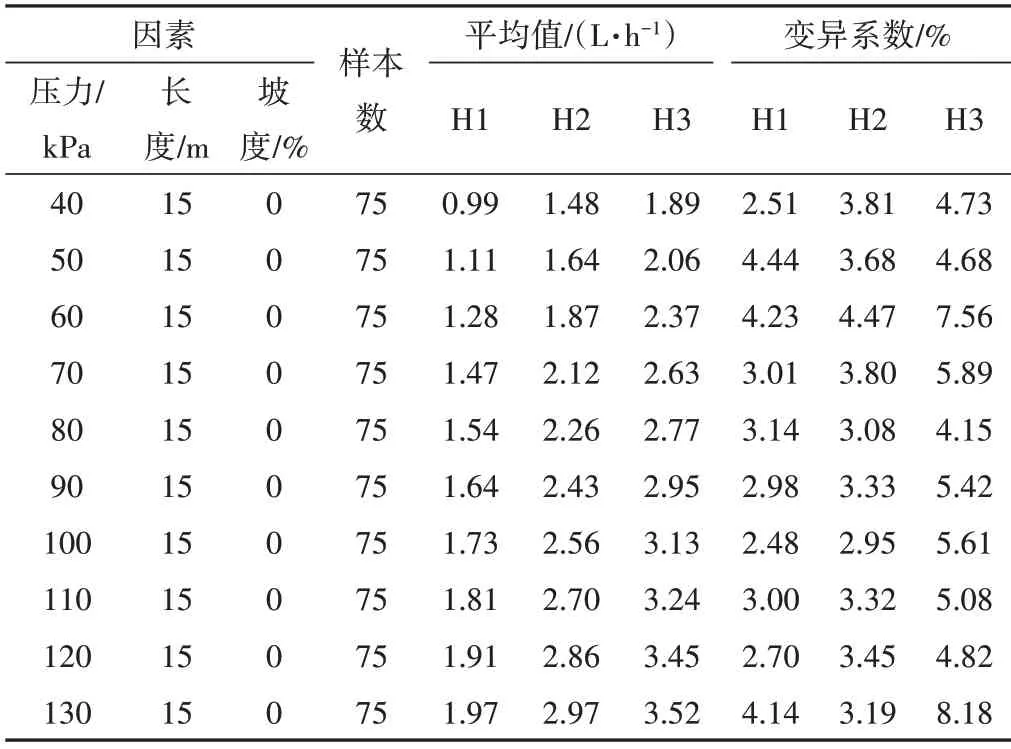
表3 流量統計與分析Tab.3 Traffic statistics and analysis

2.1 滴頭流量統計與分析

將表3中H1、H2、H3壓力40～130 kPa變化下的滴頭流量數據輸入到Excel 2013生成散點圖，并添加趨勢線，擬合程度R2分別為0.990、0.996、0.994，說明趨勢線擬合程度非常好。表4為計算所得滴灌帶流量系數與流態指數。在額定壓力100 kPa 和坡度為0%時由公式（1）和（3）計算得到偏差率和變異系數結果見表4。3 種型號單翼迷宮式滴灌帶流量偏差率C均小于7%，滴水孔流量的變異系數CV均小于7%[17]，因此判定3種型號單翼迷宮式滴灌帶均為優等品[18]。

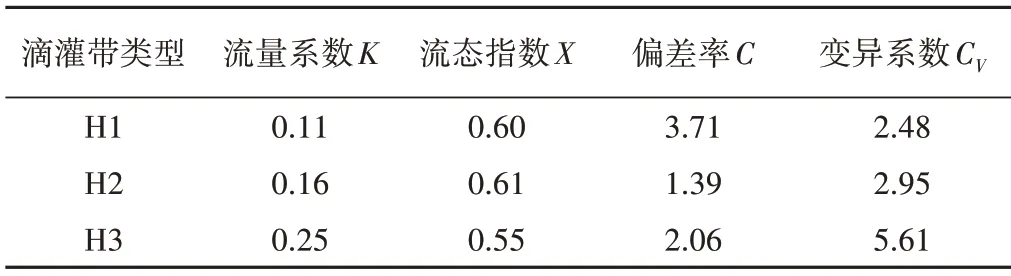
表4 滴灌帶參數Tab.4 Drip irrigation belt parameters

在壓力40～130 kPa的10組試驗中H1滴灌帶平均變異系數為3.263，H2 滴灌帶平均變異系數為3.508，H3 滴灌帶平均變異系數為5.612。這說明H1滴灌帶在各試驗條件下滴頭流量較為穩定，而H3 滴灌帶相對較差，3 種滴灌帶穩定性依次為H1＞H2＞H3。由表3可知，變異系數隨著單翼迷宮式滴灌帶滴頭流量的增大呈上升趨勢，這可能與流道參數和制造偏差有關，本試驗未考慮這方面的影響，建議后續研究者可以著重這方面的研究。

2.2 極差分析

從表5可知影響H1、H2、H3型單翼迷宮式滴灌帶灌水均勻度的主次因素次序為進水口壓力＞鋪設長度＞鋪設坡度。H1、H2、H3 型滴灌帶空白列極差均小于3 個因子的極差，故不考慮因子間相互作用。極差分析法無法判斷試驗因素（進水口壓力、鋪設長度、鋪設坡度）對試驗結果（灌水均勻度）是否具有顯著性的影響，為了解決這個問題，下文將對試驗數據進行方差分析與多重比較。試驗方案及結果見表6。

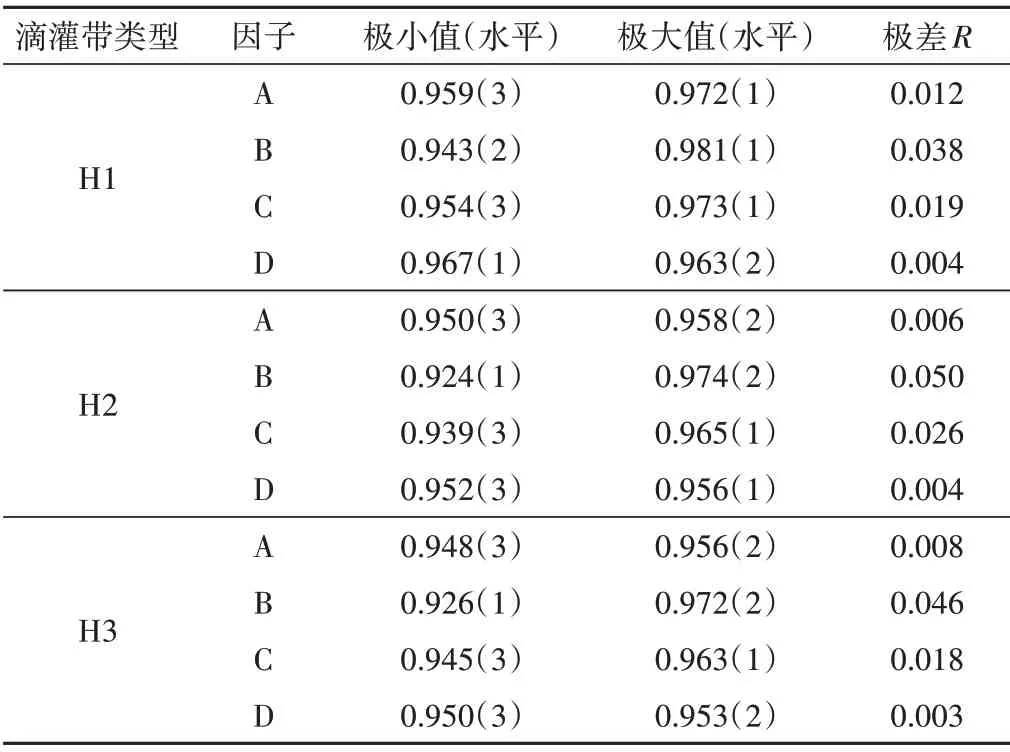
表5 直觀分析Tab.5 Intuitive analysis

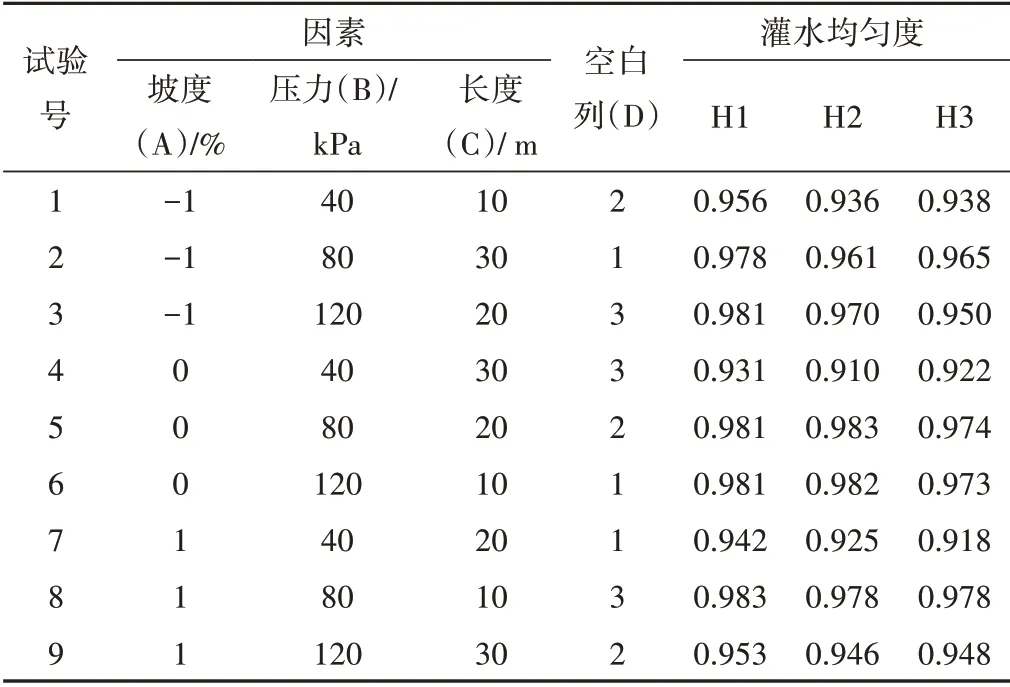
表6 UL9（34）均勻正交設計與試驗結果Tab.6 Unifom orthogonal design and experimental results of UL9（34）

2.3 方差分析和多重比較分析

（1）方差分析。方差分析結果見表7，方差齊性檢驗結果顯示數據滿足方差齊性，且殘差顯示滿足均值為0的正態分布。表7可以看出，H1、H2和H3型顯著性規律相似，均為進水口壓力對單翼迷宮式滴灌帶灌水均勻度影響最大，達到極顯著水平；鋪設長度對單翼迷宮式滴灌帶灌水均勻度的影響達到顯著水平；鋪設坡度對單翼迷宮式滴灌帶灌水均勻度的影響不顯著，影響單翼迷宮式滴灌帶灌水均勻度的因素顯著性依次為：進水口壓力＞鋪設長度＞鋪設坡度，這與極差分析一致。張國祥等[19]研究發現當地形較為平緩時坡度變化對灌水均勻度的影響極小，這與本試驗結果相同。單翼迷宮式滴灌帶采用迷宮式流道，具有一定的壓力補償作用，因此在一定范圍內的地形起伏對灌水均勻度影響較小。

（2）主因素效應多重比較。坡度對單翼迷宮式滴灌帶灌水均勻度的影響不顯著，故不作多重比較分析，對本試驗中的進水口壓力和鋪設長度2 個因素進行多重比較分析。由表7可知，3種型號單翼迷宮式滴灌帶在進水口壓力對灌水均勻度的影響中，均以B2 處理對灌水均勻度影響最大；在滴灌帶鋪設長度對灌水均勻度的影響中，均以C1 處理對灌水均勻度的影響最大。由多重比較可知，灌水均勻度并不是隨進水口壓力增加而單調遞增，而是在壓力適中條件下達到最高。這是因為滴灌帶內的水流狀態隨進水口壓力變化而發生改變，從而使滴頭流量發生變化，最終導致滴灌帶灌水均勻度發生變化；隨著單翼迷宮式滴灌帶鋪設長度的增加，滴灌帶滴頭處的壓力呈下降趨勢，從而導致灌水均勻度發生改變。

表7 方差分析及多重比較Tab.7 Analysis of variance and multiple comparisons

2.4 回歸模型的建立

通過對單翼迷宮式滴灌帶灌水均勻度試驗數據的整理與分析，初步建立一個Cu=f(L,I,P)的函數模型（其中，Cu表示滴灌的灌水均勻度，I為鋪設坡度，P表示滴灌帶進水口壓力，L為滴灌帶鋪設長度）。

采用多元線性回歸模型，具體模型如下：

式中：Y為預測值；xi為關鍵參數；α為常數項；δ為殘差；βi為線性回歸系數。

進而使用SPSS 23.0 線性回歸分析進行計算，并嘗試建立相關線性模型。由表8可知，H1、H2和H3型滴灌帶回歸模型的決定系數分別為0.638、0.662 和0.480，顯著性分別為0.139、0.117 和0.313。說明由SPSS 建立的3 個線性模型均不顯著，且擬合精度較低，可能存在非線性關系。

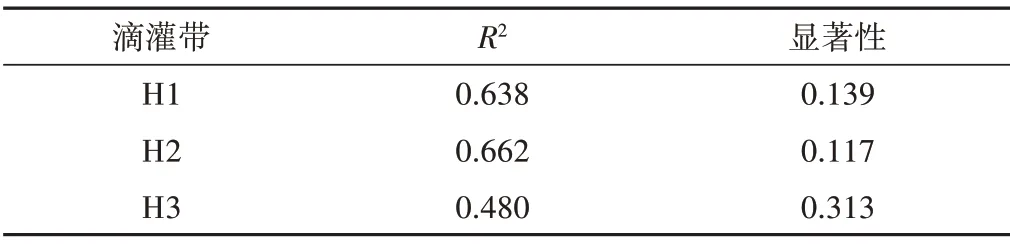
表8 回歸方差分析Tab.8 Regression analysis of variance

2.5 基于PPR 無假定建模技術的滴灌帶灌水均勻度模型

2.5.1 PPR原理

投影尋蹤回歸(PPR)[20]是一種用來分析多維數據的方法，尤其是非線性和非正態的數據，文獻[21，22]中有詳細介紹，在此不再贅述。近年來，投影尋蹤理論這一分析高維數據的方法多應用于水利工程和農業工程等領域[23，24]，但將投影尋蹤建模方法用于滴灌帶灌水均勻度影響因素的研究鮮有報道。為此，本文以不同灌溉條件下單翼迷宮式滴灌帶灌水均勻度的數據為基礎，采用投影尋蹤建模方法對清水條件下影響單翼迷宮式滴灌帶灌水均勻度的參數進行反演分析，為探究單翼迷宮式滴灌帶灌水均勻度影響因素及影響程度提供高精度參數并建立數學模型。

設（X，Y）是一組隨機變量，Y=(y1，y2，…，yQ)是Q維隨機向量，X=(x1，x2，…，xP)是P維隨機向量，PPR 無假定建模即根據（X，Y）的n次觀察結果（Xn，Yn），其中n=1，2，3，…，n，采用若干嶺函數加權和形式逼近回歸函數F（x）=E(Y|X=x)：

式中：fm為第m個嶺函數，Ef= 0，Ef2m= 1；M為嶺函數上限個數；βm表示嶺函數的貢獻權重系數；yi為第i個因變量，1≤i≤Q；為第i個因變量n次觀測結果的均值；xj為第j個自變量，1≤j≤p；αmj為第j個方向的第m個分量，

投影尋蹤回歸（PPR）是采用計算機程序對上式參數進行逐步尋優的過程，估算出fm，確定αmj、βm的最優組合，使之滿足如下極小化準則：

式中：Mu為嶺函數最優個數；Wi為應變量的權重系數。

2.5.2 基于PPR非線性回歸模型輸出結果與分析

由于3 種不同流量的單翼迷宮式滴灌帶具有相似性質且PPR 建模分析數據量較大，所以PPR 建模只選用H1 型滴灌帶作為研究對象。在建立模型時，除了表2中9 組建模樣本外，還包括9組預留檢驗樣本（見表9）。

表9 H1預留檢測樣本Tab.9 H1 Reserve test samples

依照上述步驟，采用PPR 軟件分別對9 組H1 單翼迷宮式滴灌帶建模樣本和9組預留檢驗樣本進行計算分析。計算時模型投影參數分別為：Span＝0.5，M＝5，Mu＝3。其中：Span為光滑系數，決定模型的靈敏度，Span越小模型越靈敏，其取值范圍為0＜Span＜1，采用“精度一致檢驗法”準則來確定本模型Span的最終取值為0.5；M和Mu決定模型尋找數據內在結構的精細程度。最終3 種型號滴灌帶建模參數均為：N=9，P=3，Q=1，M=5，Mu=3。通過PPR 建模，得到H1 型號滴灌帶灌水均勻度的嶺函數權重系數β和投影方向α依次如式（8）和式（9）所示，分別將各考核指標嶺函數相應的權重系數和投影方向的向量式代入式（7）中即可得到最終的計算模型。

2.5.3 模型精度分析

分析時，取“還原擬合值”與實測值的相對誤差｜δ｜≤5%作為判定合格率的標準。根據上述建模過程及準則，計算建模樣本和預留檢驗樣本的“還原擬合值”，并將其與實測值進行比較，結果見圖2。建模樣本為圖2（a），預留檢測樣本為圖2（b），圖2虛線為2 者相對誤差δ的閾值線。從圖2可以看出：各樣本的“還原擬合值”與實測值相差均較小，9組建模樣本數據的合格率為100%，最大相對誤差為0.14%；9組預留檢驗樣本的合格率為100%，最大相對誤差為1.06%。由此可知建立的PPR數學模型具有良好的穩定性和較高的精度。

同時，建模過程中還計算出了鋪設坡度、進水口壓力、鋪設長度對單翼迷宮式滴灌帶灌水均勻度的影響權重，結果見表10。由表10 可知，影響單翼迷宮式滴灌帶因素按權重大小排序為：進水口壓力＞鋪設長度＞鋪設坡度。與前文極差、方差分析中各因素對單翼迷宮式式滴灌帶灌水均勻度影響的顯著性大小排序一致，可看出由PPR 建立的數學模型分析結果不僅與極差、方差分析結果有較好的一致性，而且在預測試驗結果這一方面具有很高精確性，這可以很大程度上解決滴灌帶試驗周期長、試驗工程量大等問題。