類氫原子核質量對電子狀態的影響*

劉兆斌 李凱 曾天海 王鋒 宋新兵 邵彬 鄒健

(北京理工大學物理學院, 北京 100081)

在孤立的兩體復合系統中, 討論其中一體的變化如何影響另一體的狀態, 有助于了解單粒子混合態與純態的關系.本文討論5 個孤立的一維類氫原子模型系統, 原子核的質量互不相同.這5 個兩體(電子與原子核)復合系統的相對運動狀態都處于糾纏態, 其中電子狀態都用約化密度矩陣表示的混合態描述.在原子核質量趨近無窮大的一維氫原子模型中, 電子處于純態.為比較這里的純態和混合態, 在位置表象中計算了這些混合態的純度、它們分別與純態的保真度、以及所有這些態的相干性.研究表明, 原子核的質量越大, 純度和保真度越接近1, 混合態的相干性與純態的也越接近.這樣的純態及其相干性可以是這種混合態及其相干性的近似, 并與原子核及庫侖相互作用有關.

1 引 言

單個粒子可以處于純態或混合態.在量子信息傳輸中, 單粒子的初始純態一般會變為混合態.很難制備單粒子純態, 得到的一般是混合態.如何得到接近純態的混合態是個有意義的問題.在孤立的氫原子模型中, 假設原子核質量趨近無窮大, 則其電子處于純態.但考慮氫原子核的質量, 那么, 核與電子處于糾纏態[1,2](即不能寫成原子核狀態與電子態的直積態), 電子處于混合態.對于不同的類氫原子, 其核質量不同, 它們的電子混合態也會不同.核質量越大, 電子混合態自然越接近相應的純態.本文定量討論混合態與純態是如何接近的.

討論5 個一維類氫原子系統, 它們具有相同的電子和庫侖相互作用勢能, 而原子核的質量不同.假設前兩個原子的核質量與電子的比為10 和100,后三個是氕、氘和氚原子, 質量比約為1836, 2 ×1836 和3 × 1836.它們均可以看成兩體復合系統,這些兩體復合系統都處于糾纏態, 可以用密度矩陣表示.對密度矩陣的一部分求跡, 得到的約化密度矩陣[3,4]表示另一部分的狀態為混合態.在假設的原子核質量為無窮大的一維氫原子中, 電子處于純態.把這5 種情形的電子混合態及其相干性與純態及其相干性進行比較.比較的方式是用純度[5]、保真度[6?10]和相干性[11?22]進行定量計算.根據定義, 純度定量表征混合態中的純態“含量”.純度越高, 越接近純態; 純度為1 的即為純態.保真度可以用來定量比較兩個量子態的接近程度.若值為1,則兩個態相同.量子態的相干性與選取的表象有關, 若在所選的表象中為本征態, 則沒有相干性;純態的相干性表征干涉的對比度; 而對于一個混合態, 相干性則表征了所有純態成分的干涉或相干的大小總和.

本文第2 節引用一維類氫原子的兩體模型, 計算第一激發態及其與第二激發態的疊加態中的電子混合態密度矩陣.第3 節計算這些混合態的純度、與相應純態之間的保真度、以及用l1norm 定量的混合態和純態的相干性.

2 模 型

這里采用簡單的孤立一維氫原子模型[1,23,24].用薛定諤方程求解這樣的兩體問題, 可以分成質心運動和相對運動兩部分.質心運動相當于自由粒子運動.文獻[3]指出, 自由粒子的初始能量可以為零.因此, 設質心不動, 為坐標原點.只需考慮相對運動.對于原子核質量趨近無窮大的一維氫原子,文獻[23,24]給出了其定態薛定諤方程的波函數偶宇稱和奇宇稱的表達式:

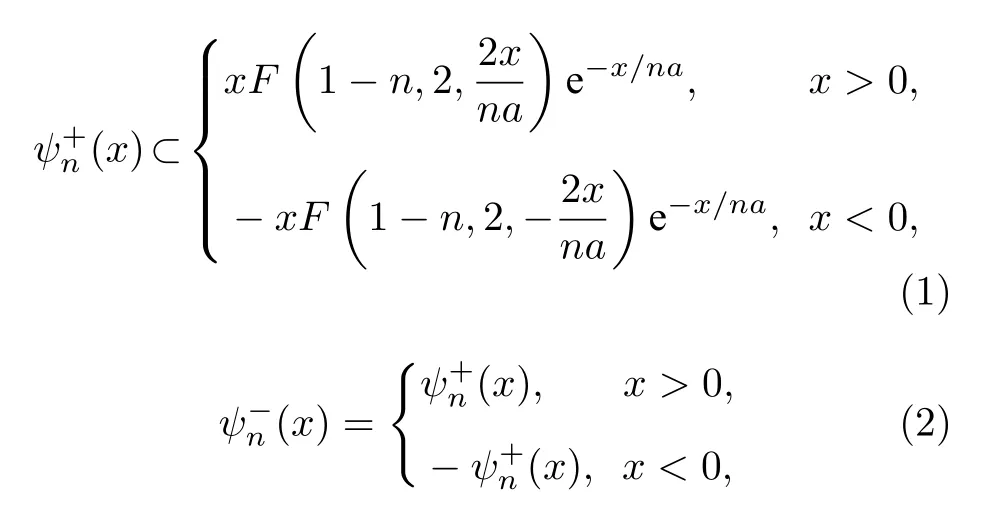
其中F為合流超幾何函數,a是玻爾半徑,和都是實函數.

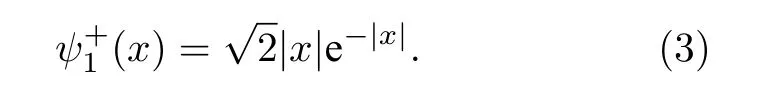
歸一化的第一與第二激發態偶宇稱波函數的疊加態可寫成

當考慮原子核的質量時, 第一激發態偶宇稱波函數變為

第一與第二激發態偶宇稱波函數的疊加態變為

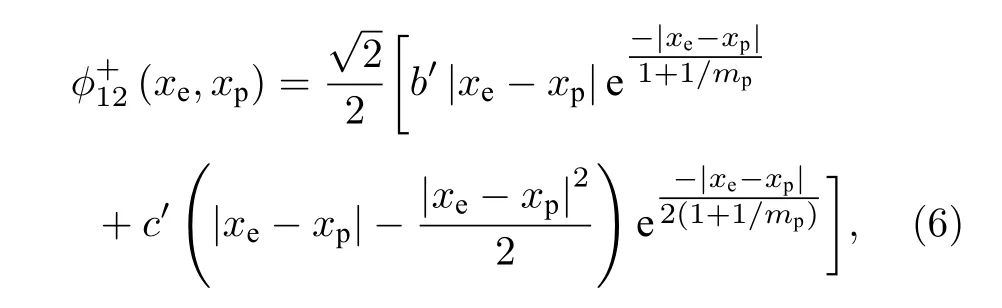
其中xe和xp分別是電子和原子核的位置坐標;mp是原子核質量;b′和c′是相應第一和第二激發態偶宇稱波函數的歸一化常數, 數值大小隨所取的原子核質量的大小不同而不同, 并能通過求全空間概率為1 得到具體數值.和都是實函數.相應的密度矩陣為:和假設電子為粒子1, 原子核為粒子2.對粒子2 部分求跡可得到電子的約化密度矩陣表示電子的混合態.在位置表象中, 位置有連續本征值譜[4], 相應的約化密度矩陣元分別表示為

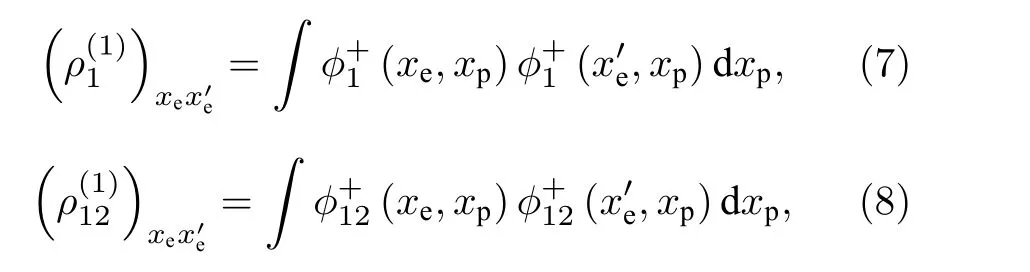
其中xe和分別表示約化密度矩陣的行和列.

3 純度、保真度和相干性計算

3.1 純度的計算

混合態的純度的一種定義[5]為

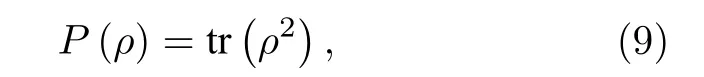
在位置表象中, 求跡寫成積分.對于約化密度矩陣其純度計算公式可分別表示為

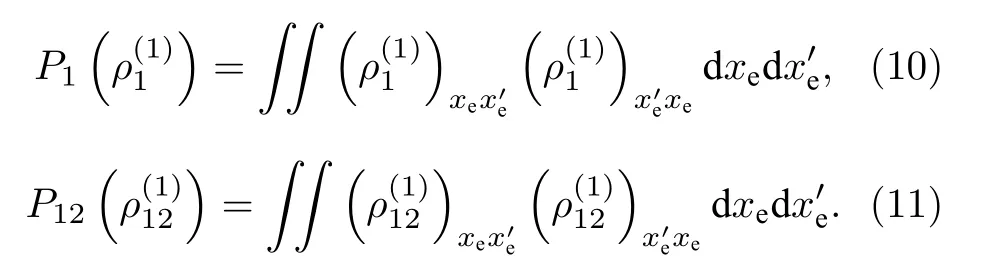
按照上述 ? =1 ,e=1 ,me=1 的設定, 當積分區間取 [?20,20] 范圍內時, 第一激發態和疊加態偶宇稱波函數所表示的概率非常接近1, 所以電子的積分區間取 [?20,20].根據兩體問題的運動關系, 相應的原子核的積分區間取為其中mp是原子核的質量.

考慮5 個一維類氫原子系統， 分別計算了原子核質量取不同值時，電子混合態的純度的變化趨勢, 即的變化趨勢.

圖1 為純度變化趨勢圖, 可以看出, 原子核的質量越大, 電子混合態的純度越高, 并非常接近1.對于氕、氘和氚原子, 電子混合態都近似于某個純態.反之, 說明一個純態是由混合態近似而來的.

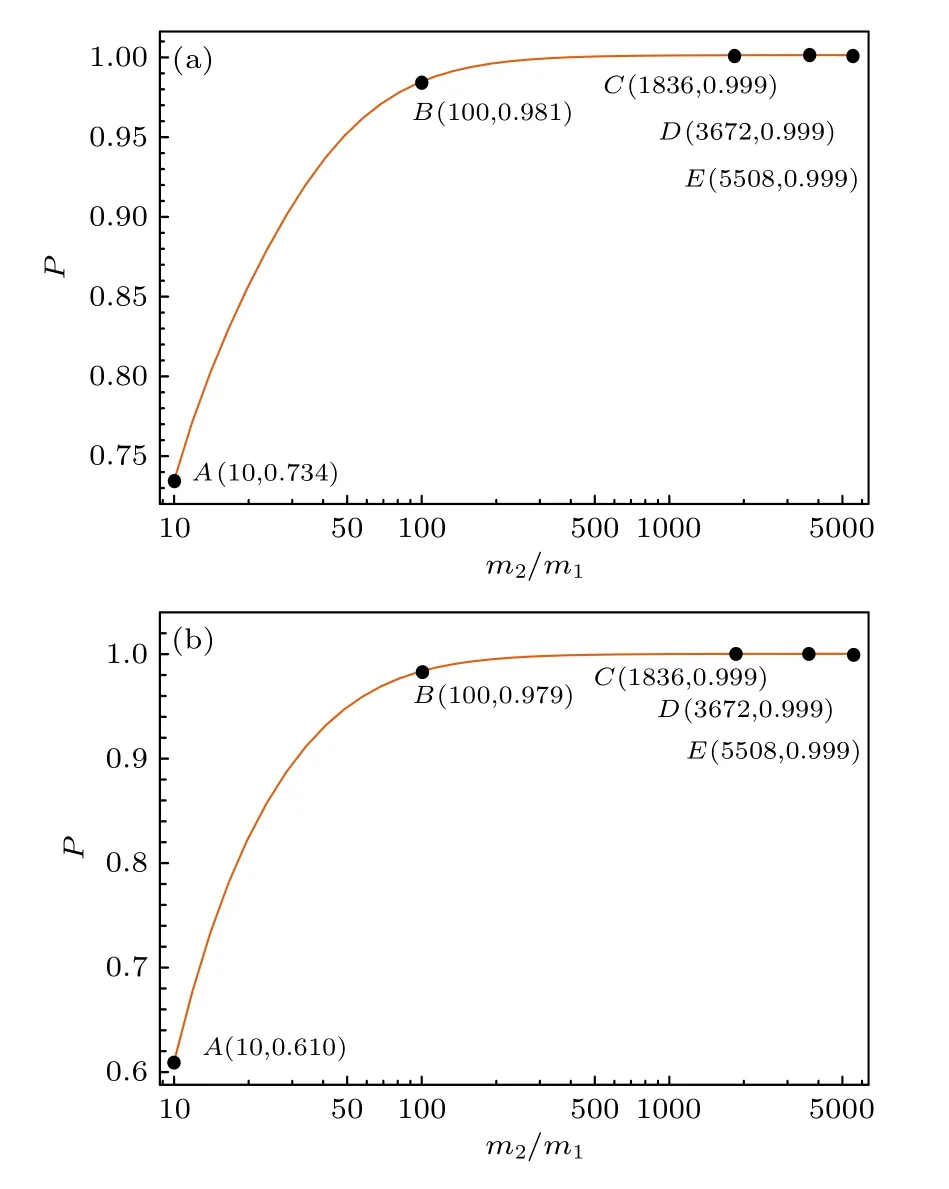
圖1 純度變化趨勢圖, 橫坐標表示原子核質量和電子質量之比 (a) 第一激發態; (b) 疊加態Fig.1.Purity vs.the ratio of mass between nucleus and electron: (a) The first excited state; (b) the superposition of the first and the second excited states.

3.2 保真度的計算

混合態與純態之間的保真度定義[9]為

兩個保真度變化趨勢如圖2 所示.

從圖2 可以看出, 原子核的質量越大, 保真度越大, 電子混合態與相應的純態也越接近.在氕、氘和氚原子情形, 保真度都接近1, 說明電子混合態都近似于純態.反之, 說明這兩個純態都是由相應混合態近似而來的.

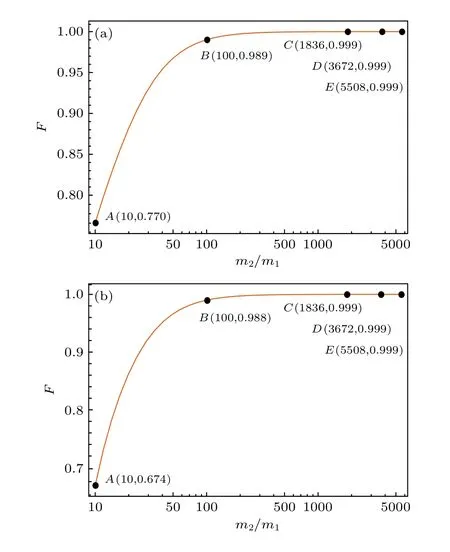
圖2 保真度變化趨勢圖, 橫坐標表示原子核質量和電子質量之比 (a) 第一激發態; (b) 疊加態Fig.2.Fidelity vs.the ratio of mass between nucleus and electron: (a) the first excited state; (b) the superposition of the first and the second excited states.

3.3 相干性的計算

量子態的相干性是相對特定表象而言的.在能量表象中, 這里的電子第一激發態是能量本征態,沒有相干性.但在位置表象中, 第一激發態是位置本征態的疊加態, 是有相干性的.第一與第二激發態的疊加態在這兩個表象中, 都有相干性.這里也采用位置表象.量子態l1norm 相干性定義[13]為:在采用位置表象后, 求和改成積分的形式

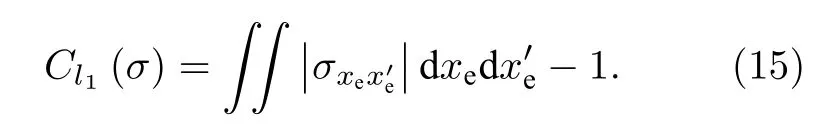
從圖3 可以看出, 原子核的質量越大, 電子混合態的相干性與相應純態的相干性越接近.也說明氕、氘和氚原子中, 電子混合態的相干性都近似于相應純態的相干性.

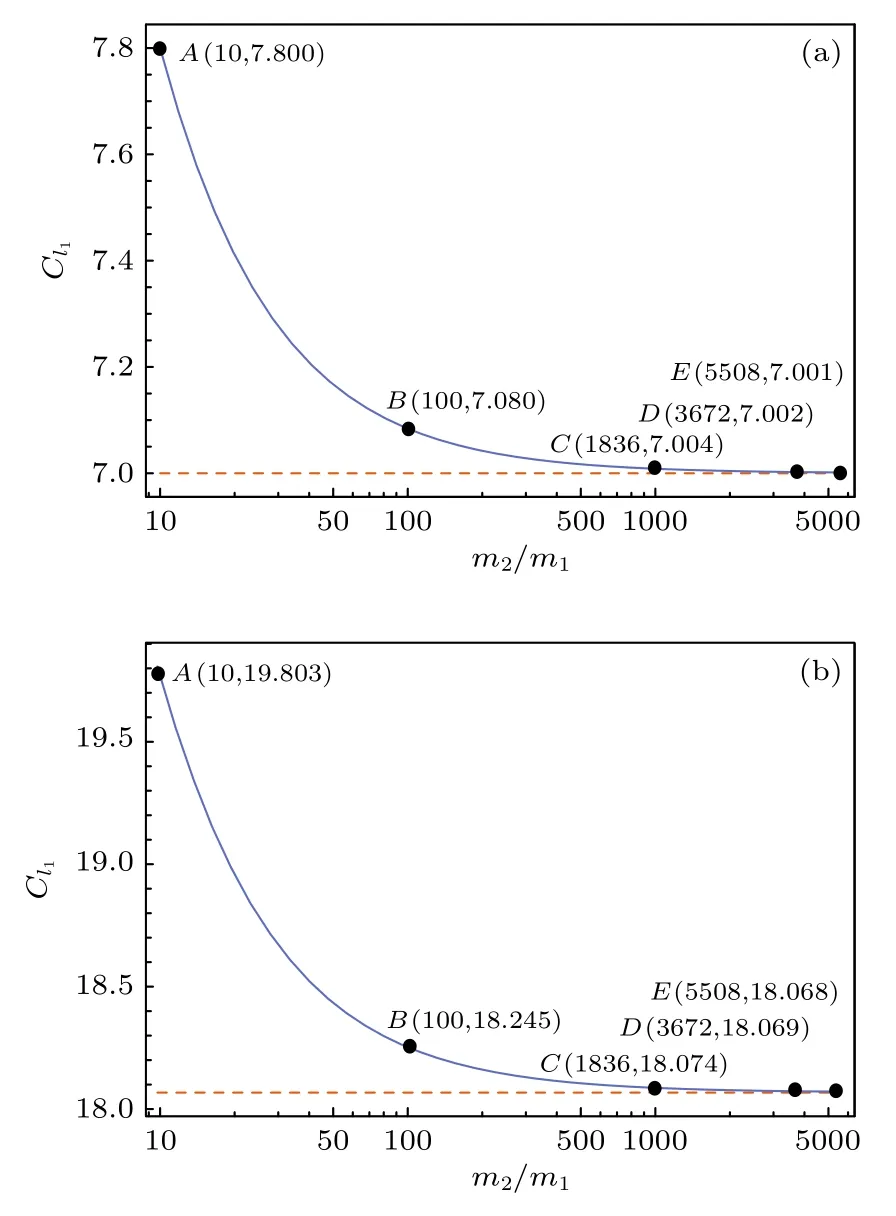
圖3 相干性變化趨勢圖, 橫坐標表示原子核質量和電子質量之比 (a)第一激發態; (b)疊加態Fig.3.Coherence vs.the ratio of mass between nucleus and electron: (a) The first excited state; (b) the superposition of the first and the second excited states.

3.4 討 論

與純度和保真度不同的是, 這里得到的電子混合態的相干性不是隨原子核質量的增大而增大, 而是相反.這可以做如下解釋: 在特定表象中, 若純態是本征態, 則沒有相干性; 而混合態的成分中,有不同本征態的相干疊加態, 則相干性不為零.例如, 某一表象有三個本征態基矢{φ1, φ2, φ3}, 若純態是其中任一本征態, 則相干性為零; 而混合態中出現純態的概率為1/3, 出現純態的概率為2/3, 則相干性不為零.說明混合態的相干性可以大于純態的相干性.

雖然相干性變化規律與保真度不同, 但仍然說明這兩個純態的相干性都是由相應混合態近似而來的.這里的電子混合態及其相干性, 都是與原子核及它們的庫侖相互作用勢能有關的.這是因為這樣的兩體復合系統的哈密頓量含有原子核的動能算符和庫侖相互作用勢能算符, 電子與原子核的糾纏態就與原子核質量和庫侖相互作用有關.若原子核質量很大, 它就近似不動或它的狀態近似不變,庫侖相互作用勢能也近似為電子的外場庫侖勢能.換一個角度看, 原子核與電子的糾纏態近似為核的不變狀態與電子態的直積態[25?30].這樣, 電子的純態就是近似的, 這個純態及其相干性就與原子核及它們的庫侖相互作用勢能有關.

這個特例有可能推廣到其它孤立的兩體復合系統中進行定量計算.其一體保持為微觀體不變,相互作用勢能也不變, 而另一體由微觀體換成宏觀體.那么, 微觀體在宏觀體的勢場中運動, 其狀態近似為純態, 并在一些表象中顯示相干性.因此,這個純態及其相干性與宏觀體有關, 并與相互作用勢能(即近似的外場)有關.

4 結 論

本文利用純度、保真度和相干性, 對一維類氫原子中的電子狀態隨核質量的變化進行了定量計算.結果表明, 一維類氫原子核質量趨近無窮大的電子純態及其相干性, 可以由一維類氫原子中電子的混合態及其相干性近似而來.這種電子混合態及其相干性與原子核及它們的庫侖相互作用勢能有關, 因而, 電子的這種純態及其相干性也是如此.說明存在單粒子的一些純態及其相干性是混合態及其相干性的近似, 并且這些態及其相干性與其他物體及相互作用有關.