橫向非均勻介質多道瑞雷波頻散曲線正演

胡書凡， 趙永輝* ， 吳健生2,， 葛雙成

1 同濟大學海洋與地球科學學院， 上海 200092 2 九三學社上海市委員會， 上海 200041 3 浙江水利水電學院， 杭州 310018

0 引言

瑞雷波是由縱波和橫波垂直分量在自由表面發生相長干涉而形成的一種沿自由表面傳播的地震波.在垂向非均勻介質中，瑞雷波具有幾何頻散特性，即不同頻率分量以不同的相速度傳播，進而可用來探測地下介質的速度結構信息，其應用領域包括淺地表地球物理(曾求等，2020；宋政宏等，2020；林融冰等，2020)、勘探地球物理(孟小紅和郭良輝，2007；吳曲波等，2019)及區域與全球地震學(顧勤平等，2020；付媛媛和肖卓，2020)等.在淺地表面波勘探中，早期采用的面波譜分析法(Spectral Analysis of Surface Waves, SASW)通過測量兩道接收信號的相位差來獲取頻散曲線(Nazarian et al.，1986)，但其計算結果存在易受隨機噪聲、體波以及多模式疊加等影響的問題(Neducza，2007；Hashemi et al.，2019).而之后發展的面波多道分析法(Multichannel Analysis of Surface Waves, MASW)將接收到的時空域多道面波信號變換到另一個域中以此來構建頻散圖像(Park et al.，1999；Xia et al.，1999)，根據面波的強能量特征可從此圖像中提取得到高質量的頻散數據(Socco et al.，2010)，常用的變換方法有：頻率-波數變換(Gabriels et al.，1987；Rix et al.，2002)、傾斜疊加變換(McMechan and Yedlin，1981；Xia et al.，2007)以及相移法(Park et al.，1998)等.當前，面波多道分析方法以其非侵入性、無損、高效及經濟的特點而越來越受到學術界的重視(夏江海等，2015).

瑞雷波頻散曲線的正演是其反演的基礎，并可為實際工作調查的設計提供理論指導依據.當前，面波多道分析法中采用的理論頻散曲線計算方法大多基于水平層狀模型假設，主要有Thomson-Haskell法(Thomson，1950；Haskell，1953)、Schwab-Knopoff法(Schwab and Knopoff，1970，1972)、δ矩陣法(Watson，1970；Buchen and Ben-Hador；1996)、Abo-Zena法(Abo-Zena，1979)、反射透射系數法(Kennett and Kerry，1979)以及廣義反射透射系數法(Chen，1993；何耀鋒等，2006)等.上述方法通過對頻散方程進行搜根可快速實現瑞雷波理論相速度的計算，但實際淺地表介質中往往呈現較明顯的橫向不均勻性，接收排列下方是否能用水平層狀模型來表達還有待商榷.而基于波動方程的全波場模擬理論上可考慮瑞雷波在任意橫向變化介質中的傳播，模擬過程通常采用有限元(劉雪明等；2009)、有限差分(周竹生等，2007；袁士川等；2018)等數值計算方法來實現，其中又以交錯網格有限差分算法(Virieux，1986)應用最為廣泛.在交錯網格有限差分算法中，自由表面邊界的處理將對瑞雷波模擬精度產生較大的影響，早期常采用的真空近似法(Boore，1972)存在數值穩定性差和計算精度低的問題(Graves，1996).之后，通過許多學者的研究，分別提出了應力鏡像法(Levander，1988)、橫向各向同性介質替換法(Mittet，2002)、聲學-彈性邊界近似法(Xu et al.，2007)和改進的真空處理公式(Zeng et al.，2012)等自由表面邊界的處理方法，有效地提高了瑞雷波的模擬精度.在模擬得到全波場記錄后，可與實際處理一樣采用面波多道分析法來提取瑞雷波頻散曲線.然而，在實際正演模擬中往往需要對多組模型及其參數變化的影響進行分析，由于計算精度的要求以及穩定性條件的限制導致該類方法需要較長的計算時間.

鑒于現有頻散曲線計算方法受限于水平層狀模型假設或全波場模擬計算量較大等問題，本文從面波多道分析法中聚束分析的計算公式入手，通過推導振幅歸一化后聚束分析輸出功率譜中相速度與局部相速度之間的關系，采用類似于從頻散圖像中估計多道瑞雷波相速度的方式，利用黃金分割極值搜索算法求得理論相速度值，以實現橫向非均勻介質中多道瑞雷波頻散曲線的快速正演.并針對兩類典型的橫向不均勻介質模型，分析了局部頻散曲線、平均頻散曲線以及本文方法計算得到的理論頻散曲線與二維彈性波場模擬分析得到的頻散曲線之間的差異.

1 振幅歸一化聚束分析

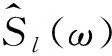
(1)

其中，j2=-1；ω為角頻率，單位為rad/s；k為波數，單位為rad/m；wl為每道的權重.

上式也可寫成矩陣形式，表示為

Z(ω,k)=eH(k)WS(ω),

(2)

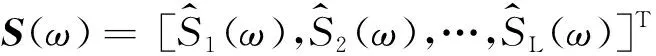
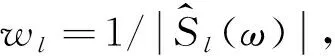
在頻散分析過程中，通常計算的是聚束分析的輸出功率譜(Rix et al.，2002；Zywicki and Rix，2005)，表示為

P(ω,k)=Z(ω,k)Z(ω,k)H

=eH(k)WS(ω)SH(ω)WHe(k)

=eH(k)WR(ω)WHe(k),

(3)

其中，R(ω)為空間譜相關矩陣，表示為

(4)

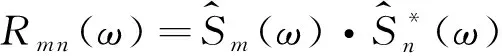
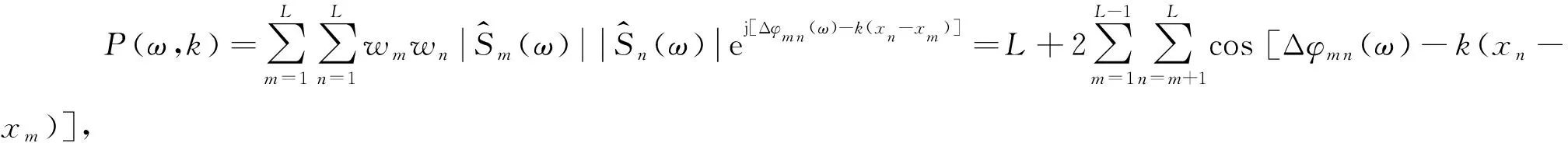
(5)

其中，Δφm n(ω)為第m與第n道之間的相位差.由式(3)可知，利用式(5)進行頻散分析得到的相速度與利用相移法估計得到的相速度仍然是一致的，只是該式計算的是功率譜，而相移法生成的頻散圖像所表征的是幅度譜.

2 多道瑞雷波頻散曲線正演

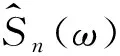
(6)

其中，dm n=xn-xm為兩道之間的距離；km n(ω)為兩道之間的空間波數，確定了瑞雷波在兩接收點之間的傳播；Am n(ω)為與頻率相關的衰減函數.

在正問題中可將地下模型離散為一系列的網格單元，網格單元的厚度可根據需求設置相同或不同(如圖1a所示)，若只考慮彈性介質，則每個網格單元的彈性參數由橫波速度、縱波速度以及密度表征.在此模型離散方式下，(6)式可表示為如下形式

(7)

其中，kq(ω)為局部空間波數，由m與n道之間第q列網格單元的彈性參數確定；Δxq為m與n道之間第q列網格單元的寬度.

根據式(7)，第m與第n道之間的相位差可表示為

(8)

將(8)式代入(5)式，并根據關系v=ω/k，可得到振幅歸一化聚束分析輸出功率譜中相速度與局部相速度之間的關系，表示為

(9)

其中，vq(ω)為局部相速度.

在實際多道瑞雷波數據的頻散分析過程中，頻散曲線通常是根據頻散圖像中的譜峰值來確定的.同樣地，多道瑞雷波數據的理論頻散曲線也可通過求取式(9)的局部極大值來求得，其具體實現方法：

(1)利用傳遞矩陣算法求得由每一列模型網格單元構成的層狀模型的局部相速度vq(ω).

(2)將局部相速度vq(ω)轉換為局部空間波數kq(ω)，并根據(8)式計算每接收對之間的相位差Δφm n(ω).

(3)利用黃金分割極值搜索算法求得式(9)的局部極大值v(ω)，計算完所有頻率點后即可得到多道瑞雷波數據的理論頻散曲線.

正演算法流程如圖1所示.對于復雜地質模型式(9)可能存在多個局部極大值，因此在極值搜索過程中應充分考慮頻散曲線的連續性，即將上一個頻點的相速度值作為初值進行搜索，從而得到一條與實際頻散曲線相匹配的理論頻散曲線.

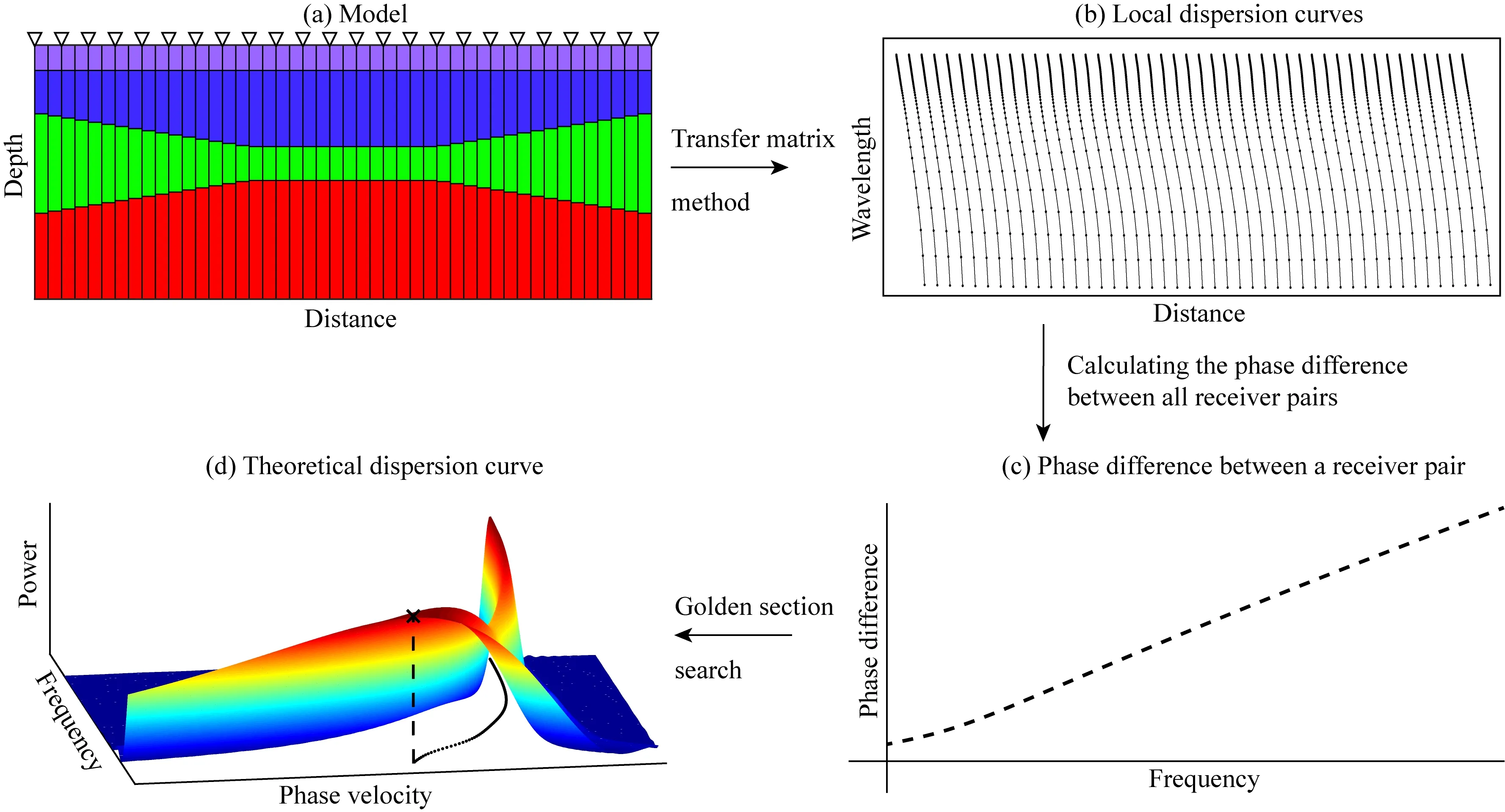
圖1 正演算法流程圖(a) 模型網格剖分示例，黑色表示接收點位置； (b) 局部頻散曲線； (c) 接收對之間的相位差； (d) 振幅歸一化聚束分析的輸出功率譜，黑色點線為通過黃金分割極值搜索得到的多道瑞雷波頻散曲線.Fig.1 Workflow for the forward algorithm(a) Example of model discretization. The black indicates the position of receivers; (b) Local dispersion curves; (c) Phase difference between a receiver pair; (d) Output power of the amplitude-normalized beamforming. The black dotted line represents the multichannel Rayleigh wave dispersion curve obtained by the Golden Section search.

3 理論模型試驗

為驗證本文所提出的基于聚束分析的多道瑞雷波頻散曲線正演算法的可靠性，對典型的橫向不均勻介質模型(斷層模型、含低速異常模型)進行了試驗.首先通過二維交錯網格時間域有限差分算法(Virieux，1986)，對各向同性彈性模型進行全波場模擬.全波場數值模擬中采用時間二階、空間十二階的差分精度，自由邊界條件采用應力鏡像法(Levander，1988)進行處理；模型大小為60 m(寬)×15 m(深)，橫縱向網格剖分為0.1 m×0.1 m；激發震源采用中心頻率為20 Hz的雷克子波，時間采樣間隔取0.25 ms；接收排列共48道，最小偏移距10 m，道間距1 m.在得到了瑞雷波的波形記錄后，采用式(5)對多道瑞雷波數據進行頻散分析并根據譜峰值提取相應的頻散曲線.之后，采用基于聚束分析的多道瑞雷波頻散曲線正演算法對相同模型進行計算得到理論頻散曲線，并分析該理論頻散曲線與波場模擬分析得到的頻散曲線之間的誤差.

由于在一定偏移距范圍內瑞雷波以柱面波方式傳播且此范圍內體波能量較強，從而對頻散分析造成影響并導致低頻分量的相速度值被低估或高估，又稱之為近場效應(Zywicki，1999)，因此本文采用歸一化排列中心距(Normalized Array Center Distance，NACD)和歸一化瑞雷波速度(Normalized Rayleigh Wave Velocity，NRWV)來進行誤差分析(Yoon and Rix，2009)，其計算公式分別為

(10)

(11)

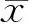
3.1 斷層模型

如圖2a所示，在該模型中間區域存在地層錯斷，模型中泊松比為常數0.333，每層密度均為1900 kg·m-3，在橫向大于40 m的區域內地層橫波速度由上到下依次為100、120、170 m·s-1和270 m·s-1.圖中紅色圓圈為激發震源位置，黑色三角形為接收點位置，黑色虛線代表接收排列中點.圖2b為利用全波場模擬得到的共炮點道集，可以看出在偏移距為20 m左右處瑞雷波記錄的視速度發生了明顯變化，意味著地下存在較強的橫向不均勻性.

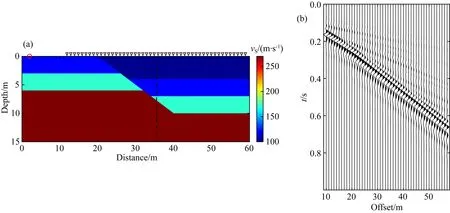
圖2 斷層模型及相應的單炮記錄(a) 斷層模型，紅色○和黑色分別表示激發震源和接收點的位置，黑色虛線代表接收排列中點； (b) 模擬的共炮點道集.Fig.2 Fault model and the corresponding single-shot record(a) Fault model. The red ○ and black represent the positions of source and receivers, respectively; (b) The simulated common-shot gather.

圖3a為利用式(9)計算得到的振幅歸一化聚束分析的理論輸出功率譜, 圖中黑色虛線代表波數k=2π/L，其中L為接收排列長度.在模型離散過程中，每個網格單元的寬度固定為0.1 m、厚度根據模型設定.需要說明的是，在理論頻散曲線的正演過程中并不需要像生成頻散圖像那樣計算每個相速度值對應的理論功率譜，而只需進行極大值搜索即可.由圖可見，在橫向不均勻模型中理論功率譜將存在多個局部極大值，而利用考慮頻散曲線連續性的策略可較好地搜索得到一條光滑變化的理論頻散曲線(圖3a中白色點線).圖3b為利用式(5)對模擬單炮記錄進行波場變換得到的頻散圖像，圖中黑色虛線代表波數k=2π/L.相較于圖3a，此頻散圖像中的能量分布在一定程度上受到了體波及散射面波的影響.在頻率小于5 Hz的范圍內，由于低頻分量的缺失以及泄露誤差的影響，已難以準確地獲取瑞雷波相速度，同時在高頻段相速度趨于常速度值，因此在接下來的對比中只對5～50 Hz頻段范圍內的分量進行分析，從頻散圖像中提取的頻散曲線如圖3b中的黑色點線所示.采用基于聚束分析的多道瑞雷波頻散曲線正演算法計算得到的理論相速度值如圖3b中的白色點劃線所示，可以看出在整個頻段范圍內該理論頻散曲線與提取的頻散曲線吻合較好，只是在5～6 Hz頻段內相速度值要低于提取值，這主要是由于低頻瑞雷波不發育以及近場效應所導致的，理論頻散曲線與提取頻散曲線之間的均方根誤差為4.02 m·s-1，大于6 Hz頻段內的均方根誤差為0.94 m·s-1.接收排列中點處的局部頻散曲線如圖3b中的黑色點劃線所示，在所有頻段內局部頻散曲線的相速度值都要低于提取得到的相速度值，兩者之間的均方根誤差為6.83 m·s-1，大于6 Hz頻段內的均方根誤差為5.54 m·s-1，說明當地下存在較強的橫向不均勻性時利用面波多道分析法提取的頻散曲線并不滿足中點假設，將提取得到的頻散曲線置于排列中點會給之后的反演解釋帶入較大的誤差.接收排列下方所有局部頻散曲線的平均值如圖3b中的藍色點劃線所示，在大于6 Hz頻段范圍內平均相速度值皆高于提取得到的相速度值，兩者之間的均方根誤差為6.96 m·s-1，大于6 Hz頻段內的均方根誤差為6.16 m·s-1，說明面波多道分析法得到的頻散曲線并不是排列下方局部頻散曲線的簡單算術平均.

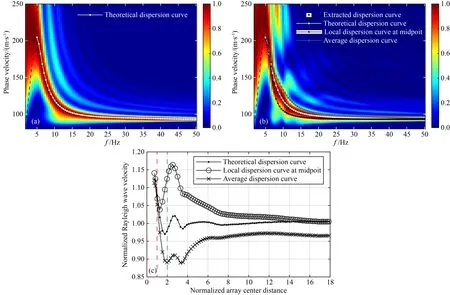
圖3 斷層模型頻散分析結果(a) 基于振幅歸一化聚束分析得到的理論功率譜，白色點線為極值搜索得到的理論多道瑞雷波頻散曲線，黑色虛線代表波數k=2π/L； (b) 模擬的單炮記錄進行波場變換得到的頻散圖像，黑色點線為提取得到的頻散曲線，白色點劃線為正演得到的理論頻散曲線，黑色點劃線為排列中點處的局部頻散曲線，藍色點劃線為排列下方的平均頻散曲線，黑色虛線代表波數k=2π/L； (c) NACD-NRWV曲線圖，黑色點劃線、○標注線和×標注線分別為以理論相速度、局部相速度、以及平均相速度作為參考速度計算得到.Fig.3 Results of dispersion analysis for fault model(a) Theoretical out power of the amplitude-normalized beamforming. The white dotted line represents the multichannel Rayleigh wave dispersion curve obtained by the local maximum search. The black dashed line indicates wavenumber k=2π/L; (b) Dispersion image generated from the simulated common-shot gather. The black dotted line indicates the extracted dispersion curve, the white dot-solid line represents the theoretical dispersion curve, the black dot-solid line is the local dispersion curve at the midpoint of receiver array, and the blue dot-solid line depicts the average phase velocity beneath the entire receiver array. The black dashed line indicates wavenumber k=2π/L; (c) The plot of normalized Rayleigh wave velocity versus normalized array center distance. The black dot-solid line, the ○ marked line, and the × marked line are calculated by the theoretical phase velocity, local phase velocity, and average phase velocity.

圖3c為將理論頻散曲線、局部頻散曲線和平均頻散曲線作為參考相速度計算得到的歸一化排列中心距-歸一化瑞雷波速度曲線圖(NACD-NRWV曲線圖).根據水平層狀模型中近場效應的研究(Yoon and Rix，2009；Bodet et al.，2009；Roy and Jakka，2017)，當地層中橫波速度呈速度遞增型時，歸一化排列中心距大于1的范圍內相對誤差小于10%；而對于所有類型地層，歸一化排列中心距大于2的范圍內相對誤差小于5%.利用理論頻散曲線作為參考值得到的曲線如圖3c中的黑色點劃線所示，在歸一化排列中心距大于1的范圍內最大相對誤差為7.8%，在歸一化排列中心距大于2的范圍內最大相對誤差為2.1%，這與水平層狀模型中的研究結果一致，進一步說明了本文正演方法的可靠性.利用排列中心點處局部頻散曲線作為參考值得到的曲線如圖3c中的圓號標注線所示，在歸一化排列中心距大于1和大于2的范圍內最大相對誤差皆為16.4%，可知在此情況下排列中點假設并不成立.利用排列下方局部頻散曲線的平均值作為參考相速度得到的曲線如圖3c中的叉號標注線所示，在歸一化排列中心距大于1和大于2的范圍內最大相對誤差皆為11.0%，相比于理論頻散曲線的結果誤差值較大.

本文所有算法的計算部分代碼都是在Intel Core i3-4150處理器、Windows操作系統下利用Intel Fortran編譯器進行編譯執行的.對于二維彈性波時間域有限差分算法，由于需要對人工截斷邊界進行處理并考慮瑞雷波的影響深度(實際模型大小為80 m×60 m)，此算例中的計算耗時為390 s，若將網格剖分為0.05 m×0.05 m并同時滿足相同采樣間隔的要求，則計算耗時上升至3192 s.而對于圖2a所示的層狀模型，基于聚束分析的多道瑞雷波頻散曲線正演算法無需對模型進行深度方向上的網格細分，在此算例中計算耗時僅為0.5 s，若將網格單元的寬度設置為0.05 m，計算耗時也僅為0.7 s，能夠滿足多組模型以及模型中參數變化影響的快速計算分析.

3.2 含低速異常模型

如圖4a所示，在該模型20～40 m范圍內存在一橢圓形低速異常體，該橢圓的長軸和短軸分別為10 m和1 m，模型中泊松比為常數0.333、密度均勻為1900 kg·m-3，地層中橫波速度由上到下依次為120 m·s-1、170 m·s-1和270 m·s-1，低速異常體的橫波速度為100 m·s-1.圖4b為利用全波場模擬得到的共炮點道集，由于此模型在橫向上的不均勻性相較于上個模型要更弱，因此在單炮記錄中瑞雷波視速度的變化也更緩一些.

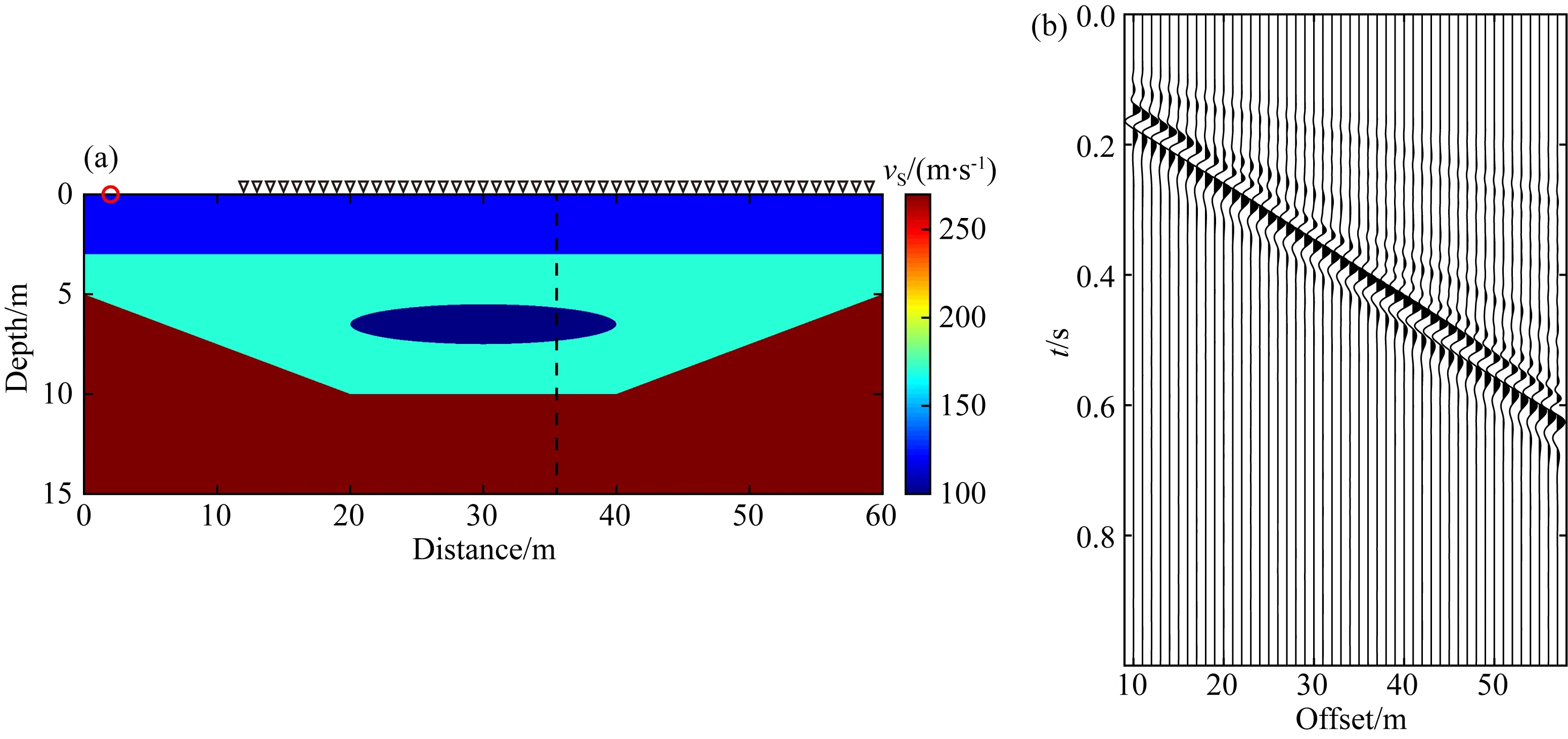
圖4 含低速異常模型及相應的單炮記錄(a) 含低速異常模型，紅色○和黑色分別表示激發震源和接收點的位置，黑色虛線代表接收排列中點； (b) 模擬的共炮點道集.Fig.4 Low-velocity anomaly model and the corresponding single-shot record(a) Low-velocity anomaly model. The red ○ and black represent the positions of source and receivers, respectively; (b) The simulated common-shot gather.

圖5a為利用式(9)計算得到的理論輸出功率譜以及利用黃金分割極值搜索得到的理論多道瑞雷波頻散曲線(白色點線), 圖中黑色虛線代表波數k=2π/L.在模型離散過程中，每個網格單元的寬度固定為0.1 m、厚度根據模型設定.圖5b為利用式(5)對模擬單炮記錄進行波場變換得到的頻散圖像，圖中黑色虛線代表波數k=2π/L.同樣地，這里只對5～50 Hz頻段范圍內的分量進行分析，從頻散圖像中提取的頻散曲線如圖5b中的黑色點線所示.基于振幅歸一化聚束分析的多道瑞雷波頻散曲線正演算法計算得到的理論相速度值如圖5b中的白色點劃線所示，在整個頻段范圍內理論頻散曲線與提取的頻散曲線一致性較高，并且在此模型中頻散圖像受近場效應的影響要更弱，差異主要集中在8.5～10 Hz頻段范圍內，這是由于低速異常體引起的散射瑞雷波導致的，理論頻散曲線與提取頻散曲線之間的均方根誤差為1.51 m·s-1.接收排列中點處的局部頻散曲線如圖5b中的黑色點劃線所示，由于模型淺層的橫波速度無任何橫向變化，局部頻散曲線與提取頻散曲線的差異主要集中在低于18 Hz的頻段范圍內，此范圍內相速度值要低于從頻散圖像中提取得到的相速度值，兩者之間的均方根誤差為7.12 m·s-1.接收排列下方所有局部頻散曲線的平均值如圖5b中的藍色點劃線所示，平均頻散曲線與提取頻散曲線的差異也主要是在頻率低于18 Hz的范圍內，兩者之間的均方根誤差為3.03 m·s-1.

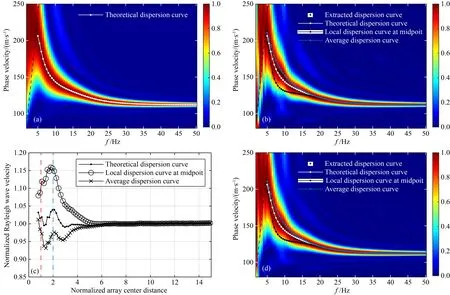
圖5 含低速異常模型頻散分析結果(a) 基于振幅歸一化聚束分析得到的理論功率譜，白色點線為極值搜索得到的理論多道瑞雷波頻散曲線，黑色虛線代表波數k=2π/L； (b) 模擬的單炮記錄進行波場變換得到的頻散圖像，黑色點線為提取得到的頻散曲線，白色點劃線為正演得到的理論頻散曲線，黑色點劃線為排列中點處的局部頻散曲線，藍色點劃線為排列下方的平均頻散曲線，黑色虛線代表波數k=2π/L； (c) NACD-NRWV曲線圖，黑色點劃線、○標注線和×標注線分別為以理論相速度、局部相速度、以及平均相速度作為參考速度計算得到； (d) 利用最小偏移距為1 m、5 m和10 m的單炮記錄得到的疊加頻散圖像，圖中線條表征與(b)一致.Fig.5 Results of dispersion analysis for low-velocity anomaly model(a) Theoretical output power of the amplitude-normalized beamforming. The white dotted line represents the multichannel Rayleigh wave dispersion curve obtained by the local maximum search. The black dashed line indicates wavenumber k=2π/L; (b) Dispersion image generated from the simulated common-shot gather. The black dotted line indicates the extracted dispersion curve, the white dot-solid line represents the theoretical dispersion curve, the black dot-solid line is the local dispersion curve at the midpoint of receiver array, and the blue dot-solid line represents the average phase velocity beneath the entire receiver array. The black dashed line indicates wavenumber k=2π/L; (c) The plot of normalized Rayleigh wave velocity versus normalized array center distance. The black dot-solid line, the ○ marked line, and the × marked line are calculated by the theoretical phase velocity, local phase velocity, and average phase velocity. (d) Stacked dispersion image generated by common-shot gathers with the nearest offset of 1 m, 5 m and 10 m. The representation of plotted lines is the same as (b).

圖5c為將理論頻散曲線、局部頻散曲線和平均頻散曲線作為參考相速度值計算得到的NACD-NRWV曲線圖.利用理論頻散曲線作為參考值得到的曲線如圖5c中的黑色點劃線所示，在歸一化排列中心距大于1和大于2的范圍內最大相對誤差都為4%，該誤差對應的相速度點位于受散射瑞雷波影響的頻段內.利用排列中心點處局部頻散曲線作為參考值得到的曲線如圖5c中的圓號標注線所示，在歸一化排列中心距大于1的范圍內最大相對誤差為15.9%，在大于2的范圍內最大相對誤差為14.8%，可知在此情況下排列中點假設仍然是不成立的.利用排列下方局部頻散曲線的平均值作為參考相速度值得到的曲線如圖5c中的叉號標注線所示，在歸一化排列中心距大于1的范圍內最大相對誤差為6.9%，在大于2的范圍內最大相對誤差為4.6%.

地下存在橫向不均勻性產生的散射瑞雷波將嚴重影響頻散圖像的質量(Yilmaz and Kocaoglu，2012；Mi et al.，2017)，而通過疊加不同偏移距數據的頻散圖像可以較好地壓制非一致性噪聲(Neducza，2007；Socco et al.，2009；Pasquet and Bodet，2017).對于相同模型，保持接收排列固定不變，將最小偏移距分別設置為1 m和5 m并進行全波場模擬，然后將1 m、5 m和10 m三種偏移距單炮記錄得到的頻散圖像進行疊加，疊加結果如圖5d所示，圖中黑色點線為從疊加頻散圖像上提取的頻散曲線，稱之為疊加頻散曲線.由圖可見，疊加頻散圖像受散射瑞雷波的影響較弱，基于振幅歸一化聚束分析的多道瑞雷波頻散曲線正演算法計算的理論相速度值與提取得到的相速度值之間的一致性有所提升，兩者之間的均方根誤差為0.95 m·s-1，理論頻散曲線與疊加頻散曲線之間的平均相對誤差為0.4%，最大相對誤差為2.5%.在頻率低于18 Hz范圍內，排列中點局部頻散曲線的相速度值仍低于提取得到的相速度值，兩者之間的均方根誤差為6.60 m·s-1，局部頻散曲線與疊加頻散曲線之間的平均相對誤差為2.0%，最大相對誤差為12.2%.平均相速度值與提取得到的相速度值之間的均方根誤差有所上升，為3.38 m·s-1，兩者之間的平均相對誤差為1.1%，最大相對誤差為7.6%.可以看出，基于振幅歸一化聚束分析的多道瑞雷波頻散曲線正演算法計算得到的相速度值與波場模擬分析得到的相速度值之間的誤差較小，具有較高的可靠性.

4 結論

本文基于振幅歸一化聚束分析，提出了一種適用于橫向不均勻介質模型情況下的多道瑞雷波頻散曲線快速正演算法，并通過與二維彈性波時間域有限差分模擬結果對比驗證了該算法的可靠性.理論模型分析揭示，對于橫向不均勻地下介質，利用面波多道分析法提取得到的頻散曲線是接收排列下方介質的綜合反映，但不是接收排列下方局部頻散曲線的簡單算術平均，更不能認為是接收排列中點處的介質響應.本文算法研究可為面波多道分析法的觀測系統優化提供技術支撐，并且將該方法引入頻散曲線的反演解釋有望克服當前面波多道分析法在橫向不均勻介質探測中水平分辨率的限制，提升反演結果的可靠性.從理論上講，該算法也適用于其他類型導波(如勒夫波、Scholte波等)在橫向不均勻介質中的多道頻散曲線計算，而如何考慮多模式面波的傳播，以及相應的多道頻散曲線正演算法，將是更具理論意義及實際應用價值的新探索.