逆濾波器設計中若干基本問題的探討*

曲萬春，何國榮，梅鐵民

（沈陽理工大學，遼寧 沈陽 110159）

0 引言

在很多信號處理應用中，如信道均衡、語音去混響[1-2]、能譜檢測[3]、軌道不平順檢測信號處理等[4]，都需要求解已知線性系統的逆系統，即逆濾波器設計。逆濾波器設計方法有很多，如最小均方誤差[5-7]、復倒譜法[8]、基于LMS或卡爾曼濾波的算法等[9]，其中最簡單也最常用的方法是最小均方誤差設計方法。最小均方誤差法設計的逆系統與原系統的級聯在均方誤差最小化意義下逼近一個純時延全通系統。

在最小均方誤差逆濾波器設計中，一個經常被忽視的問題是原、逆濾波器級聯系統所逼近的全通系統的時延問題（或群延遲問題）[6]。級聯系統的時延大小取決于原系統的相位特性。最小均方誤差逆濾波器設計包括單輸入-單輸出系統（Single Input Single Output，SISO）、單輸入-多輸出（Single Input Multiple Output，SIMO）系統和多輸入-多輸出（Multiple Input Multiple Output，MIMO）系統的逆系統設計。本文中只討論前兩種情況。

1 SISO系統的逆系統設計

設單信道系統的輸入輸出關系為：

式中，s(n)和x(n)分別為系統的輸入、輸出信號；c(n)(n=0,1,2,…,Lc-1)為系統的單位取樣響應。

式（1）的z域表示為：

在最小均方誤差意義下使g逼近理想系統ql：

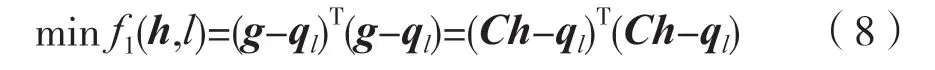
式中，ql=[0,0,…,1(第l個分量),0,…,0]T是Lg×1維列矢量，代表一個純時延的理想全局響應。

式（8）的最小均方解為：

式中，列矢Cl=CTql是卷積矩陣C的第l行的轉置。

最小均方誤差值為：

如上所述，SISO系統只能得到最小均方誤差意義下的最優逆濾波器，不可能得到完全解卷積的逆濾波器，但SIMO系統可以得到完全解卷積逆系統。

2 SIMO逆系統設計

SIMO系統與SISO系統相比，具有本質上的不同，有完全解卷積的有限沖激響應逆系統。SIMO系統的輸入輸出關系為：

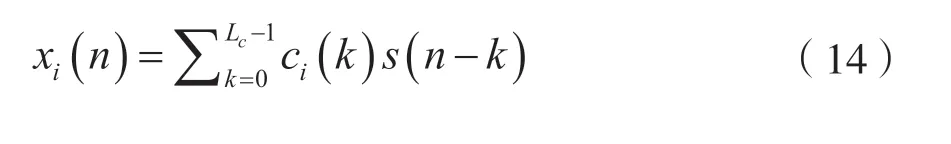
式中，i=1,2,…,N，xi(n)和ci(n)分別是第i路信道的輸出信號（觀測信號）和單位取樣響應；s(n)是系統的輸入信號。在N路信道沖激響應ci(k)已知且各個信道間沒有公共零點的情況下，多路解卷積系統由MINT定理給出[5-6]。

令N路解卷積濾波器為hi(n)(i=1,2,…,N;n=0,1,…,Lh)，則解卷積信號為：

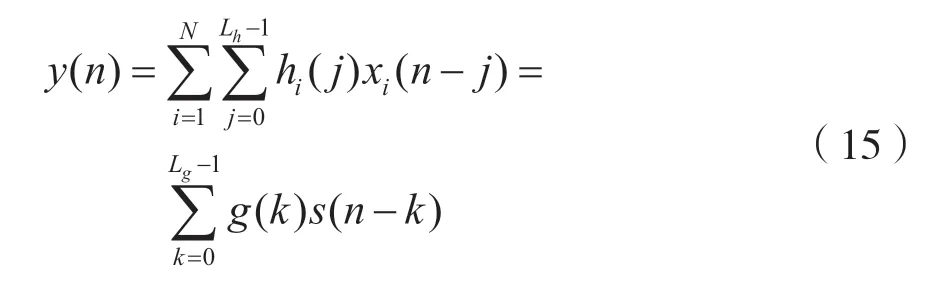
式中，全局響應g(k)可表示為：

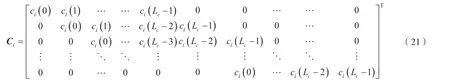
則SIMO解卷積問題等價于如下的優化問題：

當Lc、N不同值時，由得到的Lh值不一定是整數。如果Lh取大于的整數，則LgNLh，式（23）為超定問題，有唯一最小二乘解：

方法描述如下：設N路解卷積濾波器的長度分別為Lh1,Lh2,…,LhN，不失一般性地假設Lh1最大，且則全局響應的長度Lg=Lh1+Lc-1。分配各個解卷積濾波器的長度值，使得解卷積濾波器組構成的矢量總長度滿足條件：

考慮到Lg=Lh1+Lc-1，式（26）也等價于：

式（28）同時隱含了對每一個解卷積濾波器長度的約束條件：

當Lh1,Lh2,…,LhN給定后，即可構造矩陣其中Ci矩陣仍如式（22）定義，但只取其前Lhi列，這樣得到的濾波器組可以實現完全解卷積。由于Lh1,Lh2,…,LhN的取值有不同的組合，再加上不同的取值，因此完全解卷積濾波器組并不唯一。此外，如果假設Lh2=Lc-1，則Lhi=0(i≠1,2)，即只有兩路觀測信號即可實現完全解卷積，也說明多路信號解卷積中至少要有兩路觀測信號才能實現完全解卷積。

3 仿真實驗

3.1 SISO系統仿真實驗

在這個仿真實驗中，原系統沖激響應c0(n)是仿真得到的Lc=800的房間沖激響應序列，如圖1所示。

圖1 原系統的沖激響應序列c0(n)

為了模擬原系統沖激響應c0(n)估計誤差對全局響應g(n)的影響，在原系統沖激響應上增加不同強度的零均值高斯白噪聲，即c(n)=c0(n)+v(n)，用估計誤差信噪比來表示c(n)估計精度。在最佳全局響應時延下得到最小均方誤差意義下的解卷積濾波器h(n)后，計算全局響應g(n)=c0(n)*h(n)相對理想全局響應q(n)的均方誤差為：

圖2中給出了ERR(SIR,Lh)與SIR、Lh之間的關系曲線。可以看出，對于給定的原系統估計誤差信噪比SIR，解卷積濾波器越長（圖2中的曲線由下向上對應Lh由100增加到1 500），解卷積效果越好，但隨著解卷積濾波器長度的增加，解卷積效果的改善越來越小；對于給定長度Lh解卷積濾波器，原系統估計誤差的SIR達到某個值（隨Lh增大而增大）以上時，對解卷積結果影響很小，這時卷積結果的誤差主要取決于解卷積系統h(n)的逼近誤差。因此，對于給定長度的解卷積濾波器，一味增加原系統估計精度是沒有意義的。

3.2 SIMO系統仿真實驗

4路實測房間沖激響應用于SIMO系統解卷積仿真實驗Lc=818，如圖3所示。

在滿足MINT的定理條件下，首先定義不同原系統估計誤差信噪比SIR、不同全局響應時延l對應的全局響應均方誤差函數ERRMINT：

4個解卷積濾波器的長度分別為Lh1=Lh2=273，Lh3=Lh4=272。原系統c0(n)估計誤差信噪比SIR對全局響應均方誤差ERR的影響如圖4所示。圖4中每條曲線對應不同的全局響應時延l=0,20,40,…,1 080。從圖4可見，只有在高估計誤差信噪比下，ERR近似地隨SIR的增加而線性增加；當SIR較低時ERR很小，甚至為負值，無法實現解卷積。

圖2 原系統c0(n)估計誤差SIR（橫軸）、解卷積濾波器長度Lh（對應圖中不同曲線）對全局響應均方誤差（縱軸）的影響（曲線的排列順序與圖例的順序一致）

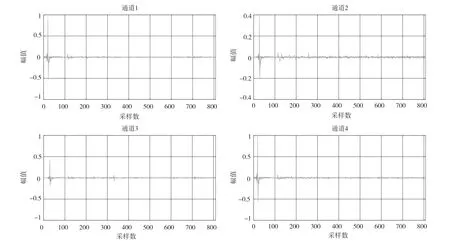
圖3 房間4通道沖激響應序列

對ERRMINT(SIR,l)在SIR方向取平均，得到，如圖5所示。找到圖5中最大值對應的l值，即為最優全局響應時延，在本例中l=100。

對于SIMO系統，在不滿足MINT定理時得到的是在最佳全局響應時延下的最小均方誤差解。解卷積濾波器等長并滿足關系（向下取整，在本例中Lh≤272），仍用式（30）中的ERR來衡量算法性能，結果如圖6所示。與SISO系統的結果類似，即越逼近其上限，解卷積效果越好，但噪聲穩定性越差。圖6中每條曲線對應不同解卷積濾波器長度Lh=27、54、81、108、135、162、189、216、243、270。

圖4 在滿足MINT定理條件下，全局響應均方誤差ERR與原系統c0(n)估計誤差信噪比SIR關系曲線（每條曲線對應不同的全局響應時延0,20,40,…,1 080；粗黑線對應最佳全局響應時延下的ERR）

圖5 不同SIR下的平均ERR曲線（曲線最大值位置對應最優全局響應時延l=100）

圖6 在不滿足MINT定理條件下，全局響應均方誤差與原系統估計誤差信噪比SIR關系曲線

4 結語

理論上，SISO系統的逆濾波器長度越長越好，但由于有限沖激響應逆系統只是理想逆系統的最小均方誤差逼近，因此在原系統存在估計誤差時，過長的逆濾波器并不能提高解卷積性能，反而增加計算負擔。對于SIMO系統，正如文獻所述，滿足MINT定理的逆系統對噪聲過于敏感，而不滿足MINT定理的最小均方誤差逆系統相對來說噪聲穩定性更好，且該最小均方誤差逆系統的沖激響應的長度是有上限的。它的上限由MINT定理給出，這與SISO系統截然不同。此外，無論是SISO系統還是SIMO系統，都可以通過對全局響應時延優化來改善逆系統性能。