Ku頻段衛星通信信號自適應檢測算法*
李 成,白 園,陳 飛
(中國電子科技集團公司第三十研究所,四川 成都 610041)
0 引言
近年來,衛星通信以其頻譜資源豐富、支持寬帶信號傳輸、覆蓋廣、受地理條件限制小等優點,逐漸在軍民領域都占有不可替代的重要地位。隨之而來的是衛星通信的需求不斷增加,支持的應用不斷擴展,不明體制、私有協議的信號增多,新的調制方式出現,在非合作條件下,對寬頻段衛星信號的截獲與分析帶來了極大的挑戰。
目前,國內針對衛星信號的檢測方法如小波變換法[1]、能量檢測法[2]、希爾伯特變換法等能夠在給定某些先驗知識的前提下實現對衛星信號的檢測,然而需要一定的人工介入,不能滿足對衛星信號檢測自適應和普適性的要求。
本文針對以上問題展開研究,首先對Ku頻段衛星電磁頻譜特征進行分析,采用改進的周期圖法與頻域低通濾波的方法對信號頻譜進行改善,使其更有利于信號檢測。其次,在完成全頻段頻譜擬合拼接的基礎上設計了一種合理的迭代策略,能夠完成背景噪聲統計與檢測門限設定,最終根據信號能量與帶寬完成目標信號的檢測。
1 Ku頻段通信衛星電測頻譜分析
工作中發現某典型同步軌道通信衛星Ku頻段轉發器電磁頻譜如圖1所示。可以看出,該衛星信號個數較多、帶寬范圍跨度較大,且集中在同一頻段。同時,在非合作接收條件受限情況下,發現某些信號包絡的起伏較大,背景噪聲變化較大,極易造成信號檢測虛警或漏判。故需要采用一定的方法對頻譜進行處理,此為提高信號檢測成功率的基礎。

圖1 某衛星信號頻譜
2 頻譜預處理
2.1 頻譜平滑
信號頻譜處理首先要進行頻譜平滑,比較常見的是周期圖譜估計法[3]。它取隨機信號x(n)的N點觀察數據xN(n)直接進行FFT,得到頻譜的估計值xN(ω),平方后再除以N,就得到功率譜的估計值,即p(ω)=|xN(ω)|2/N。考慮到在周期圖法中對xN(ω)求平方會大大增加硬件計算時間,故本文對上述周期圖法進行改進。該方法的思想是對連續接收信號進行分段處理,即根據實際處理帶寬和采樣率選取合適的FFT點數,然后在時域上截取相同點數的數據做FFT,進一步得到該段信號的周期圖,然后對每段數據處理結果求平均,即得到處理帶寬范圍內初步平滑的頻譜。式(1)~(4)給出該方法的一系列公式。
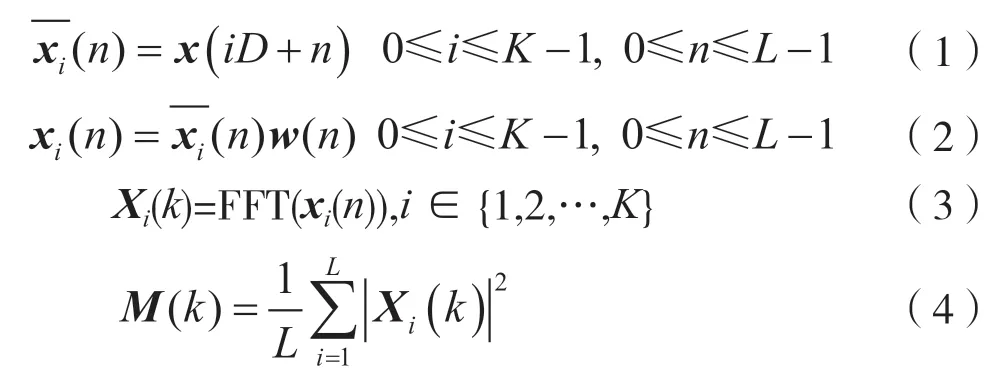
式中,K為連續數據的分段數,每段的FFT點數為L,D指各段數據之間的相對偏移量。
采用本文提出的改進方法,得到功率平均后的頻譜,能夠大大減小頻譜估計的方差。但是當檢測時間受限時,一味地增加分段數和數據長度,將不能滿足實時處理的需求。因此,要綜合考慮處理帶寬、采樣頻率、硬件計算時長等參數,選擇合適的數據分段數和每段的數據長度。本文工程中選擇將一次處理數據分為20段,每段數據長度為16 384。
圖2和圖3分別為對某Ku頻段衛星實采信號直接進行FFT變換得到的頻譜圖和采用改進算法得到的頻譜圖。可以看出,圖3信號的頻譜明顯得到了改善,毛刺也明顯減少。
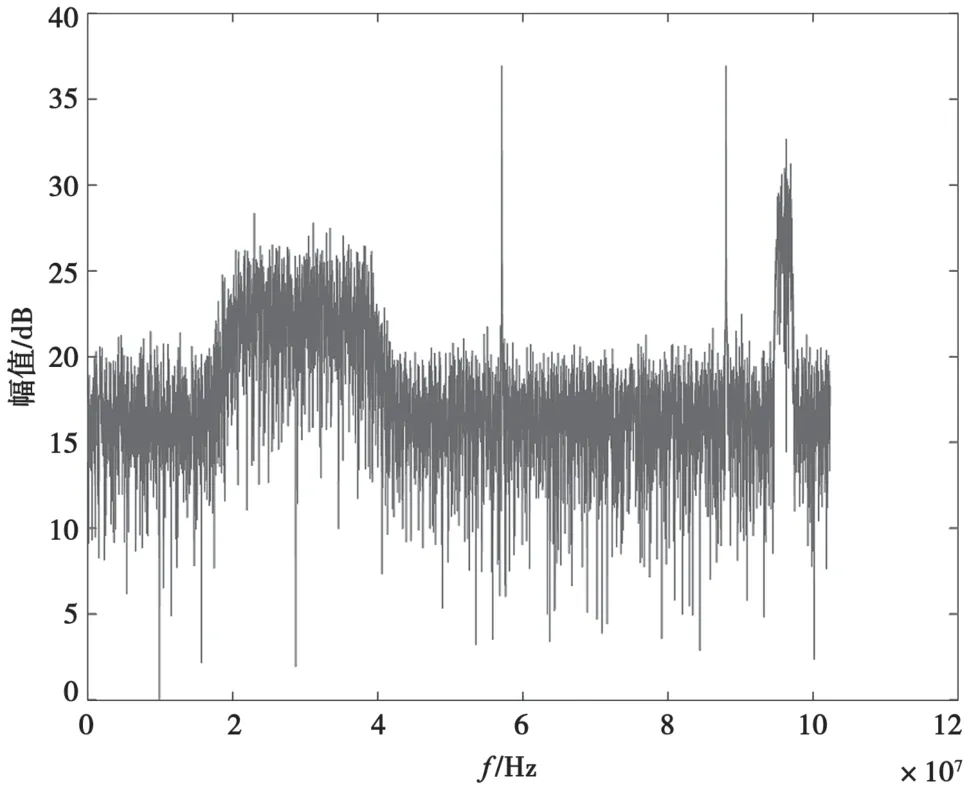
圖2 周期圖法信號頻譜
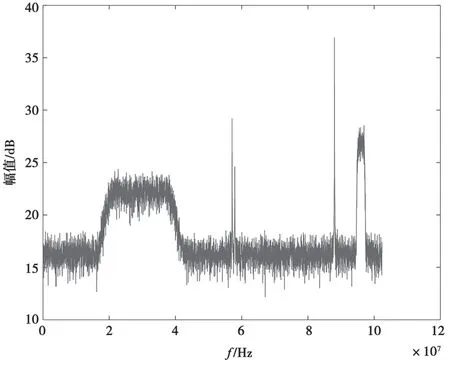
圖3 改進的周期圖法信號頻譜
采用本文方法可使處理帶寬范圍內信號的頻譜變得比較平滑,但是其平滑程度仍然不足以用來做信號的自動檢測。借鑒數字圖像處理中圖像平滑的方法,本文對初步平滑處理后的頻譜進行低通濾波,來進一步降低譜估計方差、減少毛刺。
較高階數的頻域低通濾波器能夠使信號頻譜得到顯著的平滑效果,然而過度的平滑意味著“模糊不清”。所以在設計低通濾波器的時候,不能無限制地增加濾波器的階數,當平滑濾波后的頻譜能夠比較準確地完成信號自動檢測時就夠了。另外,由于濾波器的延遲效應,平滑后的頻譜會出現“頻率右移”的現象,所以應該根據實際情況來確定合理的濾波器參數。本文選用漢寧窗函數,階數為30階,采樣率為102.4 MHz,通帶截止頻率為10 kHz,對圖3中的頻譜進行頻域平滑濾波,結果如圖4所示。可以看到,平滑濾波器對于連續譜如恒包絡的寬帶信號有一定的提升效果,對于離散譜如FSK、單音等信號則有一定的降低效果。這種效果對于后續的信號自適應檢測非常有利。
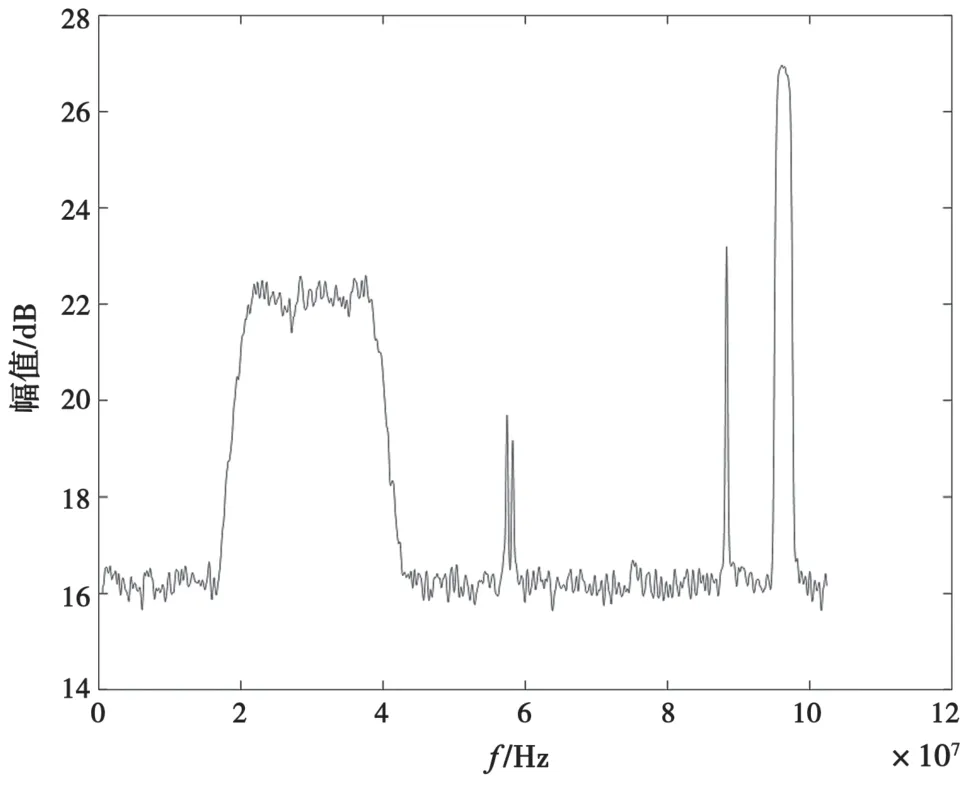
圖4 頻域平滑濾波后的頻譜
2.2 基于最小二乘擬合的頻譜拼接
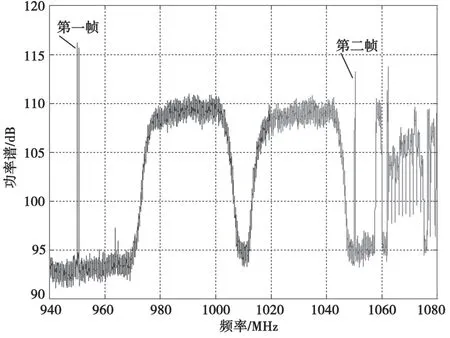
實際應用中通常需要對整個Ku頻段(10.95~12.75 GHz)頻譜進行計算,以便更準確地估計背景噪聲。由于接收設備的帶寬限制,每次只能計算一個瞬時帶寬內的頻譜(稱為一幀頻譜),故需要多次改變接收頻點進行頻譜拼接,獲得整個頻段內的完整頻譜。然而每次計算時間存在先后,由于噪底、信號功率等可能的抖動,以及硬件設備(變頻、濾波、采集)本身的一致性問題,會導致相鄰兩次計算出的頻譜存在差異,使得拼接后的頻譜在前后頻點交界位置出現真實中并不存在的能量階躍或者比例變化,如圖5所示。
故可采用如下處理,掃描時讓前后幀頻譜存在部分重疊,利用重疊部分頻譜對后一幀頻譜的基準電平、尺度進行估計,補償后再進行拼接[4]。
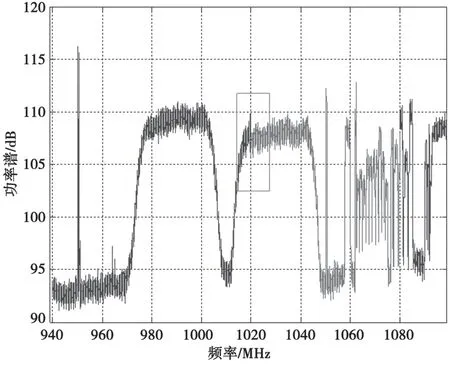
圖5 原始幀頻譜拼接
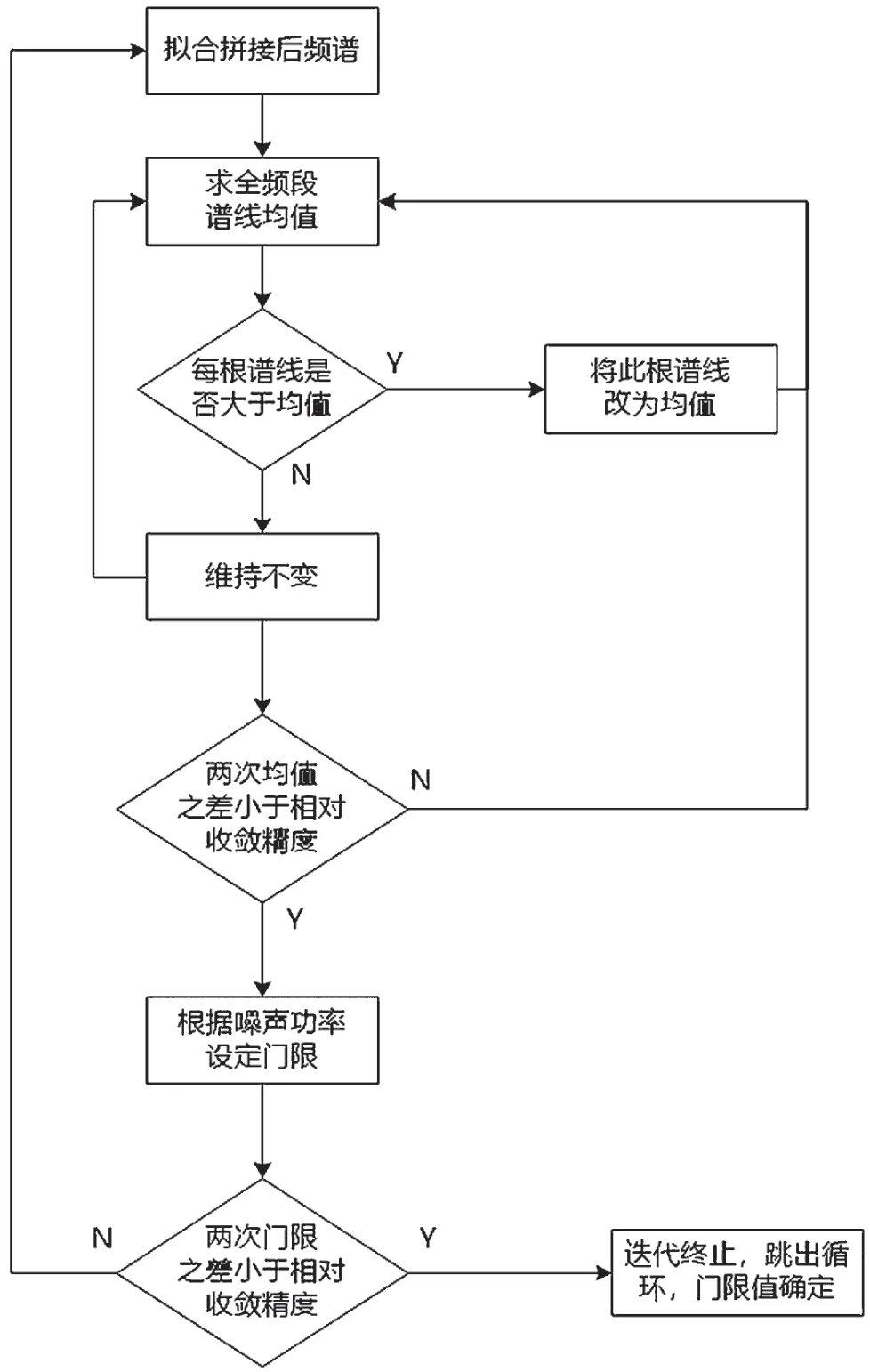
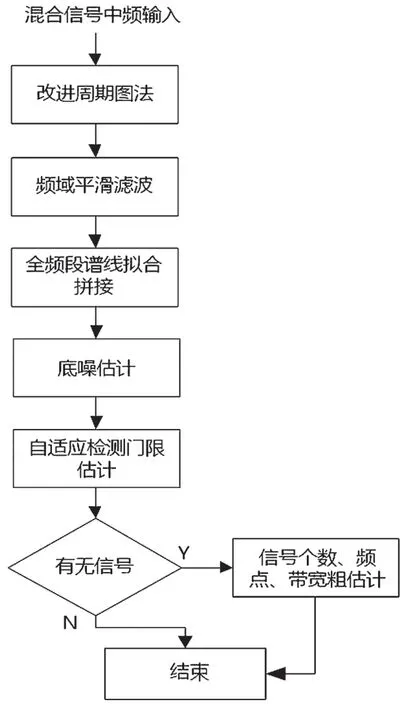
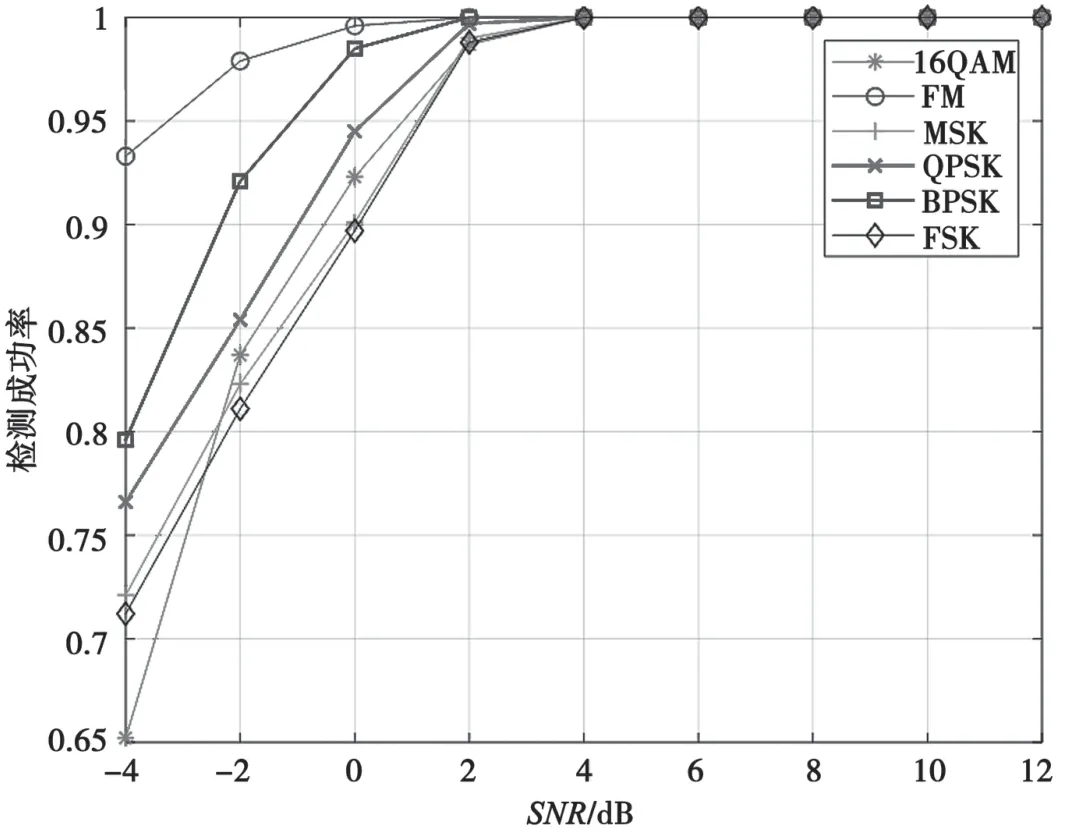
設x1(f),f∈[f1,f3]為第一幀對數頻譜,x2(f),f∈[f2,f4]為第二幀對數頻譜,其中f1 對式(5)的離散形式,可采用最小二乘方法估計出a、b后,計算補償后的頻譜ax2(f)+b,然后進行拼接。 對圖5中的頻譜進行擬合拼接,結果如圖6所示。 圖6 擬合拼接后的頻譜 經過改進的周期圖法和頻域低通濾波處理后的信號頻譜底噪起伏非常小,再經擬合拼接,即可在全頻段頻譜中比較準確地統計背景噪聲,并在此基礎上設計合適的自適應檢測門限。 目前,比較常用的能量檢測門限設計準則有以下兩種:恒虛警概率準則[5],指要求在保持恒定的虛警概率的條件下,使信號正確檢測的概率達到最大值Pf;恒檢測率門限準則[6],指能量檢測的判決期望對信號檢測概率小于或等于一個性能指標Pd。 在實際應用中,由于不同用戶發射的信號功率可能不同,不同轉發器輻射的EIRP值也可能不同,導致接收不同頻段的信號能量不同,恒漏檢率和恒虛警率均對判決結果有很大的影響,且根據實際場景的不同,對判決結果的影響也不同。因此,基于以上兩種門限設計準則都不太適合本文自適應檢測的需求。綜合考慮,在先驗信息全盲的條件下,為使虛警率和漏檢率都盡可能小,對二者加權求和后求最小值,以此作為最優門限設計準則。 采用最優門限準則能達到的錯判率門限[7]最小值為: 根據上述最優門限設計準則,本文提出如圖7所示的自適應門限迭代策略。 具體流程如下:第1步,求出經平滑處理和擬合拼接后的全頻段頻譜幅值的平均值,記作Nth1。第2步,基于頻譜分辨率,將每個頻點對應的譜線幅值與該平均值做比較,幅值小于或等于Nth1的值不變,大于Nth1的將其值改為Nth1。第3步,求出新得到的這一組全頻段譜線的平均值Nth2,然后進行和第2步同樣的操作,直到前后兩次的平均值之差小于一個相對收斂精度(本文采用經驗值)為止,可得到比較準確的底噪估計值,將其記為Nth2。在硬件實現時,為了簡化算法的復雜度,直接將底噪估計迭代次數最大值定為3次。第4步,根據底噪估值和式(6)計算初始判決門限Vth1。第5步,取第二次全頻段譜線重復上述過程,計算新的判決門限Vth2,同樣的,直到前后兩次的門限值之差小于一個相對收斂精度(同樣采用經驗值)為止,迭代運算就會收斂,運算終止,得到最終的自適應檢測門限。 圖7 自適應門限迭代策略 將全頻段信號譜線幅值和自適應判決門限Vth做比較,將譜線幅值大于判決門限的點的坐標保存到數組R中。除了特殊體制如PCMA外,衛星信號通常不會在頻域混疊。利用每兩個信號之間默認存在頻率間隔這一點,進行R[i+1]-R[i]計算,如果R[i+1]-R[i]=1,說明這兩個譜線幅值是一個信號中頻率相鄰的兩個點。如果R[i+1]-R[i]>1,那么這兩個譜線幅值有可能是兩個信號起始頻率和截止頻率分別對應的坐標,但也有可能是較大的噪聲毛刺或信號過渡帶頻譜形狀出現凹陷的兩個頻點對應的坐標。另外,頻率間隔設置過大則有可能將兩個信號誤判為一個信號,故需根據實際頻率分辨率來設置頻率間隔。本文中設置R[i+1]-R[i]>50,能夠使多個信號的檢測成功率得到極大提升。 基于上述自適應門限迭代策略,在實際衛星信號檢測場景中能夠準確檢測出多個信號。同時,頻率分辨率是已知的,那么可以得到每個信號的起始頻率f1和截止頻率f2的準確粗估計值。所以信號的中心頻率粗估計值fc=(f1+f2)/2,信號的帶寬粗估計值B=f2-f1。圖8給出自適應檢測的流程圖。 設置采樣率為102.4 MHz,檢測頻段10.95~12.75 GHz,包含FM、BPSK、QPSK、16QAM、MSK、FSK等6種混合仿真信號。運用本文算法在每個信噪比下進行1 000次蒙特卡洛檢測仿真,其檢測成功率與信噪比關系如圖9所示。 通過仿真發現,本文算法在信噪比大于2 dB時,混合信號的自適應檢測成功率幾乎可以達到100%,具有較好的性能;迭代次數少且沒有大量乘法運算,硬件計算時間較少,易于工程實現;適用于各種調制方式的衛星信號,通用性較好。 圖8 自適應檢測流程 圖9 仿真信號正確檢測率與信噪比的關系 本文提出了一種針對Ku頻段衛星通信信號的自適應檢測方法,能夠準確估計全頻段底噪,自動設置合適的檢測門限,在此基礎上得到的信號個數、頻點、帶寬的粗估計值正確率高。本文算法在設計同時就已經考慮了工程實現的可行性問題,目前該方法已應用于實際工程項目。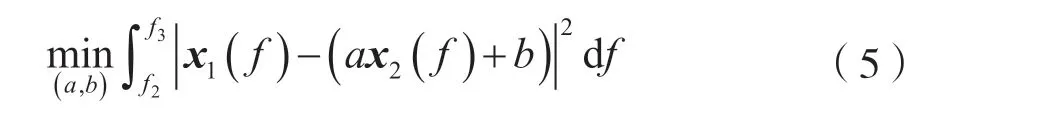
3 自適應檢測算法
3.1 底噪估計及門限設置

3.2 多信號自適應檢測與粗估計
4 仿真試驗及性能分析
5 結語

