改進孿生神經網絡的控制圖模式識別方法
劉青星,黃海松,姚立國,胡 耀,3
1(貴州大學 機械工程學院,貴陽 550025)
2(貴州大學 現代制造技術教育部重點實驗室,貴陽 550025)
3(貴州人和致遠數據服務有限責任公司,貴州 550025)
1 引 言
控制圖是基于統計學原理,對生產過程中關鍵工序參數或產品質量特征觀測值[1]進行統計分析,判斷制造系統是否處于穩定可控狀態.當制造過程出現不穩定因素時,控制圖便會產生異常波動,反映出制造系統中的異常因素.生產者根據控制圖波動模式采取相應措施,消除生產過程中的異常因素,控制產品質量的穩定性.過去對控制圖的識別依賴生產者的經驗,難以實現對控制圖模式的實時識別,有礙于智能制造產業的發展.隨著機器學習和深度學習算法的興起,對控制圖異常模式識別不再依賴于傳統的控制界限或人的經驗,而是運用機器學習、深度學習等智能算法識別控制圖的異常模式.
在機器學習領域,識別控制圖異常模式的步驟為:特征提取、維數簡約、分類器選擇等.首先提取控制圖包含的質量特征,主要包含統計特征[2]、形狀特征[3]、小波分解特征[4]等.再對質量特征進行融合,如統計特征與形狀特征融合[5]、統計特征與原始數據融合等.質量特征融合后,融合特征的維數較大,常利用PCA、KPCA、KECA[6]、ICA[7]等降維算法進行特征簡約,最后使用支持向量機[8]、極限學習機[9]、隨機森林等分類器對控制圖特征進行識別.使用機器學習方法對控制圖進行特征識別時需要人工提取質量特征,忽略了數據之間的關聯性,容易出現過擬合.
由于深度學習對大數據具有很好的分類效果,且無需人工提取數據特征,能很好的運用特征之間的相關性對控制圖進行模式識別.因此,卷積神經網絡[10]、遷移學習[11]、脈沖神經網絡[12]等深度學習的方法也被運用于控制圖的識別.深度學習雖然大樣本數據集下有很好的識別性能,但是對樣本量較小的情況識別精度低,不適用于小批量多品種生產過程中的控制圖識別.
孿生網絡是度量學習中的一個重要手段,通過度量樣本之間的空間距離,識別出樣本的分類,在數據量較少時,表現出良好的分類性能,常用于目標跟蹤[13]、文本分類[14]、圖片分類[15]等方面.由于統計過程控制(Statistical Process Control,SPC)的應用在很大程度是對生產制造過程的穩定性進行監控,使得異常控制圖樣本較少,異常模式較多,深度學習的方法難以準確識別異常控制圖.針對上述問題,本文提出的基于PCSNN的控制圖異常模式識別模型,通過度量控制圖樣本的空間距離,衡量控制圖樣本間的相識性,從而實現對控制圖的異常模式識別.隨著生產制造過程的持續,影響生產過程穩定性的異常因素增多,控制圖異常模式的樣本量也隨之增多,PCSNN模型的識別率也優于其他深度學習方法;同時,在生產制造過程中,產品品種的改變會引發控制圖特征參數變動,在此情況下,PCSNN模型也能較好的識別出控制圖的異常模式.
2 控制圖的基本模式
控制圖的基本模式由美國西部電氣公司首先提出,共有8種,如圖1所示,分別為正常模式(Normal,NOR)、循環模式(Cyclic,CYC)、上升趨勢(Uptrend,UT)、下降趨勢(Downtrend,DT)、向上階躍(Upward Shift,US)、向下階躍(Downward Shift,DS)、系統模式(Systematic,SYS)、分層模式(Stratification,STR).控制圖的異常模式,有著各自的表現形式,并代表著生產過程的不穩定狀態與各種異常因素.控制圖的基本模式在生產過程中可用公式(1)進行描述:
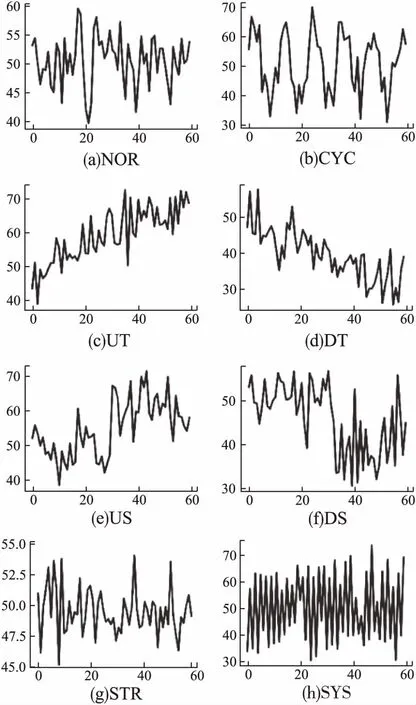
圖1 控制圖基本模式
x(t)=μ+d(t)+r(t)
(1)
式中,x(t)是t時刻控制圖的觀測值;μ是產品質量特征的平均值;d(t)是制造系統中的異常因素所引發的異常模式,當制造系統處于穩定狀態時,則認為d(t)為0;r(t)是制造系統中正常的隨機波動,制造過程處于穩定可控狀態時,r(t)服從正態分布.
3 孿生神經網絡
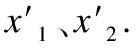
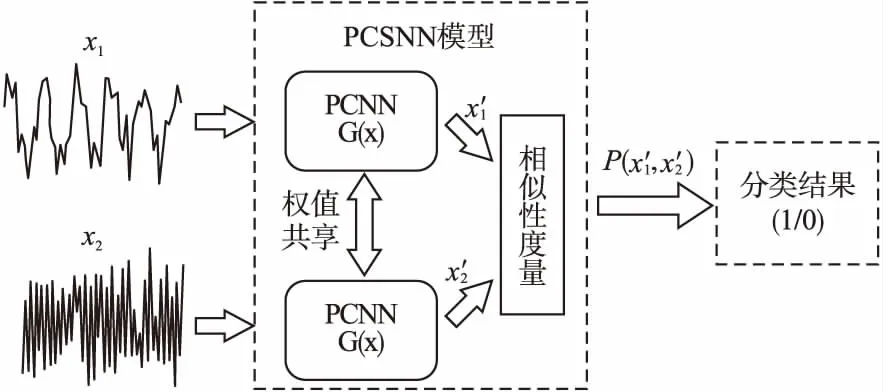
圖2 基于PCNN的孿生網絡
3.1 One-Shot K-Way分類
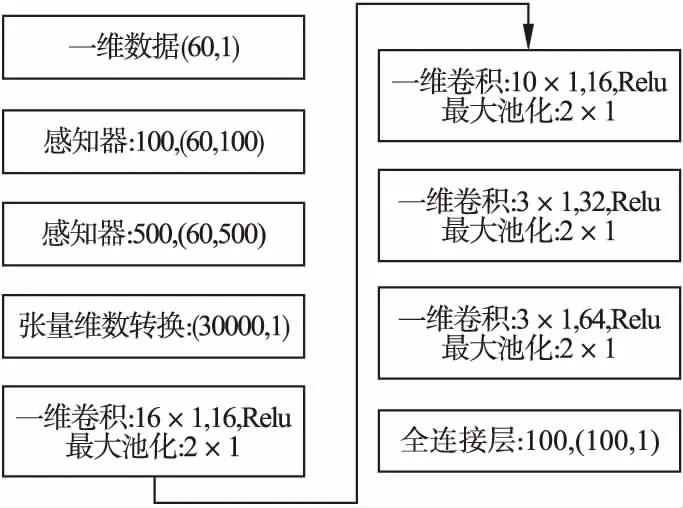
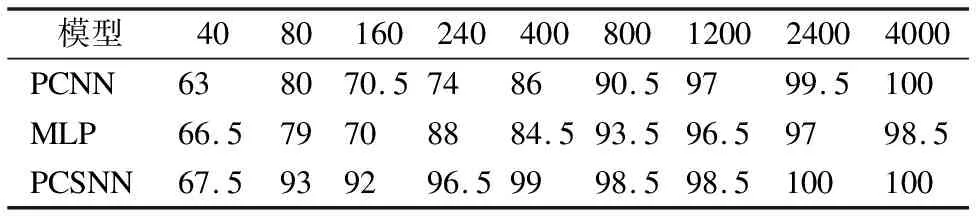
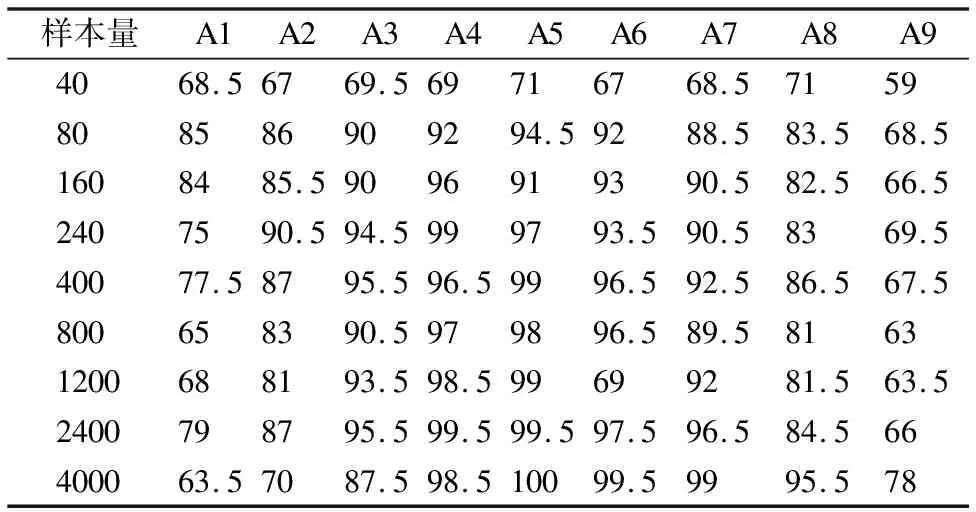
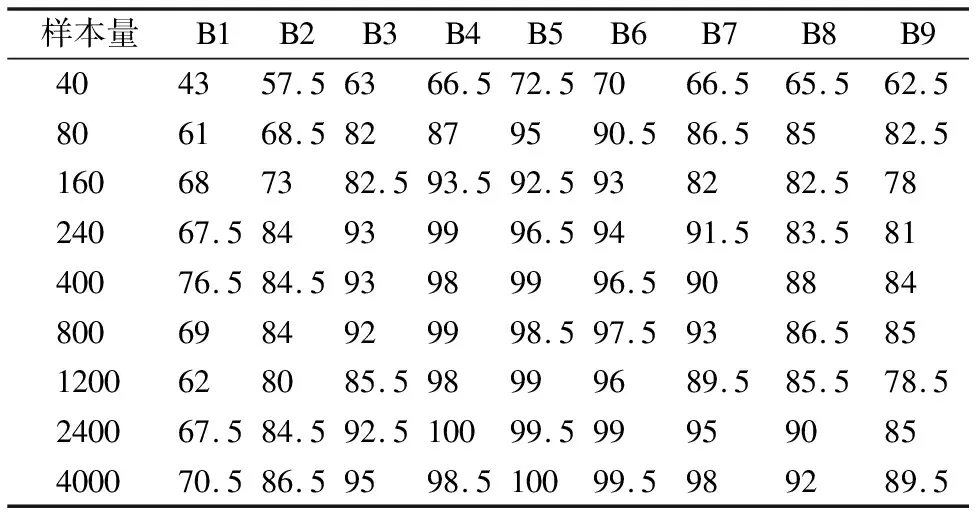
S={(x1,y1),(x2,y2),…,(xk,yk)},k (2) (3) 如圖3所示,多層感知器(Multilayer Perceptron,MLP)是通過非線性激活函數和多層神經網絡實現樣本數據的非線性表達,學習數據特征的非線性關系. 圖3 多層感知器 如圖4所示,卷積神經網絡通過對原始數據進行填充零元素、卷積、池化、展開特征圖等操作.通過將卷積窗口與數據特征進行卷積運算獲取卷積特征,并用激活函數對卷積特征進行非線性映射,獲得原始數據所包含的數據特征. 圖4 一維卷積神經網絡 在實際生產中,控制圖的異常樣本較少,且異常模式較多,同時控制圖樣本的數據點一般較少,卷積神經網絡等深度學習算法難以獲得控制圖所包含的非線性特征,對控制圖的識別率較低.本文基于孿生神經網絡的思想,提出適用于小樣本的控制圖模式識別模型PCSNN,如圖2所示.所設計的孿生網絡的分支網絡PCNN如圖5所示.首先使用兩層感知器將控制圖樣本映射到高維空間,增加控制圖質量特征的維數,解決了因控制圖樣本的質量特征數據點較少導致深度學習方法難以提取特征的問題;使用4層一維卷積神經網絡提取控制圖所包含的非線性質量特征,利用孿生網絡的思想,實現小樣本情況下控制圖的模式識別. 圖5 PCNN模型 用于控制圖樣本維數升維的兩層感知器的激活函數均為Relu函數,第1層感知器包含了100個神經元,先將樣本維數為(60,1)的控制圖映射為(60,100);第2層感知器包含了500個神經元,將質量特征映射為(60,500);為了一維卷積神經網絡能夠提取控制圖的質量特征,對映射后的質量特征張量進行維數轉換,轉換為(30000,1)的張量. 通過卷積網絡獲取控制圖樣本的非線性特征,第1、2個卷積層使用較大的卷積窗口初步提取控制圖特征,卷積窗口尺寸分別為16×1、10×1,卷積窗口數量均為16個.第3、4個卷積層使用較小的卷積窗口尺寸進一步提取微小的特征,卷積窗口尺寸均為3×1,卷積窗口數量分別為32和64.一維卷積神經網絡在每次完成卷積運算后都通過Relu函數對卷積特征進行映射,再進行最大池化處理,池化窗口為2×1.全連接層包含100個神經元,將一維卷積網絡所提取的特征圖通過sigmoid非線性映射函數映射為(100,1)的特征. 3.4.1 質量特征的相似性度量 孿生神經網絡對質量特征進行相似性度量,即:計算兩個樣本相似的概率,一般常用的方法是:①使用公式(4)計算控制圖質量特征向量的空間距離DG(x);②通過公式(5)將控制圖特征向量的空間距離DG(x)映射為樣本相似概率P(x1,x2). DG(x)=‖G(x1)-G(x2)‖ (4) P(x1,x2)=sigm(DG(x)) (5) (6) 式中G(x)為PCNN模型. 3.4.2 PCSNN神經網絡的loss函數與優化函數 PCSNN使用Adam函數作為優化函數.PCSNN的loss函數為正則化的交叉熵函數,如公式(7): (7) 式中y控制圖樣本對是否相識的標簽,相似則為1,不相似則為0;P(x1,x2)為控制圖樣本對(x1,x2)的相似概率. 為了驗證PCSNN模型的有效性,從兩個方面對PCSNN進行實驗驗證:①將PCNN,MLP模型與PCSNN進行對比,對比不同訓練樣本量下PCNN、MLP、PCSNN模型的識別率.PCNN模型如圖5所示,直接使用全連接層提取的特征進行控制圖的異常模式識別,并使用Adam優化器優化PCNN模型;MLP模型使用了5個隱藏層,分別包含200,200,200,200,100個神經元,隱藏層的激活函數均為ReLU函數,且使用Adam優化器對模型進行優化.②對比了PSCNN模型在質量特征參數變動時的識別率.分析在不同訓練樣本量下,質量特征均值與質量特征方差兩個參數變化時,對PCSNN識別率的影響. 為滿足對比實驗的需求,利用Monte-Carlo方法按表1的控制圖參數對8種控制圖模式進行仿真.共仿真9個訓練樣本集,分別包含40,80,160,240,400,800,1200,2400,4000個控制圖樣本,每個樣本包含60個數據點,每個樣本集有8種分類,如表2所示,控制圖均值μ=50,標準差σ=5. 表1 控制圖參數 根據表2,使用表1的控制圖參數,仿真2組測試集A、B,每組9個測試集,每個測試集中包含8種控制圖基本模式,每種模式有25個測試樣本,共計200個測試樣本.由于A5、B5仿真時均值為50,方差為5,故而A5、B5測試集為同一個,同時也是MLP、PCNN、PCSNN對比試驗的測試集. 表2 測試集的均值與方差 本節將A5作為測試集,分別測試在9個不同訓練樣本量下,PCSNN、MLP、PCNN的識別精度,測試結果如表3所示.PCSNN是基于度量學習的思想,衡量樣本對之間的相識性,是小樣本學習中的一個重要方法.如表3所示,在小樣本情況下,PCSNN的識別精度高于PCNN與MLP方法;同時,隨著樣本量的增加,PCSNN、PCNN、MLP的識別精度都有顯著的提升.這是由于深度學習方法容易受樣本量的影響,在小樣本情況下,PCNN與MLP學習效果不佳.隨著樣本量的增加,深度學習方法從數據獲取到更多的分類信息,從而提高了樣本的識別率.而本文提出的PCSNN將深度學習與度量學習的思想結合,利用深度學習方法提取數據特征,再利用孿生網絡的思想構建能夠度量樣本類別的多維空間,因此,隨著樣本量的增加,深度學習方法提取了更多的樣本特征信息,擴大了不同樣本間的空間距離,進一步提高了PCSNN的識別率. 表3 PCSNN與其他兩種方法測試結果對比 在多品種小批量的制造模式下,質量特征的改變主要體現在質量特征均值或方差的變化.為了驗證孿生網絡模型在不同品種下對控制圖的識別精度,本節使用PCSNN對A、B兩組質量參數變動的測試樣本進行識別. A組測試集的均值由46向54逐步遞增,方差為5,對應的PSCNN測試精度如表4所示.B組測試集的方差由3向7逐步遞增,均值為50,對應的PSNN測試精度如表5所示.分別對比表4與表5發現如下規律:1)在訓練樣本量相同的情況下,A1-A9或B1-B9的測試精度總體呈現‘峰形’,即測試樣本的均值或方差與訓練樣本的質量特征參數(μ=46,σ=5)相同時測試精度最高,測試樣本的測試精度隨著質量特征參數‘背離’訓練樣本質量特征參數的‘距離’增大而降低;2)絕大多數情況下,對于相同的測試集,隨著訓練樣本量的增加,測試精度逐漸增大;3)PCSNN在訓練樣本較少時,具有較高的識別率和較強的泛化能力. 表4 樣本均值變動下PCSNN測試結果 表5 方差變動下PCSNN測試結果 PCSNN將樣本特征映射到多維空間,通過算法迭代將相似樣本的空間距離縮小,擴大異種樣本的空間距離,從而構建了判斷樣本對是否相似的非線性映射,并通過One-shot8-way的方式,將待分類樣本與基于訓練集構建的支持集進行相似性判斷,實現樣本的分類.當控制圖樣本質量參數發生改變時,該控制圖樣本與訓練集樣本的相似性概率降低,但通過One-shot eight-way的方式,PCSNN選擇與訓練集最大相似概率的樣本分類作為待分類樣本的類別.因此,在控制圖樣本的質量特征參數發生變動時,PCSNN依舊保持較好的識別率. 本文提出的PCSNN模型,解決了在樣本量較少、識別類別較多時的基本控制圖模式識別問題.該網絡主要有兩個結構相同、權值共享的神經網絡構成,通過判斷控制圖樣本對是否相似,從而識別控制圖基本模式.通過使用不同樣本量的控制圖樣本,對MLP、PCNN、PCSNN進行訓練,分析了3個模型的測試精度,發現在控制圖的樣本較少情況下,PCSNN模型比MLP、PCNN模型展現出更高的識別精度;而隨著樣本量的增加,PCSNN的識別率也比MLP、PCNN高;通過質量特征參數變動下PCSNN測試精度對比實驗,發現在產品品種發生改變時,引發控制圖的特征參數變動的情況下,PCSNN展現出良好的泛化性能,對控制圖的模式識別表現出較高的識別率.3.2 多層感知器
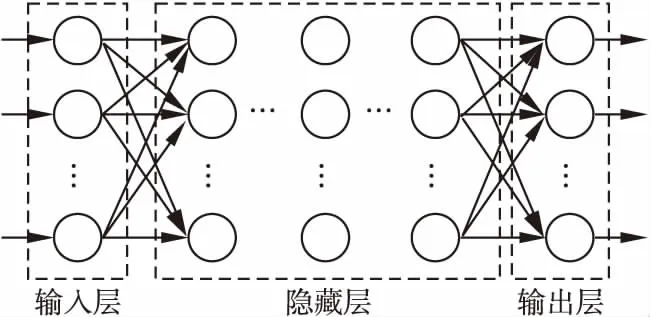
3.3 一維卷積神經網絡
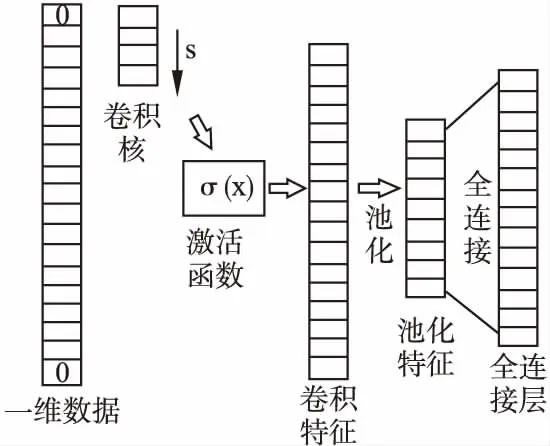
3.4 控制圖模式識別模型
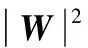
4 實驗驗證
4.1 實驗設計

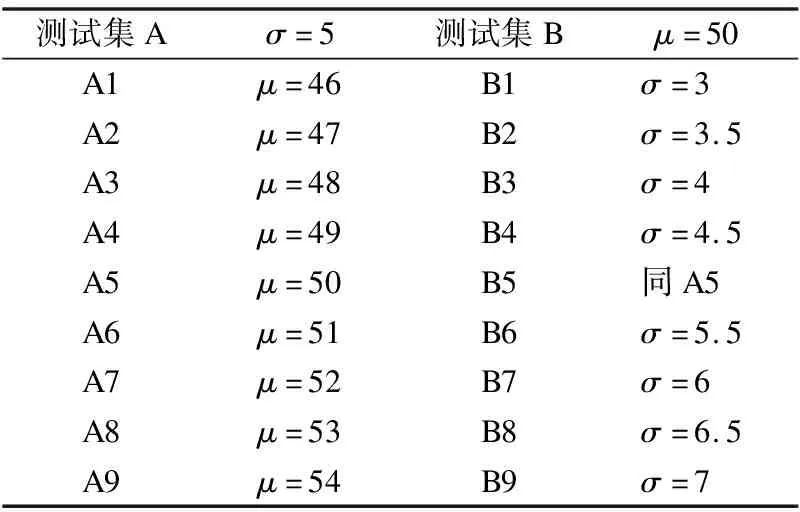
4.2 PSCNN與MLP、PCNN的對比實驗
4.3 質量特征參數變動下PCSNN測試精度對比實驗
5 總 結

