基于機械品質因數的全波壓電超聲換能器設計

胡 濤，劉 宇，傅 波

(四川大學機械工程學院，四川成都610065)

0 引 言

隨著科技的進步，制造方法也變得多樣化。相比于傳統的車銑刨磨等加工方式，超聲加工、電火花加工等特種加工方式能夠解決傳統加工方法難以處理的加工難題，在精密加工領域得到了廣泛的應用。作為超聲加工的核心，壓電超聲換能器的優化設計一直是研究的重點內容。目前壓電超聲換能器的常規設計方法是從四端網絡入手[1-4]，利用力電類比的方法，推導出復合變幅桿的等效電路圖，結合波動方程[5-8]，進行超聲換能器的設計和優化。這些設計方法主要針對半波壓電超聲換能器，對于全波壓電超聲換能器，各部分涉及的尺寸參數較多，頻率方程存在多值多解的情況，需要比較繁瑣的設計優化過程。本文從全波壓電超聲換能器的機械品質因數出發，預先設定一個符合實際要求的機械品質因數，減少尺寸變量。通過換能器等效點處的等效電路和等效質量推導計算機械品質因數的公式，結合機械品質因數和頻率方程的等高線圖，更加快捷合理地設計全波壓電超聲換能器各部分尺寸。

1 全波壓電超聲換能器的頻率方程及等效電路

常見的全波壓電超聲換能器的結構如圖 1所示，后蓋板為圓柱形，前蓋板由變截面階梯圓柱及末端錐形工具頭組成。其前蓋板的長度可按照半波長規律延長，圖中虛線部分表示全波長超聲振子的振動位移示意圖(①、②為節面)。為保證壓電超聲換能器在工作時能量損失盡可能小，在實際使用時通常在節面位置進行裝夾。如圖1所示，為保證裝夾的可靠性和穩定性且不失一般性，在對該結構的壓電超聲換能器進行設計分析時，如果第m段的材料為壓電材料，此時變幅桿包含兩段階梯，節面處于壓電陶瓷晶堆的中部；如果將該段的材料定義為前蓋板的材料，則此時前蓋板包含三段階梯，其節面位置位于壓電片與前蓋板的貼合面處。

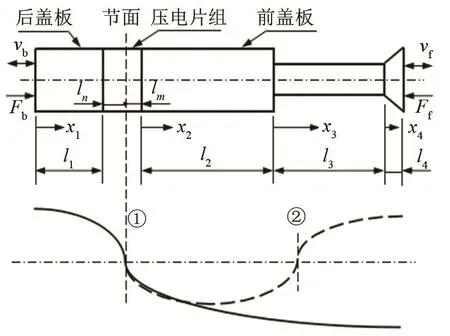
圖1 全波壓電超聲換能器結構及振動位移示意圖Fig1 Structure and displacement diagrams of full wave ultrasonic transducer

根據現有的壓電基礎理論及連續性桿的基本幾何方程、物理方程及平衡方程，可以快速得到壓電超聲換能器圓柱段的波動方程[8]。方程通解的實數部分為

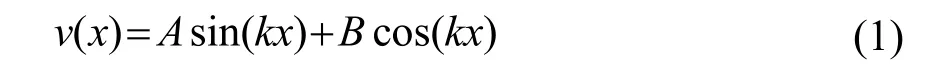
式中：A、B為壓電超聲換能器圓柱段振速的待定常數；k為波數。當代入各段(后蓋板、前蓋板、壓電晶片)的尺寸參數，利用結合面的速度與力的邊界條件即可求得相應的常數 A、B。由振速(其中為振動位移復變量)，聲阻抗Z=ρcS，可得到力F的表達式：

式中：E為彈性模量；S為截面積；ω為振動角頻率；c為聲速。

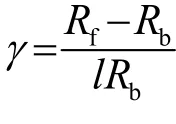
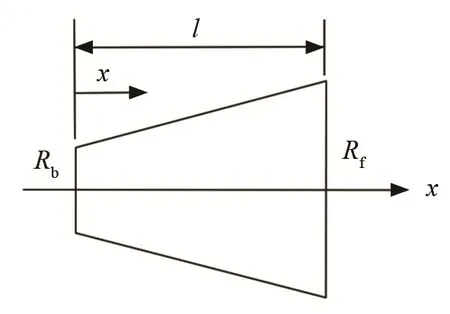
圖2 圓錐形變幅桿結構示意圖Fig.2 Structural diagram of conical horn

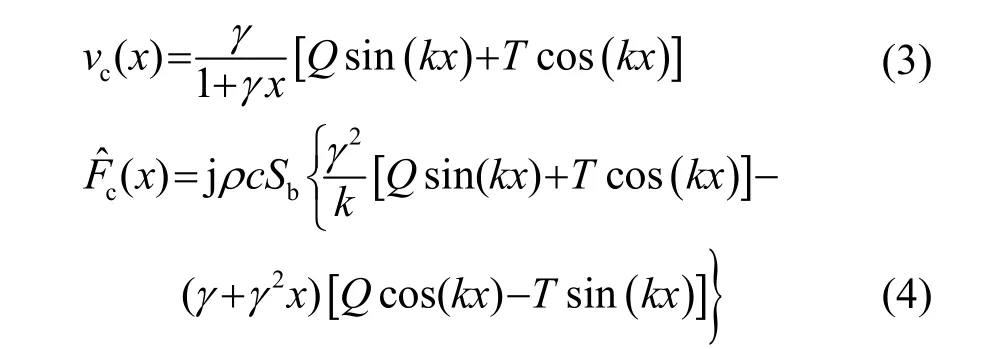
1.1 全波壓電超聲換能器節面左半部分的振速及頻率方程

如圖1所示，分析節面左半部分的1/4波長的組件，在理想情況下壓電超聲換能器各組件貼合面處力F與速度v是連續的，末端一般處于空氣中，可認為后蓋板的負載阻抗為零；若分別以各振動單元左端點為坐標零點，其邊界條件可表示為

由式(5c)及式(2)可得 1/4波長超聲振子的頻率方程：

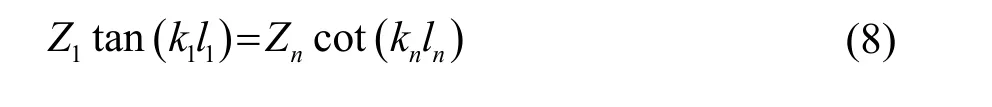
1.2 全波壓電超聲換能器節面右半部分的振速及頻率方程

如前所述，若分別以各振動單元左端點為坐標零點，由壓電超聲換能器組件之間的貼合面處力F與速度v的連續性可知，各組件之間的邊界條件為

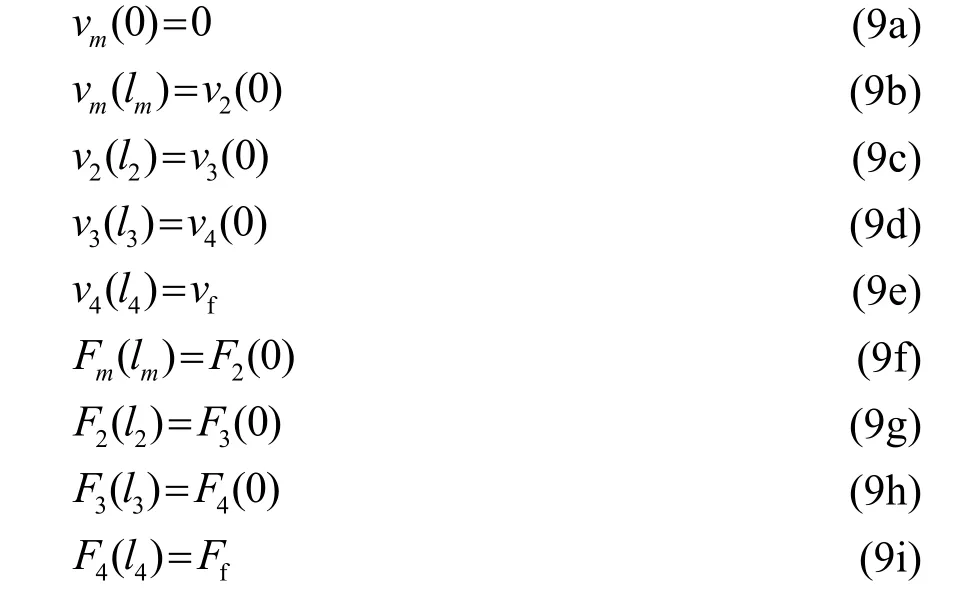
式中：vf為壓電超聲振子前蓋板末端的輸出振速，Ff為前蓋板末端的輸入力阻，在實際應用中Ff的值難以測量或估計，工程設計時通常用壓電超聲換能器處于空氣中的頻率方程計算尺寸參數，在后期的優化設計中對其加以調整即可達到使用要求，故此處取 Ff= 0。利用式(9a)～(9h)計算出節面右半部分的各段的振速與力的待定參數，節面右端各段的振速可表示為

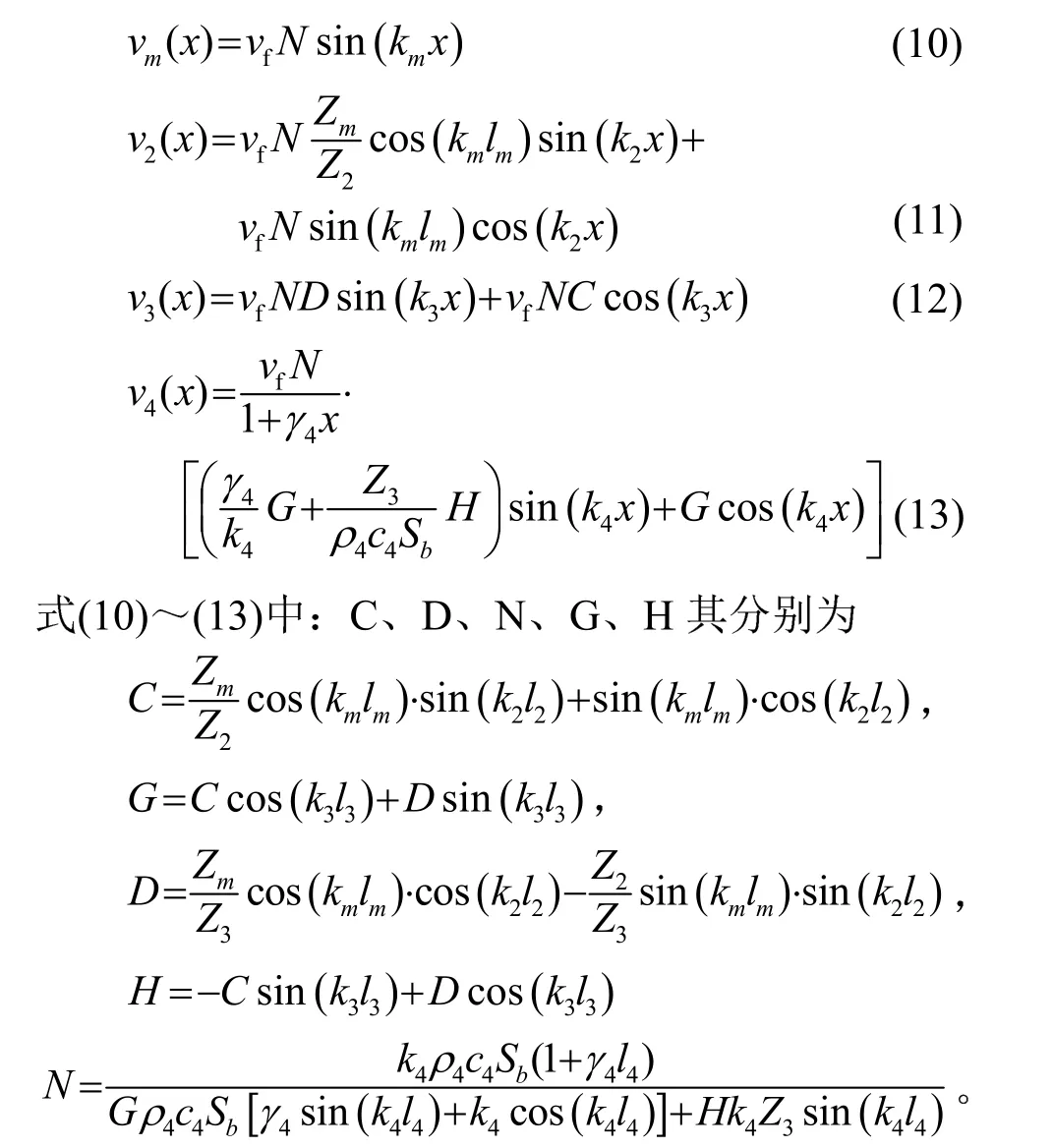
與全波壓電超聲換能器節面左邊的1/4波長振子類似，需要推導出對設計計算有實效的頻率方程，將以上各式代入式(9i)，經過運算與化簡，可計算出全波超聲換能器節面右邊部分頻率方程：

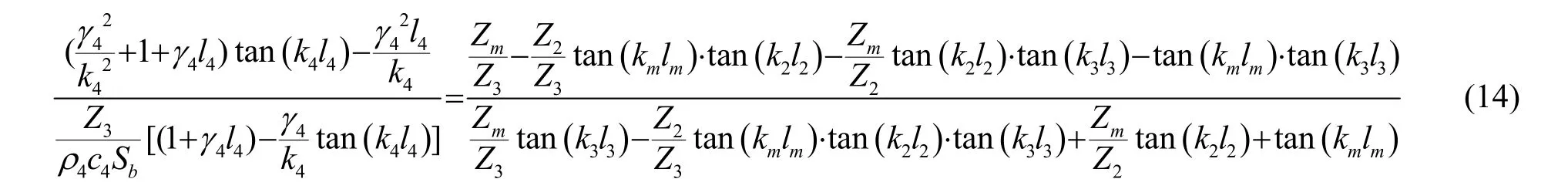
1.3 全波壓電超聲換能器等效電路及特性參數

1.3.1 前、后蓋板圓柱部分的等效電路

前、后蓋板的等效電路[9-10]可以很容易由機械桿的串聯四端網絡推導出。圖3為圓柱型桿的四端邊界條件，等效電路如圖4所示，圖中等效參數的具體表達式為

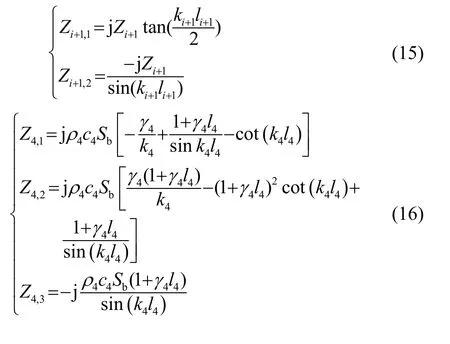
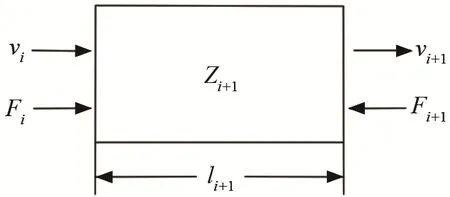
圖3 前、后蓋板中圓柱部分邊界條件示意圖Fig.3 Schematic diagram of boundary conditions of cylinder part in front and rear cover plates

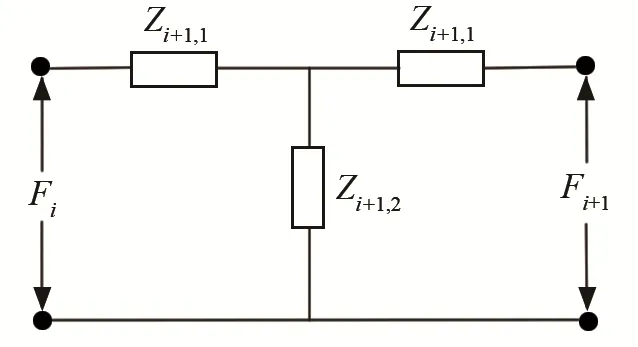
圖4 前、后蓋板中圓柱部分的等效電路圖Fig.4 Equivalent circuit diagram of cylinder part in front and rear cover plates

1.3.2 前蓋板圓錐部分的等效電路

前蓋板中圓錐部分的機械四端邊界條件與圓柱部分相同，如圖5所示。等效電路可表示為6所示，相關參數為

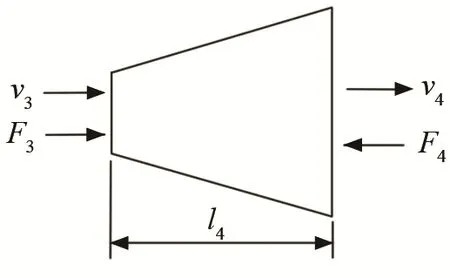
圖5 前蓋板中圓錐部分邊界條件示意圖Fig.5 Boundary condition diagram of cone part in front cover plate

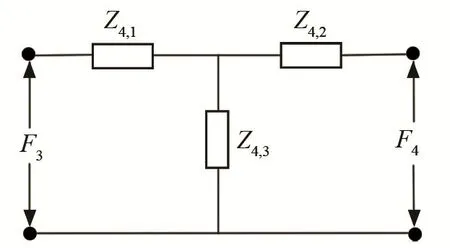
圖6 前蓋板中圓錐部分的等效電路圖Fig.6 Equivalent circuit diagram of cone part in front cover plate

根據本文所分析的全波壓電超聲換能器結構，可得其等效電路如圖7所示。

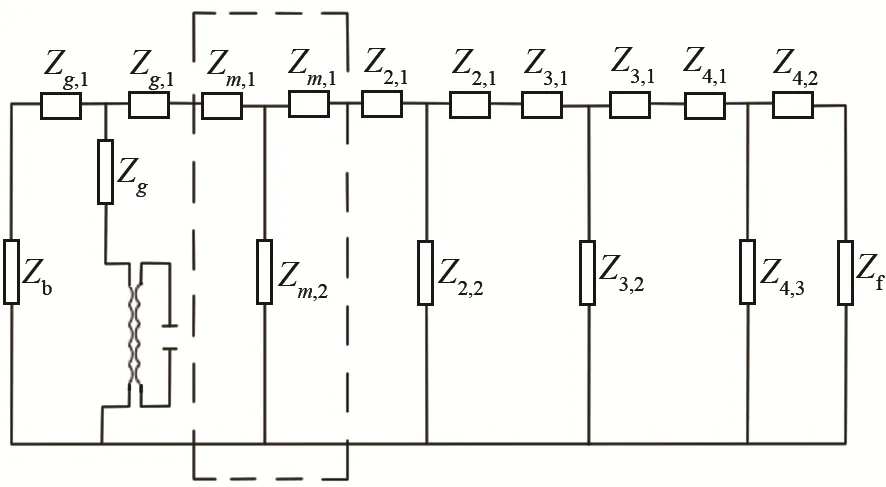
圖7 壓電超聲換能器的等效電路Fig.7 Equivalent circuit of piezoelectric ultrasonic transducer

Zb為壓電超聲換能器后蓋板輸入阻抗，Zf為前蓋板負載阻抗，當壓電超聲換能器應用于大功率場合時，其負載阻抗不可忽略。當后蓋板處于空氣中時，Zb可表示為

2 全波壓電超聲換能器的機械品質因數

由波動理論可知，當工作頻率等于壓電換能器的固有基波特征頻率時，整個壓電換能器即達到諧振狀態。如果在諧振頻率附近推算壓電超聲換能器的動態機械阻抗，并將此與同等狀態下的LC串聯電路比較，在一級近似的條件下，壓電換能器的等效質量可以等效為LC串聯電路中的電感，壓電超聲換能器的機械品質因數[10]可表示為

式中：ωs為壓電超聲換能器諧振狀態下的角頻率，Me為等效質量，Re為壓電超聲換能器換算到參考點的等效機械阻。以下利用前面的頻率方程和傳輸矩陣，推導出全波壓電超聲換能器機械品質因數的具體表達式。

2.1 全波壓電超聲換能器等效質量的計算

由能量等效原理可知，壓電超聲換能器在參考點處諧振時的等效質量Me滿足如下關系式：

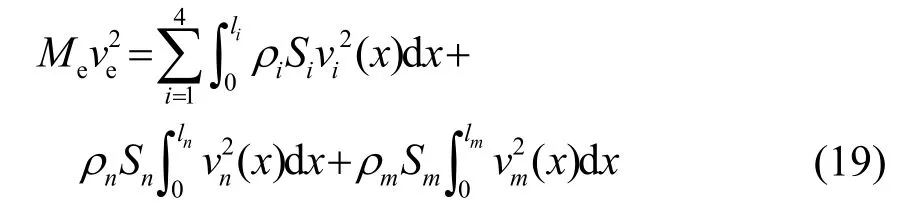
式中：ve為參考點的振速；S為壓電超聲換能器各組成部分的橫截面積。由節面處力的連續性可得力連續方程：

為了保證壓電超聲換能器在整個振動系統中的振動特性及阻抗匹配，一般，故式(20)可表示為

將式(6)、(7)及式(10)～(13)代入式(19)，并由力的連續方程可得壓電超聲換能器在參考點處的等效質量：

2.2 全波壓電超聲換能器等效阻抗的計算

壓電超聲換能器相對應的等效機械阻需要選定在等效質量同一參考點。如圖8(a)所示，現考慮前蓋板輸出端處于空氣中的負載阻抗，并根據圖 7所示的等效電路圖將末端的等效負載阻抗等效到前蓋板的所有階梯變截面處，如圖8(b)、8(c)、8(d)、8(e)所示。

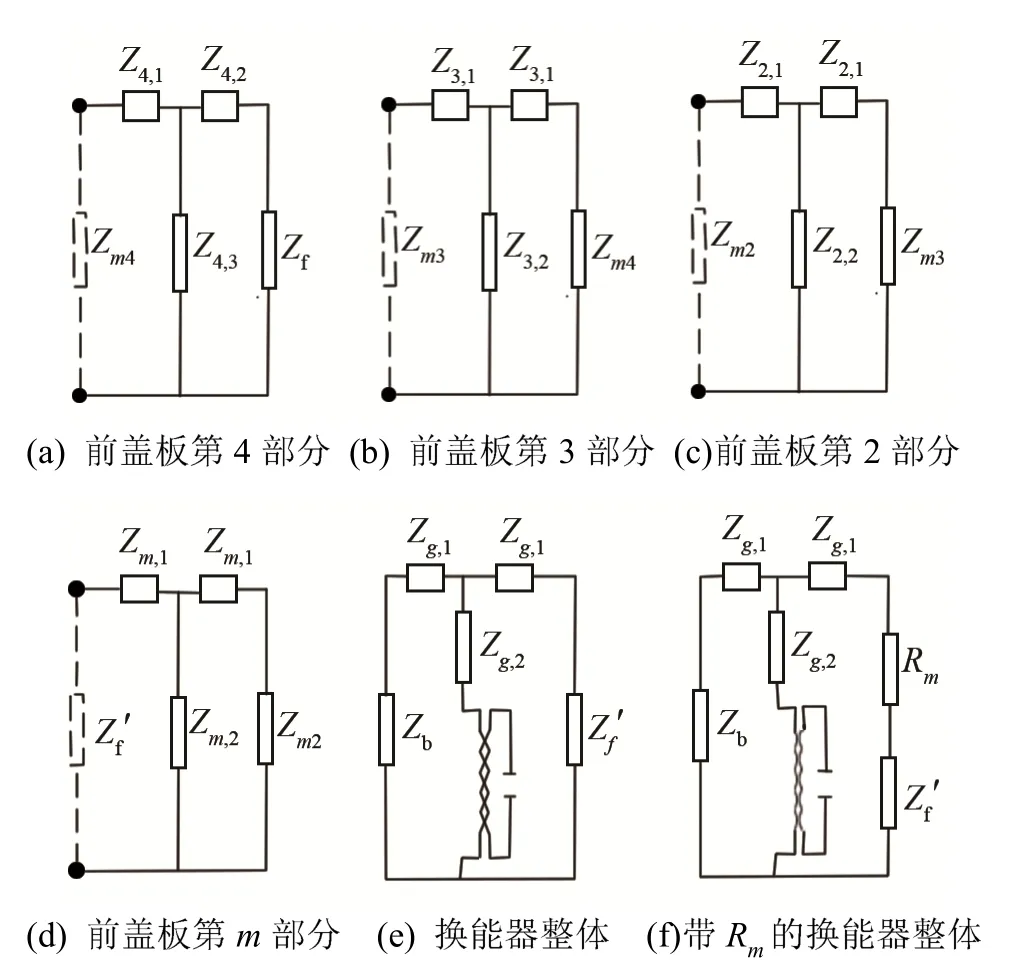
圖8 等效阻抗圖Fig.8 Equivalent impedance diagram

圖8中Zm4、Zm3、Zm2、Zf′分別表示前蓋板第4部分、第3部分、第2部分、第m部分等效的輸入阻抗(包括負載阻抗與材料特性阻抗的總和)，經過簡單的運算，各等效點的等效輸入阻抗為

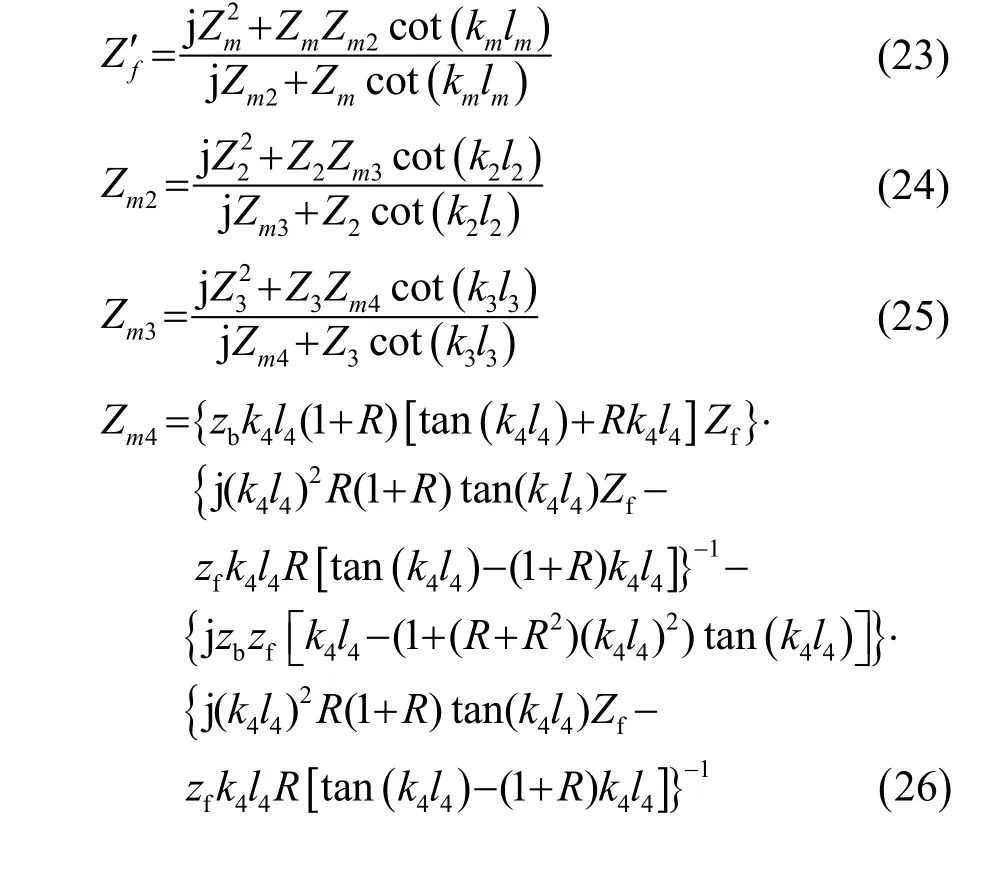
若考慮電能損失和壓電超聲換能器的結構阻尼，則需在壓電陶瓷晶堆端面的等效阻抗上串聯一個損耗電阻Rm，如圖8(f)所示；同時，壓電陶瓷片端面所受的來自前蓋板、變幅桿、工具頭及負載的總等效輸入阻抗可表示為為等效輸入電阻，Xf為等效輸入電抗。

2.3 等效點的選取

在以往的研究[11]中，為了方便計算，等效點一般選定在壓電超聲換能器前蓋板與壓電片貼合面處，本文選定前蓋板階梯變幅桿小圓柱部分中部的振速為參考點振速ve，依據式(12)，第3段中點的參考振速為

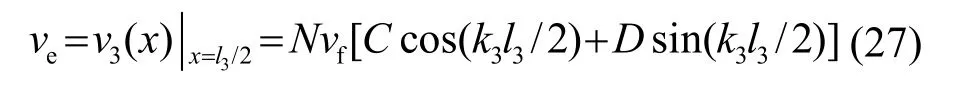
利用電路等效原理將末端的負載阻抗Zf等效到l3的中點處，將式(26)代入式(25)，并對結果進行分母有理化，由于負載阻抗中電阻部分的存在，才會使得在電壓作用部分電能轉換為熱能，所以將表達式的分子中帶有虛數單位的項去掉，從而可以得到等效到l3中點處的負載電阻，經過化簡有：

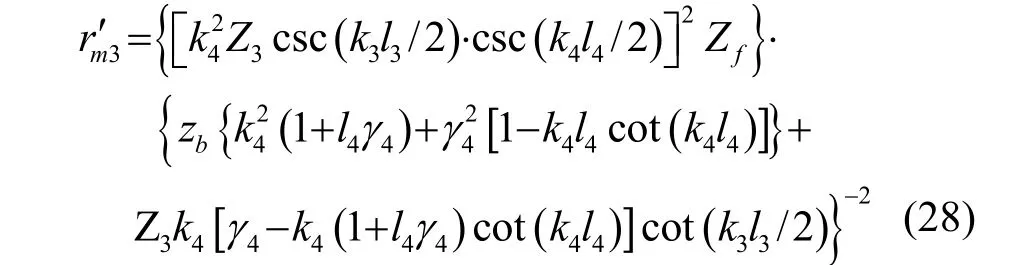
由式(28)可知，當電抗分量的尺寸參數確定后，等效到前蓋板第3段中點的等效負載阻抗Zm3與末端的輸入負載阻抗Zf成正比，所以在利用超聲換能器的機械品質因數QM對其尺寸進行優化設計時可以不用將輸入的負載阻抗計算在內，即只考慮壓電超聲換能器各部分尺寸參數對其機械品質因數的影響即可。

將式(27)、式(28)代入式(18)，可以得到整個全波壓電超聲換能器的機械品質因數的表達式為

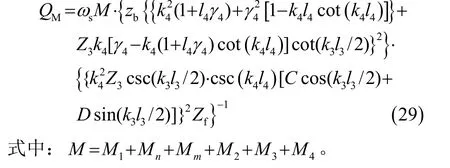
3 基于機械品質因數的全波壓電超聲換能器設計算例

以應用較廣泛的功率為 200 W、諧振頻率為28 kHz、結構如圖1所示的全波壓電超聲換能器為例，具體闡述本文所提出的設計方法。考慮一般的應用環境，采用規格為?20×?8×6 mm的PZT-8圓環形壓電片。

當壓電超聲換能器的功率、壓電片材料及規格確定后，可利用式(30)計算出所需的壓電片片數：

式中：n為壓電片數量；P為壓電超聲振子的輸入功率；U為壓電片的功率容量，通常取 2～3 W·(kHz·cm3)-1；f為壓電超聲振子的諧振頻率。故所需的壓電片片數為

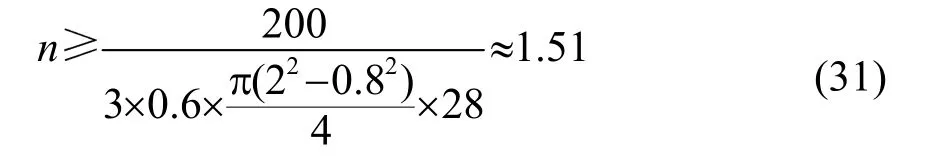
將計算結果取整數，即壓電片片數應選擇2片。壓電超聲換能器各組件的材料及屬性匯總如表1中所示。

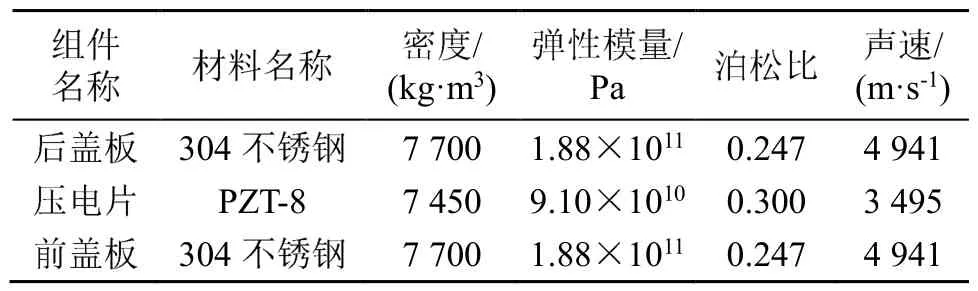
表1 壓電超聲換能器各組件材料及屬性Table 1 Properties of components’ materials of ultrasonic transducer

利用1/4波長超聲振子的頻率方程(8)對后蓋板進行設計計算，式中k1、kn為已知量；為保證在預緊螺栓的預緊力作用下壓電片整個端面能被后蓋板壓緊，一般取后蓋板的直徑與壓電片直徑相同，即R1=Rn=1 0 mm，將材料的特征參數值代入式中，即可求得超聲振子后蓋板的長度。本文中的超聲換能器的后蓋板模型采用第1階縱振模態，故所求得的后蓋板長度l1=22 mm。由于壓電片規格已選定，依前述有：Rn=10mm。

為了簡化模型，按照換能器傳統結構，將節面設定在壓電片與前蓋板的接觸面處，故在后續的優化設計中，將圖1所示結構的m段視為前蓋板。由于喇叭狀工具頭很小，相比于整個壓電超聲換能器的總等效質量，其占比很少，為了簡化計算，可以用工具輸入端的振速代替整個工具頭的振動速度，同時將喇叭狀工具頭等效為底面面積與工具頭中部橫截面面積相等的圓柱體，并利用動量守恒原理可計算出喇叭狀工具頭的等效質量：

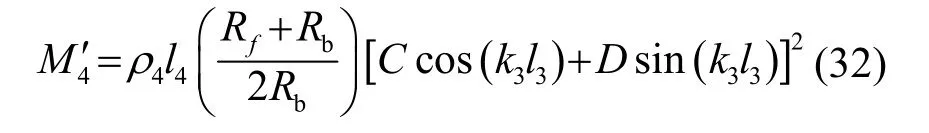
稍加推導即可求得整個壓電超聲換能器機械品質因數QM的關系式，具體顯示表達式詳見附錄I。算例中全波壓電超聲換能器的結構較復雜，依據其結構特點及應用場合對其結構做出了適當簡化，并事先確定部分尺寸參數，如表2所示。

表2 壓電超聲換能器各部分已確定尺寸參數Table 2 The size parameters of each part of piezoelectric ultrasonic transducer

從表2中可見：本例中第m段的長度lm、第2段的長度l2與半徑r2、第3段的長度l3為未知參數。整個全波壓電超聲換能器的QM可表示為

由于該關系式比較復雜，甚至很難利用計算機直接進行求解，本文提出了如下的前蓋板設計計算方法：為了減少設計時不必要的計算分析，可以在某一特定機械QM值時，利用等高點的方式給定r2、l2的值繪出lm、l3的尺寸變化關系圖，與此同時繪制出在該條件下所對應頻率方程等于零的等高點曲線，通過比較兩等高點曲線，即可確定該特定尺寸r2、l2下是否存在lm、l3的優質解，并可較準確地確定相應的尺寸參數。該方法是一種降維分析方法，回避了解QM方程、頻率方程的繁瑣過程(由于存在多值多解，有時利用計算機都無法求解)，對于求解此問題是極為有效的。

以r2=5 mm、l2=30 mm為例說明等高點法優化設計的過程，此時壓電超聲換能器前蓋板的頻率方程式(14)為lm、l3的函數，前蓋板的諧振條件為lm、l3滿足該頻率方程，故式(14)恒為0，利用此關系可以繪制出該頻率方程的等高曲線，同時也可以描述為壓電超聲換能器在諧振狀態下lm、l3的變化關系曲線，如圖9所示。理想的前蓋板優化設計需使所設計的振子具有較高的機械QM值，由于結構阻尼的存在，整個壓電超聲振子系統的機械QM值不會高于壓電材料的QM值，d33模式PZT壓電陶瓷材料機械品質因數的范圍一般為 500～1 000[9]，為此，先在式(33)中設定一個較為合理的QM值(可取1 000)，并以此函數繪制該QM值下lm、l3的變化關系曲線，即此狀態下的等高曲線，如圖10所示。

頻率方程反映的是壓電超聲換能器處于諧振狀態下其各振動元件尺寸應滿足的關系，由波的傳導理論知，諧振振動元件沿其軸向可能有多個振幅為0的點，即相對應多個節面位置，所以頻率方程也包含了該關系，圖9中所顯示的就是一階縱振、二階縱振狀態下lm、l3應滿足的關系。結合圖 9、圖10可得圖11。由圖11可知，頻率方程等高曲線與品質因數等高曲線若有交點則為優值點，結合QM函數等高曲線中的極值區，若該lm、l3在該點附近區域內取值時，所設計的壓電超聲換能器機械QM值都將比所選定的值大，則取交點附近一段區域為優值區間，頻率方程等高曲線若與品質因數等高曲線沒有交點，說明在該特定尺寸r2、l2下，lm與l3取值不能同時滿足所需機械品質因數和頻率方程，則盡可能取兩曲線最為接近的點選取優值區間。優值區間的確定，縮小了Mathematica程序求解頻率方程的搜索區間，提高了計算的效率和準確性。

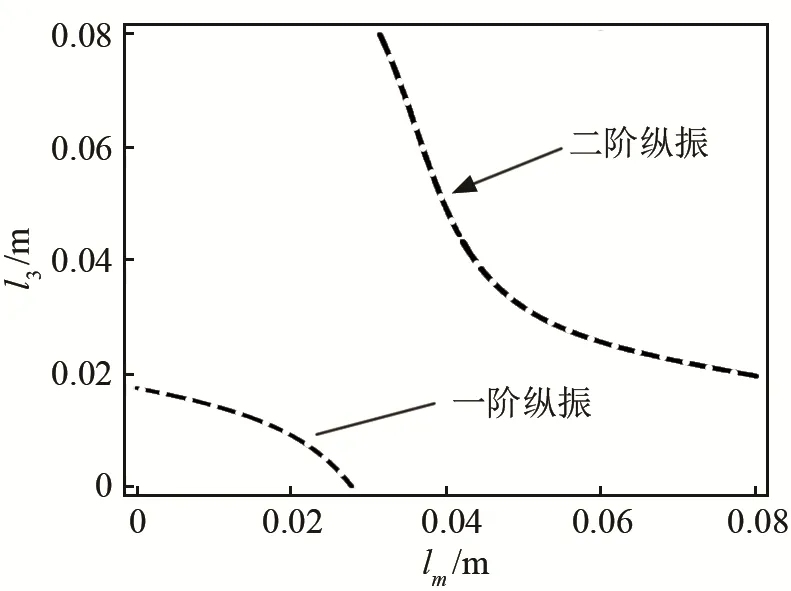
圖9 頻率方程等高曲線Fig.9 Contour curve of frequency equation

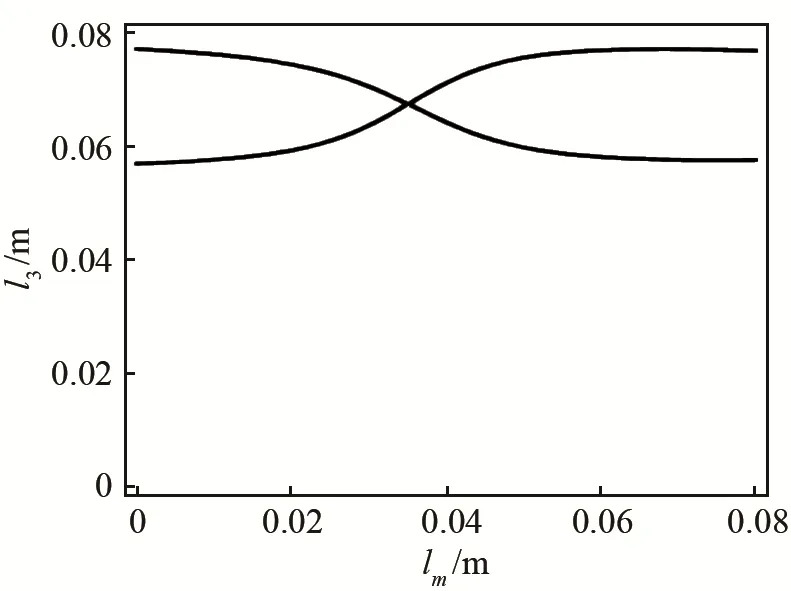
圖10 QM函數等高曲線Fig.10 Contour curve of QM function

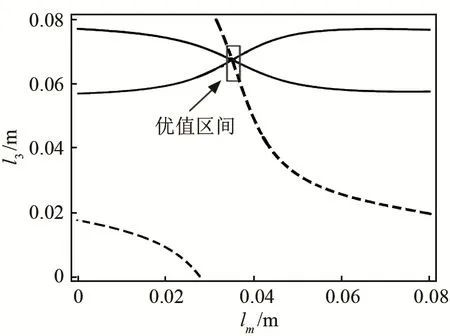
圖11 頻率方程和QM等高線混合圖Fig.11 Mixed graph of frequency equation and QM contour

利用以上方法，求得了幾組優質參數值，如表3所示。

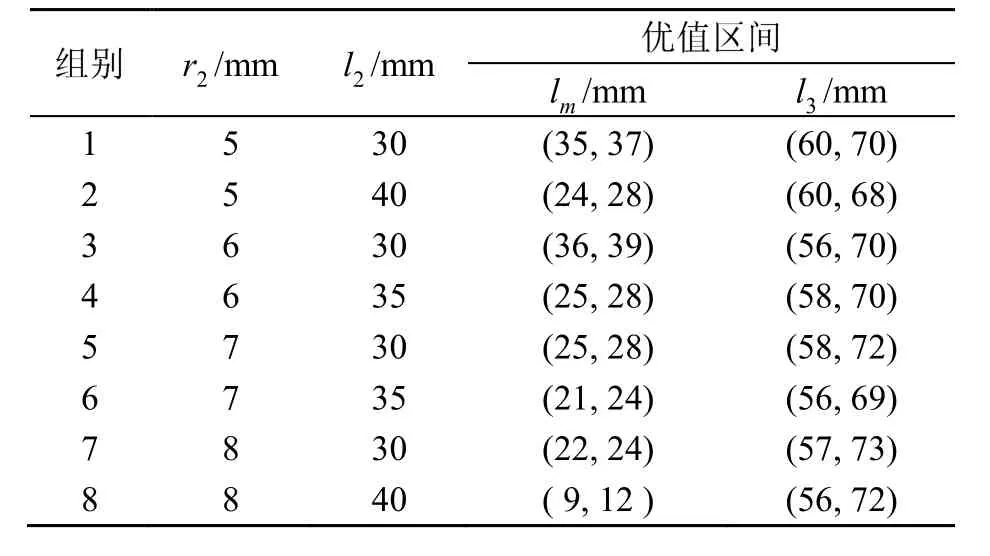
表3 前蓋板尺寸的優值區間Table 3 Optimal value range of front cover plate sizes

4 仿真分析

依據表 3，分別選取算例模型前蓋板優化后的幾組特定r2、l2尺寸以及相應的lm或l3的優值，利用頻率方程式(14)分別計算出l3或lm的長度值；利用所得全波壓電超聲換能器的所有尺寸參數在SolidWorks軟件中建立其前蓋板、壓電片、后蓋板的零件模型并將零件進行裝配，從而得到整個換能器的裝配體模型；將模型導入 ANSYS Workbench軟件中進行模態分析，求取特定縱振模態下壓電超聲振子的特征頻率，與設計頻率28 kHz對比分析，驗證本文所建議的優化設計方法的可行性。

為了使三維建模軟件與建立頻率方程時的模型具有良好的一致性，壓電片、后蓋板、前蓋板分別采用實心結構。以r2=5 mm、l2=30 mm為例，參照表 3中lm的優值區間，選取lm=36 mm，在Mathematica軟件中利用頻率方程(14)求解l3的長度，依據實例模型可知此時l3的長度應為64 mm。

依據上述方法選取了8組模型，并分別通過頻率方程式(14)計算得到l3的值，將所有模型的尺寸參數列于表4中。

以1號模型振子為例，經ANSYS Workbench軟件分析，其振動模態分析結果如圖12所示。

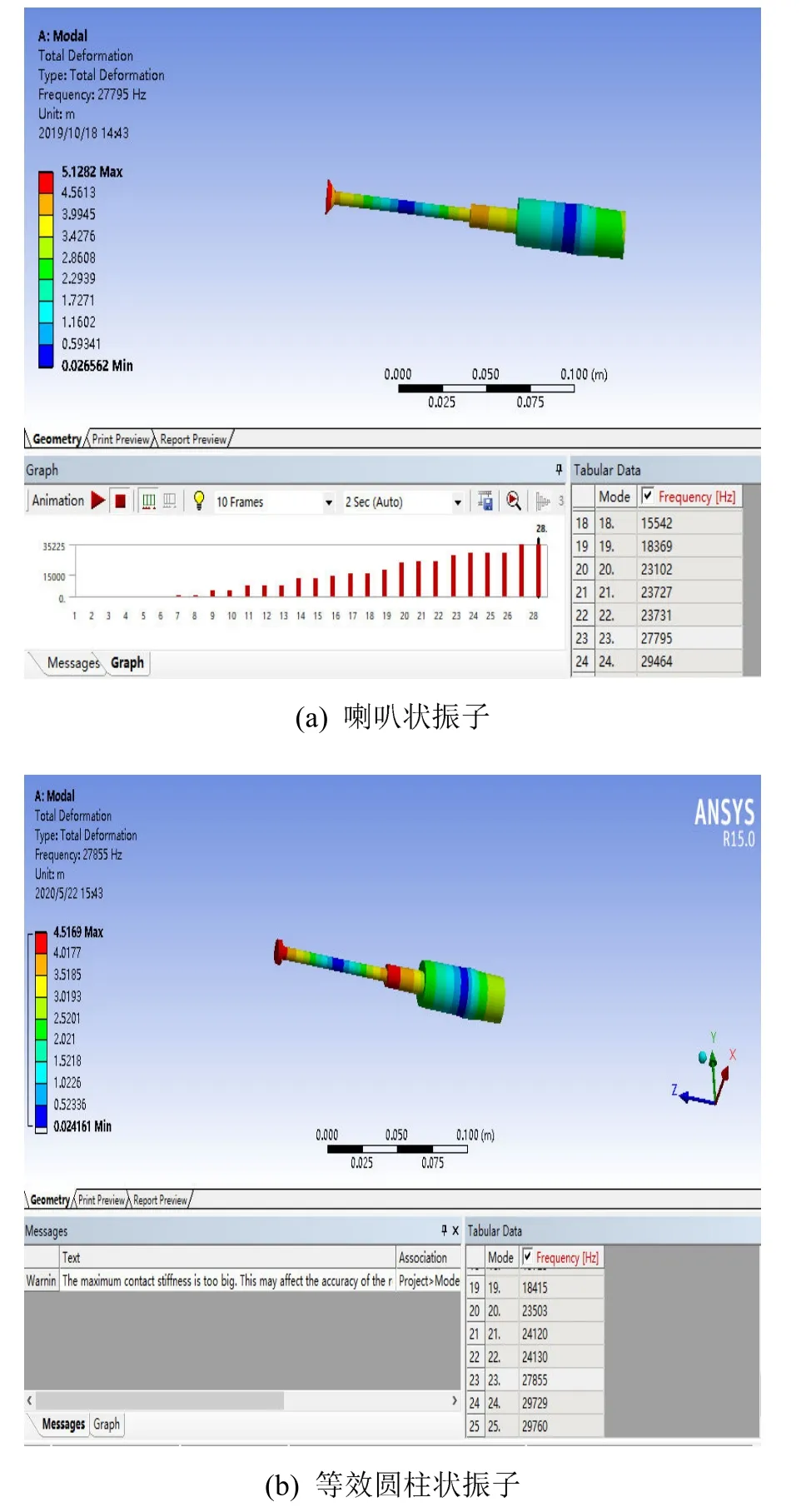
圖12 壓電超聲換能器1號模型縱向模態振動云圖Fig.12 Cloud chart of longitudinal mode vibration of Model 1

從分析結果中可見，該壓電超聲換能器模型在第 23階模態為縱振模態，節面位置處于壓電片與前蓋板貼合面位置附近，喇叭狀振子諧振頻率為27.795 kHz，等效圓柱體工具頭振子諧振頻率為27.855 kHz，兩者誤差率為0.2%，符合工程上等效處理要求，且與其設計節面位置和設計頻率28 kHz均具有良好的一致性；諧振頻率與其前后振動模態的頻率相隔較遠，具有較大的頻帶寬，在使用中可以避免其他振動形式的干涉。建立表4中所有對照組的裝配體模型，對其進行模態分析并提取其第二階縱振模態下的諧振頻率，結果如表5所示。

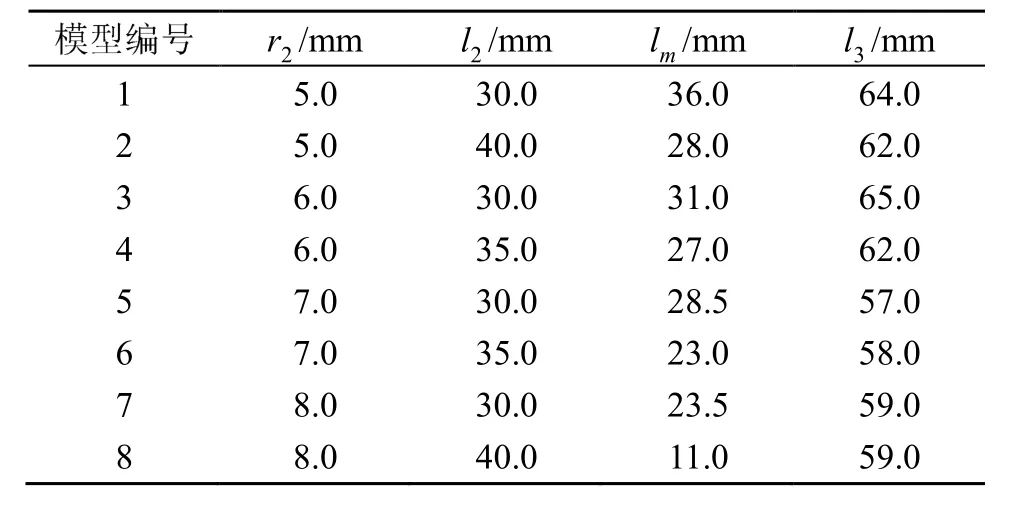
表4 壓電超聲換能器8組模型的前蓋板尺寸參數計算值Table 4 Calculated size parameters of front cover plate for 8 model groups of piezoelectric ultrasonic transducer

由表5中數據可知，利用本文方法計算獲得的全波壓電超聲換能器尺寸，其模型諧振頻率的仿真值略低于設計頻率。其原因可能為仿真模型在其特征縱振模態處也包含了其附近的振動模態，只是其縱振振動位移占據了其總位移的絕大部分，而在理論推導中并未考慮不同振動方式相互疊加與耦合的情況，只考慮僅存在沿一維桿軸向的振動，導致了軟件仿真值與設計值之間存在誤差。從8組模型諧振頻率的仿真值可以看出，其大小均與設計值28 kHz很接近，最大差值為 500 Hz，最小差值為200 Hz，與實際情況符合良好，設計中對計算出的模型尺寸參數稍加調整(適當減小l3)或直接作為實際模型的尺寸值即可，可以提高該類型壓電超聲換能器的設計效率。

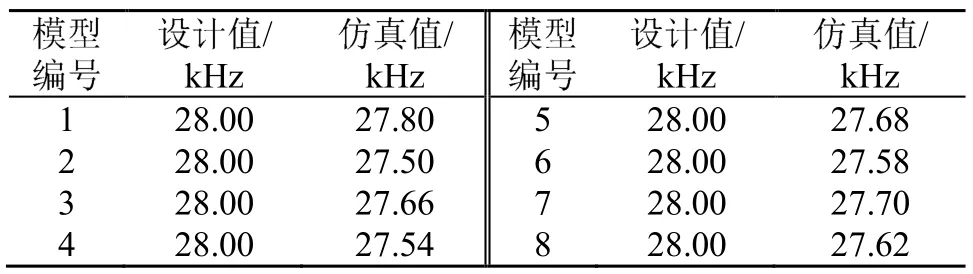
表5 8組模型諧振頻率計算值與仿真值對照表Table 5 Comparison table of calculated and simulated resonance frequencies for the 8 model groups

在壓電超聲換能器的設計過程中，也可以直接固定節面位置在壓電片與前蓋板接觸處，簡化設計參數，將前蓋板三段階梯桿變為兩段更易滿足設計要求，也可以引入階梯段的放大系數作為新的參考量，對階梯段的各段尺寸進行限制。

5 結 論

本文針對全波壓電超聲換能器結構復雜，其頻率方程存在多值多解的情況，提出了一種基于機械品質因數關系式的全波壓電超聲換能器結構優化設計方法，在壓電超聲換能器的頻率方程和等效電路圖的基礎上，推導出與其各個組件尺寸參數相關的壓電超聲換能器機械品質因數的表達式，結合圖解法、等高點法得到模型結構尺寸參數的優值區間，進而利用Mathematica程序求解頻率方程得到壓電超聲換能器的結構尺寸。利用有限元軟件ANSYS對該尺寸的全波壓電超聲換能器進行了模態分析，仿真分析得到的諧振頻率與設計頻率的誤差很小，驗證了本文所建議的全波壓電超聲換能器結構設計方法的合理性，為全波壓電超聲換能器結構優化設計方法的研究提供參考。

附錄I

壓電超聲振子的機械品質因數的計算公式：