陸地靶場聲定位系統(tǒng)布站圖形優(yōu)化方法
于國棟,王春陽,張 月
(63850部隊,吉林白城137001)
0 引 言
陸地靶場試驗中,精確的測試結果對于武器裝備的評定起著至關重要的作用。隨著測試系統(tǒng)數(shù)量的增加和復雜性的提高,合理使用測試設備顯得格外重要。
目前,利用聲定位技術測量落點坐標的相關設備已在陸地靶場驗收,并取得較好的效果。決定設備能否發(fā)揮其最大效能,主要取決于兩個方面:高效的數(shù)據處理方法[1]和高質量的布站陣形結構[2]。自設備投入使用以來,經過不斷研究探索,已總結出很多有價值的成果[3-6]。但查閱國內外文獻后發(fā)現(xiàn),目前針對聲學設備布站陣形結構的研究成果較少,大多數(shù)基于光學設備和定位導航設備,只有文獻[2]中有關于聲定位設備布站陣形結構對定位精度影響的論述,但并未總結出度量布站陣形結構優(yōu)劣程度的方法。
陸地靶場的聲定位設備需要在彈丸落區(qū)周圍布設一些探測器,來接收彈丸落地時產生的聲信號。對信號進行處理,提取出爆炸信號到傳感器間的時延差作為觀測值,進行解算可以得到彈丸的落點坐標。根據聲學設備的特性及使用方式,優(yōu)化其布站陣形結構通常需要從兩個方面進行考慮:探測器陣列的布站陣形和探測器的數(shù)量。合理的布站陣形可有效提高設備的測試精度及可靠性;除布站陣形外,探測器數(shù)量也會對測試結果產生一定的影響,使用過多的探測器,并不會明顯提高測試精度,反而降低了系統(tǒng)的使用效率。
為能有效提高陸地靶場聲定位系統(tǒng)的測試精度和使用效率,本文提出了一種布站陣形結構優(yōu)劣的度量方法,并通過計算仿真數(shù)據和試驗數(shù)據,驗證了該方法的有效性和可行性。
1 原 理
1.1 聲源定位原理及算法
聲源三維坐標為(x, y, z),需要布設3個以上探測器才能得到聲源的位置,設探測器數(shù)量為 n。如圖 1所示,各探測器位置分別為(x1, y1, z1),為探測器接收到聲源信號的時刻。以t1為基準,其他時刻與t1的差為Δ t12,Δt13,…,Δt1n,聲速為c。
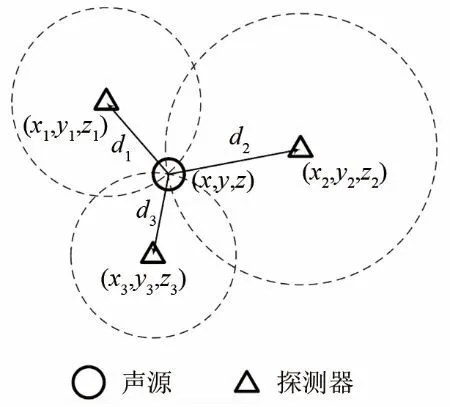
圖1 聲定位原理示意圖Fig.1 Principle diagram of sound positioning
根據探測器與聲源的幾何關系,可構造如下誤差函數(shù):


由于陸地靶場試驗場地較平坦,彈丸落點的高程與探測器陣列的高程差異較小。因此,文章中對布站陣形的分析均是基于二維平面,無高程元素,但計算方法相類似,不另做分析。
1.2 布站陣形結構優(yōu)劣的度量方法

式中,λi為矩陣的特征值。當λi中有一個或者幾個接近于0時,則Ui(i = 1 ,2,m)接近0。
雖然Ui可以直接反映布站陣形結構的幾何特性,但不能確定陣形結構的優(yōu)劣。主要原因為:一是Ui的大小與向量模有關;二是 U沒有相對性。另一方面,對于觀測矩陣B∈ Rm×n,一般m> n,僅考慮m=n是不全面的。
對于觀測矩陣B∈ Rm×n,當m=n時,觀測矩陣B的行向量為則:

此時,所有向量的模一樣,U0為超平行多面體的最大體積,與理想結構下的超平行多面體體積相比,可作為衡量陣形結構優(yōu)劣的依據[9]。因此,設向量組中范數(shù)最大的觀測向量為b1,則:
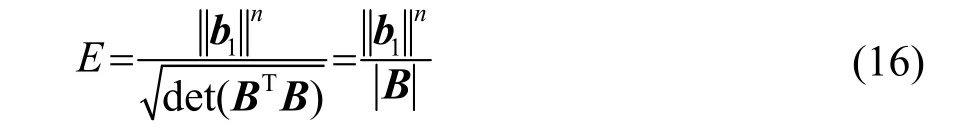
當m> n時,為了計算方便,B分解成 B = Q1G,Q1是正交列滿秩矩陣,G為行滿秩矩陣。矩陣 G的行向量為,設g1為范數(shù)最大的行向量,則:

可以看出,E的范圍為1≤ E ≤ ∞ 。顯然,Um越接近U0,即E越小,陣形結構越好,相反,E越大陣形結構越差。當 E大于一定界限時(界限值根據具體情況決定),說明探測器組成的陣形結構非常差,嚴重影響設備的測試精度,使得設備的測試結果變得不可靠。
2 仿真與分析
優(yōu)化布站方案通常從探測器組成的布站陣形和布設探測器的數(shù)量兩個方面來考慮。
適合陸地靶場應用的布站陣形,優(yōu)選有L型、U字型、||型、口字型、田字型五種,如圖2所示。

圖2 五種布站陣形示意圖Fig.2 Diagram of the five sensor layout patterns
2.1 布站陣形對觀測結構的影響
為比較上述五種布站陣形,模擬了一組數(shù)據,在0 < x < 2 000 m ,0 < y <2 000 m范圍內,以網格進行劃分,間隔10 m,網格交叉點處作為彈丸落點。五種圖形中探測器的位置如下:
(1) L型 : 范 圍 為 :300 m < x<1 700 m ,300 m < y<1 700 m,間隔100 m,共29個探測器。
(2) ||型 : 范 圍 為 :300 m < x<1 700 m ,300 m < y<1 700 m,間隔100 m,共30個探測器。
(3) U 型 : 范 圍 為 :300 m < x<1 700 m,300 m < y<1 700 m,間隔200 m,共22個探測器。
(4) 口 型 : 范 圍 為 :300 m < x<1 700 m,300 m < y<1 700 m,間隔200 m,共28個探測器。
(5) 田 型 : 范 圍 為 :300 m < x<1 700 m ,300 m < y<1 700 m,間隔200 m,共40個探測器。
對網格交叉點處的仿真落點進行計算,得到所有落點的E。再統(tǒng)計所有落點的E的平均值和均方差,結果如圖3和表1所示。
從圖3和表1可以看出,五種布站陣形的E值平均值無明顯差異,說明五種布站陣形對測試結果的影響無差別。但是,從E的均方差來看,田字型最優(yōu),L型最差,剩余三個圖形差異不明顯。出現(xiàn)這種情況的原因為:L型在控制區(qū)域的左上角、左下角及右下角結構較差,影響了其E的均方差;而田字型在x和y方向均有一定數(shù)量的探測器,并且這些探測器分布均勻,因此,即便有個別區(qū)域結構較差,也不會對E的均方差產生太大的影響。
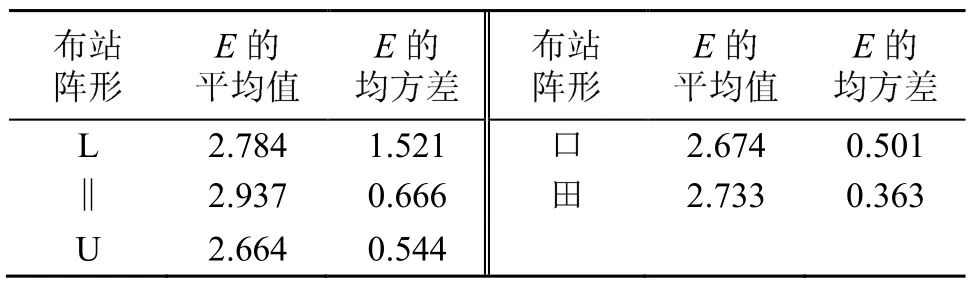
表1 五種布站陣形的仿真結果(整個區(qū)域)Table 1 Simulation results of five sensor layout patterns(whole region)
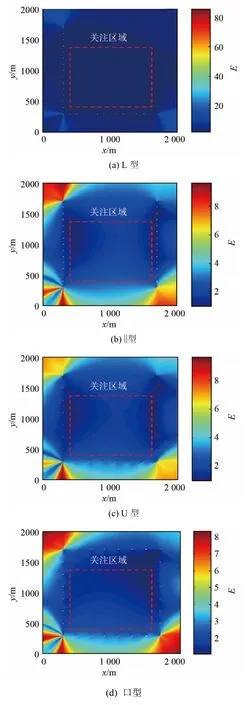
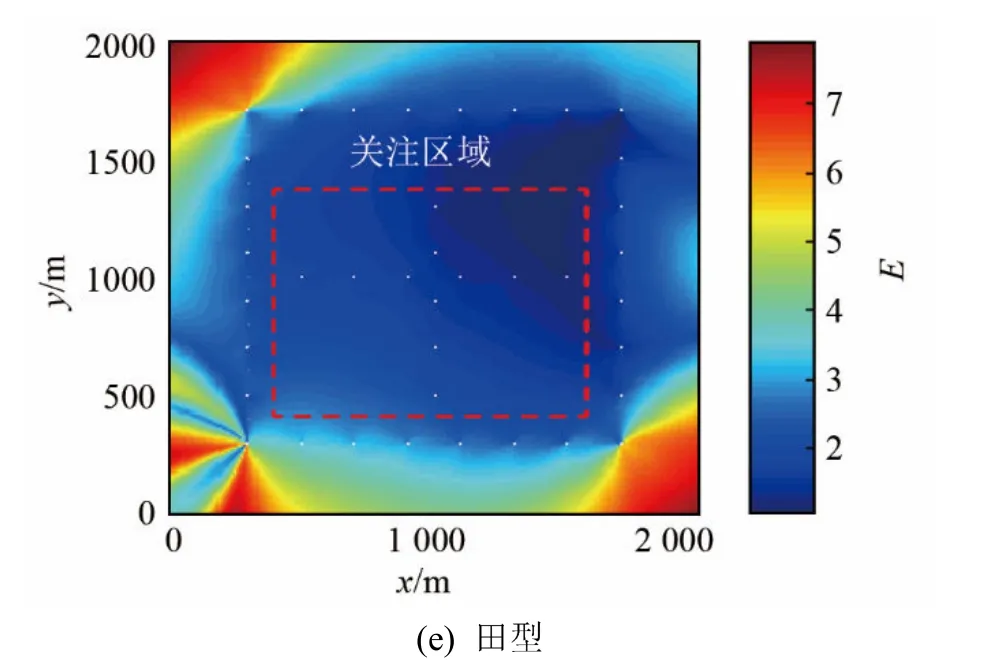
圖3 五種布站陣形的仿真結果Fig.3 Simulation results of five sensor layout patterns
陸地靶場試驗時,不需要對全部理論落區(qū)進行控制,往往存在一個關注區(qū)域,大多數(shù)彈丸會落入該區(qū)域,只有少數(shù)異常彈會出現(xiàn)在該區(qū)域之外,因此, 通常我們更關心關注區(qū)域處的測試精度。仿真試驗中,將400 m < x<1 400 m ,400 m < y <1400 m區(qū)域設定為關注區(qū)域。對關注區(qū)域內的落點進行計算,并統(tǒng)計E的平均值和均方差,結果表2所示。
從表2可以看出,L型最優(yōu),||型最差,剩余三種無明顯差異。出現(xiàn)這種情況的原因是:||型在 x方向上布設的探測器過少,因此在該方向上的結構較差,而其他四種圖形在x和y方向上均布設一定數(shù)量的探測器,因此,結構相對較好。從E的均方差來看,U字型和口字型結構變化較平穩(wěn),田字型結構變化較劇烈,出現(xiàn)這種情況的原因是,田字型中間添加的十字型影響了結構的連續(xù)性。
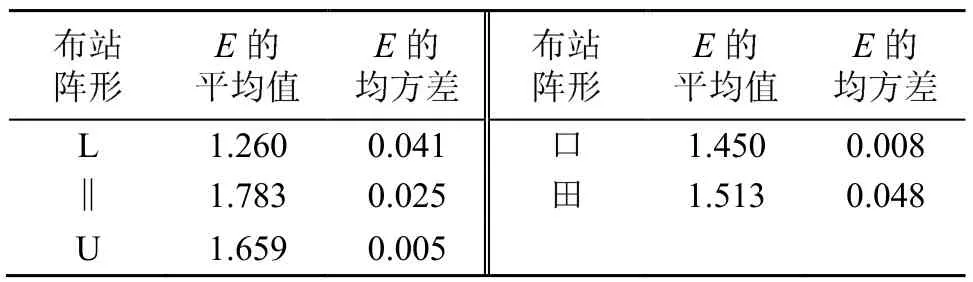
表2 五種布站陣形的仿真結果(關注區(qū)域)Table 2 Simulation results of five sensor layout patterns(region of interest)
通過上述分析,可以總結出如下結論:
(1) 布站陣形的選擇,需要根據試驗的具體情況決定。
(2) 布站方案傾向于考慮整個落區(qū)的觀測結構,盡量避免使用L型布站,推薦采用U字型、口字型、田字型;當傾向于考慮關注區(qū)域的觀測結構時,L型結構最好,||型最差,因此,盡量避免使用||型布站。
(3) 當落區(qū)環(huán)境較差,不易于布設過于復雜的圖形時,可選擇U字型或口字型。
2.2 探測器數(shù)量對觀測結構的影響
模擬一組數(shù)據,在0 <x< 2 000 m ,0 <y< 2 000 m范圍內,以網格進行劃分,間隔10 m,網格交叉點處作為彈丸落點,其中,400 m <x<1 400 m ,400 m <y<1 400 m被設定為關注區(qū)域。采用L型布站,在每條邊上逐步增加探測器數(shù)量,設每條邊探測器數(shù)量為 k。分別計算整個區(qū)域和關注區(qū)域中的落點,結果如圖4所示。
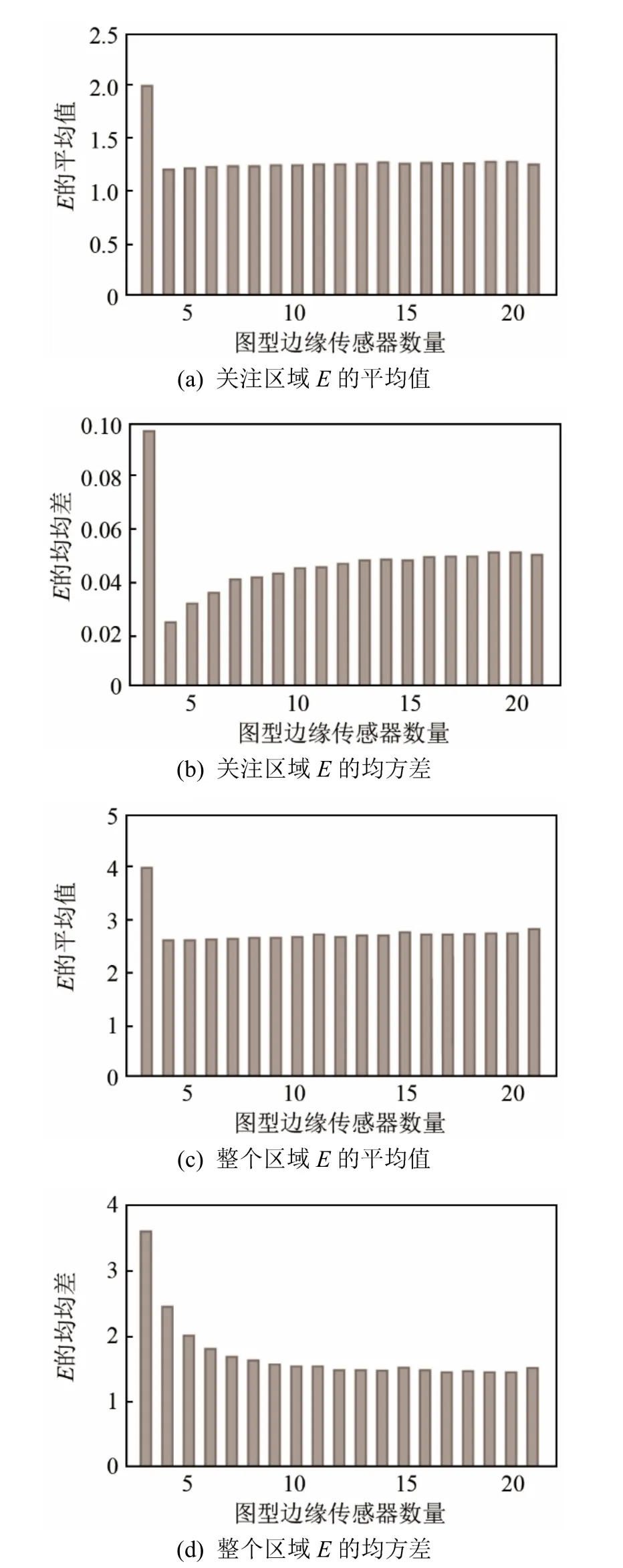
圖4 L型布站陣形受探測器數(shù)量的影響Fig.4 The influence of the number of sensors on the“L” type sensor layout pattern
不難看出,當k=2時,E的平均值和均方差均較大,即此時的結構最差。當k=3時,E的平均值和均方差明顯降低,隨著探測器數(shù)量的增加,圖形結構變化趨于平緩。對于整個區(qū)域,E的均方差逐漸減小,直到k=15時,趨于平緩;對于關注區(qū)域,E的均方差在k=2時最大,然后迅速減小,隨著探測器數(shù)量的增加,E的均方差逐漸增大,直到k=18時,趨于平緩。
采用口字型布站,用同樣的方式進行計算,得出的結果如圖5所示。
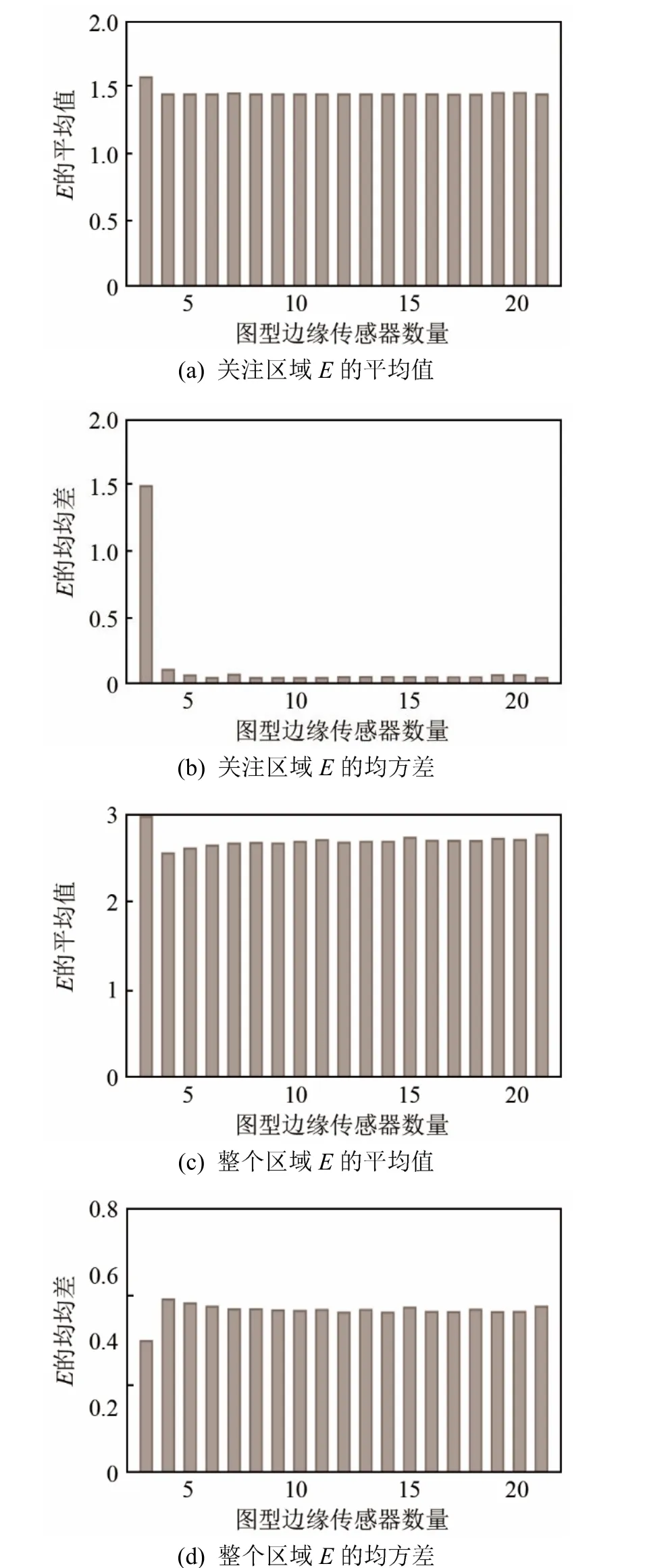
圖5 口字型布站陣形受探測器數(shù)量的影響Fig.5 The influence of the number of sensors on the“口”type sensor layout pattern
可以看出,對于整個區(qū)域,當k=2時,E的平均值最大,而均方差最小。當k=3時,E的平均值稍有下降,隨著探測器數(shù)量的增加,圖形結構變化趨于平緩;當k=3時,E的均方差相對于k=2時有所提高,隨著探測器數(shù)量的增加,E的均方差略有下降,直到k=8時,趨于平緩。對于關注區(qū)域,當k=2時,E的平均值和均方差最大,當k=3時,E的平均值略有降低,隨著探測器數(shù)量的增加,趨于平緩,而E的均方差在k=2時最大,當k=3時,E的均方差迅速降低,隨著探測器數(shù)量的增加,趨于平緩。
通過上述分析,可以總結出如下結論:
(1) 探測器的布站數(shù)量,需要根據試驗的具體情況決定。
(2) 不同的布站陣形,探測器數(shù)量對觀測結構的影響是不同的。
(3) 當L字型布站時,每條邊應布設至少3個探測器,當布設超過 10個以后,再增加探測器數(shù)量,對測試結果不再產生影響。
(4) 當口字型布站時,每條邊應布設至少3個探測器,當布設超過5個以后,再增加探測器數(shù)量,對測試結果不再產生影響。
3 試驗算例與分析
3.1 布設圖形對定位精度影響
為了進一步驗證本文方法的有效性,設計了一個模擬試驗的場景,采用爆竹代替彈丸產生聲源,探測器選型一致,可假設時延估計精度一致。試驗當天天氣晴朗,空氣濕度較低,無風,在一塊相對平坦的場地,分別以L型、U字型、||型、口字型、田字型五種方式布設探測器陣列,間隔為100 m,在每個陣列內部均勻放置 15個爆竹,在外部均勻放置 10個爆竹,用北斗定位設備精確測量其位置坐標,定位精度為2 cm。依次點燃爆竹,采集聲波數(shù)據,并采用1.1小節(jié)的計算方法對爆竹位置進行定位解算,將解算結果與北斗設備的測量結果進行比對,結果如表3所示。
表3中均方根誤差采用貝塞爾公式進行計算,其計算公式為
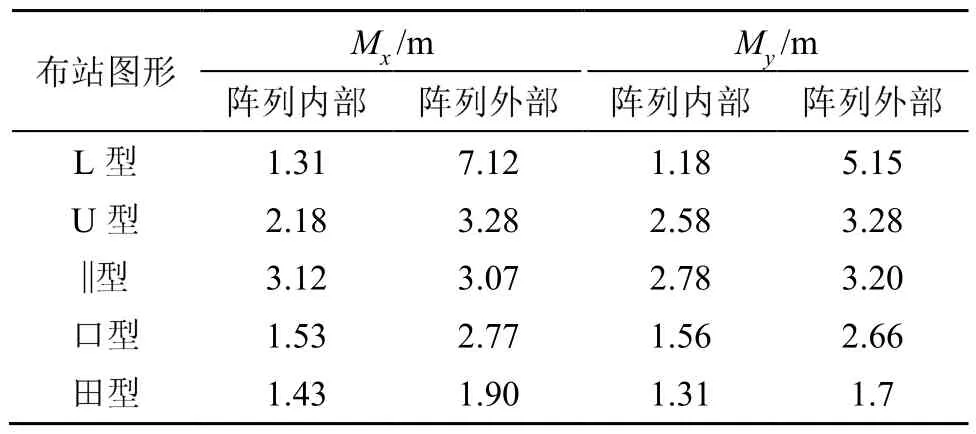
表3 布設圖形對定位精度影響Table 3 The effect of the sensor layout pattern on positioning accuracy

式中:Mx,My分別為x,y方向上的均方根誤差,Δx,Δy為解算結果與北斗測量結果在x,y方向上的坐標差,n為聲源個數(shù)。
從表3可以得出,當聲源位于陣列內部時(即位于關注區(qū)域內),L型的誤差較小,||型及U字型的誤差較大;當聲源位于陣列外部時,L型的誤差較大,其他四種方式相差較小。這與2.1小節(jié)的分析結果一致。
3.2 探測器數(shù)量對定位精度影響
文章選用L字型布站方式進行驗證,圖形的每條邊探測器數(shù)量k分別為2、3、5、8、10,試驗方法和步驟與3.1小節(jié)一致,結果如表4所示。
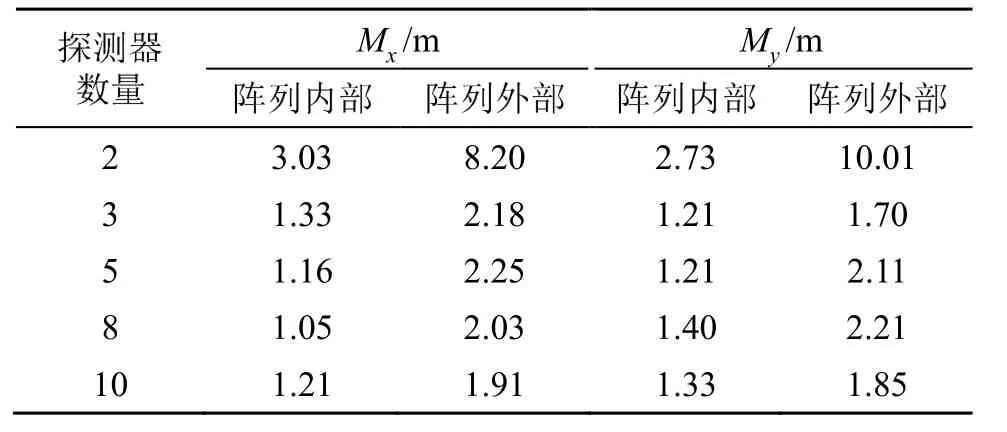
表4 探測器數(shù)量對落點坐標精度的影響Table 4 The effect of the number of sensors on positioning accuracy
從表4可以得出,當聲源位于陣列內部時(即位于關注區(qū)域內),k=2,誤差較大,隨著探測數(shù)量的增加,定位精度明顯提高;當聲源位于陣列外部時,k=2,誤差達到10 m,當k=3時,精度明顯提高,在基礎上進一步增加探測器數(shù)量,則精度無明顯提高,這與2.2小節(jié)的分析結果一致。
4 結 論
本文提出了一種度量布站陣形結構優(yōu)劣的方法。該方法基于觀測向量組空間幾何特性分析理論,從探測器組成的布站陣形和布設探測器的數(shù)量兩個方面來度量布站方案的優(yōu)劣,可為設備布站方案設計提供理論依據,能有效提高設備的測試精度和使用效率。

