視覺信息位姿估計在火箭起飛漂移量中的應用

高 燕，夏 霏

(太原衛星發射中心，山西 太原 030027)

0 引言

在火箭點火起飛至離開發射塔架前，火箭垂直向上飛行，火箭在該階段由于控制的延遲和超調等原因出現擺動，表現為橫向漂移，漂移量就是指火箭垂直起飛過程中相對基準彈道的偏移，主要用于評定火箭的飛行控制性能。目前火箭起飛漂移量主要依靠高速電視攝像機交匯測量實現，該方法對圖像判讀要求較高，并且測量精度偏低。

位姿估計是視覺測量方法中的基礎問題，常用在空間目標交匯對接、飛行器導航與目標定位等方面。李少飛[1]提出基于原始點云對物體進行6D位姿估計的深度學習方法，僅依靠三維點云信息對散亂場景中的物體進行位姿估計。蔣雪源等[2]提出采用動態遍歷與預聚類相結合的視覺定位方法，能夠有效提高位姿估計的精度。許允喜等[3]提出了擴展正交迭代算法，同時利用點和直線段的特征，定義誤差函數，迭代求解其最小值，使得位姿估計誤差更低、抗噪性更強、算法更穩定。洪洋等[4]利用矩形的幾何特性及空間點、線的共面特征，通過獲取一對正交消隱點，確立無窮遠點在像平面的投影關系，完成姿態估計。郭軍等[5]引入三維重構信息，克服了正交迭代算法的位姿模糊，提高了位姿估計的收斂速度和魯棒性。李鑫等[6]利用直接最小二乘法實現了高精度的相機位姿估計。凌寒羽等[7]在高精度快速位姿估計算法中，加入改進的自適應加權物方殘差目標迭代算法，提高計算精度和穩健性。席志紅等[8]提出將不確定性描述矩陣加入到位姿求解等式中，使得求解精度更高，穩定性更強。

多目位姿估計是當前采用較多的方法，其基本原理是利用多臺相機對目標進行拍攝，最終獲取目標坐標系和相機坐標系之間的位姿轉換關系，其求解過程稱為透視n點投影問題(Perspective-n-Point，PnP)。

結合火箭起飛漂移量應用實際，提出基于視覺信息的起飛漂移量測量計算方法，利用單幅圖像對測量設備進行準確標定，并使用正交迭代算法求解箭體的位置和姿態，試驗結果表明該方法有較高的測量精度。

1 視覺信息位姿估計原理

通常使用中心透視投影模型表示相機的成像過程,如圖1所示。該模型為一線性模型，假設物體表面的反射光或發射光都經過一個“針孔”點而投影在像平面上，此投影中心或針孔稱為光心，滿足物點、像點和光心三點共線，并據此建立中心投影的基本方程——共線方程[9]。

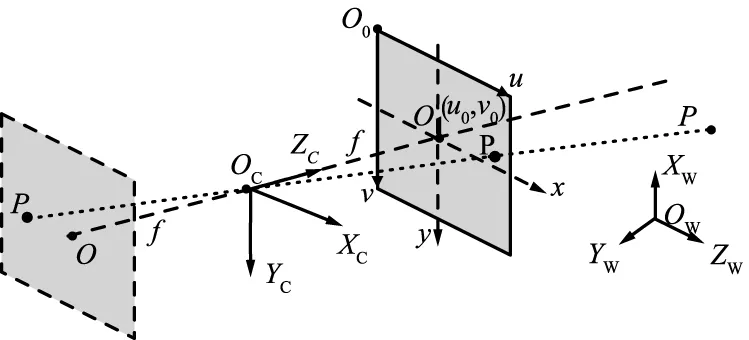
圖1 中心透視成像模型Fig.1 Central perspective imaging model

圖1中，Ow-XwYwZw為世界坐標系;Oc-XcYcZc為攝像機坐標系;Oc為光心。平面O0-uv和平面O1-xy均為成像平面，其中O0-uv以像素為單位建立坐標系，平面O1-xy以物理單位建立坐標系，原點O1為相機光軸與成像平面的交點，其在平面O0-uv的坐標為[u0,v0]，像素在2個方向的物理尺寸為[dx,dy]。

設像點P的像素坐標為[u,v]，圖像坐標為[x,y]，物點P在世界坐標系中的坐標為[Xw,Yw,Zw]，在攝像機坐標系中的坐標為[Xc,Yc,Zc]，則根據共線關系，存在：

(1)

式中，fx,fy為橫向和縱向等效焦距，表示實際光學焦距與像元的橫縱長度之比。

設世界坐標系到攝像機坐標系的坐標轉換矩陣和平移向量為{R ,t}，則：

(2)

結合上兩式，得到：

(3)

式中，K為內參矩陣，反映相機內部的固有特性，與等效焦距和主點相關。{R,t}為外參矩陣，與相機在世界坐標系中的位置和姿態相關，反映了相機的外部位姿。

在實際的成像系統中，物像之間理想的線性投影關系并不能實現，由于各種因素的影響，成像投影點與投影幾何中心存在偏差，稱之為光學畸變誤差，其存在會影響最終結果的正確性，因此需要建立像差模型對該誤差進行修正。相機成像偏差并非只受單一因素影響，是由多種類型畸變綜合作用的結果，一般包括徑向畸變、切向畸變和薄棱鏡畸變[10]。在忽略各種畸變的高階項后，理論像點和實際像點可表示為：

，

(4)

式中，k1，p1，p2，s1，s2為相差系數，已知相差系數可以對圖像進行有效修正，從而保證測量結果的正確性。由于相差系數只與相機本身的成像性質有關，所以相差系數可以認為是相機內部參數的一部分。

綜上所述，相機的成像過程如圖2所示，某點在世界坐標系中的坐標經過剛體坐標變換，得到該點在相機中的坐標，經過透視投影，得到理想圖像坐標，相差修正后得到真實圖像坐標，最后經過處理得到該點的像素坐標。簡單的說，已知物點P對應像點的像素坐標[u，v]，及相機的內參系數fx，fy，u0，v0，外參矩陣R，t，相差系數k1，p1，p2，s1，s2，可以求得該點在世界坐標系中的坐標。

圖2 相機成像過程示意圖Fig.2 Schematic diagram of camera imaging process

2 相機標定

由上一節可知，利用視覺信息進行物體的位姿估計，需要先知道相機的內外參數及相差系數，相機參數的獲取通過相機標定實現，其標定的準確程度將會直接影響最終測量精度。

鑒于三維坐標維度信息充足、測量方便和求解效率高的優點，采用三維標定參照物的方式進行標定測量。在測量空間中布置一系列非共面靶標，要盡可能充滿整個視場，在線性運算基礎上利用歸一化的求解方式進行多點迭代運算，通過單張圖像實現內外參數的求解。即利用已知靶標的圖像坐標及對應的世界坐標估計相機內外參數的初值，與鏡頭畸變參數一起進行非線性優化搜索，估計出所有參數的最優解[11]。

若引入投影矩陣：

(5)

則式(3)可以描述為關于像點的顯示表達：

(6)

可將方程組(6)寫成矩陣形式：

(7)

式中，m中未知量的個數是11，已知標定點的二維像素坐標和三維世界坐標，要求解式(7)，那么標定點的數量只要保證N≥6即可。由于方程的個數大于未知量的個數，因此該方程組為超定方程組，利用最小二乘法進行求解，其結果為：

m=(ATA)-1ATU。

(8)

上述過程中沒有考慮圖像畸變和噪聲的影響，只能獲得粗略的內外參數結果。為了提高精度，以式(8)的計算結果為初值，采用LM(Levenberg-Marquardt)算法進行迭代優化，構造目標函數為：

(9)

3 多相機正交迭代算法

在計算過程中需要建立火箭的箭體坐標系Om-XmYmZm來反映箭體上所有點的信息，原點Om位于箭體尾部中心，Ym軸與箭體縱軸重合指向火箭頭部，Xm軸在箭體縱對稱面內，垂直于Ym軸，在火箭平飛時指向上方，Zm軸與Xm、Ym構成右手坐標系。火箭在飛行過程中，其上各點坐標在箭體坐標系中的位置不變，可以用來描述空間點對箭體的位置關系和火箭姿態。通過箭體坐標系到世界坐標系的轉換矩陣和平移向量{Rmw,tmw}，可以將箭體上各點在箭體坐標系下的位置轉換為世界坐標系下的位置：

(10)

將式(10)帶入式(3)可以得到：

(11)

{Rmw,tmw}反映了火箭在世界坐標系中的位姿。由式(11)可知，在已知箭體上多個目標點的箭體坐標(Xm ,Ym,Zm)、相機拍攝的對應目標點的圖像坐標(u,v)及相機的內外參數K,Rwc,twc的條件下，可以對{Rmw,tmw}進行求解。

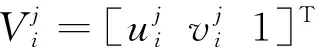
控制點pi在多攝像機系統坐標系的坐標qi=Rpi+t；

物方殘差矢量在多攝像機系統坐標系下表示為：

(12)

多攝像機系統的位姿估計問題可以轉化為最小化下式的物方殘差平方和：

(13)

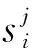
步驟1：對于第k次迭代，給定R的值，則t存在最優解：

tk=t(Rk)=

(14)

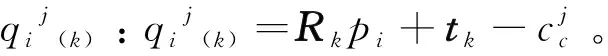
步驟3：根據誤差函數則有：

(15)

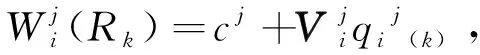
(16)

可以得到：Rk+1=argmin(R)tr(RTM(Rk))。

對M(Rk)進行奇異值分解SVD，記為M(Rk)=UDTT，其中D=diag(σ1,σ2,...,σn)，得到式(16)問題的最優解為：

Rk+1=UVT。

(17)

步驟4：判斷迭代矩陣的收斂性，設定一個閾值，當目標函數小于這個閾值，或者目標函數的相對變化量小到一定程度，或者達到了預設的迭代次數上限，迭代停止，輸出位姿參數R和t，否則返回步驟1重新計算。

4 測量結果計算與分析

4.1 仿真實驗

仿真實驗在Matlab環境下運行，依據透視投影原理將物體投影到攝像機平面，由于攝像機誤差和特征點提取誤差的存在，為模擬真實性，在圖像特征點中加入噪聲。

本實驗中，攝像機內部參數為：等效焦距為(2 200，2 200)，主點為(1 024 pixel，1 024 pixel)，像面大小為(2 048 pixel×2 048 pixel)，取3個攝像機組成多攝像機系統。定義目標物尺寸為[-10,10]×[-10,10]×[-10,10]的立方體，在其表面均勻分布6個點作為標志點，3臺相機獲取的總標識點數為12個，3臺相機布站在與參考點坐標系原點的距離為100，且光軸指向原點的位置，目標的標志點投影到歸一化圖像平面產生圖像點，在圖像點中加入均值為零，標準方差為1 pixel的高斯噪聲，隨機仿真500次，統計誤差均值。旋轉矩陣的誤差計算公式為ER=arccos((tr(RTRg)-1)/2)，平移量的誤差計算公式為Et=‖t-tg‖/‖tg‖·100。

算法隨著噪聲、點數、攝像機個數增加的位姿估計誤差如圖4所示。從圖4中可以看出，隨著加入的噪聲級別、點數和相機個數的不斷增加，旋轉矩陣和平移量的誤差變化逐漸減小，可以看出算法有效且精度較高。

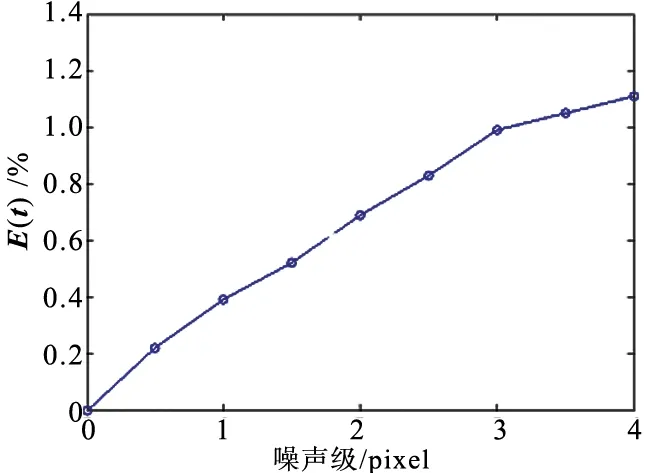
(a) 旋轉矩陣誤差隨噪聲級變化圖

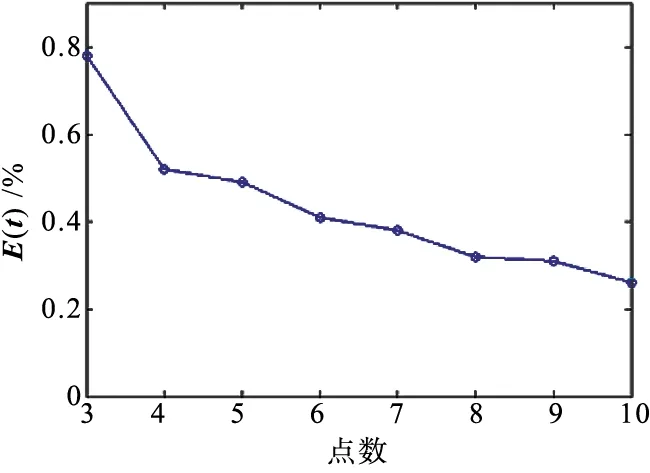
(b) 旋轉矩陣誤差隨點數變化圖

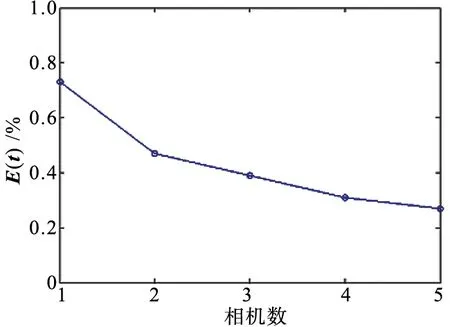
(c) 旋轉矩陣誤差隨相機數變化圖

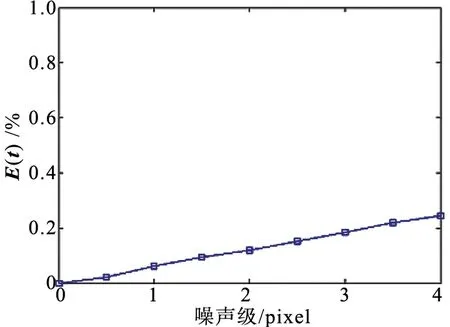
(d) 平移量誤差隨噪聲級變化圖

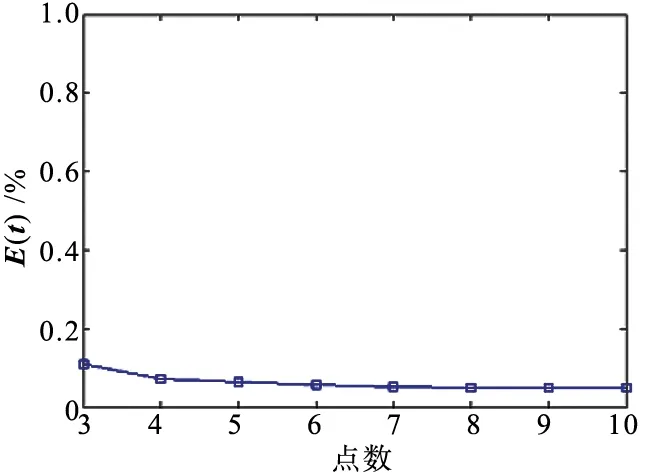
(e) 平移量誤差隨點數變化圖

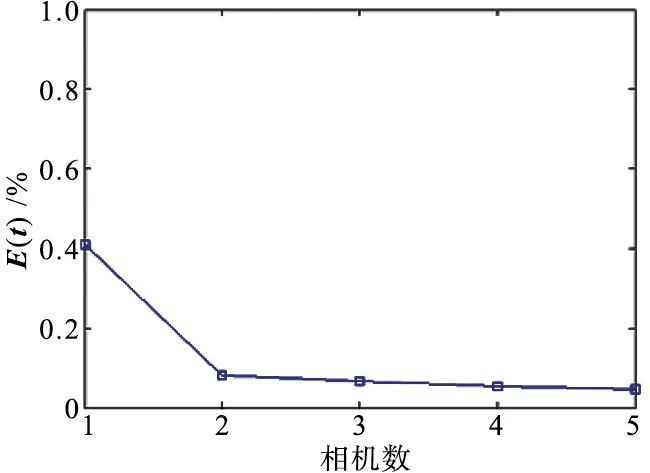
(f) 平移量誤差隨相機數變化圖

4.2 真實實驗

將上述方法應用在實際情況中，其解算過程為：① 對高速電視測量系統進行標定，方法為在設備視場內選取已知點作為標志點，測量標志點的大地坐標，每個視場內至少需要6個標志點，且標志點最好均勻分布在整個視場。對拍攝的單幅圖像中的標志點進行判讀，結合測站和發射點的大地坐標，對設備內外參數進行精確標校，得到設備相機的等效焦距，光心在測量坐標系中的位置，相機坐標系到發射坐標系轉換矩陣等參數；② 將發射坐標系作為這個多攝像機系統的攝像坐標系，以火箭中心為原點建立箭體坐標系，依據火箭外形尺寸計算火箭上所有測量點在箭體坐標系中的坐標；③ 對各相機每個圖像中的測量點進行判讀，并用判讀結果進行逐點多目正交迭代解算，獲得各測量時刻箭體坐標系到攝像坐標系的轉換矩陣，從而解算出各測量點的漂移量參數。

將起飛前火箭中心的漂移量位置參數與實測值進行比對，統計其在各方向上的總誤差均在厘米級，在一定程度上可以反映火箭起飛漂移量的測量精度。

5 結束語

利用攝像機視覺測量的結果，將單幅圖像中多個已知空間位置的特征點進行標定，從而獲得多臺攝像機的內外參數，在此基礎上，對多攝像機拍攝的全部圖像序列統一表達，再把圖像上特征點的物方殘差作為目標函數，最后使用多目正交迭代算法求解各時刻箭體的位置和姿態，得到箭體各位置的漂移量。仿真和實際測量結果都表明，該方法是有效、精確的。但在解算過程中發現，由于火箭起飛過程中存在運動模糊現象，以及火箭起飛時會引起相機抖動，都給解算結果帶來誤差。基于此，下一步可以進一步分析誤差模型，尋求適應性更強的解法。