基于單元過濾的自支撐結構拓撲優化方法

王雷,閆素娜,趙強強,洪軍

(1.西安交通大學機械工程學院,710049,西安;2.西安交通大學現代設計及轉子軸承系統教育部 重點實驗室,710049,西安;3.中國電子科技集團公司第二十七研究所,450047,鄭州)

拓撲優化受到傳統制造技術的限制,實際工程應用的拓撲優化結構仍然有一定的局限性,沒有充分發揮拓撲優化的優勢。近年來,增材制造技術得到了快速發展,與傳統制造技術相比,它具有能夠實現高效率、低成本、制造復雜結構的突出優勢[1],為拓撲優化結構的制備提供了強大的工具,極大地拓寬了結構設計的空間。因此,將拓撲優化與增材制造結合,研究面向增材制造的創新設計方法具有廣闊前景[2]。然而,增材制造技術存在一些工藝約束,制約著優化結構的制備,例如懸垂特征,打印時需要在其下方添加支撐防止坍塌,打印完成后再通過人工去除,不僅浪費打印材料和打印時間,而且去除支撐會對零件性能和表面質量造成損壞[3]。

為了減少使用支撐,一些學者從工藝參數方向入手,利用優化算法尋找能夠使支撐體積最小的最佳成型方向。其中,Das等提出了一種利用多目標優化方法,在滿足零件GD&T標準的同時,尋找能夠使支撐體積最小的成型方向[4];Morgan等提出了一種利用優化算法尋找使支撐體積最小的成型方向的方法[5];Strano等提出了一種兩步優化設計結構的方法,第一步尋找結構最優打印方向,第二步基于此方向優化設計多孔支撐結構,使支撐體積最小[6]。上述通過優化算法尋找最佳成型方向的方法只能使支撐體積達到最小,不能完全避免使用支撐。

另一些學者從結構設計方向入手,研究面向增材制造的自支撐結構設計方法。其中,Laery等提出了一種基于熔融沉積成型(FDM)工藝的自支撐條件,通過修改結構構型,使結構打印時無需支撐[7];Li等提出了一種面向激光選區熔化(SLM)工藝的零件輕量化/無支撐優化設計方法,第一步獲得拓撲優化結構,第二步使用自支撐結構元素修改結構構型[8];桂馨提出了一種基于固體各向同性材料懲罰模型(SIMP)法和能量均勻化法的自支撐結構多尺度拓撲優化,在宏觀結構優化階段,利用SIMP法獲取自由分布的宏觀材料空間,從而劃分微結構類型區域,在微結構設計階段,進行自支撐微結構設計,最終獲得自支撐結構[9]。上述通過修改結構構型來獲得自支撐結構的方法會造成結構體積的增加,而且添加的材料會影響結構性能。

Garaigordobil等提出了一種使用輪廓檢測算法提取結構邊界,通過顯示不等式約束條件控制邊界法向量的傾斜角,從而獲得自支撐結構的方法[10];Qian提出了一種基于密度梯度信息確定結構邊界,通過顯示約束條件控制邊界傾斜角的方法[11];Zhang等提出了一種利用局部單元密度確定邊界法向量的方法,通過控制法向量傾斜角來控制邊界傾斜角和懸吊特征尺寸[12]。上述通過邊界法向量控制邊界傾斜角的方法需要通過密度梯度信息提取結構邊界法向量信息,增加了優化時間。Zhao等提出了一種通過卷積算子判斷單元的支撐性,通過顯示約束條件控制非自支撐單元數量,最終獲得自支撐結構的方法[13],此方法需要在傳統拓撲優化的基礎上確定成型方向,再進行自支撐結構優化設計;Kuo等提出了一種使用連續邏輯聚合函數評估單元支撐狀態的方法,以顯示約束形式加入到結構拓撲優化方法中,優化設計自支撐結構[14];鄒君等提出了一種使用顯示約束函數表征結構自支撐約束違反程度,并控制此函數值的方法優化設計自支撐結構[15]。上述通過顯示約束條件控制非自支撐單元的數量的方法會增加優化問題求解難度。

Gaynor等提出了一種通過映射單元設計變量的方法實現結構最小特征尺寸和最大懸垂角度的控制[16],但其扇形支撐區域包含太多單元,計算復雜。Langelaar提出了一種過濾方法,模擬增材制造成型過程逐層過濾單元進行自支撐結構的優化設計,并將結構優化、支撐結構布局和成型方向3個目標結合,尋求最優結構設計和成型方向[17-18];Pellens等提出了4種不同形式的過濾器,以不同順序組合進行過濾,將特征尺寸和懸垂角度約束合并到結構拓撲優化問題中進行結構優化設計[19];Wang等提出了一種基于分層過濾策略的SIMP改進方法和一種基于懸垂靈敏度分析的雙向漸進結構拓撲優化(BESO)改進方法以減少優化設計中懸垂結構的產生[20];杜義賢等通過建立每個單元的可打印密度與相應支撐區域內單元的可打印密度之間的關系來過濾掉不符合約束條件的結構,優化設計自支撐結構[21];Zou等提出了一種基于max/min函數識別非自支撐單元,通過不等式約束控制非自支撐單元數量,得到自支撐結構的方法[22]。上述過濾方法中采用近似max/min函數通過判斷上下相鄰單元的密度關系,確定單元的自支撐性,此判斷條件不符合實際逐層堆積成型原理,會出現自下向上密度逐漸增加的現象。

Luo等提出了一種自支撐封閉空腔結構拓撲優化方法,其采用非線性虛擬溫度法(N-VTM)識別封閉空腔,通過多重過濾識別懸垂面,基于對數函數的約束控制封閉空腔的最小懸垂角[23];Guo等提出了一種基于移動可變形組件的自支撐結構設計方法,通過控制組件的傾斜角度保證組件自支撐,最終獲得自支撐結構[24];Emiel等將設計域分層,以設計域內每個點材料到達時間為判斷依據判斷支撐性,優化設計自支撐結構[25];王亞光等提出了一種基于參數化水平集法的懸垂約束處理方法[26];韓永生等提出了一種基于BESO法的無需支撐(自支撐)拓撲優化方法[27]。

本文模擬增材制造逐層堆積材料的成型過程,提出一種基于Heaviside函數的自支撐單元過濾法則,并基于此構建面向增材制造的自支撐結構拓撲優化方法,旨在解決傳統拓撲優化結構在增材制造過程中需要使用支撐的問題。最終,通過數值案例驗證本文所提方法的有效性,結果表明本文所提方法能夠在4個方向上對二維結構進行優化設計,實現打印過程自支撐,并且在保證結構剛度的前提下,節省打印材料和打印時間。

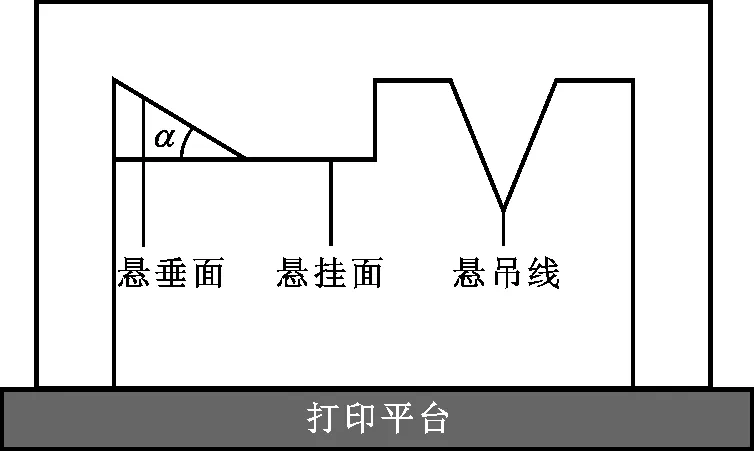
圖1 增材制造懸垂特征模型示意圖Fig.1 Schematic diagram of overhang features in additive manufacturing

1 自支撐單元過濾法則

1.1 增材制造懸垂特征

圖1給出了增材制造懸垂特征模型示意圖,懸垂特征模型主要包括傾斜角α小于自支撐臨界角的懸垂面、懸吊面和懸吊線。

為了避免使用支撐,對于懸吊面和懸吊線特征,設計階段可以在其下方添加特征連接至打印平臺;對于懸垂面特征,Thomas研究了SLM工藝自支撐臨界角為45°[28],則可以在設計階段使傾斜角α大于45°,從而無需添加支撐。

1.2 自支撐單元過濾法則

圖2給出了懸垂面特征模型及其有限元模型,傾斜角為45°,采用長寬比為1∶1的四節點矩形單元離散此模型,構建如圖2b所示懸垂面特征有限元模型。

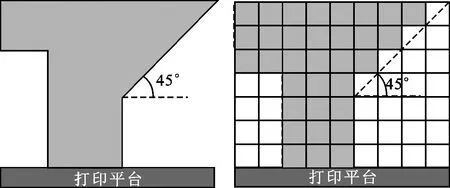
(a)懸垂面特征模型 (b)懸垂面特征有限元模型圖2 懸垂面特征模型及其有限元模型 Fig.2 Overhang model and its finite element model in additive manufacturing

取單個單元作為研究對象,圖3給出了自支撐單元過濾法則示意圖,成型方向為豎直向上,目標單元xij與其支撐單元集3個單元形成最小傾斜角為45°的傾斜面,其中i和j分別表示單元水平和垂直方向的位置。

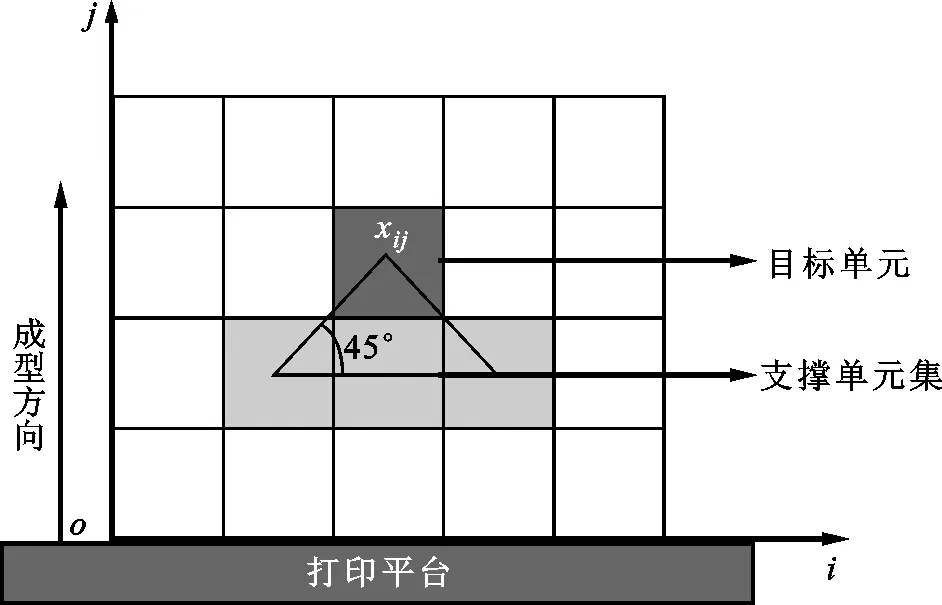
圖3 自支撐單元過濾法則示意圖Fig.3 Schematic diagram of filtering rule of self-supporting element

目標單元是否自支撐與支撐單元集中3個單元密度有關,若支撐單元集中至少有一個單元密度大于0,則目標單元為自支撐單元。基于上述條件可得自支撐單元判斷法則為:若支撐單元集中單元平均密度大于0,則目標單元為自支撐單元,反之目標單元為非自支撐單元。對于設計域全局單元,將逐層判斷是否自支撐。

1.3 自支撐過濾特殊單元

設計域中存在一些特殊單元在優化算法中要特殊處理,包括邊界單元和底層單元,自支撐過濾特殊單元如圖4所示。

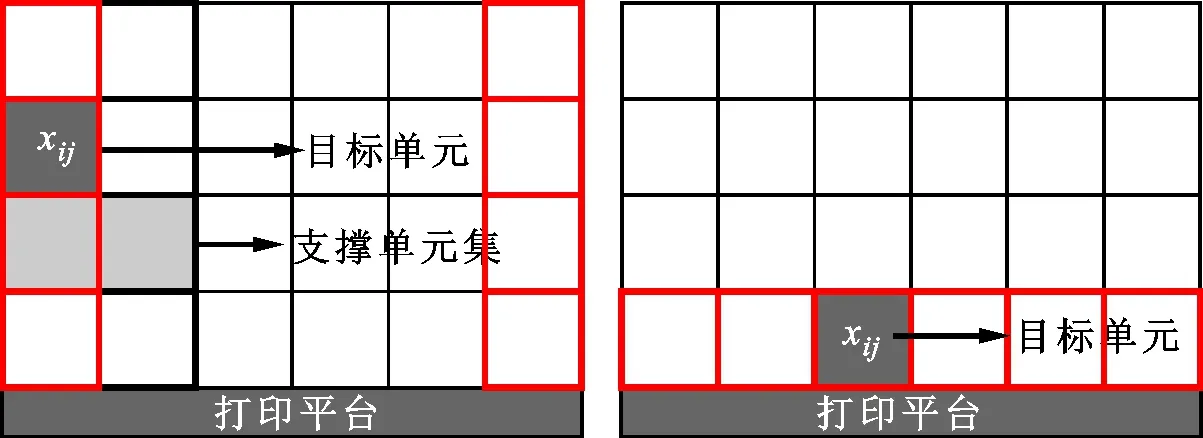
(a)邊界單元 (b)底層單元圖4 自支撐過濾特殊單元Fig.4 Special element of self-supporting filtering

邊界單元是指處于設計域兩側邊界的單元,如圖4a所示,它的特殊性在于支撐單元集中只包含2個單元。底層單元是指處于設計域底部的單元,如圖4b所示,與成型方向有關,它的特殊性在于直接與打印平臺連接,無論如何都是自支撐單元。

2 自支撐結構拓撲優化模型

2.1 自支撐單元過濾

采用自支撐單元過濾的方法判斷單元是否自支撐,保留自支撐單元,刪除非自支撐單元,自支撐單元過濾表達式如下

(1)

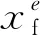
(2)

其中β為近似參數,T為閾值,Me為單元e支撐單元集中的單元平均自支撐密度,表達式如下

(3)

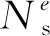
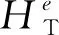
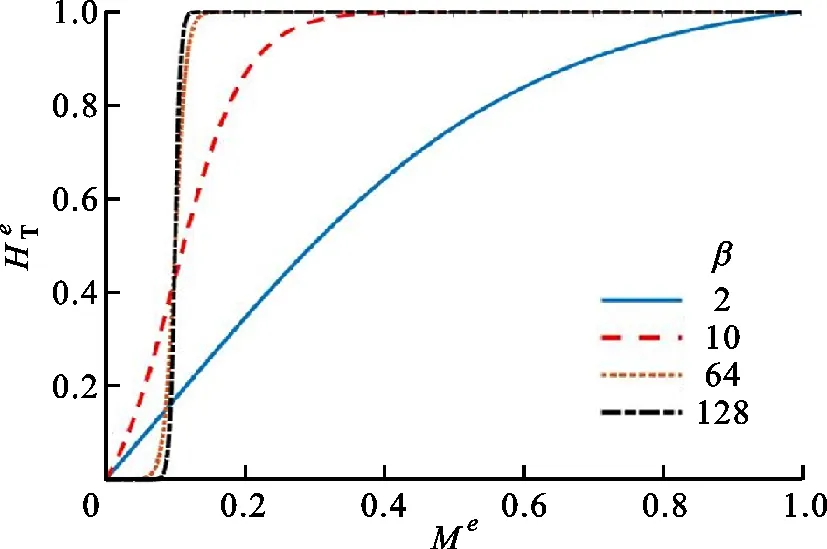
圖5 Heaviside閾值函數曲線Fig.5 Curve of Heaviside threshold function

2.2 單元密度過濾

棋盤格式解是指結構中出現實體單元與空白單元交替的現象,形成一種棋盤狀的構型,棋盤格式解如圖6所示,此結構在實際工程中無法應用。

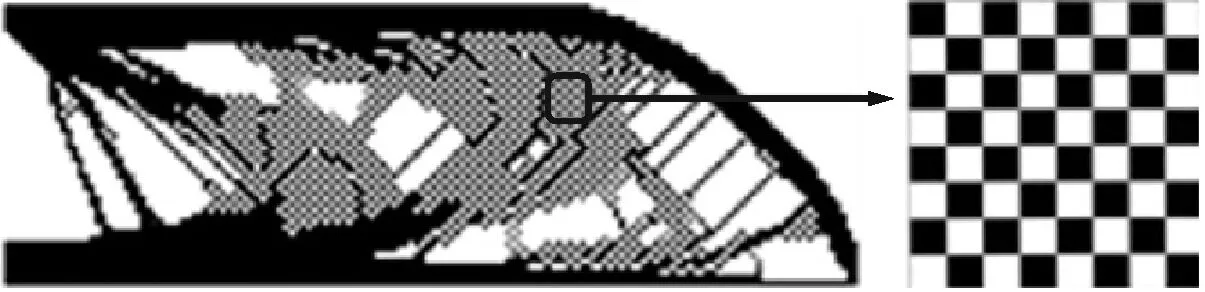
圖6 棋盤格式解Fig.6 Checkerboard solution

為了消除棋盤格式解現象,本文采用單元密度過濾法,其核心思想是利用過濾后的單元密度替代單元實際密度[29],單元物理密度表達式如下

(4)

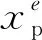
Ne={i|‖Xi-Xe‖≤rmin}

(5)

其中Xi為單元i的坐標,Xe為單元e的坐標,rmin為過濾半徑。

Hei表達式如下

Hei=max(0,rmin-Δ(e,i))

(6)

式中:Δ(e,i)為單元i和e中心距。密度過濾區域如圖7所示,是以目標單元e為圓心、過濾半徑rmin為半徑形成的圓形區域。

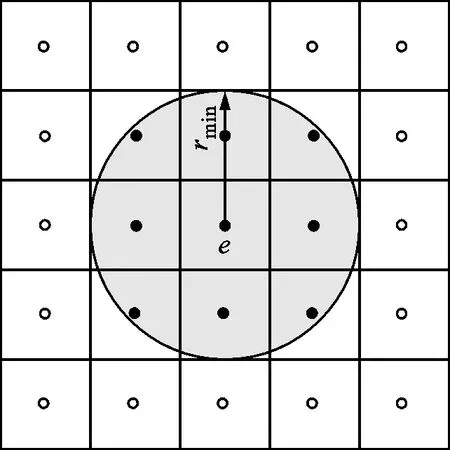
圖7 密度過濾區域Fig.7 Density filtering area

2.3 自支撐結構拓撲優化模型

基于SIMP變密度法,以最小化柔度(最大化剛度)為目標函數,以結構體積分數為約束條件,構建自支撐結構拓撲優化模型,數學模型如下

(7)

式中:c(x)為結構柔度;v為約束條件;x為單元設計變量;V(x)為結構體積;V0為設計域總體積;f為結構體積分數。

3 基于MMA的拓撲優化模型求解

本文所提的自支撐結構拓撲優化模型采用MMA法求解[30],更新單元設計變量x。

3.1 有限元分析

采用長寬比為1∶1的四節點矩形單元離散設計域,初始單元剛度矩陣為k0,基于SIMP模型計算單元e的單元剛度矩陣ke,表達式如下

(8)

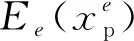
SIMP模型單元密度與彈性模量之間的關系可表示為

(9)

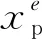
懲罰因子P是為了懲罰灰色單元密度,使其趨向0或1[31]。圖8給出了SIMP模型指數函數曲線,不同曲線代表不同P值,P值越大函數值越趨近于0或1。

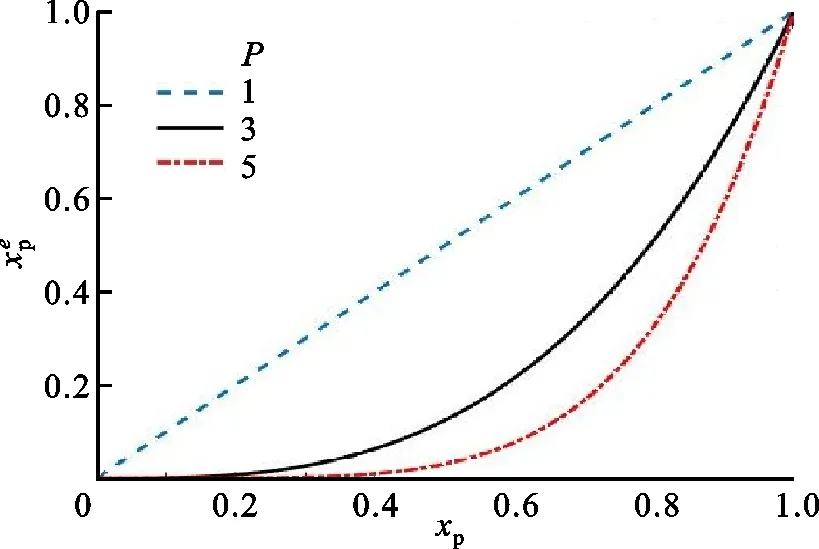
圖8 SIMP模型指數函數曲線Fig.8 Exponential function curve of SIMP model

通過組裝單元剛度矩陣求得整體剛度矩陣K,建立剛度方程求解整體位移矩陣U,剛度方程表達式如下

KU=F

(10)

式中:K為整體剛度矩陣;U為整體位移矩陣;F為已知載荷矩陣。

最終,通過U和K計算目標函數,結構柔度表達式如下

(11)

式中:n為離散化設計域單元的數量;ue為單元位移矩陣。

3.2 靈敏度分析

MMA求解需要分析目標函數和約束條件對設計變量的靈敏度,靈敏度信息決定設計變量的更新。其中,目標函數對設計變量的靈敏度表達式如下

(12)

式中:c為目標函數。

約束條件對設計變量的靈敏度表達式如下

(13)

式中:xf為單元自支撐密度。

3.3 自支撐結構拓撲優化流程

本文首先采用自支撐單元過濾,從更新的單元中過濾得到自支撐單元,保證設計域內只留下自支撐單元,再采用密度過濾消除棋盤格式現象,并且可以通過密度過濾避免結構中出現細小特征。然而,對于相反的過濾順序,通過試驗可知同樣可以得到最優的自支撐結構,但是優化結構中會出現細小特征,優化結構中的細小特征如圖9所示。

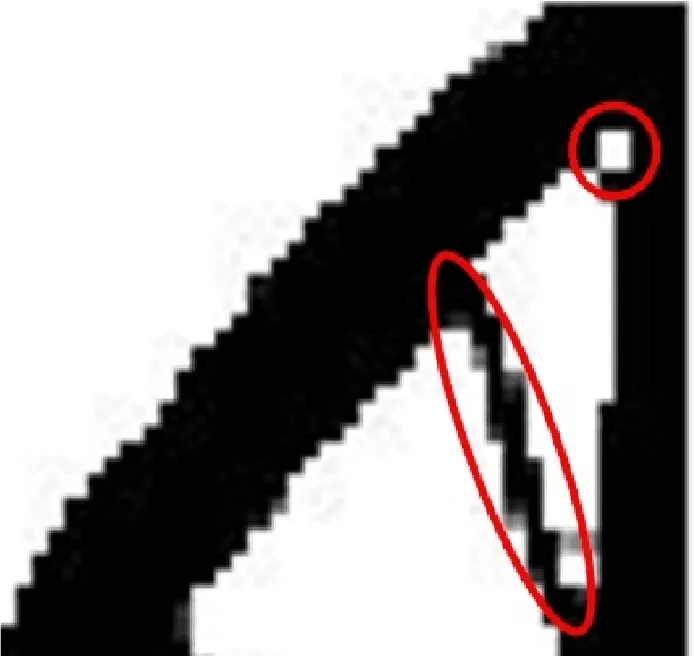
圖9 優化結構中的細小特征Fig.9 Small features in optimal structures

圖10給出了自支撐結構拓撲優化流程圖,具體步驟如下:

(1)前處理,定義結構幾何模型,添加邊界條件,施加載荷,設置優化參數;

(2)采用四節點矩形單元離散設計域;

(3)初始化單元設計變量x;

(4)自支撐單元過濾,單元密度由單元設計變量x轉換到單元自支撐密度xf;

(5)密度過濾,單元密度由單元自支撐密度xf轉換到單元物理密度xp;

(6)有限元分析,基于單元物理密度xp和初始單元剛度矩陣k0計算整體剛度矩陣K,求解整體位移矩陣U,計算目標函數和約束條件;

(7)靈敏度分析;

(8)采用MMA法求解優化模型,更新單元設計變量x;

(9)根據收斂條件判斷結果,如果不收斂則從步驟4繼續循環,直至收斂;如果收斂則輸出優化結果,并結束計算。

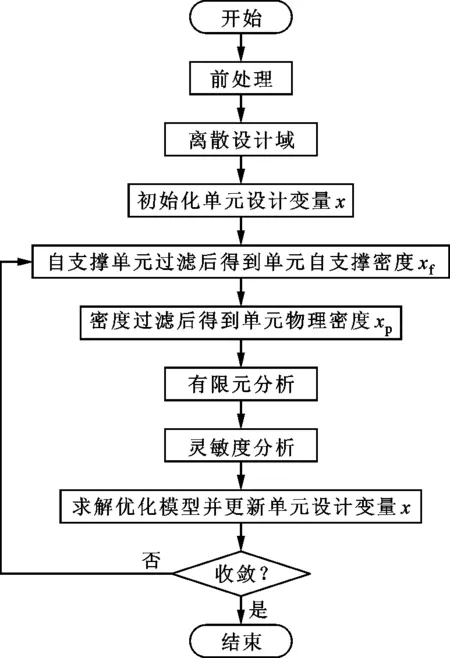
圖10 自支撐結構拓撲優化流程圖 Fig.10 Flow chart of self-supporting structures topology optimization

4 自支撐結構拓撲優化

應用本文所提的自支撐結構拓撲優化方法解決MBB梁拓撲優化問題。圖11給出了MBB梁對稱設計域,長寬比為3∶1,設計域左側添加滾動支撐,右下角添加滾動支撐,左上角施加沿-Y方向的單位集中載荷F。將設計域離散為180×60個單元,并初始化單元設計變量x為0.5。

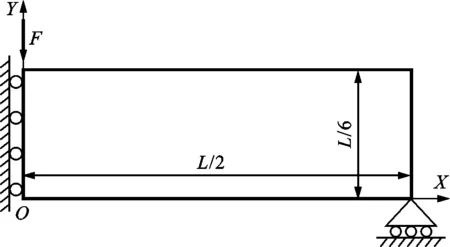
圖11 MBB梁對稱設計域Fig.11 Symmetric design domain of MBB beam

4.1 優化參數確定

在本文所提出的自支撐結構拓撲優化方法中,懲罰因子P決定著對灰色單元密度的懲罰程度,P值越大,單元密度越趨近0或1,但是會導致函數非線性程度增加;閾值T決定單元自支撐條件,T值越大,要求支撐集單元密度越大,單元自支撐條件越嚴苛。因此為了確定一組合適的P值和T值,本文以Y方向的MBB梁優化設計為例,選擇不同的參數P和T進行優化結果對比,最終根據優化結構的迭代步數和性能確定優化參數。

不同參數P和T優化結果對比如表1所示,可知懲罰因子P和閾值T對自支撐結構優化有重要的影響。T對結構優化的影響從T為0.1～0.4可知,迭代步數增大,結構柔度增大,特別在T為0.4時出現優化失敗的結果,所以T越大,會導致結構性能下降,迭代收斂難度增加,甚至出現優化失敗;P對結構優化的影響從P為2～5可知,結構中灰色單元明顯減少,結構邊界逐漸清晰,但是迭代步數增大,所以P越大,結果中灰色單元越少,但是會導致迭代收斂難度增加。

綜合分析,本文旨在保證結構中不存在大量灰色單元的前提下,使迭代步數減小,結構性能增加,得到最優的自支撐結構。從表1可知,在參數P為3、T為0.1的組合下,得到的結構柔度最小,迭代步數最小,并且沒有大量灰色單元存在。所以本文選擇P為3、T為0.1作為算例的優化參數組合,最終MBB梁拓撲優化參數取值如表2所示。

本數值案例由Matlab R2020b(64位)、Windows 10、Intel(R)Core(TM)i5-8400cpu@2.8GHz CPU、8GB RAM實現。

4.2 MBB梁拓撲優化設計

分別應用傳統拓撲優化方法和本文所提的面向增材制造的自支撐結構拓撲優化方法優化設計MBB梁。圖12給出了傳統拓撲優化MBB梁,迭代步數為565,柔度為194.8。

利用Autodesk Inventor Professional 2020提取優化結果數據,建立MBB梁三維模型,厚度設置為5 mm。利用Autodesk公司開發的3D打印輔助分析軟件Autodesk Netfabb Ultimate 2020沿Y、-Y、X、-X4個方向進行成型仿真分析,成型仿真分析參數如表3所示。

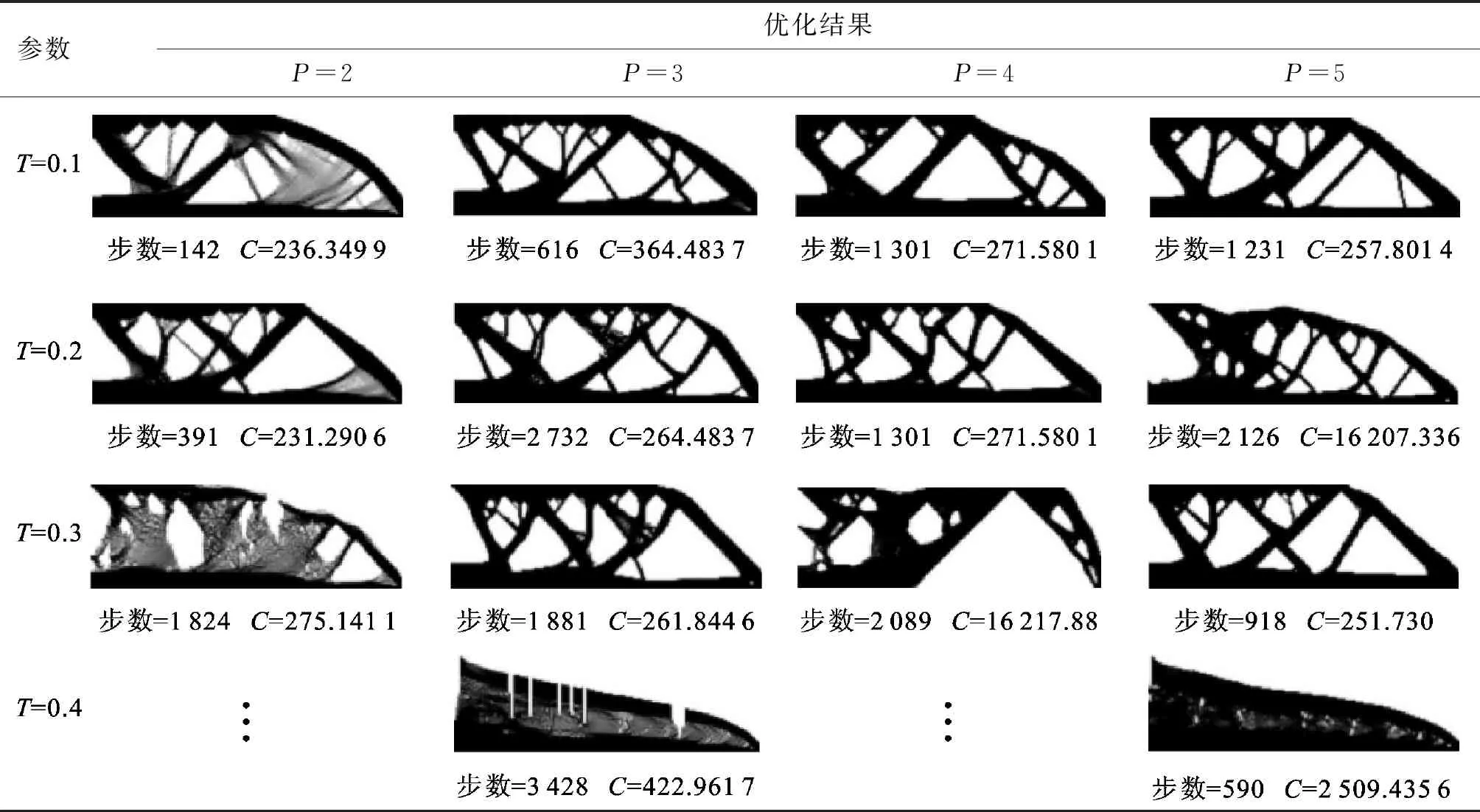
表1 不同參數P和T優化結果對比

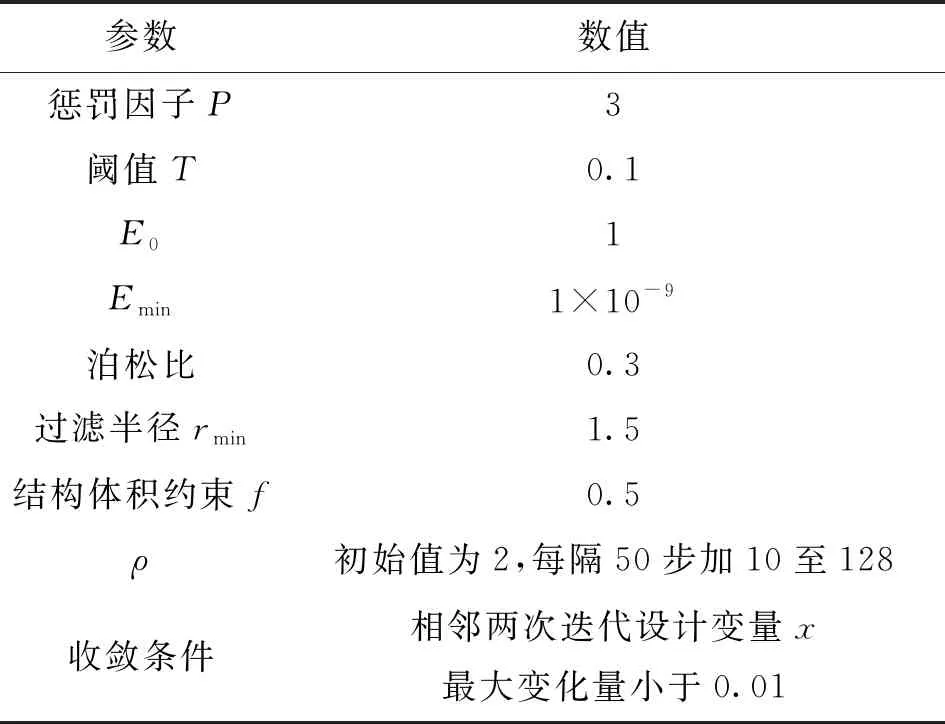
表2 MBB梁拓撲優化參數

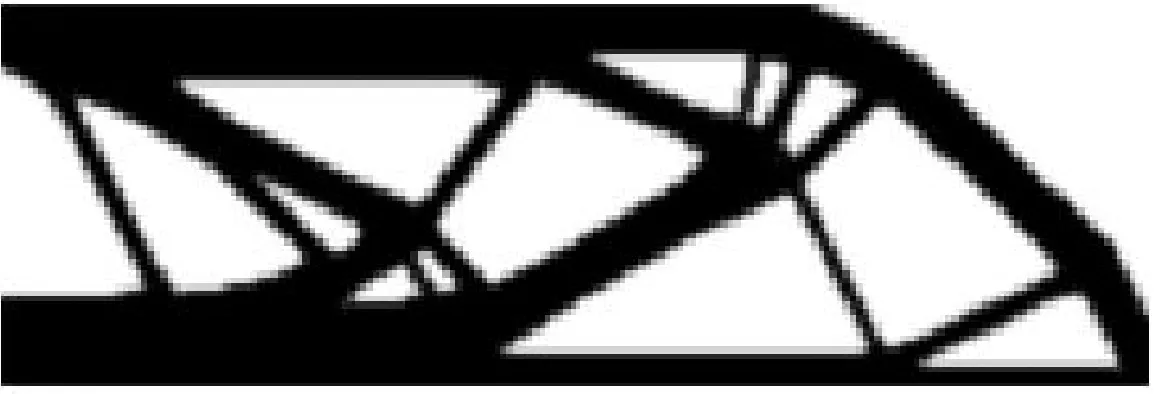
圖12 傳統拓撲優化MBB梁Fig.12 MBB beams with traditional topology optimization

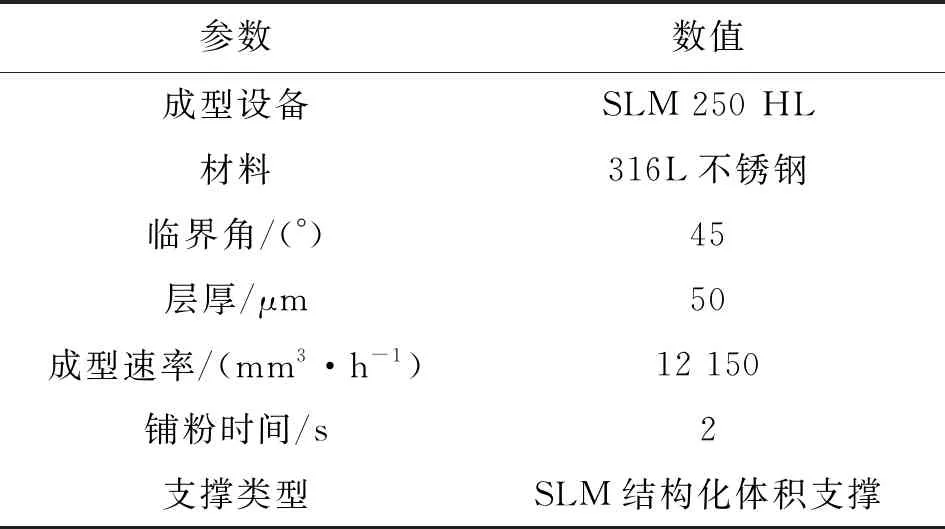
表3 成型仿真分析參數

圖13給出了傳統拓撲優化MBB梁分析結果,藍色部分為支撐。表4給出了傳統拓撲優化MBB梁成型數據統計。

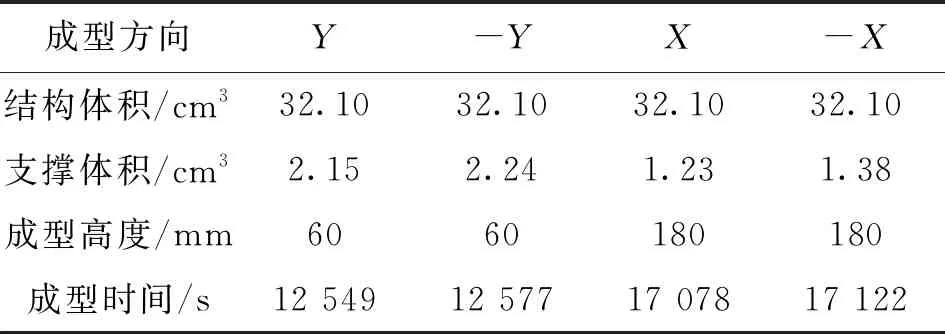
表4 傳統拓撲優化MBB梁成型數據統計

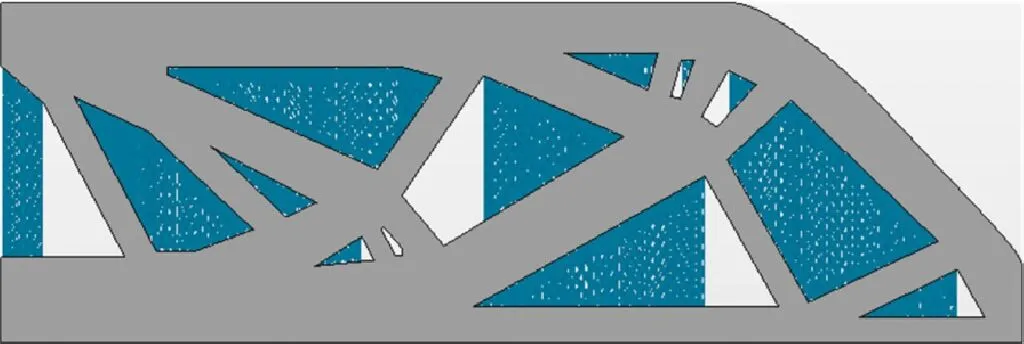
(a)Y方向分析結果

(b)-Y方向分析結果

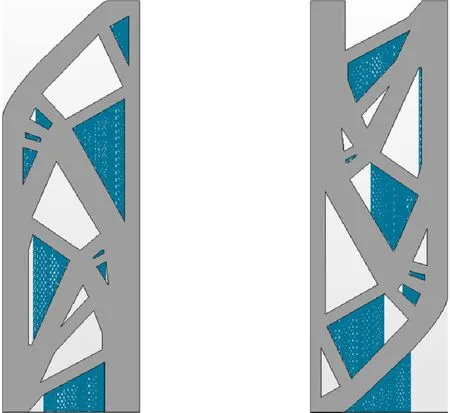
(c)X方向分析結果 (d)-X方向分析結果圖13 傳統拓撲優化MBB梁分析結果Fig.13 Analysis results of MBB beam with traditional topology optimization

圖14～17給出了Y、-Y、X、-X4個方向優化自支撐MBB梁及分析結果。圖14a給出了最終的優化結果,迭代步數為616,柔度為233.6;圖14b～17b給出了分析結果,無需支撐結構。

(a)Y方向優化結果

(b)Y方向分析結果圖14 Y方向優化自支撐MBB梁及分析結果 Fig.14 Optimized self-supporting MBB beam in Y direction and analysis results

圖15a給出了最終的優化結果,此結果出現振蕩。

(a)-Y方向優化結果

(b)-Y方向分析結果圖15 -Y方向優化自支撐MBB梁及分析結果 Fig.15 Optimized self-supporting MBB beam in -Y direction and analysis results

圖16a給出了最終的優化結果,迭代步數為1 297,柔度為194.4。

(a)X方向優化結果 (b)X方向分析結果圖16 X方向優化自支撐MBB梁及分析結果 Fig.16 Optimized self-supporting MBB beam in X direction and analysis results

圖17a給出了最終的優化結果,迭代步數為1 487,柔度為194.5。表5給出了自支撐MBB梁成型數據統計。

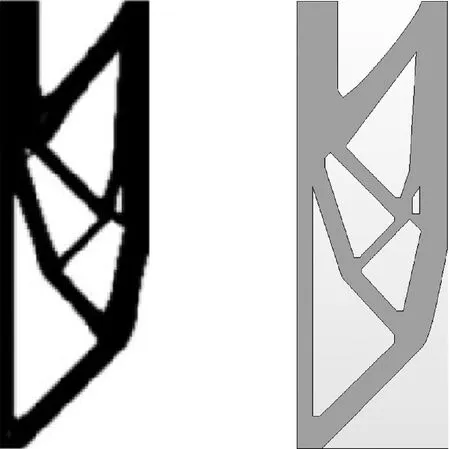
(a)-X方向優化結果 (b)-X方向分析結果圖17 -X方向優化自支撐MBB梁及分析結果 Fig.17 Optimized self-supporting MBB beam in -X direction and analysis results

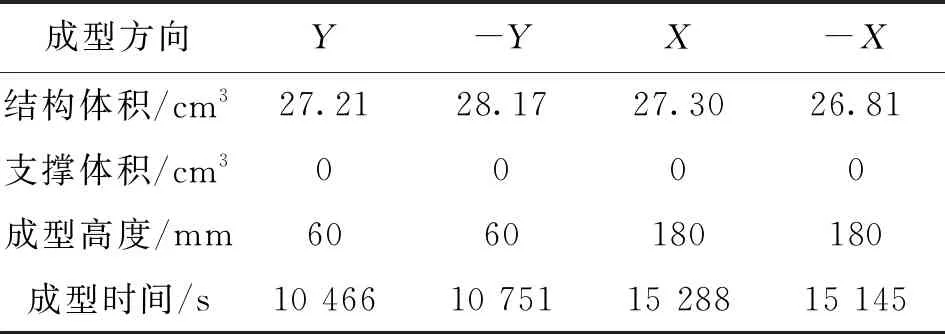
表5 自支撐MBB梁成型數據統計

4.3 對比分析

Langelaar模擬增材制造逐層堆積的成型過程,采用過濾方法優化設計自支撐結構的方法[18]受到了廣泛的認可,將本文所提方法與Langelaar方法和傳統拓撲優化方法進行對比分析,總結本文所提方法的優點和不足。

Langelaar方法在文章中從北、東、南、西4個方向優化設計同樣的MBB梁,將設計域離散為180×60個單元。表6匯總了應用3種方法的優化結果,cMBB為MBB梁柔度,cref為傳統MBB梁柔度。對比可得基于本文所提方法得到的優化結構:

(1)在結構柔度方面,與傳統拓撲優化方法相比,Y方向增大了19.9%,X方向減小了0.2%,-X方向減小了0.2%,與Langelaar優化方法相比,Y方向增大了13.1%,X方向減小了0.2%,-X方向減小了1.1%;

(2)在所需材料方面,與傳統拓撲優化方法相比,Y方向體積減小了20.6%,-Y方向體積減小了18.0%,X方向體積減小了18.1%,-X方向體積減小了20.0%;

(3)在打印時間方面,與傳統拓撲優化方法相比,Y方向減小了16.6%,-Y方向減小了14.5%,X方向減小了10.5%,-X方向減小了11.5%;

(4)在迭代步數方面,與傳統拓撲優化方法相比,Y方向增大了9%,X方向增大了129.6%,-X方向增大了163.2%。

通過對比分析,可知本文所提方法能夠沿4個方向對MBB梁進行優化設計,其中在X和-X兩個方向上的結構柔度均優于傳統拓撲優化方法和Langelaar提出的拓撲優化方法,雖然在某些方向上優化效率有所損失,但是能夠在保證結構剛度的前提下,無需使用支撐,減少打印材料和打印時間的浪費。

本文針對45°臨界角,基于SIMP變密度法,構建了面向增材制造的平面自支撐結構拓撲優化方法。基于本文所提方法未來可向:①采用可變長寬比四節點矩形單元構建臨界角可變的自支撐單元過濾方法,研究適應于臨界角可變的自支撐結構拓撲優化方法;②采用三維自支撐單元過濾方法判斷單元自支撐性,此時目標單元為1個,支撐單元為5個,將本文所提方法拓展至三維自支撐結構優化設計;③采用基于Heaviside函數的自支撐單元過濾方法,基于變密度法多材料插值模型或非均質材料插值模型,構建面向增材制造的多材料或非均質材料自支撐結構拓撲優化方法。

表6 MBB梁優化結果對比

5 結 論

本文模擬增材制造逐層堆積材料的成型過程,提出了一種基于Heaviside函數的自支撐單元過濾法則。基于SIMP變密度法構建了面向增材制造的自支撐結構拓撲優化方法,并將本文所提方法應用到MBB梁拓撲優化中。通過數值案例可得出如下結論:

(1)本文所提出的一種基于Heaviside函數的自支撐過濾法則能夠有效判斷單元自支撐性,并逐層保留自支撐單元,刪除非自支撐單元;

(2)本文所提的面向增材制造的自支撐結構拓撲優化方法能夠有效解決傳統拓撲優化結構在增材制造過程中使用支撐的問題,并且在不損失結構剛度的前提下,節省打印材料和打印時間;

(3)本文所提的面向增材制造的自支撐結構拓撲優化方法能夠在4個方向上對平面結構進行優化設計,并且可得成型方向對結構構型、剛度和優化效率有很大的影響,可依據結構使用要求選擇最優設計方案。