一種拱形線性壓電作動器的作動特性分析

曹利民，王偉，郭宗和

(山東理工大學 交通與車輛工程學院，山東 淄博 255049)

各種設備產品在工作過程中產生的振動對設備的使用性和安全性都會造成一定程度的影響，降低設備的使用效果和使用效率，減小設備在使用過程中的振動可以使設備的使用性能和安全性得到提高。王巍等[1]設計了一種新型的壓電作動器，這種作動器由一片壓電片粘貼在一個弓型梁底座上構成，使用時將底座粘貼于被控結構上，壓電片驅動弓型梁底座彎曲變形進而對被控結構產生作動效果;經過分析對比發現，拱形壓電作動器與傳統壓電片作動器相比具有更好的控制效能及良好的使用靈活性，特別是對高階模態的控制效果要優于傳統壓電片作動器，這種弓型梁構型設計在振動壓電能量收集技術上具有一定的應用潛力。Foutsitzi等[2]對用于梁結構壓電作動器的最佳電壓和最佳位置進行了數值研究，建立了基于Timoshenko梁理論的壓電作動器性能有限元模型，證明了所提出的混合遺傳算法具有確定控制作動器在可能位置內的最佳電壓和位置的能力。Wang等[3]從可控性角度出發，研究了在梁上布置壓電片的最佳位置及其尺寸，通過最大化可控性角度得出壓電作動器的優化設計指標，分析了一對壓電片作動器在各種梁上的示例，為壓電作動器的結構振動控制提供了工具，并且給出了壓電耦合結構性的定量指標。Zhang等[4]介紹了一種新的尺蚯蚓型壓電作動器，并設計了一個具有高壓驅動和閉環控制系統的實驗系統，建立了模擬動態模型；仿真結果表明，所設計的閉環控制器可以精確控制壓電作動器的動作。除此之外，文獻[5-15]分別對壓電陶瓷能量收集、三穩態能量收集、壓電作動器的控制、不同形式的新型壓電作動器以及壓電材料在其他方面的應用進行了研究。

本文研究一種新型的對設備和裝置進行變形和振動衰減的拱形壓電作動器裝置，結合卡式第二定理推導作動器輸出力表達式，并通過仿真分析進行驗證。

1 拱形壓電作動器的結構模型

高精度拱形壓電作動器的結構模型如圖1所示，該拱形壓電作動器由拱形裝置、壓電堆以及振動設備組成。其中，拱形裝置與振動設備之間以及壓電堆與拱形裝置和振動設備之間都通過環氧樹脂膠進行粘接。通過給壓電堆通入電壓可使壓電堆產生力和變形，該壓電堆產生的力和變形通過拱形裝置傳遞到振動設備上，并與振動設備產生的振動進行相互作用，從而對振動設備起到衰減變形和振動的作用。

圖1 拱形壓電作動器結構模型Fig.1 Structural model of arched piezoelectric actuator

2 拱形壓電作動器的設計

2.1 理論解計算

壓電堆通入不同的電壓時，在豎直方向上會產生大小不同的位移和作用力，將該拱形壓電作動器裝置進行簡化，其受力作用情況如圖2所示。

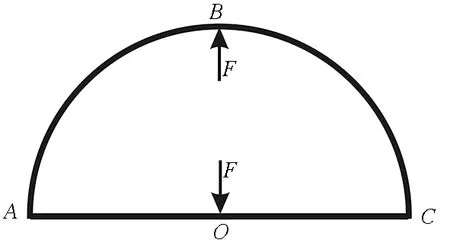
圖2 拱形裝置受力情況Fig.2 Force of arch device

因為該拱形裝置為對稱結構，所以可根據正對稱關系對結構進行簡化求解。圖2中的A處也有作用力，但由于該處是與懸臂梁的粘貼部位，對于理論計算的影響較小，因此將該處的受力給予省略，其力學簡化模型如圖3所示。下面利用卡式第二定理進行結構分析。

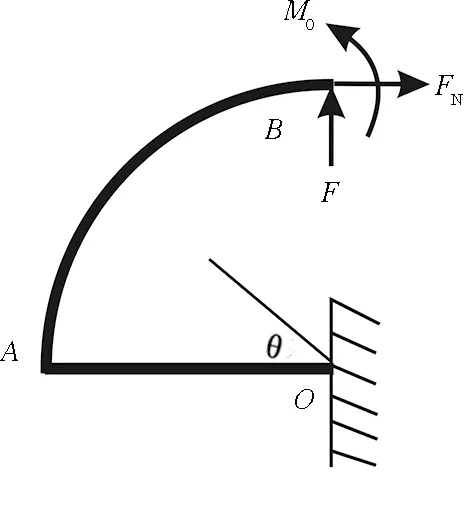
圖3 力學簡化模型Fig.3 Simplified mechanics model

根據圖3中的受力關系可知，AB段的彎矩和軸力分別為：

M1=M0+FRcosθ-FNR(1-sinθ)，

(1)

FNx=Fcosθ,FNy=FNsinθ；

(2)

AO段的彎矩和軸力分別為：

M2=-M0-FR+FNR，

(3)

FNL=FN,

(4)

式中:F為壓電堆產生的作用力;M1、M2分別為AB段和AO段的彎矩;FNx、FNy分別為AB段在水平方向和垂向的軸力;FNL為AO段的軸力;θ為拱形裝置受壓電力方向與水平方向的夾角;R為拱形半徑。

拱形結構的變形能為

(5)

式中:E1、A1、Iz1分別為拱形裝置的彈性模量、橫截面積、轉動慣量；E2、A2、Iz2分別為懸臂梁的彈性模量、橫截面積、轉動慣量。

將變形能的公式分別對M0和FN求偏導，可得：

(6)

(7)

令F=1并將其代入公式(1)至(7),可求得FN和M0。

分別對M1和M2求導得：

(8)

(9)

根據莫爾積分法可得拱形裝置在單位載荷下的位移，即

(10)

由此可求得拱形裝置的剛度

k=F/δΔ。

(11)

在壓電堆上施加電壓U后，可得壓電堆的位移，即拱形裝置在電壓U下的變形量

δ=d33nU，

(12)

式中：d33為應變系數；n為壓電片個數；U為驅動電壓。

則壓電堆在通入電壓U下所產生的力為

F=kδ，

(13)

因此作用在振動設備上的彎矩為

M=M0+FR-FNR。

(14)

拱形裝置產生的彎矩值越大，在一定的變形范圍內對振動設備的變形和振動的衰減效果也就越好。該彎矩可以將振動設備本身產生的一部分振動進行抵消，從而達到衰減變形和振動的作用。

2.2 建模仿真

將該拱形壓電作動器應用于懸臂梁上，使用ANSYS軟件對其進行建模仿真。

懸臂梁和拱形裝置的單元均為SOLID45。SOLID45單元用于構造三維固體結構，單元通過8個節點來定義，每個節點有3個沿著x、y、z方向平移的自由度；單元具有塑性、蠕變、膨脹、應力強化、大變形和大應變能力。壓電堆的單元為SOLID5，SOLID5具有三維磁場、熱場、電場、壓電場和結構場分析能力，并能在各場之間實現有限的耦合；本單元有8個節點，每個節點最多有6個自由度；壓電堆的使用型號為PZT-5A，其參數如下[16]：

剛度CE為

1010N/m2，

(15)

壓電應力常數e為

(16)

介電常數ε為

(17)

在ANSYS中輸入以上壓電堆參數，建立拱形壓電作動器以及懸臂梁模型，并進行其他材料屬性的設置和網格劃分，懸臂梁、拱形裝置和壓電堆均采用六面體網格劃分。其中，懸臂梁的尺寸為500 mm×50 mm×5 mm；拱形裝置的內半徑為17 mm，寬度為30 mm，厚度為4 mm；壓電堆的高度為12 mm，寬度為10 mm。最后給壓電堆施加電壓，進行仿真求解。

將該裝置應用于懸臂梁上，其仿真模型如圖4所示。模型懸臂梁左端為完全固定約束，各部件之間通過粘貼組合在一起，對壓電堆施加電壓后，對其進行仿真分析，其變形結果如圖5所示。

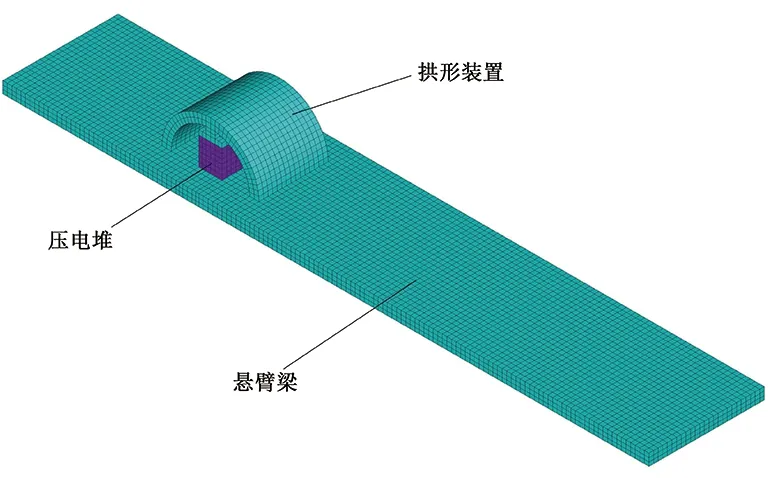
圖4 拱形壓電作動器在懸臂梁上的應用模型Fig.4 Application model of arched piezoelectric actuator on cantilever beam

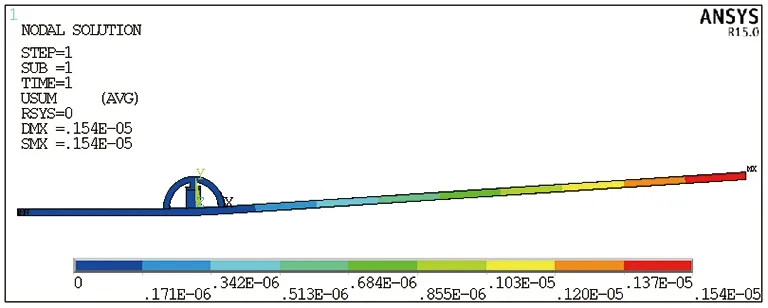
圖5 仿真變形結果Fig.5 Simulation deformation results

不斷改變通入壓電堆的電壓大小，對不同電壓下懸臂梁的變化情況進行仿真，將仿真結果與理論計算結果進行對比(如圖6所示)，發現兩者結果基本吻合，證明了理論計算的正確性。但從圖6中可以看出，仿真分析結果與理論計算結果有細小的偏差，這是由仿真分析中網格劃分的細密程度導致的。因此，仿真分析與理論計算結果是一致的。

圖6 仿真結果與理論計算結果對比圖Fig.6 Comparison between simulation results and theoretical calculations results

通過圖6也可以看出，拱形壓電作動器的作用效果與壓電堆通入電壓的大小是成正比例關系的，壓電堆通入的電壓越大，其使懸臂梁產生的位移也就越大，對于懸臂梁的變形和振動的衰減效果也就越好。

壓電堆不通電壓的情況下，在懸臂梁端部施加一個正弦載荷，將懸臂梁在該載荷下端部隨時間變化的位移與壓電堆通入電壓后同樣正弦載荷作用下懸臂梁端部隨時間變化的位移進行比較，觀察該拱形裝置所起到的振動和變形的衰減作用，其比較結果如圖7所示。

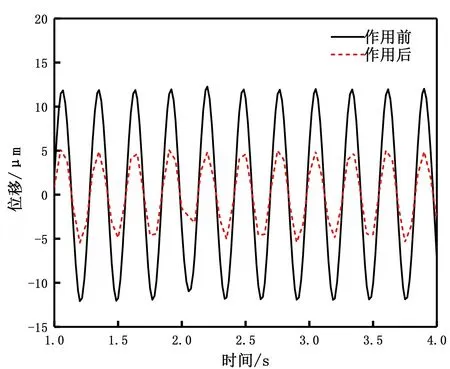
圖7 懸臂梁在正弦載荷下的端部位移Fig. 7 End displacement of cantilever beam under sinusoidal load

由圖7可以看出，拱形壓電作動器對施加正弦載荷后懸臂梁的振動和變形有一定程度的衰減作用。

壓電堆不通電壓的情況下，在懸臂梁端部施加一個沖擊載荷，將懸臂梁在該載荷下端部隨時間變化的位移與壓電堆通入電壓后同樣沖擊載荷作用下懸臂梁端部隨時間變化的位移進行比較，觀察該拱形裝置所起到的振動和變形的衰減作用，其比較結果如圖8所示。

圖8 懸臂梁在沖擊載荷下的端部位移Fig. 8 End displacement of the cantilever beam under impact load

由圖8可以看出，該拱形壓電作動器可以有效減小懸臂梁的振動幅度，對振動有一定的衰減作用，提高了懸臂梁的使用穩定性。

3 拱形壓電作動器的參數優化及分析

3.1 拱形壓電作動器的參數優化

通過對稱性可知，B點的轉角和彎矩都為0，因此有

(18)

將式(6)和式(7)化簡可得：

(19)

(20)

聯立方程組(19)和(20)并求解，可以得到軸力FN和彎矩M0分別為：

FN=(8-2π)FR2A1A2E22Iz2/(π2R2E22A1A2Iz2+

2πR2E1E2A1A2Iz2+π2E22A2Iz1Iz2+

2πE1E2A2Iz12+4πE1E2A1Iz1Iz2+

8E12A1Iz22-8R2E22A1A2Iz2)，

(21)

M0=-FR(4E12Iz12A1+πIz12E2A2E1+

πR2E2A1A2E1Iz1+8E1Iz1Iz2A1E2+

2πIz1E22Iz2A2-12R2A1A2E22Iz2+

4πR2A1A2E22Iz2)/(π2R2E22Iz2A1A2+

2πR2E2A1A2E1Iz1+π2Iz1E22Iz2A2+

2πIz12E2A2E1+4πE1Iz1Iz2A1E2+

8E12Iz12A1-8R2A1A2E22Iz2)。

(22)

引入以下無量綱參數：

(23)

在式(21)和式(22)中代入相應數據并通過式(23)對其進行化簡，得到軸力FN和彎矩M0如下：

(24)

M0=FR(1.2288×10-5α2+8.8495R2+

1.309×10-4+α(0.1508R2+1.0011×10-4))/

(2.4576×10-5α2+0.2921R2+2.0562×10-4+

α(0.3016R2+1.6588×10-4))。

(25)

通過拱形壓電作動器的仿真分析與理論計算的對比可知，該拱形壓電作動器的作用效果隨壓電堆通入電壓的增大而越來越好。因此，在壓電堆的作用下，作用在懸臂梁上的M0和FN會隨著壓電堆通入電壓值的變化而不斷變化，從而改變該拱形壓電作動器的作用效果。由公式(14)可知，當M0的數值越大、F的數值越大以及FN的數值越小時，該拱形裝置作用在懸臂梁上的彎矩也就越大，即對懸臂梁的作用效果也就越好，對懸臂梁的變形和振動的衰減能力也就越強。總的來說，當彎矩M的值越大，該裝置的作用效果越好。

3.2 材料對作用效果的影響

改變懸臂梁和拱形裝置的材料，即在表達式中改變各種材料的彈性模量，觀察在不同材料組合下拱形裝置對振動的衰減能力。不同材料的組合方式下，拱形裝置對懸臂梁產生的彎矩M見表1。

表1 拱形裝置與懸臂梁在不同材料組合下產生的彎矩Tab.1 Bending moments produced by arching device and cantilever beam under different material combinations

由表1可以看出，在不同材料的組合下，拱形裝置對懸臂梁產生的彎矩不同。拱形裝置的材料為球墨鑄鐵、懸臂梁的材料為鋁合金時，拱形裝置對懸臂梁產生的彎矩比較大，即α的值越大，拱形裝置輸出的力矩也就越大。當拱形裝置的彈性模量遠大于懸臂梁的彈性模量時，拱形裝置對懸臂梁的振動和變形的衰減能力比較強。

3.3 壓電材料類型及作用面積對作用效果的影響

改變壓電材料的類型以及壓電堆的作用面積，分析比較壓電材料的類型和作用面積對拱形裝置作用效果的影響。對使用PZT-5A和PZT-4為壓電材料的壓電堆進行分析，其中PZT-4的參數如下：

剛度CE為

1010N/m2，

(26)

壓電應力常數e為

(27)

介電常數ε為

(28)

分析結果如圖9所示。

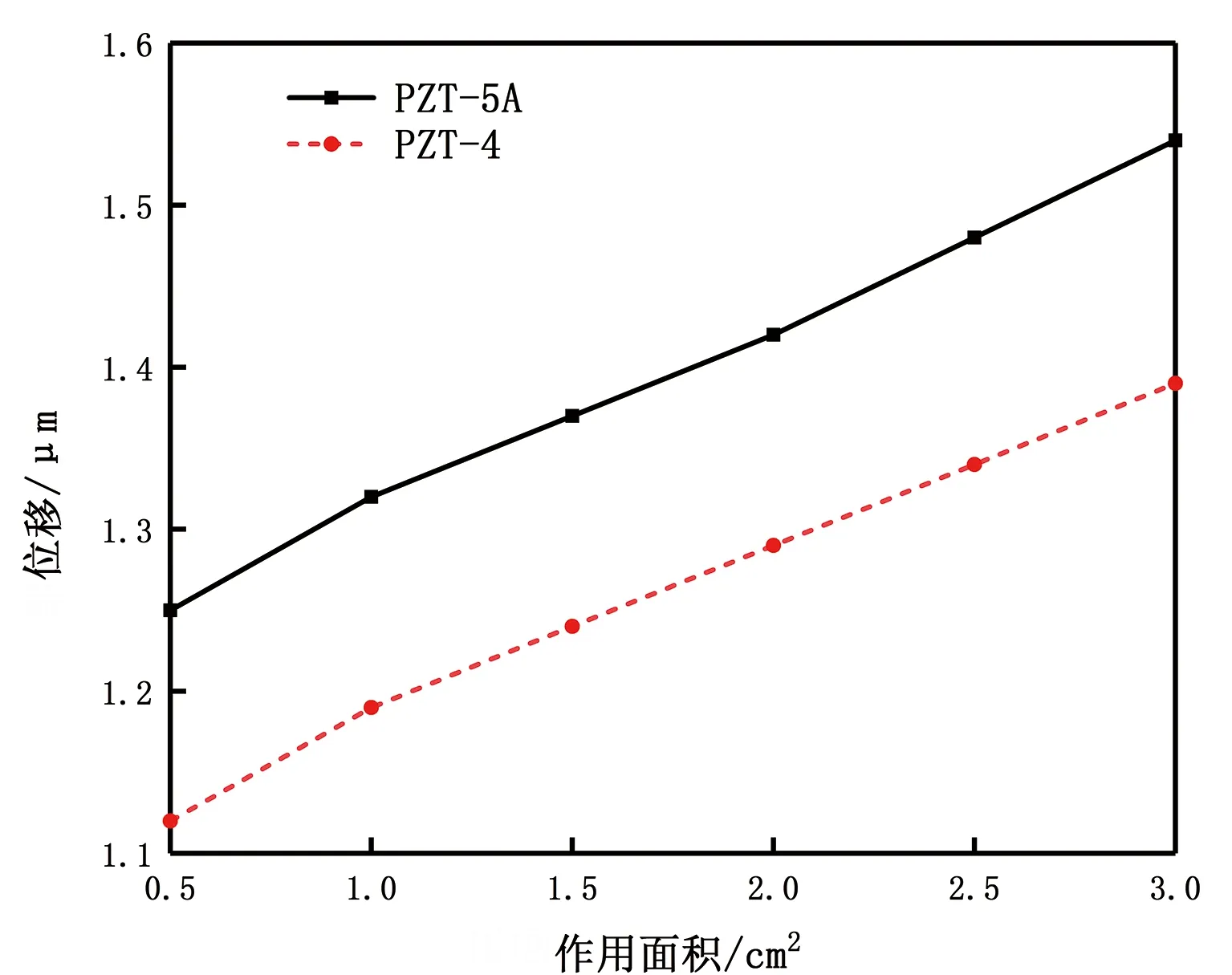
圖9 不同壓電材料和作用面積下的懸臂梁端部位移Fig.9 Displacement of the end of the cantilever beam under different piezoelectric materials and active areas

壓電應力常數是衡量材料壓電效應強弱的參數，它直接關系到壓電輸出的靈敏度。由圖9的仿真分析結果可以發現，在兩種不同壓電材料的壓電堆中，PZT-5A的作用效果要優于PZT-4的。

壓電堆的作用面積越大，對于裝置的作用效果越好。從圖9中可以看出，兩種壓電材料的壓電堆在不同作用面積下作用效果的變化規律是一樣的，因此由一種壓電材料的變化規律即可得到其他壓電材料的壓電堆在不同作用面積下的變化規律。

3.4 電壓對作用效果的影響

在不同的電壓下，壓電片通過拱形裝置對懸臂梁粘接處所產生的彎矩M的變化如圖10所示。

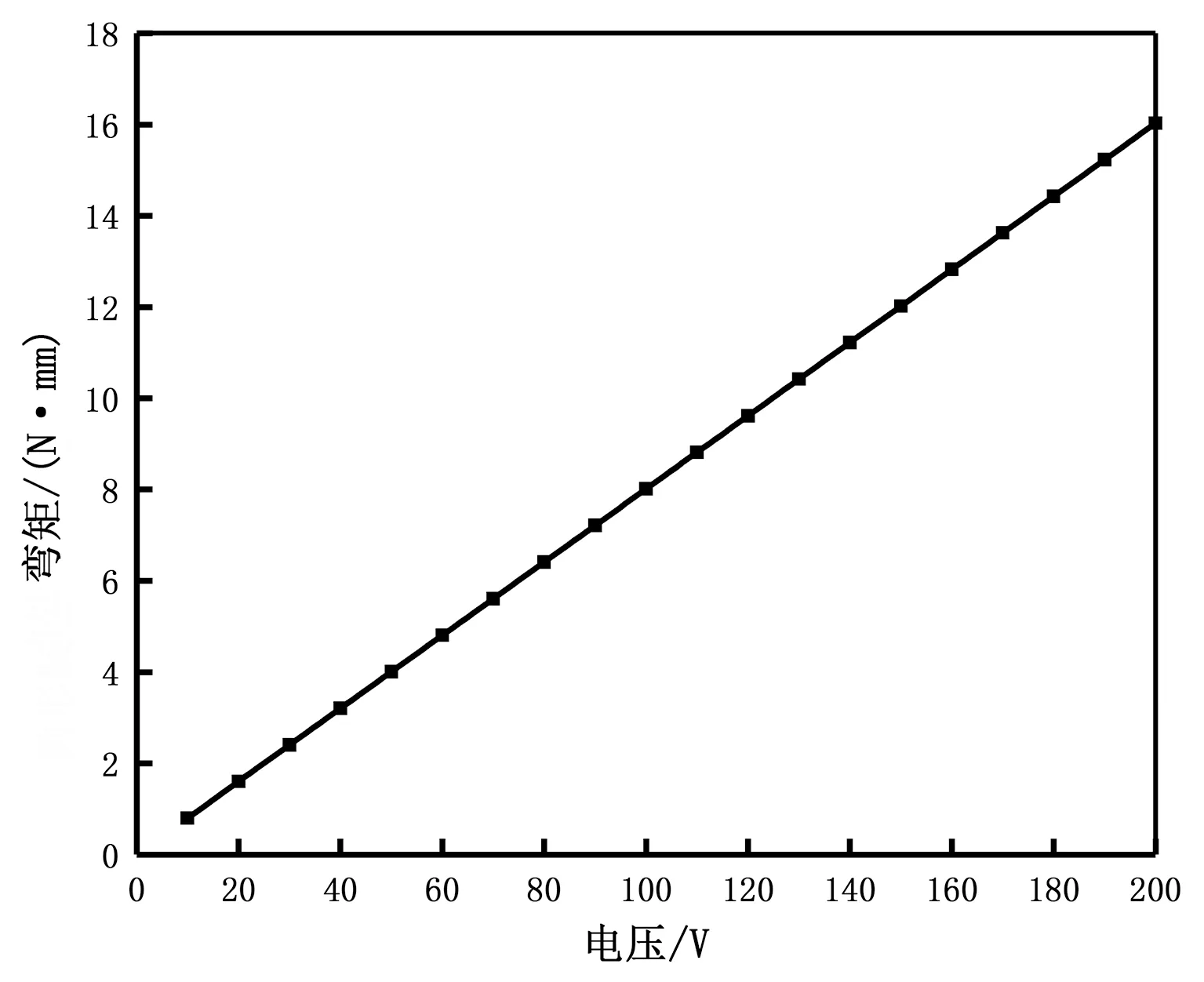
圖10 拱形裝置產生的彎矩隨電壓的變化Fig.10 Variation of bending moment produced by arched device with voltage

由圖10可知，該拱形裝置對懸臂梁產生的彎矩隨著對壓電堆施加電壓的增大而增大，說明壓電堆通入的電壓越大，對懸臂梁振動衰減的效果也就越好。

3.5 半徑對作用效果的影響

在懸臂梁和拱形裝置材料屬性和其他參數不變的情況下改變拱形裝置的跨度，即改變半徑R，觀察拱形裝置在不同的半徑下對懸臂梁產生的彎矩作用。半徑大小的影響如圖11所示。

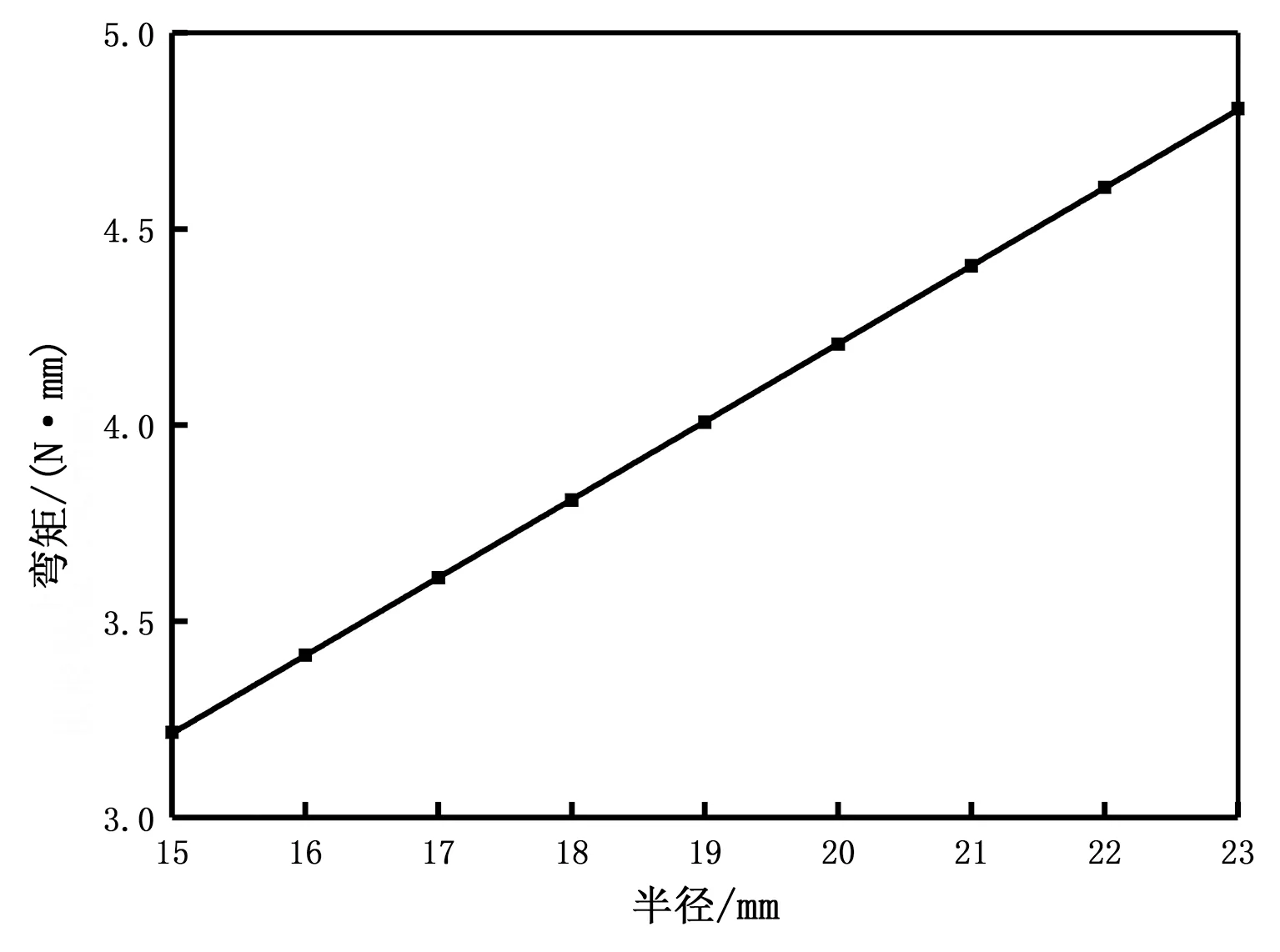
圖11 拱形裝置半徑對懸臂梁產生的彎矩Fig.11 The bending moment of the radius of the arched device on the vibration equipment

由圖11可知，拱形裝置的半徑越大，其對懸臂梁產生的力矩也就越大，作用效果也就越好。但是半徑也不是越大越好，半徑越大，拱形裝置的體積也就越大，所占空間也就也大。因此，要整體考慮半徑對懸臂梁的適用性。

通過對拱形裝置的參數進行優化，可以找到在不同情況下更加適合的參數，使拱形裝置在使用過程中能夠有更好的作用效果。

4 結論

本文針對拱形壓電作動器進行了結構分析和參數優化，使得該裝置在振動衰減過程中能夠發揮更好的振動和變形的衰減效果。結論如下：

1)在拱形裝置材料的彈性模量遠大于懸臂梁的彈性模量時，拱形裝置對振動和變形的衰減作用越好。

2)不同壓電材料對裝置的作用效果不同，PZT-5A的作用效果要好于PZT-4的作用效果。

3)壓電材料的作用面積越大，拱形裝置的作用效果越好。

4)拱形裝置的半徑不同，對振動和變形的衰減效果也不同。拱形裝置的半徑越大，對振動和變形的衰減效果也就越好，但是半徑的大小也要根據懸臂梁的實際尺寸來確定。

5)從壓電材料的正壓電效應來看，該拱形壓電作動器在進行振動能量收集方面有一定的發展潛力，可以對振動能量進行回收利用，提高能源的利用效率。