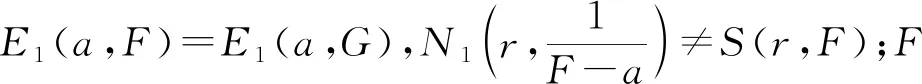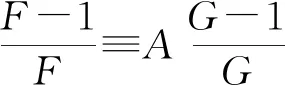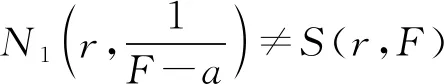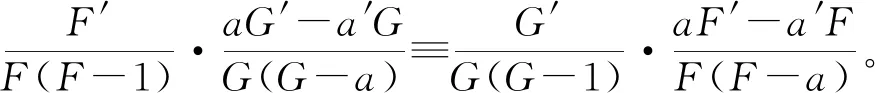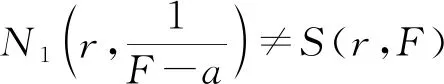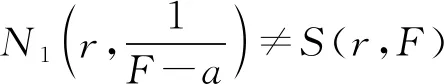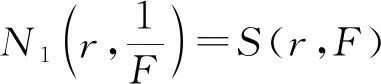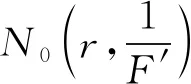涉及導數分擔小函數的亞純函數的唯一性
胡 嵐,符方健,李 倩
(1.四川財經職業學院 通識與人文教育學院,成都 610000;2.瓊臺師范學院 理學院,海口 571127)
0 引言
本研究使用值分布論的基礎知識及Nevanlinna常用理論的標準符號[1-2],其中:對于復平面上的亞純函數f(z),其涉及到的符號S(r,f)表示任意滿足S(r,f)=o{T(r,f)}(r→∞)的量,可能除去r的一個線性測度有限集合,且它每次出現并不一定相同。如果亞純函數a(z)滿足等式T(r,a)=S(r,f),那么稱a(z)為f(z)的一個小函數。設f(z)與g(z)為復平面上的兩個非常數亞純函數,小函數a(z)稱為亞純函數f(z)與g(z)的CM(或IM)公共小函數,當且僅當在計重數(或不計重數)的情況下,f(z)-a(z)與g(z)-a(z)具有公共的零點。
用Ek(a,f)表示f(z)-a(z)的k(∈+正整數集)重零點(重級零點按其重數計算)的集合,Ek)(a,f)表示f(z)-a(z)的m(≤k)重零點的集合,即Ek)(a,f)=∪Em)(a,f)。E(k(a,f)表示f(z)-a(z)的n(≥k)重零點的集合。Ek(a,f)=Ek(a,g)表示f(z)-a(z)的k重零點當且僅當它是g(z)-a(z)的k重零點。用
分別表示相應集合Ek(a,f),Ek)(a,f)與E(k(a,f)的密指量
其中:
f(z)與g(z)權分擔(a,k)表示f(z)-a(z)與g(z)-a(z)具有公共的零點,當m≤k時,若z*是f(z)-a(z)的m重零點當且僅當z*是g(z)-a(z)的m重零點;當時m>k,若z*是f(z)-a(z)的m重零點當且僅當z*是g(z)-a(z)的n(n>k且n不一定等于m)重零點。因此,f(z)與g(z)的IM或CM的公共小函數,可以表示為f(z)與g(z)的權分擔(a,0)或(a,∞)。
定理A[2]2(Nevanlinna第一基本定理) 設f(z)為區間|z| 定理B[2]18(對數導數引理)設f(z)為復數域上的非常數亞純函數,則 本研究主要利用值分布論的基礎知識,將隨機微分方程作為一種重要的數學工具(主要參考了文獻[3-5]),探討導函數的唯一性定理。 1964年,楊樂研究導函數的唯一性,得到了如下關于亞純函數導函數的4CM值定理。 定理C[6]設f(z)與g(z)為復平面上兩個超越亞純函數,k為正整數,aj(j=1,2,3,4)為四個判別的有窮復數,若aj(j=1,2,3,4)為f(k)(z)和g(k)(z)的CM公共值,則f(k)=g(k)。 2012年,韓俊峰等人改進上面的結論,通過研究兩個亞純函數的k階導數在涉及截斷分擔一個公共值的情況下得到了以下導函數的唯一性定理。 定理D[7]設f(z)與g(z)為復平面上的兩個非常數亞純函數,k∈+,aj(j=1,2,3,4)為四個判別的有窮復數,f(k)與g(k)分擔a1,a2CM;f(k)與g(k)權分擔(a3,1),E1(a4,f(k))=E1(a4,g(k))。若是則有f(k)=g(k)。 本研究將定理D中關于兩個亞純函數的導數分擔公共值問題改進為分擔公共小函數的情況,得到了改進的導函數的唯一性定理。 為了證明主要結果,需要引入以下引理。 引理1[8]設f(z)與g(z)為判別的非常數亞純函數,aj(j=1,2,…,q)為f(z)與g(z)的q個互相判別的小函數,則對于任意的ε>0,有 其中:r?E,E?R且?Edlog(logr)<∞。 引理2 設f(z)與g(z)為判別的非常數亞純函數,aj(j=1,2,3)為f(z)與g(z)三個互相判別的小函數,如果aj(j=1,2,3)為f(z)與g(z)的IM公共小函數,那么有 S(r,f)=S(r,g)=S(r)。 證明由引理1可知 由此可得引理2。 引理3 設aj(j=1,2,3,4)為非常數亞純函數f(z)與g(z)的四個判別的IM分擔小函數,如果f(z)?g(z),那么有 證明由引理1與引理2可知 即T(r,f)≤T(r,g)+S(r)。同理可得T(r,g)≤T(r,f)+S(r)。故有 T(r,f)=T(r,g)+S(r)。 由定理A與上式可知 引理4[9]f(z)為一個非常數亞純函數,若是aj(j=1,2)為f(z)與g(z)兩個互相判別的小函數且 則有 定理1 設f(z)與g(z)為復平面上的兩個非常數亞純函數,k∈+,aj(j=1,2,3,4),為f(k)與g(k)的四個判別的公共小函數,f(k)與g(k)分擔a1,a2CM;f(k)與g(k)權分擔(a3,1),E1(a4,f(k))。若有則有f(k)=g(k)。 證明令 則由命題中條件可得: 由引理2可知 S(r,F)=S(r,G)=S(r)。 令 (1) (2) 因此由式(1)可見,在F(F-1)的零點處,Δ1解析;F的極點處,Δ1解析。故有 N(r,Δ1)=S(r) , (3) 從而由定理B可知 m(r,Δ1)=S(r) , (4) 由定理A、式(3)和式(4)式可知 T(r,Δ1)=S(r) 。 (5) 類似地,由式(2)可知,Δ2在F(F-1)的零點處解析,在F與G的單重極點處也解析。故有 (6) 由定理B可知 m(r,Δ2)=S(r) , (7) 故由定理A、式(6)和式(7)可知 (8) 可以斷言Δ1≡0或Δ2≡0。事實上,如果假設有Δ1?0且Δ2?0成立。 注意到:如果z∞為F的p(≥2)重極點,且為G的q(≥2)重極點,則z∞為Δ1的零點。 當Δ1?0時,有 (9) 當Δ2?0時,有 (10) 由式(8)和式(10)可知 (11) 由式(9)和式(11)可知 當Δ1≡0時,也即 (12) 對式(12)積分可得 當Δ2≡0時,也即 (13) 由式(13)可知:∞為F與G的CM分擔值,a為F與G的IM分擔值。又因E1(a,F)=E1(a,G),故F與G的權分擔為(a,1)。令 (14) 即 (15) 則由引理4可知 m(r,Δ3)=S(r)。 (16) 以下對Δ3分兩種情況進行討論。 (I)若Δ3≡0,則 情況1 當F≡G時就有f(k)=g(k)。 情況2 當有 (17) 成立時,由式(13)可知 (18) 由式(17)和式(18)可得 (19) 對式(19)進行積分可得 F=AG(其中A為非零常數)。 (II)若Δ3?0,結合式(18)可知 由0,1,∞為F與G的CM分擔值,可知0,1,∞為Δ3的解析點。 假設za為F-a的p重零點,且為G-a的q重零點,但不是a和a-1的零點和極點。不失一般性,不妨設p≤q,由式(14)可知:za為Δ3的右端第一個分式中分子的至少p+q-1重零點,為Δ3的右端第一個分式中分母的q重零點,為Δ3的右端第二個分式中分子的至少2p-1重零點,為Δ3的右端第二個分式中分母的p重零點。從而可知za為Δ3的至少p-1(≥0)重零點,故za不是Δ3的極點。 綜合以上分析可得 N(r,Δ3)=S(r)。 (20) 由定理A、式(16)和式(20)可知 T(r,Δ3)=S(r)。 (21) 由F與G權分擔(a,1)及式(15)可知:F-a的p(≥2)重零點,G-a的q(≥2)重零點均是Δ3的零點。由式(21)可知 (22) (23) 即可得到a為F與G的CM公共小函數。 設Z0為F的m(≥2)重極點或F(F-1)的n(≥2)重零點,則z0為Δ3的零點。由式(21)可知 (24) (25) (26) 由引理3可知 (27) 由N1(r,F)=S(r)及式(22)—式(27)可知 (28) (29) (30) 令 因1與∞為F與G的CM公共值,故在F-1的零點處,α解析;在F的極點處,α解析。故有 (31) 由引理1可知 (32) (33) 由式(32)和式(33)可知 由上式可知 (34) 再由式(30)、式(31)和式(34)可知 N(r,a)=S(r), (35) 由此及定理B可知 m(r,α)=S(r), (36) 因此,由定理A、式(35)和式(36)可知 T(r,α)=S(r)。 (37) 若α?0,設z1為F-1的1重零點,且為G-1的1重零點。則z1為α的零點。故由式(37)可知 (38) 若α≡0,則 對上式進行兩次積分可得 (39) 又因0,a為F與G的CM分擔,故A=1且B=1。由式(39)可知F=G,即f(k)=g(k)。 (40) (41) 因0,1,∞,a均為F與G的CM分擔,故 N(r,H1)=S(r),N(r,H2)=S(r), (42) 由定理B可知 m(r,H1)=S(r),m(r,H2)=S(r)。 (43) 由定理A、式(42)和式(43)可知 T(r,H1)=S(r),T(r,H2)=S(r)。 (44) 若H1?0,令z1為F-1的1重零點,且為G-1的1重零點,則H1(z1)=0。故z1為H1的零點。因此有 若H2?0,令z0為F的1重零點,且為G的1重零點,則H2(z0)=0。故z0為H2的零點。這時也有 若H1≡0且H2≡0,由式(40)和式(41)可知 (45) 由式(13)和式(45)可得 a(1-a)(F-G)≡0。 (46) 又由于a≠0,1,故由式(46)可知F=G,即f(k)=g(k)。
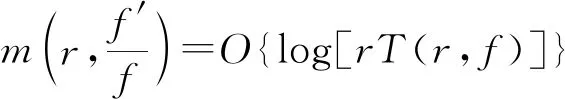
1 幾個引理
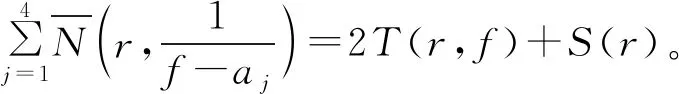
2 主要結果及其證明