基于Petri網的消防機器人任務分配及路徑規劃方法

何舟，張瑞杰，劉苗，古嬋

(陜西科技大學 機電工程學院，陜西 西安 710021)

0 引 言

消防機器人作為一種具有滅火救援功能的特種機器人，可以代替人類到較為危險的環境中展開工作[1]。因此，如何規劃其路徑軌跡并高效協同完成相應任務已經逐漸成為機器人協同工作的研究熱點。

文獻[2]提出了一種有限概率狀態模型，并結合Petri網采用一種在線策略隨時調整偏離軌跡的機器人，適合于具有更為復雜任務的機器人系統。文獻[3]采用布爾規范將多機器人任務進行描述，將布爾任務轉化成整數線性規劃問題來求解，最終得到滿足任務的最短軌跡。現有文獻主要是對單個或多個獨立的機器人采用如遺傳算法[4]、蟻群算法[5]和粒子群算法[6]等進行路徑優化。文獻[7]提出一種基于動態慣性權重的改進粒子群算法，可以在較復雜的環境下規劃出一條平滑安全無碰撞路徑。文獻[8]在傳統蟻群算法的基礎上引入信息素的模糊控制更新方式，對狀態轉移概率函數進行改進，有效減少了迭代的次數并且得到消防機器人更優的路徑。

目前，越來越多的消防機器人已應用到各種危險場合，消防機器人的廣泛應用對其路徑規劃能力提出了更高的要求[9]。本文提出了一種基于Petri網的任務分配及最優路徑規劃方法。通過構建Petri網模型對消防機器人工作環境進行描述，在此基礎上通過求解整數線性規劃獲得消防機器人協同工作時間最短的路徑，確保救援的高效性。

1 Petri網基礎

一個Petri網可定義為一個四元組N=(P，T，F，W)，其中:P={p1，p2，...，pn}為n個庫所的集合；T={t1，t2，…，tm}為m個變遷的集合；F?(P×T)∪(T×P)，稱為有向弧的集合;W為F→N，稱為網N的權函數，N={0，1，2，…}。W(p，t)為從p到t的權值，W(t，p)為從t到p的權值。

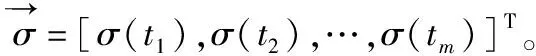
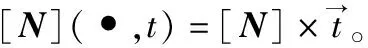
(1)

式(1)稱為Petri網的狀態方程，表示標識和變遷序列中變遷出現次數的關系。

2 消防機器人協同任務分配及路徑規劃

2.1 工作環境建模

本文參考文獻[10]的室內仿真環境，如圖1所示，對其進行區域劃分和調整后得到圖2所示的消防機器人工作環境。各機器人既可以和中央通信也可以互相通信，圖2的工作空間被劃分成若干個小房間，房間與房間之間通過雙向門連接，實現雙向移動。這樣任務分配的問題就轉變成控制指定功能和數量的機器人到達指定的房間完成相應的任務。

圖1 多機器人室內救援環境

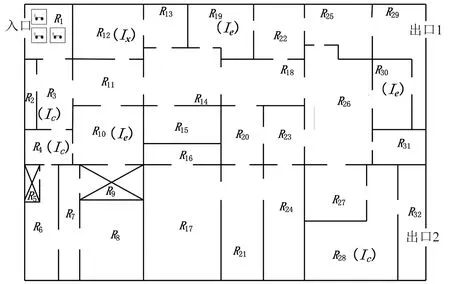
圖2 消防機器人工作環境

圖1中存在兩個機器人、障礙物以及不可通行的墻壁，其利用2個機器人同時進行掃描工作，實現對該環境的地圖構建，從而指引救援人員實施救援工作。

圖2的每個區域Ri被認為是一個庫所，記做pi(i=1，2，…，n)；機器人從區域Ri到達區域Rj通過變遷tk(k=1，2，…，m)來表示。因此，圖2的Petri網模型如圖3所示。

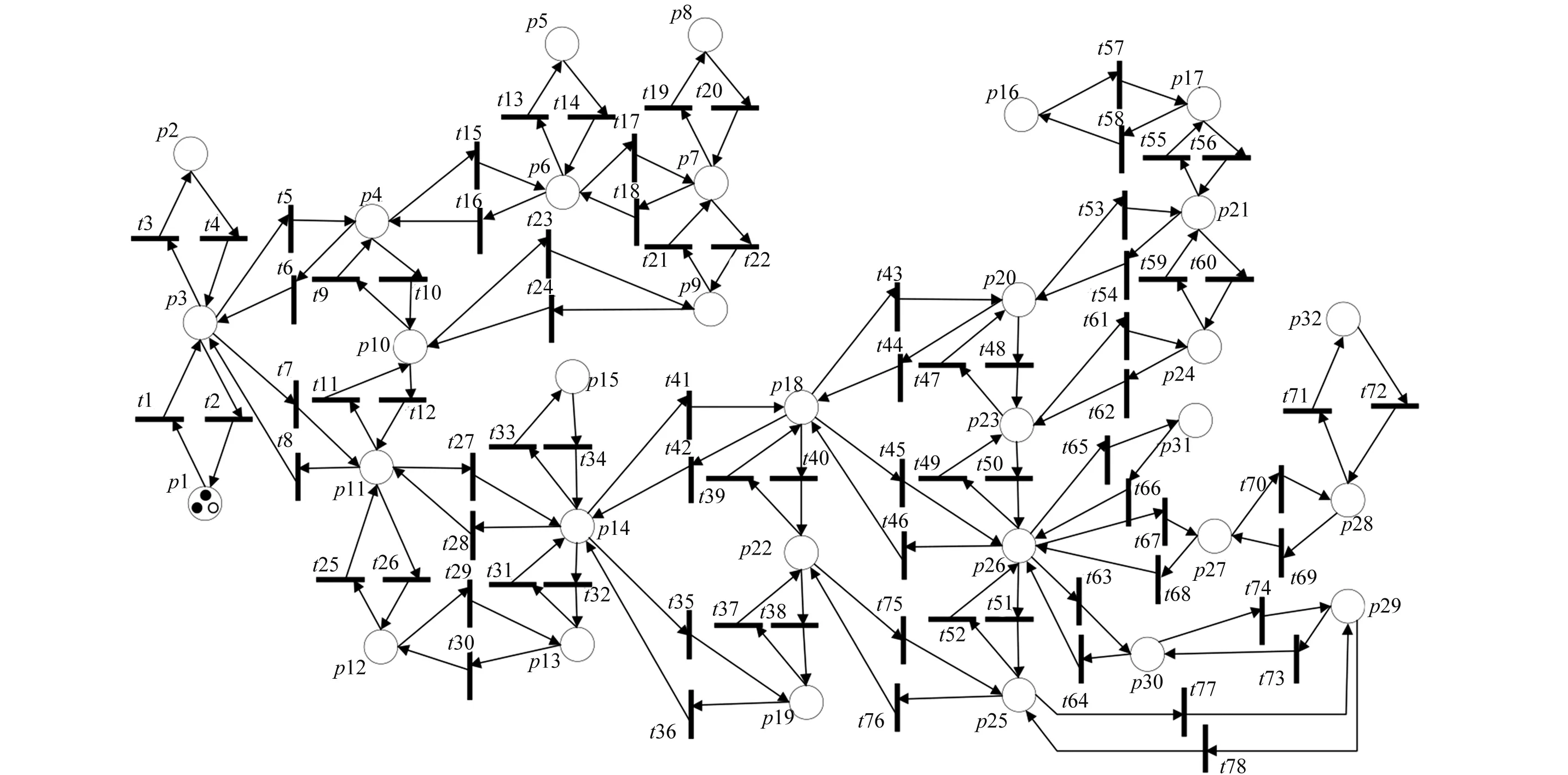
圖3 消防機器人工作的Petri網模型

2.2 消防機器人協同工作

本文將消防機器人工作環境分為：公共區域、專屬區域、協同區域、避障區域和終點區域。公共區域是所有機器人都可以進行訪問的區域；不同類型的機器人有各自的專屬區域，該區域只能由對應機器人訪問；協同區域是多機器人共同執行任務的區域；避障區域是任何機器人都無法訪問的地方；終點區域是機器人最終到達的位置。

由于基本Petri網里面的資源是相同的，當某個變遷觸發時，對應的具體是哪個機器人進行移動并不能很好地區分開來。如果要在基本Petri網中對資源進行區分，就需要為每一個機器人單獨建立一個基本Petri網模型。當環境中的機器人數量很多時，模型的規模會大幅增加，不便于表示和分析。考慮到每個機器人的工作環境模型是相同的，本文將同一工作環境下不同種類的機器人的路徑使用不同的線型進行區分，并將每種類型的機器人路徑分成H步計算，以此來解決區分機器人所帶來的基本Petri網規模膨脹問題。

假設圖1的工作環境有3種不同類型的消防機器人，記為r1、r2、r3。現有3個專屬任務和1個協同任務需要這3個機器人完成：

專屬任務1：需要在p10處由r1類型的機器人獨立完成。

專屬任務2：需要在p30處由r2類型的機器人獨立完成。

專屬任務3：需要在p19處由r3類型的機器人獨立完成。

協同任務：需要在p12處由r2和r3類型的機器人共同完成。

機器人從一個區域移動到另一個區域記作一步，且所有機器人的初始位置均在區域R1中。假設機器人從R1出發，移動到終點區域共需要H步。r1、r2、r3的公共區域是R3、R4和R28,避障區域是R5和R9，終點區域是R29、R32。由于消防機器人工作的特殊性，到達R12的機器人的時間應該一致。

3 整數線性規劃模型的建立

3.1 模型的條件

(1)消防機器人總數量為K。

(2)機器人完成任務的最大步數為H。

(3)消防機器人的公共區域為Ic，專屬區域為Ie，協同工作區域是Ix，終點區域是If，禁行區域是Ia。

(4)消防機器人在專屬區域工作的機器人集合為Eti即完成專屬任務i的機器人集合，其中：i=1，2，…，n。協同區域的機器人集合為Ex。

(5)消防機器人的運行環境較為寬松，允許多個機器人在一個房間中。

3.2 模型的建立過程

為實現高效救援工作，本文以消防機器人的工作時間最短為優化目標。在Petri網中，令f=[f(t1)，f(t2)，…，f(tm)]∈Nm，給每個變遷賦值一定的時間。優化目標函數式(2)使所有機器人工作總時間最短：

(2)

消防機器人r在第h步的位置變化可由狀態方程(1)得式(3)：

(3)

消防機器人r在第h步變遷使能后庫所內的托肯數非負，則有式(4)：

(4)

機器人r第h步只能到達一個位置，即第h步最多只會觸發一個變遷，則有式(5)：

(5)

公共區域作為所有消防機器人都可以訪問的區域，應保證至少有一個機器人對其進行訪問，則有式(6)和式(7)：

(6)

(7)

式中：vRj=[vRj(p1)，…，vRj(pn)]是一個包含n個元素的向量，每個元素vRj(pi)是一個0～1變量。當機器人訪問區域Rj的時候，該向量只有第j個元素為1，即：

(8)

消防機器人的專屬區域只能由對應類型的機器人進行訪問和工作，其他類型機器人不能到達該區域，應滿足式(9)和式(10)。

(9)

(10)

消防機器人的協同區域，除了對應的機器人進行訪問外，其他機器人不能到達該區域，應滿足式(11)和式(12)：

(11)

(12)

消防機器人至少會到達一個停止區域，式(13)到式(16)滿足該目標。

vRj×Mr,H-1≤zj,r×H,?Rj∈If

(13)

1-vRj×Mr,H≤zj,r×H,?Rj∈If

(14)

zj,1+zj,2+…+zj,k≤K,?Rj∈If

(15)

(16)

式中：H為一個足夠大的數；zj，r(r=1，…，K)為一個0-1變量，表示機器人r是否訪問區域Rj，即：

(17)

消防機器人應避免到達障礙區域，應滿足式(18)：

(18)

消防機器人的時刻描述：

(19)

τr,0=0

(20)

式中：τr，0為機器人的初始時刻；τr，h為機器人第h步的時刻。

4 試驗結果

基于3.2小節所建立的模型，其中，K=3，H=10，f=1，Ic={R3，R4，R28}；If={R29，R32}；Ie={R10，R30，R19}；Ia={R5，R9}；Ix={R12}；Ex={r2，r3}；Et1={r1}；Et2={r2}；Et3={r3}。MATLAB仿真得到如下結果：

r1軌跡：R1→R3→R4→R10→R11→R14→R18→R26→R27→R28→R32

r2軌跡：R1→R3→R11→R12→R13→R14→R18→R26→R30→R29

r3軌跡：R1→R3→R11→R12→R13→R14→R19→R22→R25→R29

滿足所有消防機器人完成對應任務的路徑如圖4所示，且工作時間最短為28 s。

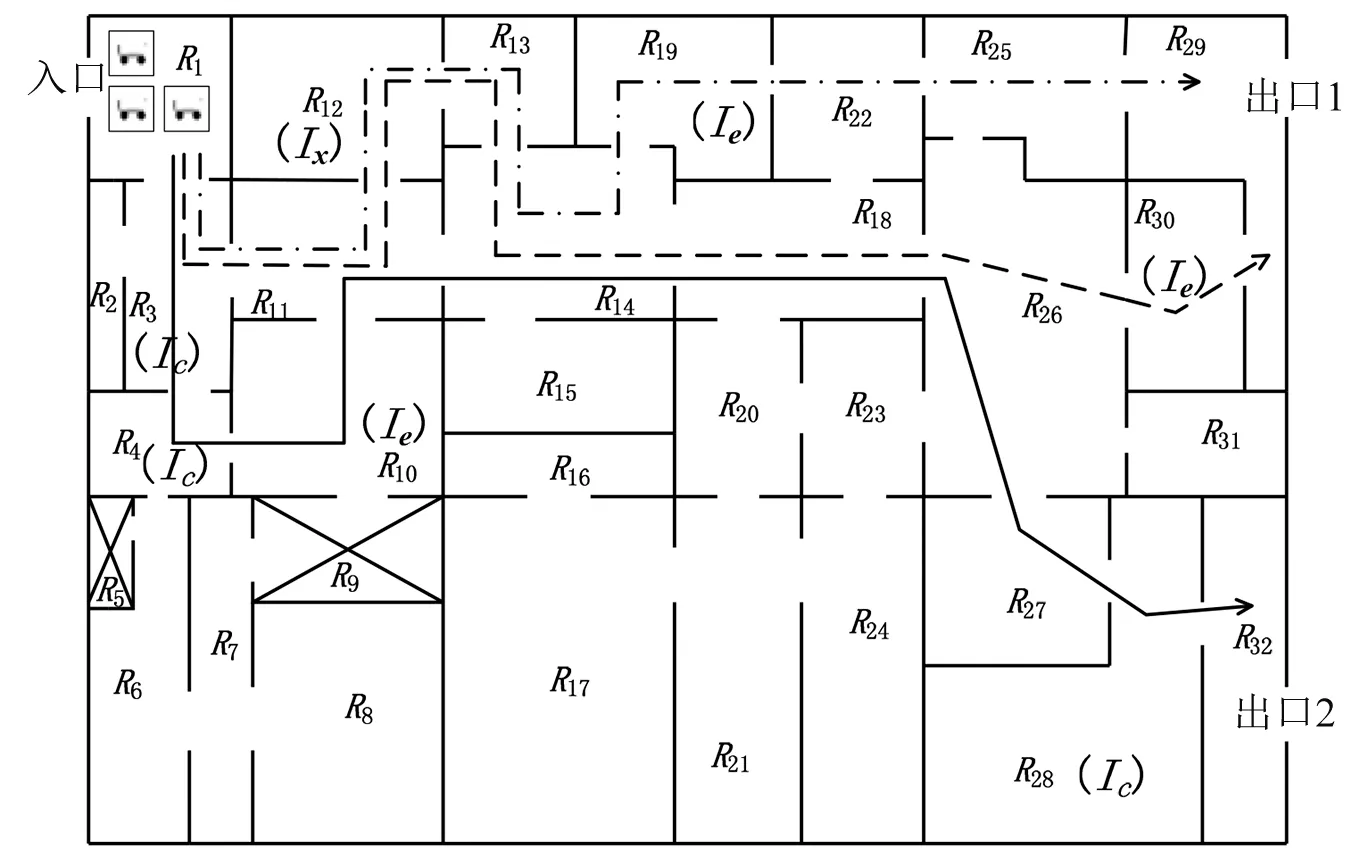
圖4 消防機器人最優路徑

5 結束語

結合消防機器人工作環境的Petri網模型，本文提出了一種基于Petri網特性的整數線性規劃方法。通過將消防機器人的工作環境劃分為公共區域、專屬區域、協同區域、避障區域和終點區域，實現了機器人的任務分配。在此基礎上，本文將對應的任務需求轉換為具有Petri網特性的整數線性規劃模型，然后利用MATLAB仿真獲得消防機器人工作效率最高的最優路徑。經驗證，本文提出的整數線性規劃方法具有可行性且計算效率高，能夠獲得消防機器人完成救援工作的全局最優路徑，確保了救援的高效性。