約束秩虧間接平差模型的虛擬觀測算法
謝 波,肖東升
(1.合肥職業技術學院 建筑工程學院,安徽 合肥 238000;2.西南石油大學 土木工程與測繪學院,四川 成都 610500)
在測量平差時,如果控制網沒有起算數據,則此時建立的間接平差模型的系數矩陣列秩虧,法方程系數矩陣也會出現秩虧。為了得到秩虧的間接平差模型的最小二乘唯一解,進行大地測量數據處理時往往會利用參數間存在的一些已知的先驗信息建立約束條件,此時建立的平差模型為約束秩虧間接平差模型[1-4]。
約束秩虧間接平差模型廣泛應用于大地測量數據處理中,其算法引起較多研究。目前,其算法主要分為:①對參數估計修正的有偏估計方法,如嶺估計和主成分估計[5-8]。由于引入了未知的嶺參數、需要確定主成分的個數等,是一個迭代計算過程;②對秩虧間接平差模型的法方程系數修正的虛擬觀測法[9-10]、參數分類法[11-12]、正則化法[13-15]、截斷奇異值法[16-17]。該類方法需要確定虛擬觀測值的權、正則化因子和截斷奇異值個數等,計算過程比較復雜;③對約束秩虧間接平差模型的分塊法方程系數矩陣求逆的廣義逆矩陣法[18-19]、直接法[20-21]等。該方法具有相對計算簡單、結果準確等特點,但是缺少更深入研究。
本文提出利用矩陣運算推導約束秩虧間接平差模型的分塊法方程系數矩陣求逆的直接顯性表達式,并提出消除秩虧間接平差模型的法方程系數矩陣秩虧的虛擬觀測算法,用數據實驗驗證直接顯性表達式和虛擬觀測算法的正確性。該方法為約束秩虧間接平差模型的算法提供了新的方法和思路。
1 約束秩虧間接平差模型的一般解析式
約束秩虧間接平差模型表示為:
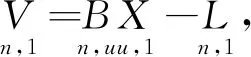
(1)
(2)
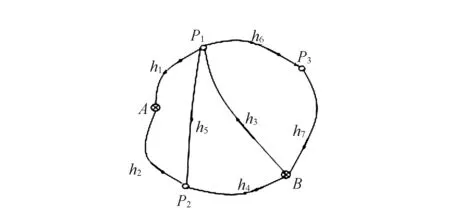
式中:V為n維觀測誤差向量,E(V)=0,D(V)=σ2P-1,B為誤差方程的n×u設計矩陣,R(B)=t 利用條件極值的拉格朗日乘數法構建函數: φ=VTPV+2KT(CX-WX)=min . (3) 式中:K為對應于約束方程的聯系數向量。為求φ的極小值,將其對x求偏導并令其等于零,則可以得到法方程: NX-W+CTK=0 . (4) 式中:N=BTPB,W=BTPL。N為u×u階秩虧矩陣,R(N)=R(B)=t 聯立式(2)和式(4),得到約束秩虧間接平差模型的總法方程為: (5) 式中:由于C為行滿秩矩陣,且R(C)=s≥u-t,根據分塊矩陣的性質[22],系數矩陣的凱利逆存在,解得: (6) 子塊矩陣N的凱利逆不存在,因此,常規的分塊矩陣的求逆式不能直接應用。 設 (7) 滿足 (8) 則 NQ11+CTQ21=Iu, (9) (10) (11) CQ12=Is. (12) 將式(11)左乘CT后和式(9)相加,可得: (N+CTC)Q11+CTQ21=Iu. (13) 同理,將式(12)左乘CT再和式(10)相加,可得: (14) 可得: (15) 式中:由于C為行滿秩且R(C)=s≥u-t,根據矩陣秩分解的性質[23],矩陣N+CTC,C(N+CTC)CT的凱利逆必存在,左邊的四分塊矩陣的凱利逆存在,可以直接應用常規的分塊矩陣的求逆式,得到分塊矩陣的逆矩陣為: (16) 分塊矩陣 (17) 將式(17)帶入式(6),可得: (18) 展開: (N+CTC)-1CT[C(N+CTC)CT]-1C(N+ CTC)-1}BTPL+(N+CTC)-1CT[C(N+ CTC)CT]-1WX, (19) 即為約束秩虧間接平差模型參數估計的一般顯性表達式。 和約束間接平差模型的參數估計公式比較,約束秩虧間接平差模型的參數估計和其在形式上完全一致,只是秩虧的法方程系數N被N+CTC代替了。因此,將約束條件看做虛擬觀測,和秩虧間接平差模型的誤差方程組合新的誤差方程: (20) (21) 設 (22) 可簡化為: (23) 方程系數和常數項為: ΒTPΒ+CTC=N+CTC, (24) ΒTPL+CTWX=W+CTWX. (25) 新的誤差方程和約束方程再構成約束間接平差模型,解算得: (26) 結果和約束秩虧間接平差模型的結果一致。因此,在約束秩虧間接平差模型解算時,將約束條件看做虛擬觀測,和秩虧間接平差模型組合成新的誤差方程之后,再和約束條件進行約束間接平差,其參數估計的結果不變。本文算法為約束秩虧間接平差模型的虛擬觀測法。 為驗證本文推導的求逆公式和虛擬觀測算法的正確性,本文選取某水準網為例進行數值驗證。如圖1所示,點A,B為已知的高程點HA=6.250 m,HB=7.250 m,點P1,P2,P3為待求的高程點,已知數據與觀測數據列于表1。 圖1 水準網 表1 觀測數據和已知數據 現分別用間接平差模型、約束秩虧間接平差模型的求逆公式法和虛擬觀測法3種不同方法來解算待求點P1,P2,P3的高程。 方法一:用間接平差模型解算上述平差問題。考慮A,B為已知點,設P1,P2,P3點的高程為未知參數x3,x4,x5,將所有觀測值的改正數表示成未知參數的誤差方程: BX-L. (27) 按觀測距離定義觀測值的權,并令1 km的觀測高差為單位權,則觀測值的權陣為: P=diag[1/2.0 1/2.0 1/4.0 1/2.0 1/2.0 1/4.0 1/4.0]. (28) 根據最小二乘原理,解算得: (29) 方法二:用約束秩虧間接平差模型的求逆公式法解算上述平差問題。設A,B,P1,P2,P3點的高程為未知參數,將所有觀測值的改正數表示成未知參數的誤差方程: (30) 未知參數的系數矩陣為列秩虧矩陣。 A,B為已知點,組成約束方程: (31) 按觀測距離定義觀測值的權,并令1 km的觀測高差為單位權,則觀測值的協因數陣為: P=diag[1/2.0 1/2.0 1/4.0 1/2.0 1/2.0 1/4.0 1/4.0]. (32) 根據本文推導的約束秩虧間接平差模型的參數估計式(19)計算得: [x1x2x3x4x5]′= {(N+CTC)-1-(N+CTC)-1CT[C(N+ CTC)CT]-1C(N+CTC)-1}BTPL+ (N+CTC)-1CT[C(N+CTC)CT]-1WX= (33) x3,x4,x5為待求點的高程: 方法三:用約束秩虧間接平差模型的虛擬觀測法解算上述平差問題。設A,B,P1,P2,P3點的高程為未知參數x1,x2,x3,x4,x5,在方法二中約束秩虧間接平差模型基礎上,將約束方程看做虛擬觀測,和秩虧間接平差模型組成新的誤差方程: (34) 按觀測距離定義觀測值的權,并令1 km的觀測高差為單位權,令已知點的權陣為單位權陣,則觀測值和虛擬觀測值的權陣為: P′=diag[1/2.0 1/2.0 1/4.0 1/2.0 1/2.0 1/4.0 1/4.0 1 1]. (35) 新誤差方程和原約束方程根據約束間接平差模型的參數估計式,計算得: [x1x2x3x4x5]′= {(B′TP′B′)-1-(B′TP′B′)-1CT[C(B′TP′B′)-1× CT]-1C(B′TP′B′)-1}B′TP′L′+(B′TP′B′)-1CT× [C(B′TP′B′)-1CT]-1WX= (36) 從上述計算過程和結果可見: 1)約束秩虧間接平差模型的求逆式法、虛擬觀測法和間接平差模型對未知點P1,P2,P3的參數估計[x3x4x5]的結果完全一樣,證明本文推導的求逆公式和提出的虛擬觀測算法是正確的。 2)間接平差模型為平差計算最常用的方法,其數學模型和計算比較簡單,但是未區分平差系統的觀測數據和基準數據兩類不同性質的數據。約束秩虧間接平差模型區分了觀測數據和基準數據,約束方程為平差系統提供參考基準,在研究觀測值的內部符合精度、基準數據對參數的影響、基準數據的兼容性等方面具有明顯優勢。 3)虛擬觀測法的約束方程作為誤差方程加入到秩虧間接平差模型中,消除了秩虧間接平差模型的法方程系數矩陣的秩虧,從而將約束秩虧間接平差模型轉換為約束間接平差模型,達到方便計算目的。 在解算約束秩虧間接平差模型時,對參數估計值進行修正和對秩虧間接平差模型的法方程系數進行修正的計算方法比較復雜,應用虛擬觀測值算法為約束秩虧間接平差模型的算法提供了一條新的思路和方法。通過將約束條件看做虛擬觀測,和原有的秩虧間接平差模型組合成新的誤差方程,再和約束條件組成約束間接平差模型進行解算,從而在形式上消除了秩虧間接平差模型的法方程系數矩陣的秩虧,這樣可以采用分塊矩陣求凱利逆的方法求得參數估計。該方法和本文算法的計算結果是一樣的,為解算約束秩虧間接平差模型的提供了一條簡單精確的算法。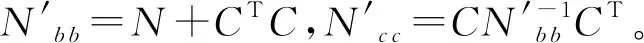
2 約束秩虧間接平差模型的虛擬觀測法
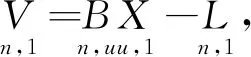
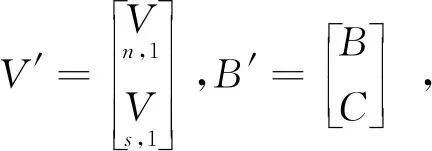
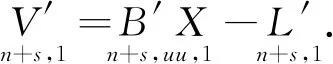
3 案例與分析

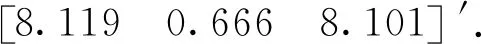
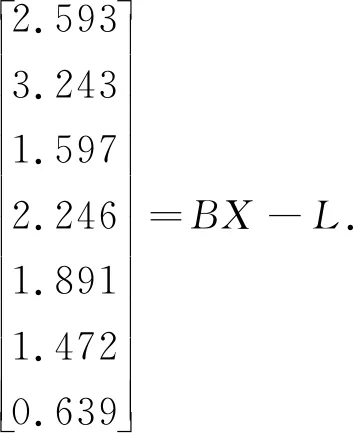
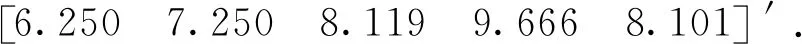
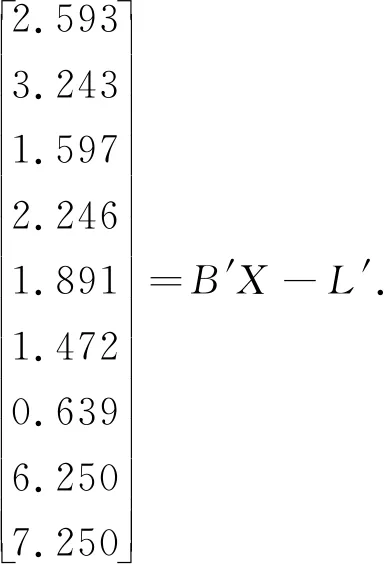
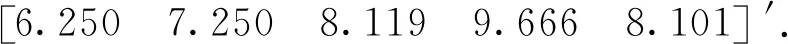
4 結束語

