新型磁集成改進型Cuk變換器

周 立， 李 杰， 孫瑄瑨， 李冠宇

(1.遼寧工程技術大學 電氣與控制工程學院，遼寧 葫蘆島 125105； 2.國網遼寧省電力有限公司錦州供電公司，遼寧 錦州 121000)

為了適應新能源并網發電環境，高性能的DC-DC變換器變得越來越重要。升壓變換器可以在高占空比下工作，以實現更高的電壓增益[1-2]。但在實際應用中，由于受到電源開關、整流二極管以及電路拓撲運行在高頻率情況下等效串聯電容和電阻的影響，使變換器的升壓能力受到了限制，而且較高的占空比會導致變換器的輸出不穩定。

近些年，學者們提出了許多新的拓撲結構，在不使用更高占空比的情況下實現更高的電壓增益[3-6]，文獻[7]和文獻[8]提出了一種基于開關電感和開關電容的升壓單元，可實現較高的電壓增益，但其電感較多體積較大，電路復雜，電流紋波較大，不利于改善變換器的功率密度。文獻[9]通過帶有自舉電容的開關電感單元替代傳統Cuk變換器中的輸入電感，實現了較高的電壓增益，但其結構復雜且在自舉電容儲能時會存在較大的沖擊電流，輸入電流紋波較大。文獻[10]提出了一種基于開關電感和開關電容組合的新型高增益Cuk變換器，能實現較高的電壓增益，但由于前級開關電感的存在，雖提升了變換器電壓增益，但其輸入電流紋波依舊較大。文獻[11]將磁集成技術和交錯并聯技術應用到傳統的Cuk變換中，提出了交錯并聯磁集成開關電感/開關電容Cuk變換器的拓撲，實現了較高的電壓增益輸出和較低的電流紋波，但其所用的器件較多，增加了變換器的成本和功率密度。

本文在傳統Cuk變換器的基礎上，提出一種新型磁集成改進型Cuk變換器，保持傳統的Cuk變換器具有連續輸入和輸出電流的優點，實現了較高的電壓增益，通過磁集成的方式，有效減小了變換器的電流紋波，分析了變換器的工作原理，給出磁集成設計準則，最后通過搭建仿真模型測試和硬件電路測試，充分證明了本變換電路的正確性。

1 變換器拓撲結構及工作原理

1.1 拓撲結構

圖1為改進前的Cuk變換器電路圖，改進后的新型Cuk變換器如圖2所示，增加了2個二極管、1個電感和1個電容元件，設L1=L2=L3=L，電感L2和L3之間的互感為M1，電感L1與電感L2和L3之間的互感均為M2，變換器中的各個器件均為理想元件且電容值足夠大，開關管占空比為D。

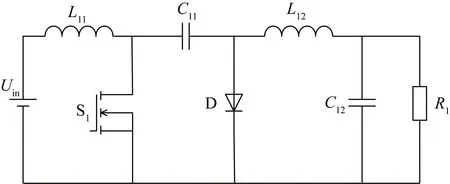
圖1 基本Cuk變換器

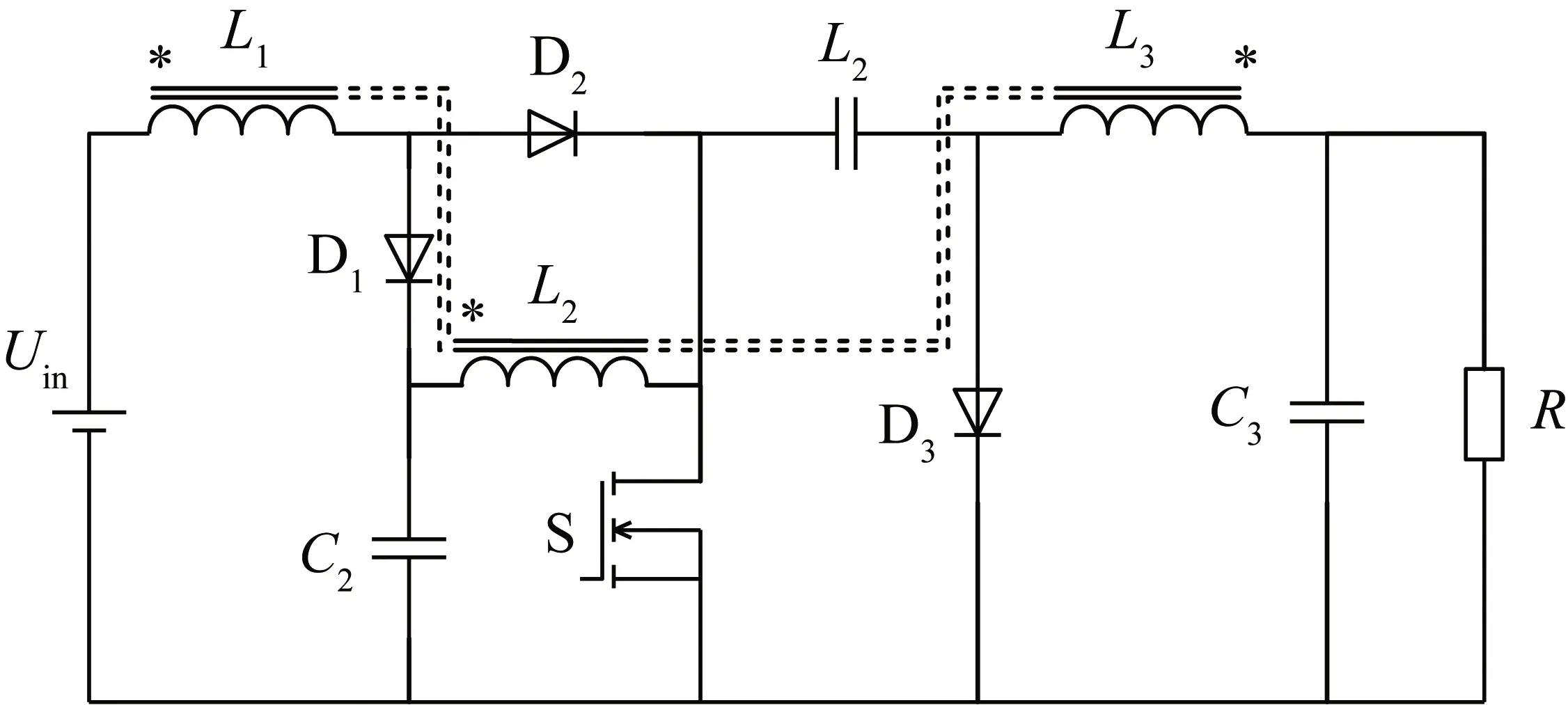
圖2 改進型Cuk變換器

1.2 工作模態分析

改進型Cuk變換器在一個工作周期里存在兩種不同的工作模態，其等效電路及其工作時的輸出特性分別如圖3和圖4所示。

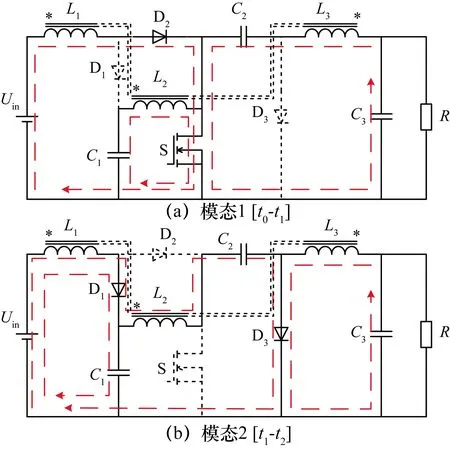
圖3 不同模態等效電路

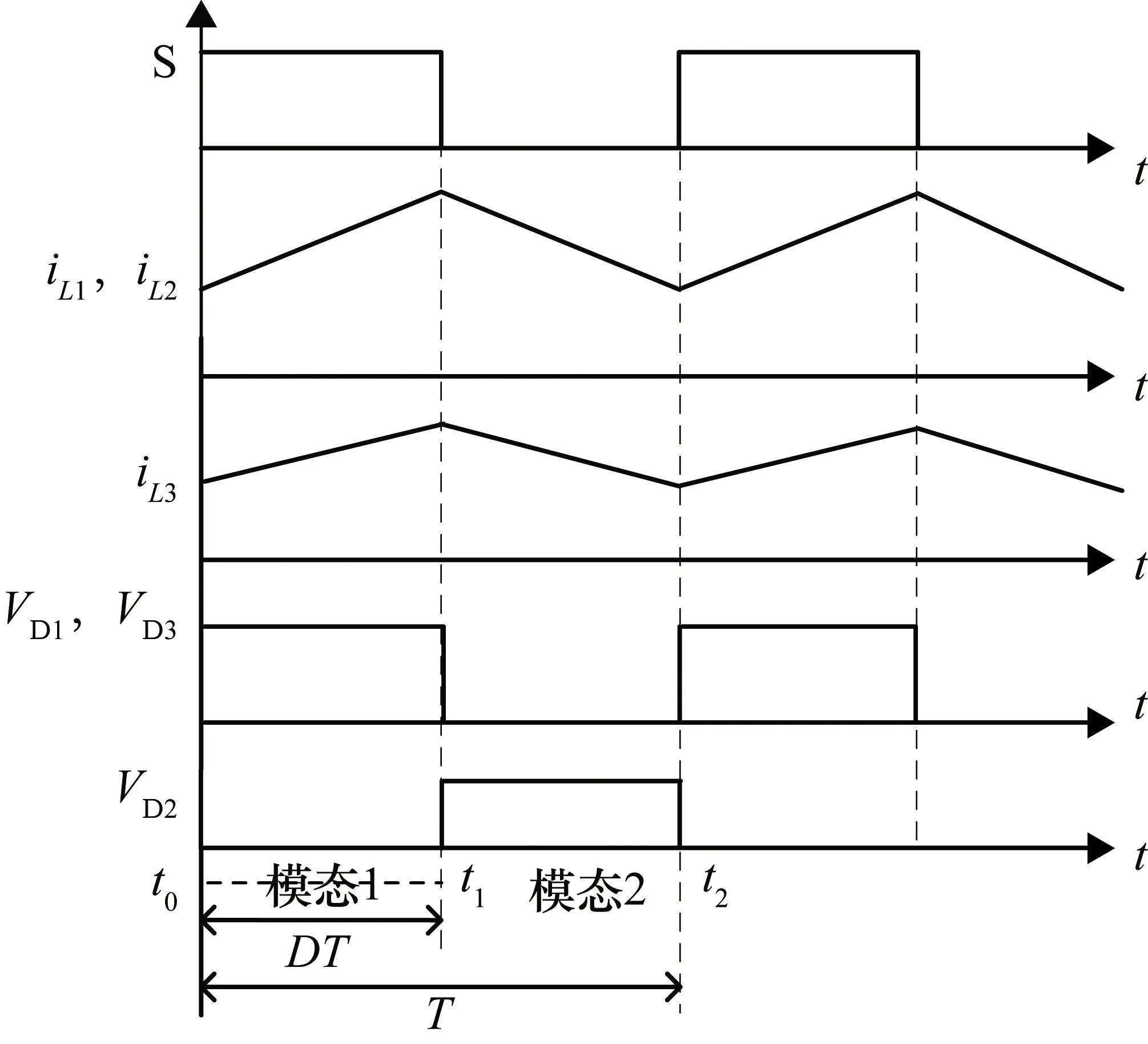
圖4 主要工作波形圖

(1) 模態1[t0-t1]。

模態1[t0-t1]等效電路如圖3(a)所示，開關管S導通，二極管D1和D3反向截止，D2導通，電感L1儲能電感電流iL1線性上升，電容C1經開關管S放電，電感L2儲能電感電流iL2線性上升，電容C2經過開關管向負載和C3放電，電感L3儲能電感電流iL3線性上升，模態方程為

(1)

(2) 模態2[t1-t2]。

模態2[t1-t2]等效電路如圖3(b)所示，開關管S關斷，二極管D1和D3導通，D2反向截至，電源與電感L1串聯經過D1給電容C1充電，電源和電感L1與電感L2串聯給電容C2充電，電感L3經D3向負載供電，模態方程為

(2)

2 變換器性能分析

2.1 電壓增益分析

通過對變換器2個工作模態的分析，可以得出電感電流的變化量：

(3)

(4)

(5)

根據伏秒面積平衡定理[12]，由式(3)～式(5)得出變換器的電壓增益為

(6)

式(6)表明改進型Cuk變換器的電壓增益是傳統Cuk變換器的1/(1-D)倍。

2.2 電壓應力分析

由模態1和模態2可知，電容C1、C2、C3的電壓表達式為

(7)

(8)

uvpsC3=Uo

(9)

變換器工作在模態2時開關管S關斷，開關管兩端承受的電壓等于電容C2兩端的電壓，即

(10)

當開關管S導通時，D1、D3反向截止，二極管D1兩端承受的電壓應力為L2兩端的電壓，L2兩端的電壓等于UC1，即

(11)

二極管D3兩端承受的電壓應力為UC2，即

(12)

當開關管S關斷時，二極管D2兩端承受的電壓應力為

uvpsD2=UC2-UC1=Uo

(13)

2.3 電流紋波分析與耦合度設計準則

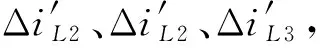
(14)

(15)

(16)

(17)

(18)

式中，ε1、ε2為電感集成前后電流紋波系數，由式(18)和式(19)可知，ε1、ε2不僅與耦合系數k1、k2有關，還與占空比D有關。以D=0.5為例(右端垂直線為分母為0的無意義情況)，紋波系數ε1、ε2與k1、k2關系圖如圖5所示。在不同占空比的情況下，ε1、ε2的變化規律如虛線箭頭所示，以紋波系數ε1為例，當占空比D增加時，曲線沿著箭頭方向收縮，當D減小的時候，曲線沿箭頭方向伸展。

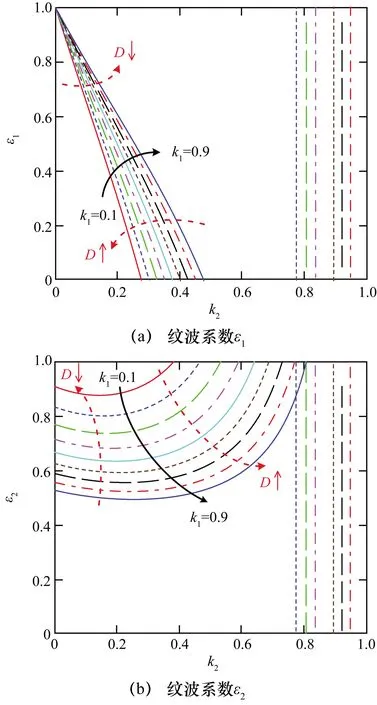
圖5 電感電流紋波系數與耦合度關系圖

在圖5中，實線箭頭所示的方向為k1由0.1增加到0.9的曲線。根據圖5(b)可知，當k1越大，ε2越小，即當k1趨近于1為全耦合的時候，電感L2、L3中的紋波減小得越多，而當k2越大時，ε2先減小后增大。再結合圖5(a)可知，當k2越大，ε1越小直至減小到0。故可選擇一個合適的k2值，使得ε1和ε2都減小。在D=0.5時，取k2為0.4左右的時候，ε1減小得非常多，同時ε2也減到最小。在實際應用中，可使k1均趨近于1為全耦合，根據變換器的參數，設計合適的耦合系數k2，使3個電感中的電流紋波都明顯減小。

2.4 電感磁集成設計

由電感L1、L2、L3的耦合度設計原則可得，由于電感L2、L3為全耦合，因此L1與L2、L3之間的耦合系數需要進行調整，故在本設計中，集成磁件的磁心結構采用“EE”型，該結構左右對稱，電感L2、L3繞在一個側柱上，另一個電感L1繞在另一個側柱上，如圖6所示。通過不斷調整磁芯中柱氣隙就可以有效調整L1與L2、L3的耦合系數k2，集成磁件等效磁路與簡化磁路如圖7所示。

圖6 “EE”型磁心結構圖

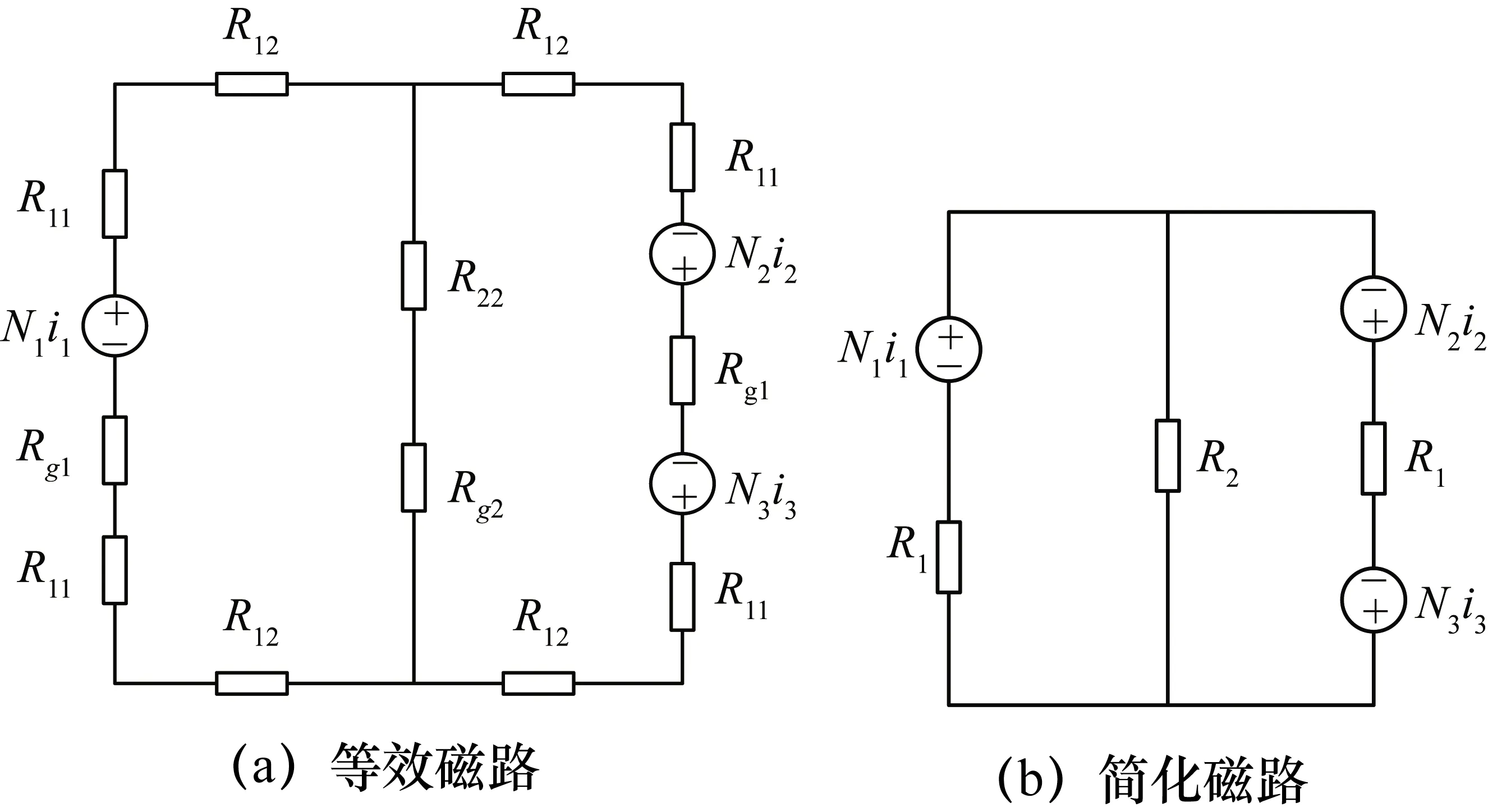
圖7 集成磁件等效磁路與簡化磁路

由于磁件為左右對稱結構，因此該結構對應的磁路阻抗如圖7(a)所示，其中左右柱和中柱磁路上的磁阻分別設為R11，R12，R22，左右柱氣隙對應的磁阻設為Rg1、中柱氣隙對應的磁阻設為Rg2。將3條磁路的磁阻進行等效簡化，其簡化磁路如圖7(b)所示，且滿足：

(19)

在簡化磁路的基礎上，進行對偶和尺度變換[14]得到磁路的等效電路如圖8(c)所示。

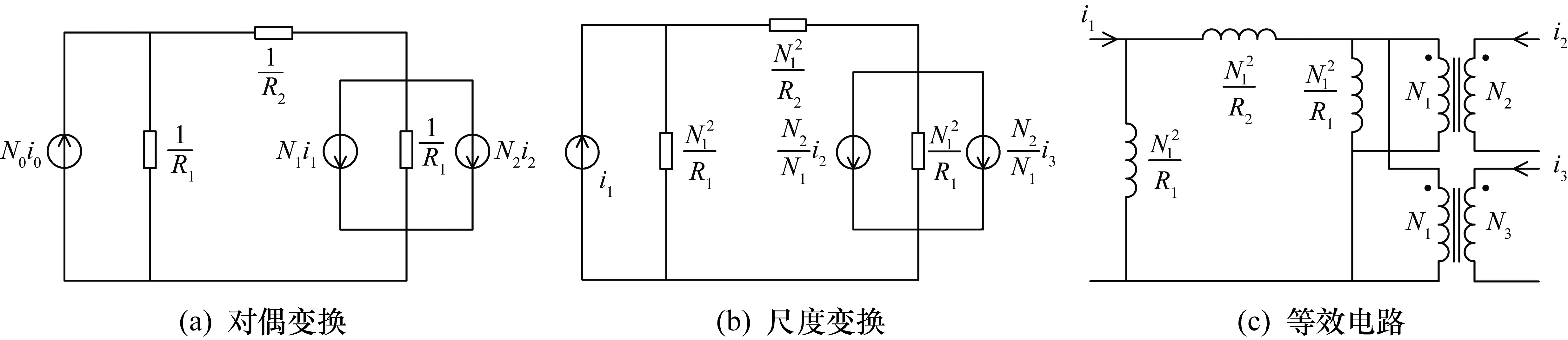
圖8 等效電路圖

根據圖8可知，在忽略漏感的情況下，根據電感和磁阻之間的關系可得到3個電感繞組L1，L2，L3的自感以及電感繞組之間的互感與相應磁阻的關系：

(20)

式中，M1為電感L2與L3的互感值；M2為電感L1與L2(L3)的互感值。由式(20)可得耦合系數k1，k2的值為

(21)

由式(21)可知，耦合系數k1的大小為固定系數1，耦合系數k2的大小隨著磁阻R1和磁阻R2的變化而變化，因此當磁阻R1固定不變時，可以通過調節中柱磁阻R2的大小來不斷調整耦合系數k2的大小，且耦合系k2隨著中柱磁阻R2增大而增大。在實際設計中，根據變換器的參數，設計出合適的耦合系數k2，再通過調節中柱磁阻R2的大小，進而調節k2的大小以符合設計要求，且將3個電感集成到一個磁件上以減小磁件體積。

3 仿真與實驗驗證

3.1 仿真驗證

進行仿真驗證時設置的參數具體如下：輸入電壓Uin=12 V；開關頻率fs=50 kHz；占空比D=0.5；負載R=20 Ω；電感L1=L2=L3=70 μH；耦合系數k1=0.9，k2=0.4；電容C1=C2=47 μF，C3=100 μF。經仿真，輸出電壓波形圖如圖9所示，電感L1和電感L2、L3的電流紋波圖如圖10和圖11所示。電感集成后，電感L1電流紋波由1.64 A減小到0.31 A，耦合后電流紋波近似為未耦合紋波的19%，理論計算得ε1=0.18987近似等于仿真的值；電感L2、L3電流紋波由3.38 A減小到1.74 A，耦合后電流紋波為非耦合紋波的51%，理論計算得ε2=0.5063近似等于仿真的值，驗證了理論的正確性。

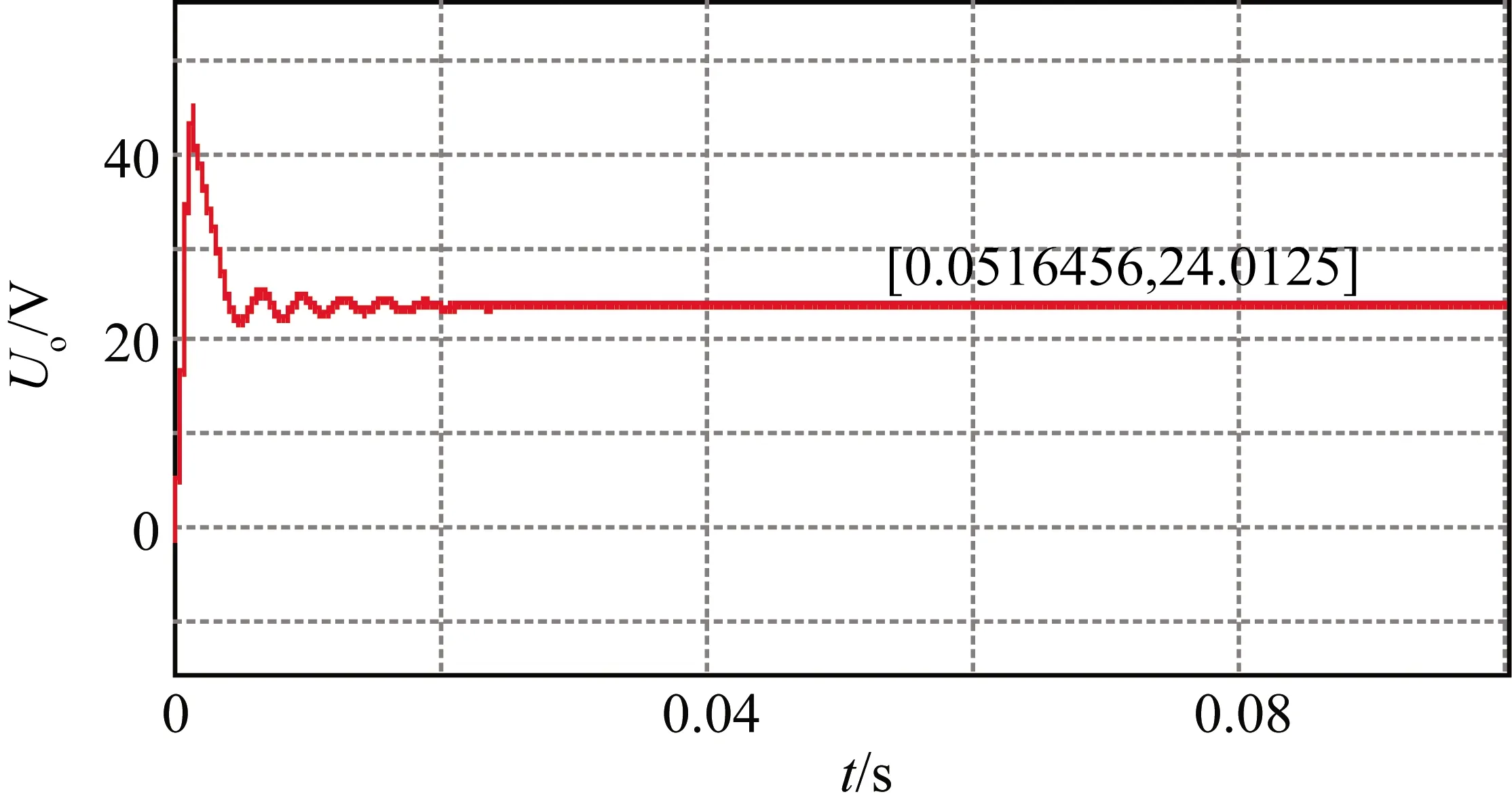
圖9 輸出電壓波形

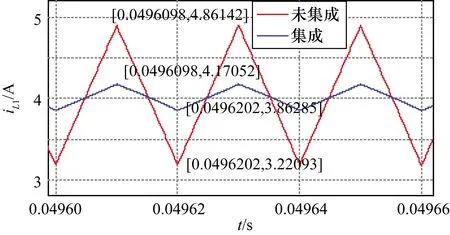
圖10 電感L1電流紋波

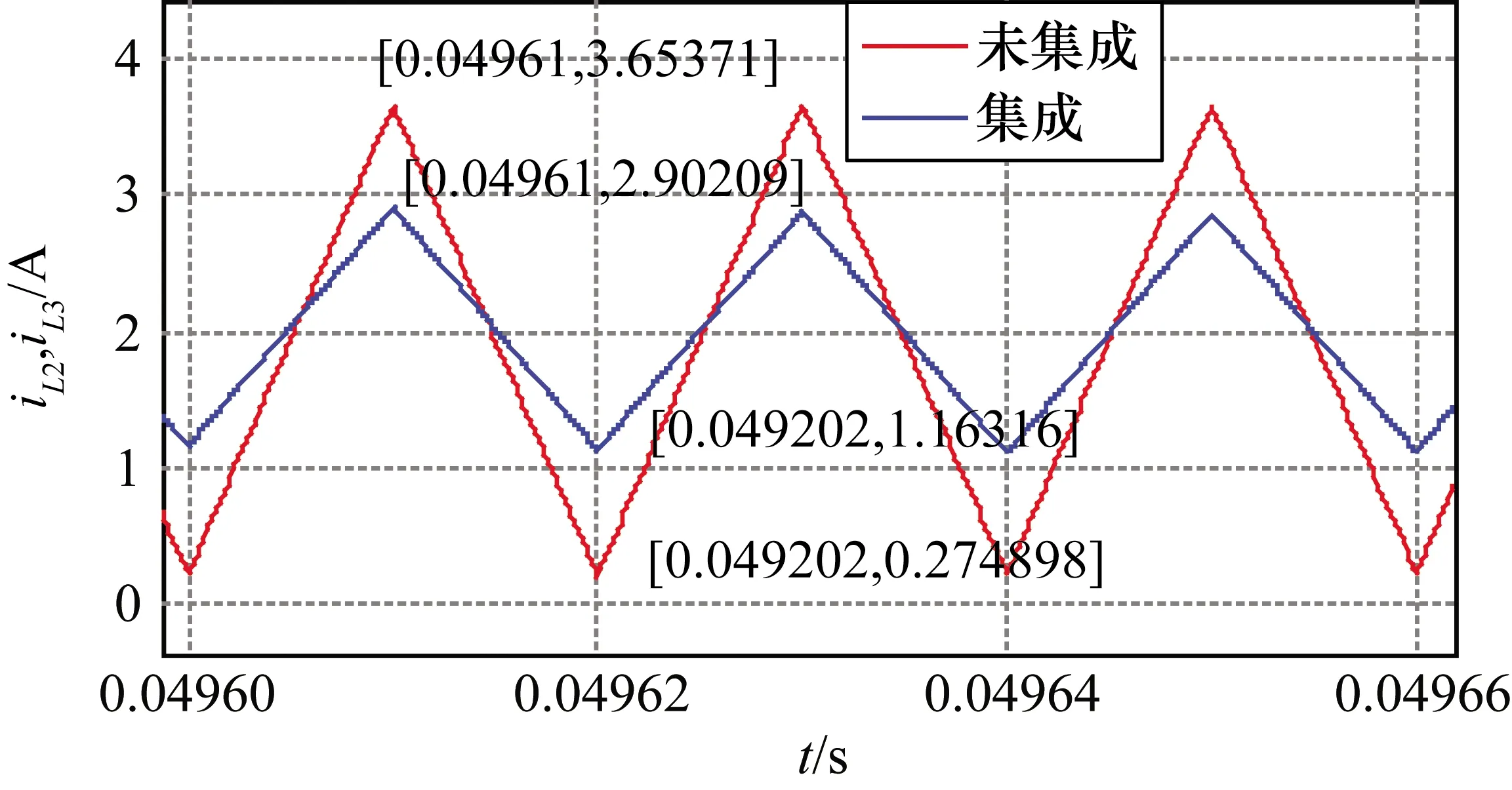
圖11 電感L2、L3電流紋波

3.2 實驗驗證

磁集成改進型Cuk變換器樣機參數與仿真參數設置相同，集成磁件電感參數如表1所示。

表1 集成磁件電感參數 單位：μH

變換器輸入輸出電壓實驗波形如圖12所示，輸出電壓約為24 V，驗證了變換器設計的正確性。電感L1、L2、L3的電流紋波波形如圖13所示，電感電流測量采用ETA5301A電流探測鉗進行測量，單位為100 mV/A。在電感未集成情況下，電感L1的電流紋波約為1.7 A，電感L2(L3)的電流紋波約為3.4 A；在對電感集成后，電感L1的電流紋波約為0.3 A，電感L2(L3)的電流紋波約為1.9 A；與仿真分析基本一致，驗證了理論正確性。變換器效率曲線如圖14所示。

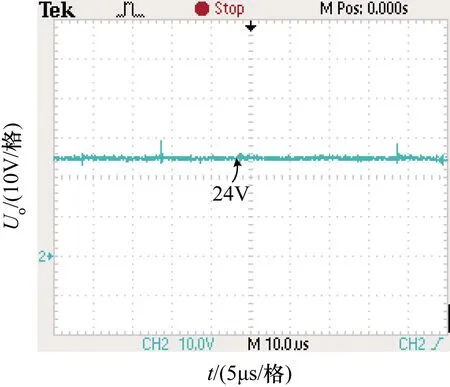
圖12 輸出電壓實驗波形圖

圖13 磁集成電流紋波實驗波形圖

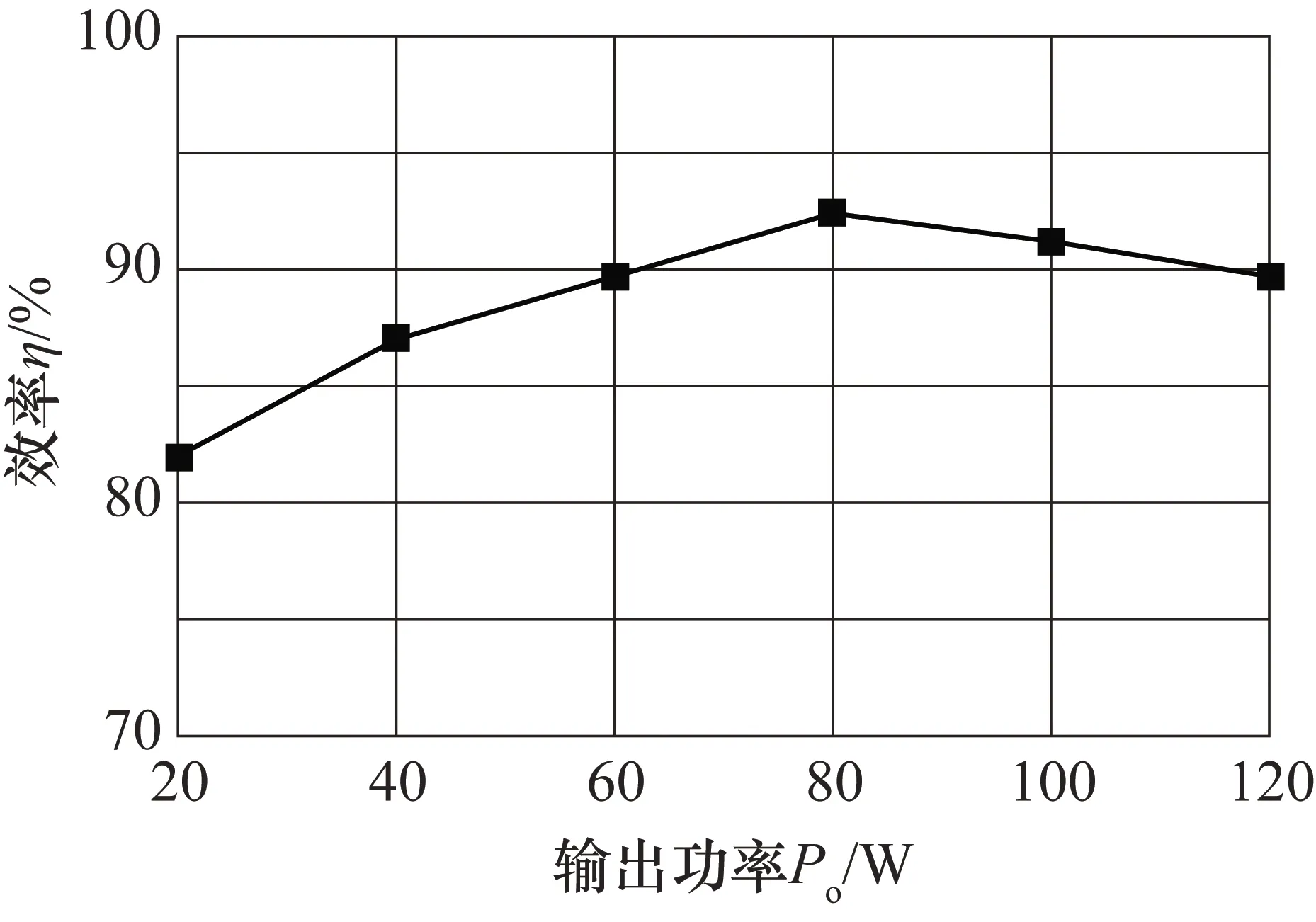
圖14 變換器效率曲線

4 結論

提出了一種新型磁集成改進型Cuk變換器，推導出了變換器的電壓增益、開關器件的電壓應力和電流紋波的表達式，給出了電感耦合度設計準則和磁件設計方案，改進型Cuk變換器具有以下優點：

① 本設計中的新型Cuk電路結構簡單；

② 相對于傳統Cuk電路而言，本設計中的新型Cuk電路擁有更大的電壓增益，其值是傳統Cuk變換器的1/(1-D)倍；

③ 相對于傳統Cuk而言，本Cuk變換器在電感磁集成后變換器磁性器件的體積將變得更小且具有更小的輸入輸出電感電流紋波。

綜合上述優點該變換器具有良好的整體性能。