從特殊到一般的學習方法

段劉宇

在“平面圖形的認識（二）”中，我們用從特殊到一般的方法，依據“三角形的內角和是180°”得出多邊形內角和的一般結論：180°?（n-2）（其中n為多邊形的邊數）。教材上是從四邊形開始，通過添加輔助線，把四邊形分成2個三角形，把五邊形分成3個三角形，把六邊形分成4個三角形……然后一般化，把n邊形分成（n-2）個三角形，最終獲得結論（當然分割轉化的方法不唯一）。

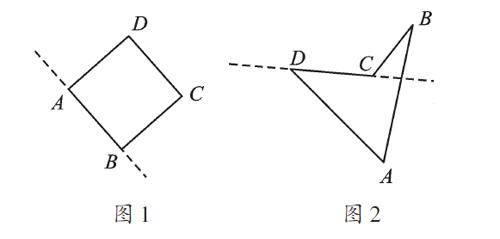
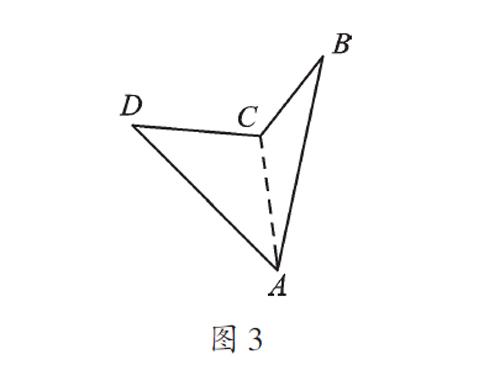
教材上研究的都是凸多邊形。凸多邊形指如果把多邊形的任意一條邊向兩方無限延長成為一直線時，其他各邊都在此直線的同一旁的多邊形。凸多邊形的內角沒有一個是優角（大于180°且小于360°的角），如圖1。凹多邊形指把一個多邊形的某條邊向兩方無限延長成為一直線時，其他各邊不全在此直線的同一旁的多邊形。凹多邊形的內角中至少有一個優角，如圖2。凹多邊形的內角和也是一樣的結論嗎？

我們可以先回顧一下探究凸多邊形內角和的方法，然后將同樣的辦法遷移到探究凹多邊形的內角和中。

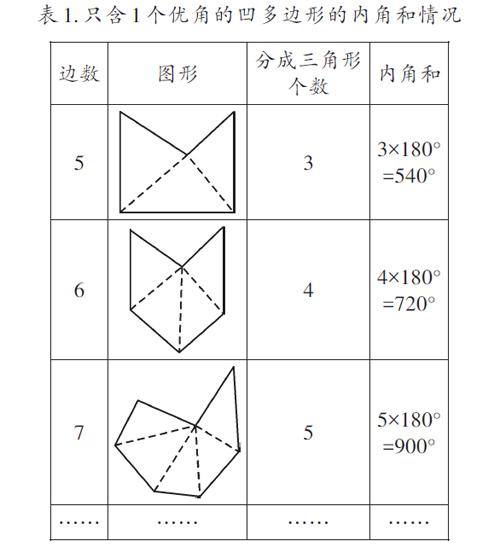
以凹四邊形為例，如圖3。連接點A和點C，線段AC把這個凹四邊形分為兩個三角形，這兩個三角形的內角和就是這個凹四邊形的內角和，即2×180°=360°。看到這個結果，我們不由自主地猜想：凹多邊形的內角和公式會不會跟凸多邊形的內角和公式一樣呢？多舉幾個例子，如表1。

這樣，我們就更有理由歸納一般性規律，即凹n邊形內角和為180°?（n-2）（其中n為多邊形的邊數），這與凸n邊形的結論一樣。

但這仍然是片面的，如果凹多邊形包含兩個及以上優角，該結論還能不能成立呢？不妨以包含兩個優角的凹多邊形為例，如表2。

我們仍然可以類似地去考慮含3個優角（從凹八邊形開始）的凹多邊形，特殊的例子越充分、越全面，我們就越有信心確信凹n邊形內角和的結論。

因此，不論是凸多形還是凹多邊形，可以得到一個關于多邊形內角和的通用公式，即n邊形的內角和為180°?（n-2）（其中n為多邊形的邊數）。

這是一個多么簡潔美妙的結論啊！小伙伴們，從特殊到一般，這是我們在看教材、學新知的時候，經常碰到的方法。特殊的例子中蘊含著一般的規律，一般的規律可以用特殊的例子驗證。當我們運用這種方法遷移運用、研究問題的時候，就能體驗到發現的樂趣，體會到結論的美妙，領悟到方法的神奇。同學們，在遇到具有一般性的問題時，試著用特殊到一般的方法大膽探索吧。

教師點評

學習數學不僅僅是記住結論，更應該掌握數學結論形成的過程及其蘊含的數學思想方法，更包含在過程中所感受到的積極情感、數學之美和嚴謹求證的價值觀念等。小作者不僅能夠學好多邊形內角和的結論，還能夠把結論形成過程中的方法遷移到更全面的多邊形的不同類別中，最終形成了更全面的認識。在這個過程中，他不僅學會了知識，更掌握了方法，還領悟了特殊與一般的關系，獲得了美好的體驗，產生了對數學學習的積極的興趣。他的這種學習方法，值得同學們借鑒。

（指導教師：鐘 鳴）