基于連續介質損傷力學的坑蝕鋼筋高周疲勞壽命與損傷分析

張 昉, 金偉良, 張 軍, 毛江鴻, 樊瑋潔

(1.浙江大學 結構工程研究所, 浙江 杭州 310058; 2.浙大寧波理工學院 土木建筑工程學院, 浙江 寧波 315100)

大量沿海鋼筋混凝土橋梁在服役過程中同時遭受氯鹽侵蝕和車輛反復荷載作用.氯鹽侵蝕下鋼筋銹蝕形態多為坑蝕[1],造成鋼筋截面積減小和應力集中,在反復荷載作用下極易發生疲勞斷裂[2],嚴重降低鋼筋混凝土結構的服役壽命[3].

S-N曲線法是預測銹蝕鋼筋疲勞壽命的重要方法.已有研究[4-5]表明,在雙對數坐標下,銹蝕鋼筋的疲勞壽命和應力幅值仍然為線性關系,并建立了考慮銹蝕率的銹蝕鋼筋的S-N曲線方程.該方法需要大量的疲勞試驗,只關注疲勞壽命而忽略了疲勞損傷的非線性發展過程,也無法探明鋼筋銹蝕對其疲勞性能的影響機理.此外,斷裂力學(FM)可以很好地描述疲勞裂紋擴展行為,并預測疲勞壽命,如衛軍等[6]研究了半橢圓形蝕坑鋼筋裂紋擴展規律;Sun等[7]建立了最大蝕坑深度和銹蝕率的關系式,定義等效初始裂紋尺寸以提高構件疲勞壽命的預測精度等.一方面,FM法適用于單個裂紋占主導的情況,往往還需要對不規則蝕坑缺陷做簡化等效處理[8],難以考慮鋼筋多蝕坑之間的互相影響.另一方面,FM法主要研究疲勞裂紋擴展計算方法,無法給出疲勞損傷累積和局部應力場的演化.

基于熱力學理論,連續介質損傷力學(CDM)通過定義損傷變量來研究反復荷載作用下材料力學性能退化規律和機理[9],能夠描述宏觀疲勞裂紋擴展前,材料內部的損傷演化過程,如Zhang等[10]通過三維有限元法實現了CDM多軸疲勞損傷理論在鈦合金中的應用,并驗證了其在微動疲勞研究中的有效性;Do等[11]基于CDM疲勞模型和有限元法,考慮殘余應力的影響精確預測了對接焊縫高周疲勞壽命.CDM方法可用于研究構件表觀形貌對疲勞損傷非線性發展的影響,非常適合實際工程中具有復雜表面特征的銹蝕鋼筋的疲勞研究,可以彌補傳統疲勞研究方法的諸多不足,但目前鮮有文獻關注到CDM模型在坑蝕鋼筋高周疲勞分析中的應用.

本文首先引入基于CDM的疲勞損傷模型,然后通過鋼筋試件疲勞試驗獲取模型參數,利用Abaqus用戶自定義材料子程序(Umat)編寫算法程序,基于加速銹蝕鋼筋的蝕坑尺寸建立有限元模型,最后結合坑蝕鋼筋疲勞試驗進行疲勞壽命預測及疲勞損傷和應力場演化的分析.可以為非均勻銹蝕形態下的鋼筋疲勞損傷研究提供參考.

1 連續介質損傷力學模型

循環載荷作用下,各向同性材料的力學性質劣化表現為剛度的下降.定義損傷變量(D)為[9]：

(1)

式中：E為無損傷材料的彈性模量,MPa;ED為有損傷時的等效彈性模量,MPa;D的變化范圍為0～1.

根據應變等效原理,耦合損傷的彈性本構關系為：

(2)

式中：v是材料的泊松比;σij和εij分別是應力張量和應變張量;σkk是第一應力不變量；δij是Kronecker符號.

對于高周疲勞,損傷演化法則依賴于循環荷載作用下材料的應力狀態和循環次數.Chaudonneret[12]提出了一種適用于多軸應力狀態的疲勞損傷演化模型：

(3)

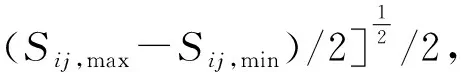
2 疲勞試驗

GB 50010—2010《混凝土結構設計規范》推薦使用HRB400鋼筋,但目前尚未檢索到相關文獻中有提出HRB400鋼筋材料的CDM模型參數.本文開展HRB400鋼筋材料性能試驗以獲取模型參數,并進行坑蝕鋼筋的高周疲勞試驗,用以驗證本文基于CDM理論的鋼筋疲勞有限元模擬.

2.1 參數標定試驗

試件由直徑20mm的HRB400鋼筋加工而成,其化學組成見表1,幾何尺寸見圖1.

表1 HRB400鋼筋化學組成

圖1 試件尺寸Fig.1 Specimen size(size:mm)

先通過靜態拉伸試驗獲得試件的極限抗拉強度(σu).3個試件的σu實測值分別為581、586、585MPa,平均值為584MPa.疲勞試驗采用長春機械院生產的25t電液伺服疲勞試驗機,加載模式采用應力控制的軸向常幅循環加載,加載頻率取5Hz.試驗分組、加載參數及試件疲勞壽命見表2.其中σmax為最大拉伸應力,σm為平均拉伸應力,Nf為疲勞壽命,Nfm為平均疲勞壽命.

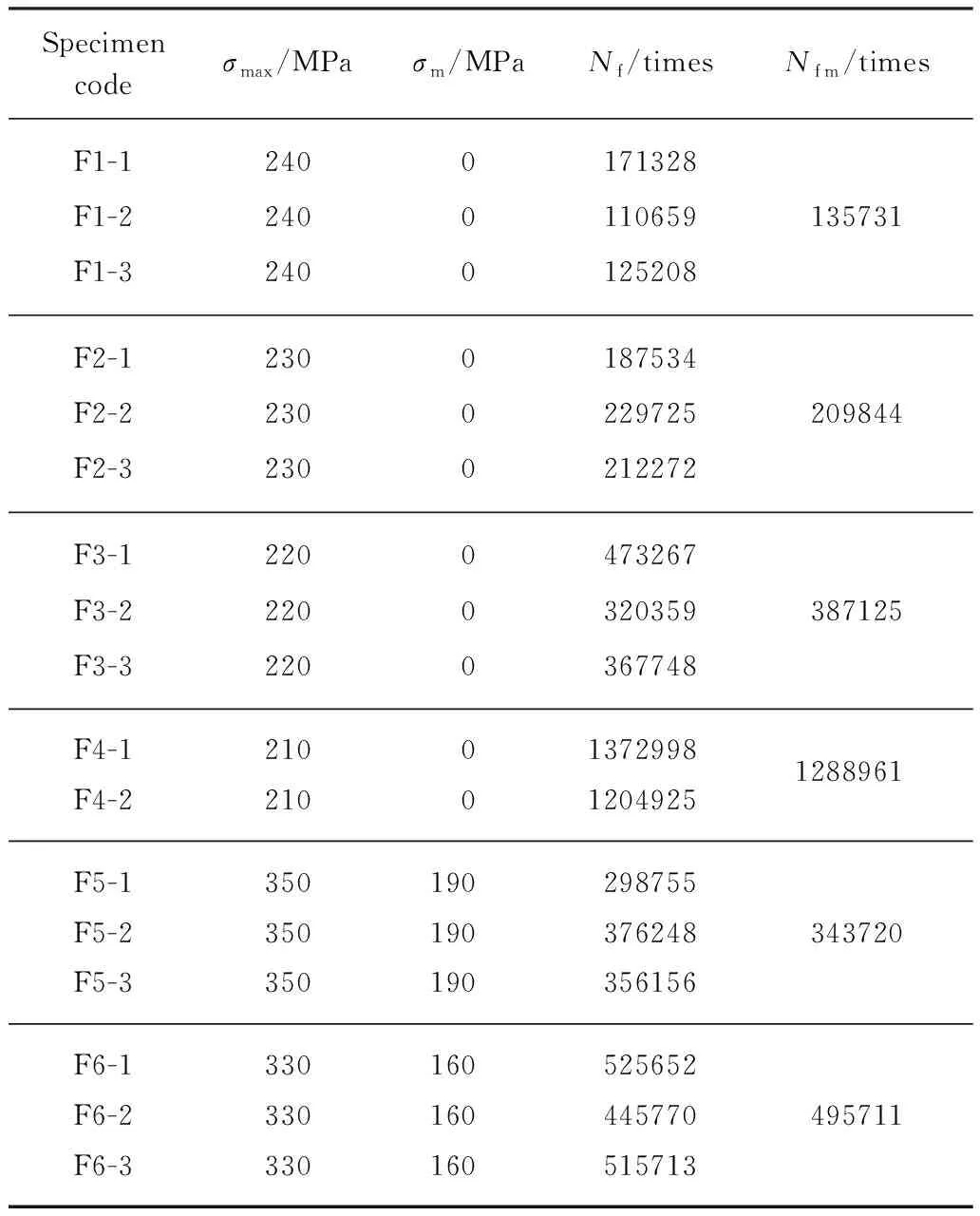
表2 HRB400鋼筋試件疲勞試驗結果

2.2 坑蝕鋼筋高周疲勞試驗

采用2.1節所述的鋼筋試件,通過外加電流加速

銹蝕的方法制作鋼筋蝕坑：先在試件表面緊密纏繞防水絕緣膠帶,并在居中位置制作1個橢圓孔,兩端用硅酮膠密封防水(見圖2);將浸入5%(質量分數)NaCl溶液中的試件作為陽極,不銹鋼片作為陰極,連接至直流電源(見圖3),電流密度控制為400μA/cm2;通過控制初始橢圓尺寸與通電時間,可以獲取不同蝕坑尺寸的銹蝕鋼筋試件.

圖2 預處理的鋼筋試件Fig.2 Pretreated steel bar specimen

圖3 加速銹蝕裝置Fig.3 Accelerated corrosion setup

通電過程完成后取出試件,用乙酸溶液除去銹蝕產物并用清水洗凈,使用游標卡尺測量蝕坑三維尺寸后放置于干燥的密封盒內.蝕坑接近半橢球形,因此采用半橢球模型描述蝕坑形態,本文鋼筋銹蝕形貌及半橢球模型的幾何參數如圖4所示.坑蝕鋼筋試件高周疲勞試驗的試驗設計同2.1節,蝕坑尺寸、加載參數及疲勞壽命見表3.

圖4 銹蝕鋼筋試件Fig.4 Corroded steel bar specimen

表3 銹蝕鋼筋試件的蝕坑尺寸與疲勞試驗結果

3 有限元模擬

3.1 材料參數

材料極限抗拉強度取實測均值σu=584MPa,楊氏模量E取210GPa,泊松比v為0.3[13].根據Basquin公式[14]外推的方法,計算鋼筋在應力比R=-1情況下的疲勞極限σ10.Basquin公式的對數形式為：

lgNf=Algσa+B

(4)

式中：σa是應力幅值,MPa;σa=σmax-σm,A和B是無量綱材料參數.

根據式(4),對表2中F1～F4組的數據進行線性擬合,得lgNf=-16.62 lgσa+44.61.取應力循環基數為2×106次,即可得到σ10=205MPa.

在疲勞損傷演化法則中,有β、M0、a、b1和b2共5個參數待標定.將損傷演化方程(3)以單軸應力形式[10]積分,得到光滑試件在常幅疲勞荷載作用下的疲勞壽命表達式：

(5)

用表2中F1～F4的試驗數據點可擬合得β、aM0-β的值.將F5和F6的試驗數據代入式(5),可得到參數b1和b2的值.對于參數a,采用Zhang等[10]提出的數值方法求解.HRB400鋼筋的CDM疲勞損傷演化模型參數的取值列于表4.

表4 HRB400鋼筋疲勞損傷演化模型的參數取值

3.2 材料子程序算法

由前述模型可知,應力場與損傷場耦合,損傷變量D隨著荷載循環而發生非線性的演化,需應用數值算法求解.本文利用Abaqus軟件的Umat模塊,使用Fortran語言定義材料屬性,用于有限元法分析.算法流程圖見圖5,具體步驟為：

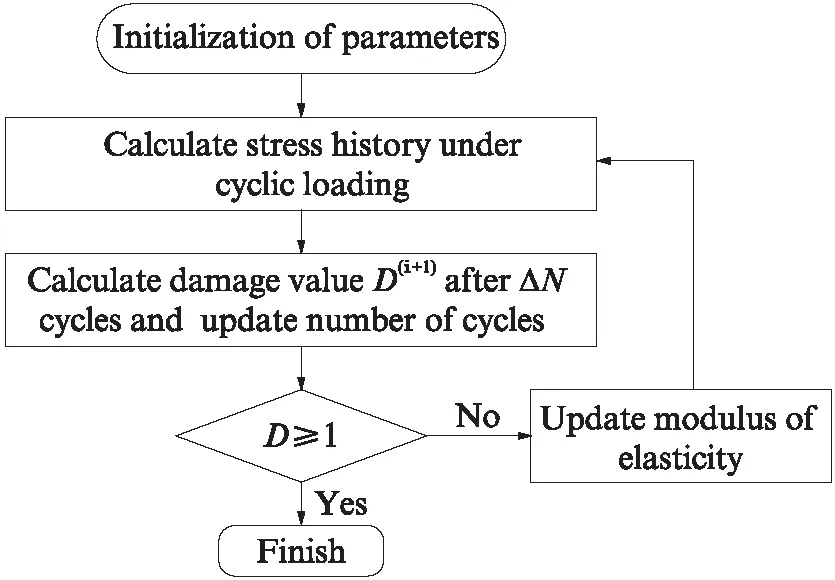
圖5 算法流程圖Fig.5 Flowchart of the numerical algorithm

(1)初始化材料參數.將損傷初始值設定為0.

(2)調用Abaqus求解器,求解耦合損傷的彈性本構關系式(2),計算出該次循環荷載下每個積分點的應力歷程.

(3)計算損傷值,更新循環次數.由于高周疲勞的壽命值較大,若逐次計算所有循環過程,將耗費大量時間.本文采用跳躍式的算法,即假設在ΔN次循環內,損傷值及應力場不變[15].為了保證計算精度,并且節約計算成本,取ΔN的值為疲勞壽命的1%.通過式(3)計算得到損傷演化率dD/dN,更新損傷累積值為D(i+1)=D(i)+(dD/dN)(i)·ΔN,更新循環次數N(i+1)=N(i)+ΔN.

(4)判斷是否有積分點的損傷值達到1.如有,則結束程序,輸出N(i+1)為疲勞壽命.否則,利用損傷累積值更新材料彈性模量E(i+1)=E(i)·(1-D(i+1)),由此實現材料在循環荷載作用下的力學性能退化,重復步驟(2)、(3),直到有積分點的損傷值達到1.

3.3 有限元模型

根據試件CF1～CF6實測蝕坑尺寸建立有限元實體模型(見圖6),模型僅針對試件的有效測試段,不考慮夾持段與過渡段.以試件CF1為例,圖6(a)為其有限元模型網格劃分,單元類型采用8節點六面體線性實體單元(C3D8).為獲得精確的分析結果,在蝕坑處進行網格細分,如圖6(b)所示,單元尺寸控制在50～80μm.材料屬性調用3.2節所述的Umat子程序.在第1個分析步中施加290MPa的定值軸向均布荷載,在后續分析步中施加最大值為290MPa,應力比0.1的軸向循環應力.其他各試件的有限元模擬過程均類似.

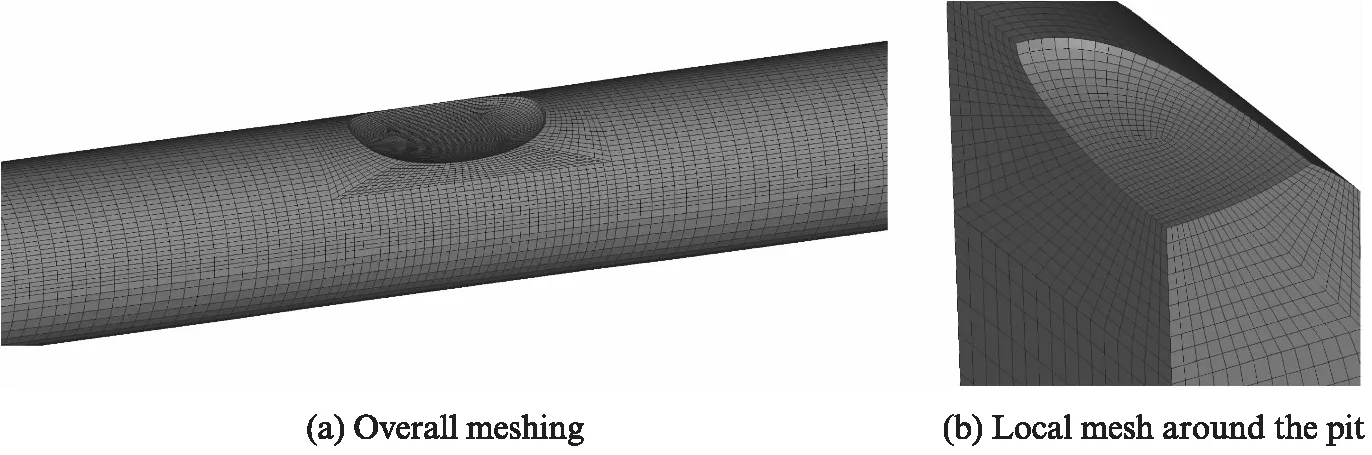
圖6 試件CF1有限元模型網格劃分Fig.6 Mesh of the FE model of specimen CF1

4 試驗與模擬結果分析

4.1 疲勞壽命

將有限元模型提交Abaqus求解器后即可獲得坑蝕鋼筋的疲勞壽命預測值.為驗證本文方法的有效性,收集了王玨[16]與Chen等[17]的試驗數據,對適于彈性疲勞損傷分析的試件進行了數值模擬.若使用傳統的S-N法[4-5,18]預測疲勞壽命,需要得到與本文各試件相同的銹蝕率和應力比試驗數據,且難以考慮蝕坑的影響,故難以進行.因此,本文應用Sun等[7]基于FM法提出的坑蝕鋼筋疲勞壽命計算公式,預測了各試件的疲勞壽命,結果如圖7所示.其中,實心點為本文CDM模型預測壽命與實測壽命的對比,空心點是FM法預測疲勞壽命與實測壽命的對比,實線表示預測值與試驗值相等,虛線表示±0.08的置信區間,相當于約20%(10±0.08)誤差的范圍.

由圖7可見,本文的CDM模型預測坑蝕鋼筋高周疲勞壽命與試驗基本相吻合,也能夠較好地符合文獻[16]的疲勞試驗結果,但與文獻[17]的個別數據有較大偏離,原因可能是試驗用鋼筋性能存在差異.此外,FM方法亦能較好地預測疲勞壽命,但是當應力比不同時,FM法預測值偏差較多,原因是FM模型參數與蝕坑形態、應力比等相關,而本文方法可考慮銹蝕形態和應力狀態的影響,結果也更為準確.由以上分析可知,基于CDM方法預測銹蝕鋼筋的疲勞壽命在不同蝕坑尺寸、不同的應力水平下均有良好的適用性.

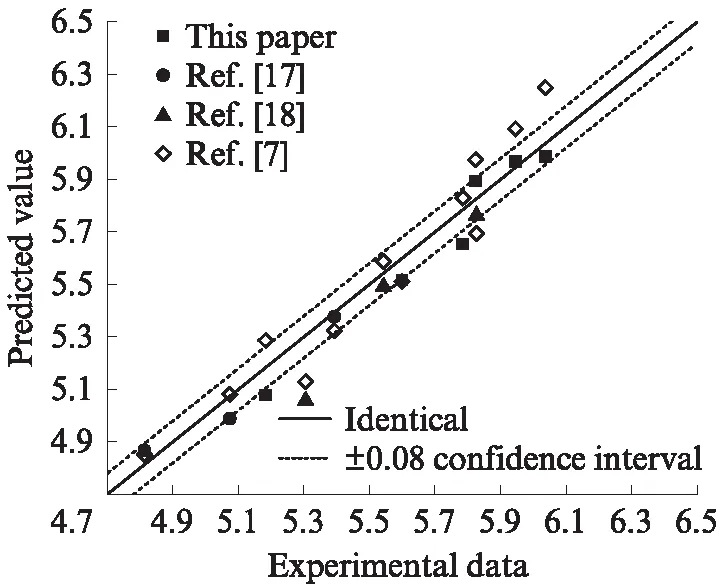
圖7 疲勞壽命預測值與試驗值對比Fig.7 Comparison between the predicted fatigue life and the testing data

4.2 疲勞損傷演化

由于蝕坑處存在應力集中,疲勞損傷集中發生在蝕坑底部.圖8為有限元計算得到的試件CF1蝕坑表面處損傷分布的變化過程.由圖8可見,疲勞前期損傷范圍較小,損傷值也很小,疲勞后期可明顯觀察到疲勞損傷累積,損傷區域從蝕坑底部逐漸向周圍擴展.為了定量研究蝕坑損傷分布,以試件CF4有限元計算結果為例,設定以蝕坑底部為起點,沿鋼筋軸向(x方向)到蝕坑邊沿的路徑,圖9中紅色的節點標記出了該路徑.

圖8 試件CF1有限元模型疲勞損傷分布Fig.8 Distribution of fatigue damage of specimen CF1 FE model

圖9 試件CF4有限元模型路徑的定義Fig.9 Path definition of specimen CF4 FE model

圖10為不同循環次數下,沿試件CF4路徑的損傷值分布.由圖10可見：在疲勞中前期,各點損傷值均很小,僅略微大于0;疲勞后期在蝕坑底部附近損傷發展較快,蝕坑底部的節點損傷值先達到1,而距離2mm 之外的節點疲勞損傷發展較慢.這種現象表明,蝕坑加劇了鋼筋的疲勞損傷,使鋼筋容易形成宏觀疲勞裂紋,降低鋼筋疲勞壽命.這與試驗中鋼筋斷裂位置在蝕坑底部相符.

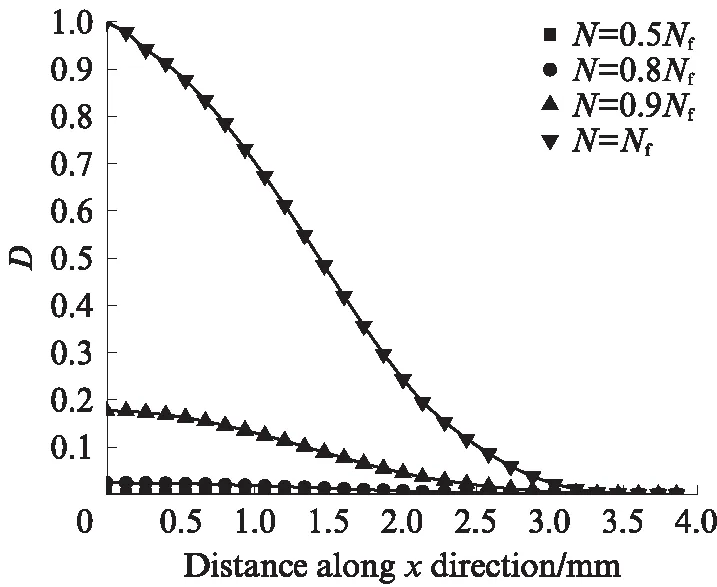
圖10 不同循環次數下沿試件CF4路徑的損傷分布Fig.10 Distribution of damage along the path of specimen CF4 at different number of cycles

提取試件CF1～CF6蝕坑底部處的損傷值隨循環次數N的變化,獲取其疲勞損傷演化,如圖11所示.由圖11可見,各試件在疲勞初期的損傷值較低,當循環次數接近疲勞壽命時,疲勞損傷迅速累積,CDM模型的疲勞損傷累積規律是非線性的.

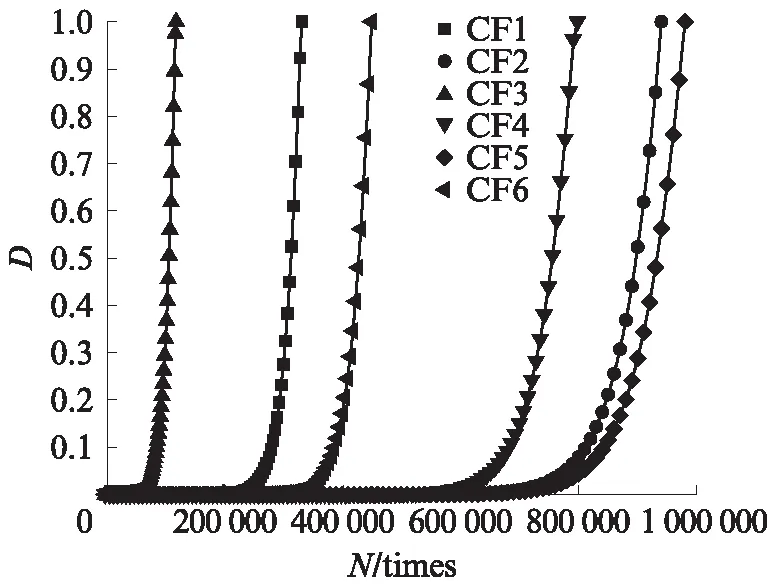
圖11 試件CF1～CF6 蝕坑底部的疲勞損傷演化Fig.11 Damage evolution at the bottom of pits of specimen CF1-CF6

4.3 應力場演化

圖12為試件CF2在疲勞初期與中后期1次循環中Mises應力最大值(σeq,max)的分布.由圖12可見,在疲勞初期,蝕坑部位存在明顯的應力集中,由4.2節可知,該處損傷發展也較為集中.因為材料彈性模量隨著損傷的累積而逐漸降低,在疲勞后期蝕坑內σeq,max卸載到較低值,如圖12(b)、(c)所示.

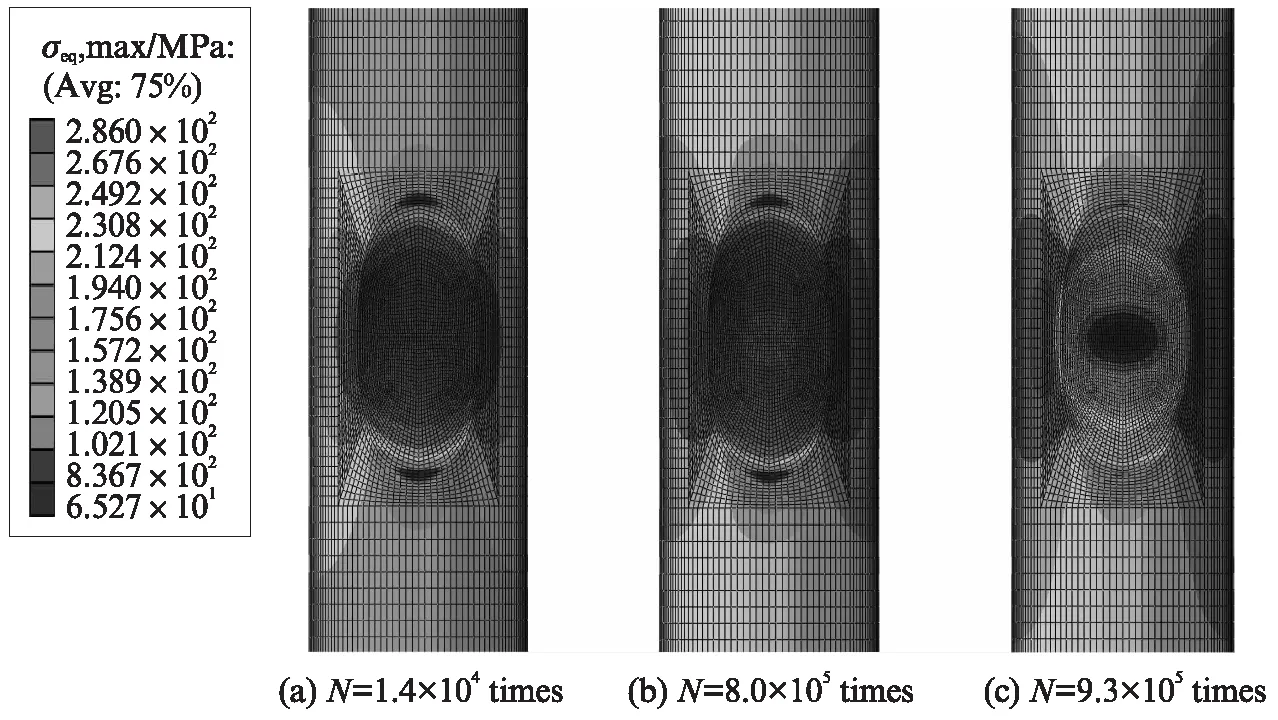
圖12 試件CF2有限元模型σeq,max的分布Fig.12 Distribution of σeq,max of specimen CF2 FE model

這體現了在CDM模型中,材料性能隨著荷載循環而退化是疲勞失效的重要機理.如圖13中紅色的節點所示,在試件CF5表面設定以蝕坑底部為起點,沿鋼筋環向(y方向)到蝕坑外圍的路徑,不同循環次數時沿該路徑的σeq,max的分布見圖14.由圖14可見,疲勞中前期蝕坑內σeq,max值均較高,且變化微小;疲勞后期蝕坑部位的σeq,max顯著降低,而蝕坑外圍區域的σeq,max有所增高,應力重新分布.

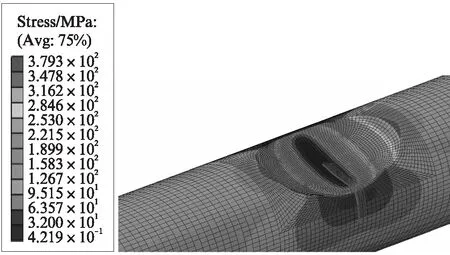
圖13 試件CF5有限元模型路徑的定義Fig.13 Path definition of the specimen CF5 FE model

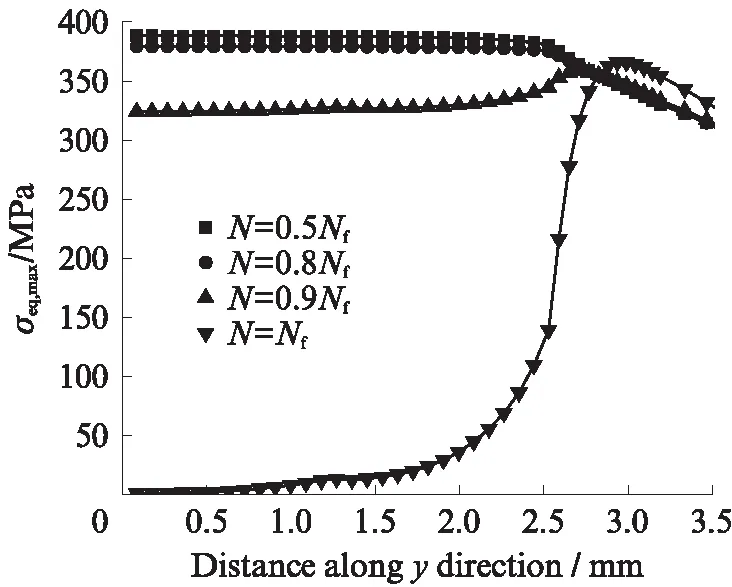
圖14 不同循環次數下沿試件CF5路徑的σeq,max分布Fig.14 Distribution of σeq,max along path of specimen CF5 at different number of cycles

圖15為試件CF1～CF6蝕坑底部處σeq,max隨循環次數的變化.由圖15可見：在疲勞中前期,σeq,max略微降低;當循環次數逐漸接近疲勞壽命時,σeq,max迅速降低,在循環次數達到疲勞壽命時降低至接近0值,意味著疲勞失效.CDM模型能夠反映高周疲勞破壞的突然性.

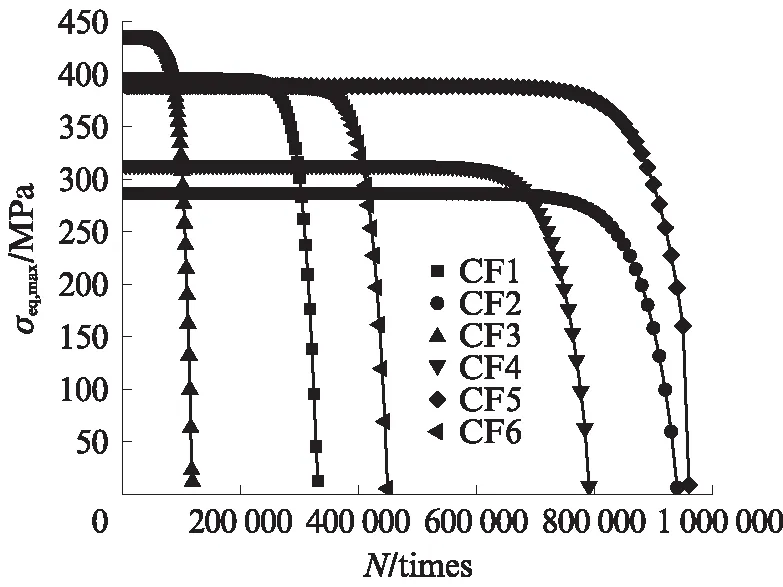
圖15 試件CF1～CF6 蝕坑底部的σeq,max演化Fig.15 Evolution of σeq,max at bottom of pits of specimen CF1-CF6

5 結論

(1)將CDM模型引入坑蝕鋼筋高周疲勞的研究中,通過鋼筋試件疲勞試驗和數據分析,標定了HRB400鋼筋的CDM模型參數.在Abaqus平臺上通過二次開發編寫了CDM模型的Umat程序.

(2)CDM模型和Umat算法預測疲勞壽命與試驗值吻合較好.應力場和損傷場的演化表明,鋼筋蝕坑處應力集中加劇了疲勞損傷發展,疲勞前期和中期損傷發展緩慢,疲勞后期疲勞損傷迅速累積、擴展;由于材料性能退化,蝕坑部位發生了應力重分布,蝕坑底部的應力在疲勞后期迅速卸載,而其外圍應力有所升高.

(3)主要考慮了基于彈性損傷的高周疲勞,當蝕坑處因應力集中而達到塑性階段時,則需要考慮彈塑性疲勞損傷演化.CDM方法適用于不同蝕坑尺寸和不同應力水平下坑蝕鋼筋的疲勞分析,具有良好的應用前景.