一種帶形狀參數的奇異混合擬Bézier曲線*

張貴倉，拓明秀，蘇金鳳，孟建軍,韓根亮

(1.西北師范大學數學與統計學院，甘肅 蘭州 730070；2.蘭州交通大學機電技術研究所，甘肅 蘭州 730070；3.甘肅省傳感器與傳感技術重點實驗室，甘肅 蘭州 730030)

1 引言

Bézier和B樣條方法是計算機輔助幾何設計CAGD(Computer Aided Geometric Design)的2種主流方法，因具有幾何不變性、保凸性等實用性質而被廣泛地應用于曲線曲面設計。然而傳統的Bézier和B樣條曲線曲面已很難滿足快速發展的幾何工業的多元需求。隨之，許多有理化形式的Bézier曲線被提出，但該類曲線存在漸進的問題，并且權因子使用不當容易破壞幾何形狀[1,2]。為解決此類問題，學者們提出了許多帶有形狀參數的類Bernstein基和B樣條基[3 - 11]。

文獻[12]將參數引入控制頂點構造出了一組帶形狀參數的擬Bézier曲線，并從光順性的角度出發在能量優化的理論基礎上對形狀參數的取值給出了實用性建議。文獻[13]在代數多項式空間中構造了一組類Bernstein基函數，其對應生成的曲線具有幾何不變性和保凸性等性質。文獻[14]基于文獻[13]中的基函數提出了帶多個形狀參數的擬三次Bézier曲面。文獻[15]在三角多項式空間中構造了一類帶形狀參數的Bernstein-Bézier曲面片。文獻[16]將文獻[3]中的基函數擴展到三角域上得到了三角域上帶3個形狀參數的基函數，并給出了形狀可調性的三角域曲面。文獻[17]利用奇異混合技術構造了一種簡單直觀的線性奇異混合樣條曲線，但未全面討論曲線的連續性及參數對曲線的影響。文獻[18]將奇異混合技術加入三次λμ-α-DP曲線得到了具有幾何連續性的線性奇異混合的三次λμ-α-DP曲線，但該曲線存在不能精確表示橢圓等二次曲線的缺點。

傳統Bézier曲線具有單位性、對稱性等優良性質，但往往不能精確表示橢圓弧等二次曲線。為了解決傳統曲線出現的問題，本文將奇異混合函數和三角多項式空間中的擬三次三角Bézier基函數相結合，得到了一種帶有形狀參數的奇異混合擬Bézier曲線。新構造的曲線具有規范性、凸包性和幾何不變性等重要性質的同時還具有靈活的形狀可調性，且滿足一定條件時2段奇異混合擬Bézier曲線能夠達到G1及G2連續。新曲線能夠克服傳統的Bézier方法未能準確表示除拋物線外的圓錐曲線這一缺點。此外，基于傳統的NURBS(Non-Uniform Rational B-Splines)曲線表示形式能夠與傳統Bézier曲線進行轉化，本文方法與NURBS表示也具有較好的兼容性[19]。

2 奇異混合函數的構造

2.1 奇異混合函數的定義

定義1設f(t)是定義在函數自變量t∈[0,1]上的一個連續函數，如果f(t)滿足如下條件:

f(0)=1,f(1)=0,

f(k)(0)=f(k)(1)=0,k=1,2,…,n

(1)

那么可以稱f(t)是n階奇異混合函數。

稱滿足式(1)且次數最小的多項式為最小奇異混合函數。

2.2 一般奇異混合函數的建立

根據定義1可知，n階奇異混合函數至少要滿足2n+2個條件，因此要求一個n階奇異混合函數可以按照如下方法進行。

設S為某函數空間的一個子空間，并有:

S=span{φ0(t),φ1(t),…,φ2n+1(t)},

φk(t)∈Cn[0,1]

其中φ0(t),φ1(t),…,φ2n+1(t)在[0,1]線性無關，則可設奇異混合函數為:

其中，ak(0≤k≤2n+1)為式(6)中線性方程組的系數，φk(t)(0≤k≤2n+1)代表線性方程組的未知量。

由定義1可得:

(2)

(3)

(4)

(5)

若令:

φk,j=φk,k=1,2,…,2n+1;j=0,1

則由式(2)～式(5)組成的方程組可以寫成如下形式:

(6)

求解式(6)就可得到所需的奇異混合函數。

3 奇異混合擬Bézier曲線的定義

文獻[20]證明了當系數λ,μ∈(-2,1],t∈[0,π/2]時，基函數:

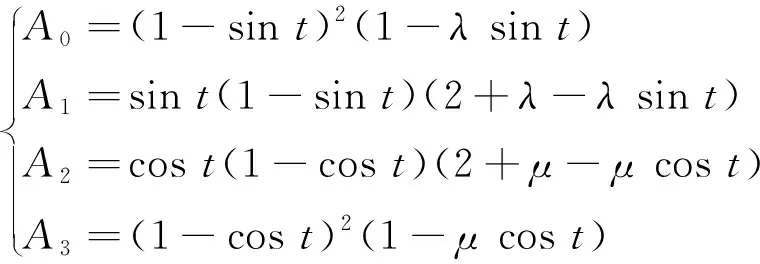
(7)

為擬三次三角多項式空間Pλ,μ=Span{1,sin2t,(1-sint)2(1-λsint),(1-cost)2(1-μcost)}中的最優規范全正基，稱式(7)所給出的基函數為三次三角Bézier基函數。若令t∈[0,1]，式(7)中的基函數可以改寫為:

(8)

基于該基函數對曲線曲面形狀控制的有效性，利用奇異混合函數和權的思想構造出一種奇異混合擬Bézier曲線。

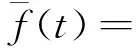
Q(t)=α(t)P(t)+(1-α(t))L(t),0≤t≤1

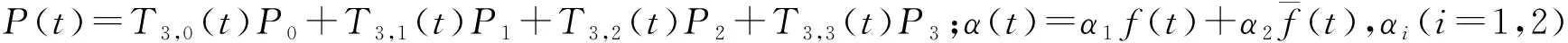
由定義2易知奇異混合擬Bézier曲線Q(t)含有4個參數α1,α2,λ,μ，通過改變它們的值就可以調節曲線的形狀。為方便討論稱α1,α2為混合參數，λ,μ為形狀參數。

4 奇異混合擬Bézier曲線基函數

4.1 奇異混合Bézier曲線基函數的表示

根據定義2所給的曲線表達式，可將三次奇異混合擬Bézier曲線進一步表示為:

Q(t)=α(t)P(t)+(1-α(t))L(t)=

T3,1(t)P1+T3,2(t)P2+T3,3(t)P3)+

若記

(9)

(10)

(11)

(12)

則

(13)

由式(3)知{Di(t,α1,α2,λ,μ)|i=0,1,2,3}具有權性。

引理1最小奇異混合函數在1/2處是一個不動點，即:

f(1/2)=1/2

定理1設f(t)為n(n>0)階最小奇異混合函數，則{Di(t,α1,α2,λ,μ)|t∈[0,1],i=0,1,2,3}線性無關的充分必要條件是:

證明充分性。

設ξ0,ξ1,ξ2,ξ3為任意實數，若有:

(14)

根據最小奇異函數在端點及1/2處的性質，則有:

α1ξ0+(1-α1)ξ1=0

(15)

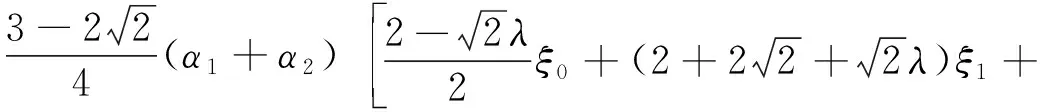
α2ξ3+(1-α2)ξ2=0

(16)

對式(14)求一階導數，得:

根據奇異混合函數的性質及它在0與1處的導數為0，得:

(17)

(18)

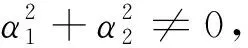
必要性。

D0(t,α1,α2,λ,μ)=D1(t,α1,α2,λ,μ)=0

顯然函數組{Di(t,α1,α2,λ,μ)|i=0,1,2,3}是線性相關的，因此定理得證。

□

因{Di(t,α1,α2,λ,μ)|i=0,1,2,3}具有權性及線性無關性，故可視其為一組基函數。所以，奇異混合擬Bézier曲線可以由該基表示為:

4.2 奇異混合擬Bézier基函數的性質

奇異混合擬Bézier基函數具有下列性質：

性質1規范性：

性質2非負性：對于0≤α1,α2≤1，λ,μ∈(-2,1]，則有Di(t,α1,α2,λ,μ)≥0。

性質3端點性質：

D0(0,α1,α2,λ,μ)=α1

D0(1,α1,α2,λ,μ)=0

D1(0,α1,α2,λ,μ)=1-α1

D1(1,α1,α2,λ,μ)=0

D2(0,α1,α2,λ,μ)=0

D2(1,α1,α2,λ,μ)=1-α2

D3(0,α1,α2,λ,μ)=0

D3(1,α1,α2,λ,μ)=α2

性質4對稱性：

D0(t,α1,α2,λ,μ)=D3(1-t,α2,α1,μ,λ)

D1(t,α1,α2,λ,μ)=D2(1-t,α2,α1,μ,λ)

性質5退化性：若α1=α2=1，則奇異混合擬Bézier基函數退化為三次T-Bézier基函數；若α1=α2=1且λ=1,μ=1，則奇異混合擬Bézier基函數退化為三次類Bézier基函數。

4.3 奇異混合函數及參數對奇異混合擬Bézier基函數的影響

由式(9)～式(12)能夠看出，奇異混合擬Bézier基函數不僅與參數α1,α2,λ,μ有關，而且與奇異混合函數也有關。下面分析奇異混合函數及參數對奇異混合擬Bézier基函數的影響。

當α1=α2=1時，奇異混合擬Bézier基函數即為式(11)所給最優規范全正基，此時奇異混合函數對奇異混合擬Bézier基函數沒有影響。而由式(9)～式(12)不難發現，參數λ影響基函數D0,D1，參數μ影響基函數D2,D3，圖1b和圖1c分別給出了參數λ和μ的值依次增大對基函數D0,D1和基函數D2,D3的影響。當α1≠α2≠1時，參數λ和μ對基函數D0,D1,D2,D3的影響均與圖1b和圖1c類似，因此在下面的討論中將視參數λ和μ為定值。

當α1=α2=0時，有：

D0(t,α1,α2,λ,μ)=D3(t,α2,α1,λ,μ)=0

此時的4個基函數是線性相關的，從某種程度上來說不能嚴格稱之為基函數，這里不加以嚴格區分。圖1d給出了這種情況的基函數圖像。

Figure 1 Influence of parameters on singular blending quasi-Bézier basis function圖1 參數對奇異混合擬Bézier基函數的影響

當α1,α2在0～1變化時，不同的奇異混合函數對基函數的影響并不明顯。式(19)和式(20)是利用2.2節的方法構造的二次及五次最小多項式奇異混合函數：

f(t)=1-10t3+15t4-6t5

(19)

f(t)=(1-t)11+11t(1-t)10+

55t2(1-t)9+165t3(1-t)8+

330t4(1-t)7+462t5(1-t)6

(20)

圖2給出了α1,α2取值不同的情況下最小多項式奇異混合函數對奇異混合擬Bézier基的影響，其中圖2a，圖2c和圖2b，圖2d分別代表二次及五次最小多項式奇異混合函數對基函數的影響。

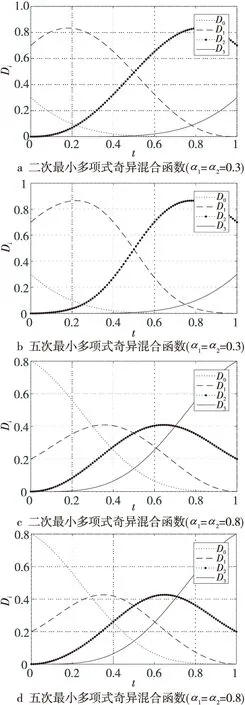
Figure 2 Influence of singular blending function on singular blending quasi-Bézier basis function圖2 奇異混合函數對奇異混合擬Bézier基函數的影響

下面討論奇異混合函數和λ,μ不變時，參數α1,α2對基函數的影響(這里采用式(19)所示的二階最小奇異混合函數，并且λ=μ=1)。

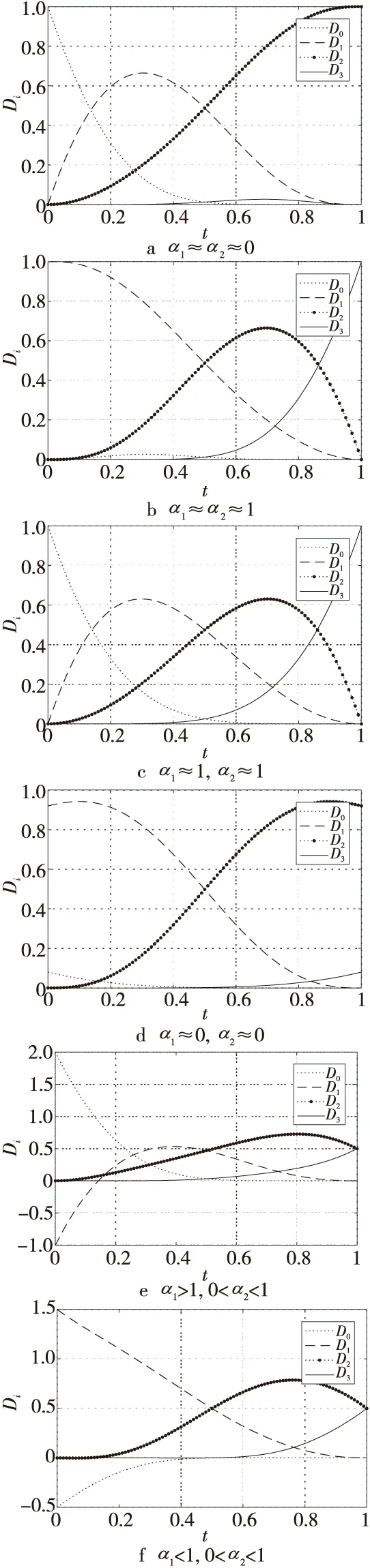
Figure 3 Influence of blending parameters α1,α2 on singular blending quasi-Bézier basis function圖3 混合參數α1,α2對奇異混合擬Bézier基函數的影響

由圖3a～圖3d反映出當α1和α2逼近于1時，奇異混合擬Bézier基函數近似為三次三角Bézier基函數，當α1或α2向0逼近時，奇異混合擬Bézier基函數的D0或D3被嚴重壓縮。由圖3e和圖3f能夠看出,當α1和α2超出0～1時，奇異混合擬Bézier基函數的變化幅度較大。

5 奇異混合擬Bézier曲線的性質

根據奇異混合擬Bézier基函數的性質，可得奇異混合擬Bézier曲線具有如下性質:

性質6端點性質：

R(0)=α1P0+(1-α1)P1

R(1)=α2P3+(1-α2)P2,

(21)

性質7幾何不變性和仿射不變性：由于奇異混合擬Bézier基函數具有規范性，則奇異混合擬Bézier曲線的形狀只取決于控制頂點，而與坐標系的選取無關。

性質9凸包性：當α1,α2∈[0,1]時，由奇異混合擬Bézier基函數的規范性和非負性能夠得到曲線具有凸包性。

性質10逼近性：α1,α2趨于0時，奇異混合擬Bézier曲線向控制多邊形第2條邊逼近。

性質11退化性：當α1=α2=1時，奇異混合擬Bézier曲線形式同三次T-Bézier曲線；當α1=α2=1且λ=μ=1時，奇異混合擬Bézier曲線將退化為三次類Bézier曲線。

性質12非凸包性：當α1,α2?[0,1]時，奇異混合擬Bézier曲線超出控制頂點形成的凸包。

6 參數對奇異混合擬Bézier曲線形狀的影響

6.1 形狀參數λ,μ對曲線形狀的影響

令α1=α2=1，在圖4中λ,μ的取值增大時奇異混合擬Bézier曲線向控制頂點P1或P2趨近。λ不變μ的值越大奇異混合擬Bézier曲線越靠近控制頂點P1。μ不變λ的值越大奇異混合擬Bézier曲線向控制頂點P2趨近的程度越大。圖4～圖9中直角坐標系的橫縱坐標表示控制頂點Pi(i=0,1,2,3)的橫縱坐標。

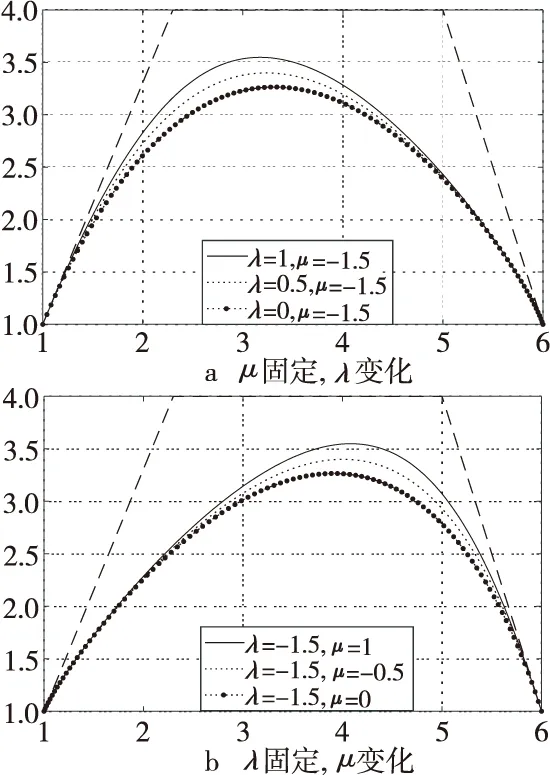
Figure 4 Influence of shape parameters λ,μ on the shape of singular blending quasi-Bézier curves圖4 形狀參數λ,μ對奇異混合擬Bézier曲線形狀的影響

6.2 混合參數α1,α2對曲線形狀的影響

為了更清楚地了解混合參數α1,α2對曲線形狀的影響，令λ=μ=0.5。

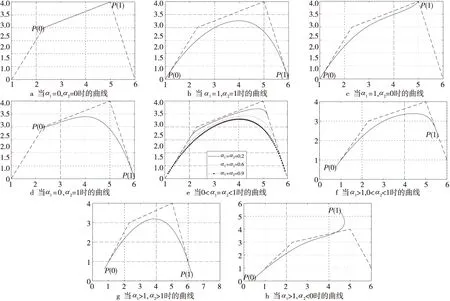
Figure 5 Influence of parameters α1,α2 on the shape of the curve圖5 參數α1,α2對曲線形狀的影響

如圖5a～圖5e所示，當參數α1和α2在[0,1]變化時，奇異混合擬Bézier曲線完全在控制多邊形所形成的凸包內變化。當α1趨于1時，曲線的始點趨于P0，當α1趨于0時，曲線的始點趨于P1。因此，當參數從0變化到1時曲線的始點在P0P1上從P1變化到P0。而當參數α2從0到1變化時，曲線的終點在P2P3上從P2變化到P3。如圖5f～圖5h所示，由于參數α1,α2超出[0,1]，曲線被拉出控制網格的凸包。分析發現，參數α1,α2使得曲線擁有較好張力的同時具有良好的形狀可調性。

7 奇異混合擬Bézier曲線曲面設計

7.1 奇異混合擬Bézier曲線的拼接

在實際造型設計過程中，單個的奇異混合擬Bézier曲線往往無法準確地描述結構復雜的曲線，為保證曲線的光滑性常采用拼接方法。

設2段奇異混合擬Bézier曲線分別為：

其中,Pi,Qi分別為2段奇異混合擬Bézier曲線的控制頂點。

經簡單計算可得:

即R1(1)=R2(0)，則2段奇異混合擬Bézier曲線滿足G0連續。

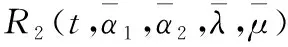
R′2(0)=ξR′1(1),ξ>0

(22)

由性質6可得:

(23)

(24)

將式(23)和式(24)代入式(22)可得：

(25)

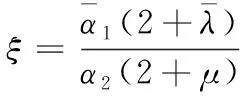
為使2段奇異混合擬Bézier曲線在公共連接點處滿足G2連續，2條曲線滿足G1連續的條件外還要滿足：

R″2(0)=ξ2R″1(1)+δR′1(1)

由端點性質可得：

(26)

則2段奇異混合擬Bézier曲線能夠達到G2連續條件為：式(25)和式(26)。圖6和圖7分別給出了奇異混合擬Bézier曲線的G1和G2連續的圖像。

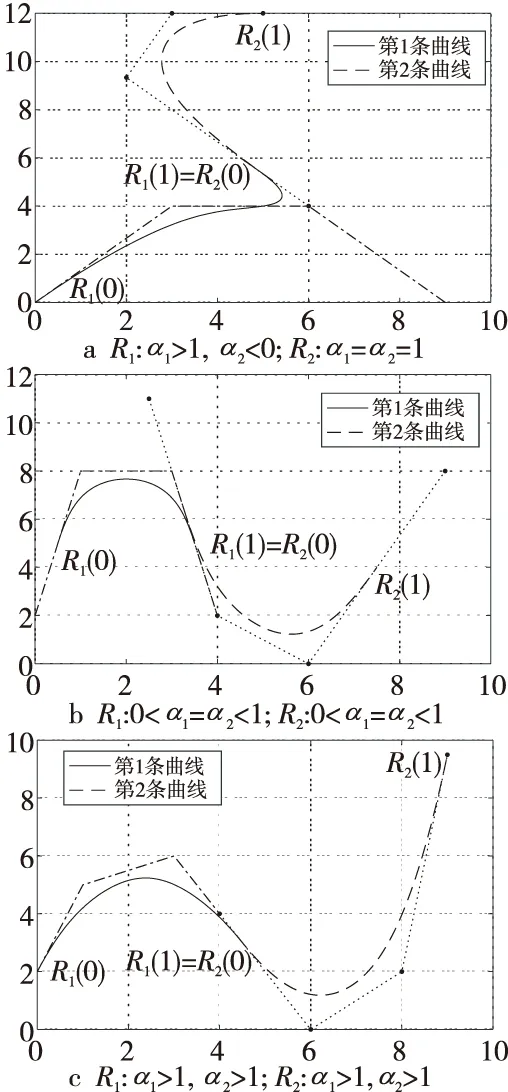
Figure 6 G1-continuous of singular blending quasi-Bézier curves圖6 奇異混合擬Bézier曲線的G1連續

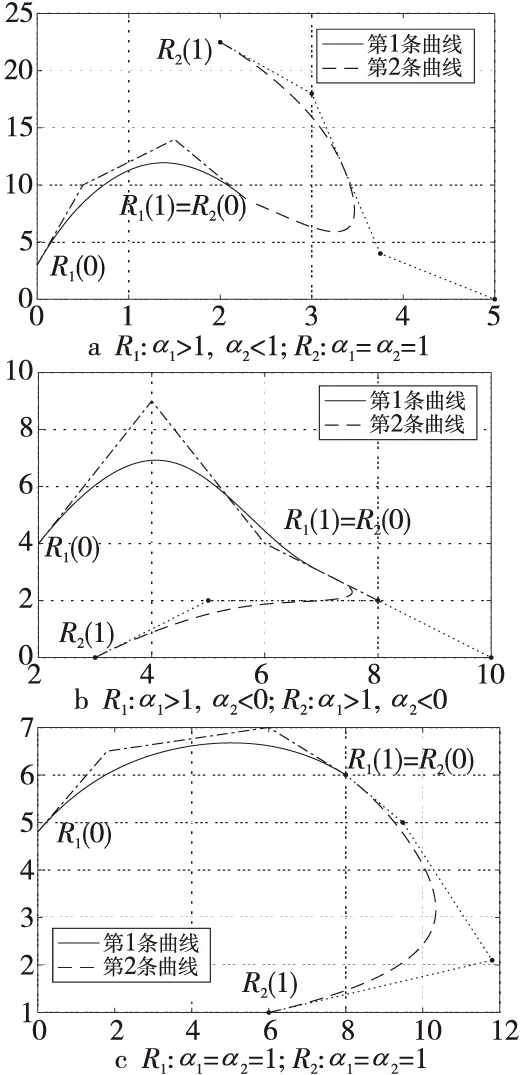
Figure 7 G2-continuous of singular blending quasi-Bézier curves圖7 奇異混合擬Bézier曲線的G2連續

7.2 圓弧、橢圓弧和拋物線弧的精確表示

設控制多邊形頂點為P0=(0,0),P1=(a,0),P2=P3=(2a,b)，令α1=α2=1,λ=0,μ=0，則:

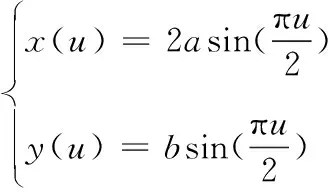
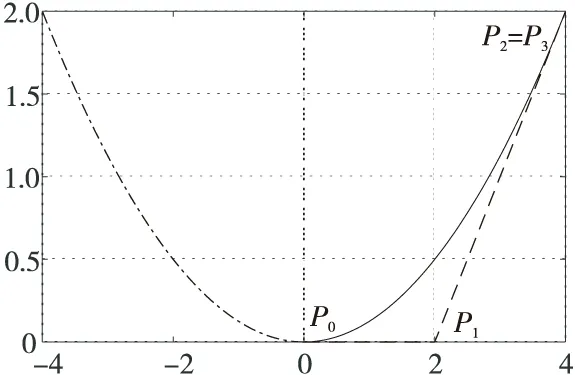
Figure 8 Accurate representation of a parabolic arc圖8 拋物線弧的精確表示

設控制多邊形的頂點為Q1=(0,2b),Q2=(a,2b),Q3=(2a,b),Q4=(2a,0)，令α1=1,α2=1，λ=μ=0,則有:

由此可得橢圓方程為：x2/a2+y2/b2=1,當a=b時，即為圓的方程。圖9中實線部分是奇異混合擬Bézier曲線對圓弧的精確表示。

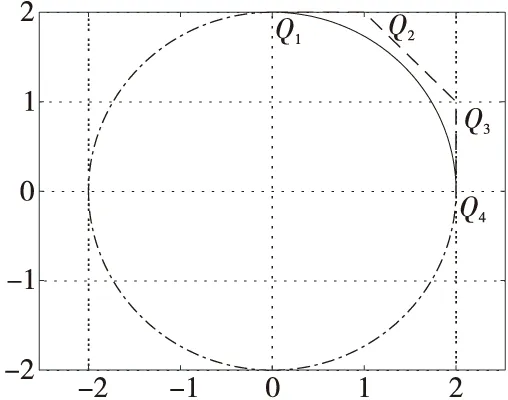
Figure 9 Accurate representation of the arc圖9 圓弧的精確表示

7.3 橢球面的精確表示

用張量積的方法可以將奇異混合擬Bézier曲線推廣至四邊域曲面。其表達式為：

V(t,α1,α2,λ,μ,u,v)=

稱為奇異混合擬Bézier曲面。

若給定合適的控制頂點及參數，則奇異混合擬Bézier曲面能夠精確表示橢球面及球面。給定控制頂點:

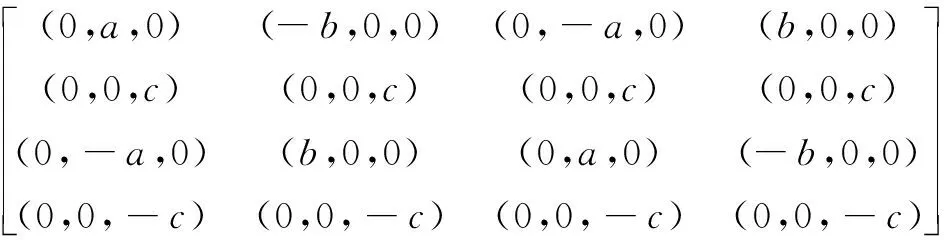
參數α1=α2=1,λ=μ=0時，可得:

當a=b=3/(2c)時表示球面，圖10所示為奇異混合擬Bézier曲面表示的球面片。

Figure 10 Spherical patches represented by singular blending quasi-Bézier surfaces圖10 奇異混合擬Bézier曲面表示的球面片

8 結束語

本文構造了一種帶形狀參數的奇異混合擬Bézier曲線，討論了基函數及曲線的優良性質的同時詳細地分析了奇異混合函數及參數對曲線的影響。本文構造的新曲線不僅有很強的形狀可調性，而且還克服了傳統Bézier曲線不能精確表示圓弧、橢圓弧等二次曲線的缺點。分析及實例表明，新曲線具有很強的實用性與有效性。為滿足復雜曲線曲面造型設計的多元需求，還需對形狀參數域曲線的光順性的關系及曲線曲面的形狀進行更深入的討論(如尖點、拐點、重結點等)，限于篇幅將另文敘述。