基于隨機車流的直、曲線連續梁橋振動響應
吳 迪,黃 俊,周 潔,劉大帥
(南京工業大學 交通運輸工程學院,江蘇 南京 211816)
1 引 言
隨著社會的發展,我國的交通事業以及城市道路也得到迅猛的發展,國家在推行城鎮化的過程中,城市規模也日益增大,道路及橋梁建設在市內及城際交通中的地位也日益重要。曲線梁橋由于其對路線較強的適應性及優美的外觀,在現代化的公路互通式立交及城市道路立交中的應用已十分普遍。在正常狀態下,橋梁不僅要承受結構自重、橋面鋪裝等恒載,還要承受車輛荷載。在所有的荷載中,車輛荷載最為重要也最復雜,是影響橋梁安全性的主要因素。目前,一般直線形式的梁式橋的研究及設計較為成熟,而曲線連續梁橋在結構形式及受力性能上與直線梁橋存在著較大的區別,兩者對車輛荷載(尤其是動力荷載)的響應特征也會有一定的差異。在現有的國內的橋梁設計中,曲線梁橋在一般靜力荷載作用下的設計相對成熟,而其在車輛動力荷載作用下、尤其是實際車流動力荷載作用下的受力及變形性狀仍有待研究,了解曲線梁橋在真實車輛動力荷載作用下的受力特性變化規律有助于指導其設計及維護。
目前國內學者針對連續梁橋與車輛荷載的振動響應開展了大量的研究工作,取得了許多有價值的研究成果。李巖等為提高隨機車流作用下橋梁結構動力行為仿真分析的計算效率,提出一種時變維度的隨機車流與橋梁耦合振動分析方法,聯合模態綜合技術和整體分析法建立了車橋耦合振動方程,并提出了過程分析數據的動態存貯與提取算法。王貴春等以橋面不平順為激勵,對某曲線連續梁橋進行數值分析,研究其在車隊作用下的動力響應,并利用ANSYS編寫迭代計算的APDL命令流求解車橋系統振動微分方程,針對不同工況分析橋梁動力響應。鄧可等基于高速公路車輛動態稱重數據,研究了簡支T梁橋的車載動力效應極值,校驗并評估了現有車輛荷載作用下中小跨橋梁的安全水平,提出了車輛荷載沖擊作用下橋梁效應極值外推方法。王燕等為比較彎橋與直橋的設計差異,根據彎橋承受彎-扭耦合作用的受力特點,分別建立兩組有限元計算模型,通過對比分析計算結果可知,彎橋在外力作用下支反力外側大于內側。并根據計算結果和工程設計經驗提出了設計構造措施。劉星等以某五跨連續曲線箱梁橋為背景,采用有限元軟件建立該橋梁的模型,并建立三軸重型汽車整車模型,分別進行了不同曲率半徑、車速、載重等條件下的曲線梁橋振動響應計算。研究表明:隨著曲率半徑的增加,橋梁跨中位移呈現略微下降的趨勢;車輛行駛速度對跨中的橫向位移及支座的支反力有較大影響。當前對公路橋梁車橋振動響應的研究成果主要集中于確定車載下橋梁結構的動力行為分析方面,這與日常運營狀態隨機車流作用下橋梁的動力響應存在較大的差異,而國內外對隨機車流作用下直、曲線連續梁橋動力行為對比分析的研究還相對較少,研究成果具有一定的局限性。因此,本文以中小跨徑連續梁橋為研究對象,采用VISSIM進行微觀尺度交通流的模擬仿真,充分考慮到路面上不穩定的隨機車流各項參數的隨機性,對隨機車流下的直、曲線連續梁橋的位移、彎矩與扭轉角變化規律進行分析,較為全面地比較直線連續梁橋與曲線連續梁橋對隨機車流響應的不同特征。
2 路網交通仿真分析及橋梁有限元模型構建
2.1 VISSIM仿真及運行評估分析
本文采用VISSIM對連續梁橋區域進行交通仿真,并進行評估分析輸出隨機車流中的車輛實時坐標。在VISSIM仿真分析中,選擇仿真時間、路段編號、車輛編號、車輛坐標等評價指標,獲取隨機車流中不同車輛的實時坐標。針對VISSIM輸出的車輛實時坐標,選擇位于中小跨徑連續梁橋上的車輛(由于連續梁橋在VISSIM中相對路面設置了有一定高差,所以車輛坐標RWorldZ>0的車輛即為位于大橋上的車輛),并將其導入EXCEL表格中,以供進一步分析處理。

圖1 VISSIM仿真流程圖
2.2 橋梁有限元模型建立及模擬計算
本文基于交通流仿真模擬所得到的車輛實時坐標,采用移動荷載動力時程分析考慮車輛荷載作用,利用有限元軟件MIDAS CIVIL模擬計算隨機車流作用下的橋梁的變形及內力。連續梁橋全長為160 m,分為三跨,設置四個支座進行約束,其中一個為固定鉸支座,其余為滑動鉸支座。全橋共劃分為81個節點,單元長度為2 m。
本文基于VISSIM評估分析輸出的車輛實時坐標,利用python語言進行分析,輸出不同仿真時刻(0~20 s,間隔0.1 s)下作用于連續梁橋有限元模型各節點截面的車輛前、后輪數。再結合前、后輪對節點截面荷載作用時程曲線圖,輸出各仿真時刻作用于節點截面的車輛荷載,并定義各節點截面在仿真時間內的時程函數。將時程荷載函數應用到各節點截面,運行有限元模型評估分析,獲得位移、內力等分析結果。
3 直、曲線連續梁橋振動響應規律研究
本課題針對有限元軟件MIDAS CIVIL模擬運算結果進行對比分析,比較直線連續梁橋與曲線連續梁橋對隨機車流響應的不同特征,總結直、曲線連續梁橋在隨機車流作用下的振動響應規律。針對直、曲線連續梁橋在隨機車流作用下位移變化規律,本文從跨中截面豎向位移、豎向位移沖擊系數等方面對位移變化規律進行闡述。
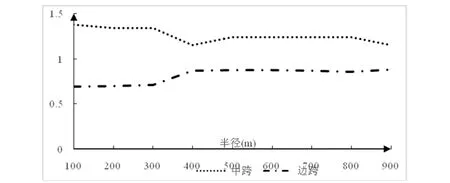
圖3 曲線連續梁橋豎向位移沖擊系數變化圖
在豎向位移方面,由圖2、3可知,在相同的交通荷載作用下,不同曲率半徑下的曲線連續梁橋的豎向位移均大于直線連續梁橋,說明直線梁橋受力性能相較于曲線梁橋更優。隨著曲線梁橋曲率半徑的增大,曲線梁橋豎向位移總體呈現遞增趨勢,曲線梁橋的曲率半徑增至500 m左右時,曲線連續梁橋的豎向位移變化幅度減緩,曲率半徑因素對橋梁的動力特性影響較小。隨著曲率半徑的增大,橋梁中跨跨中截面豎向位移沖擊系數呈現緩慢減小趨勢與邊跨跨中截面沖擊系數變化規律相反。當曲率半徑小于500 m左右時,沖擊系數變化幅度較大,當曲率半徑大于500 m左右時,沖擊系數總體變化平緩,基本不變。
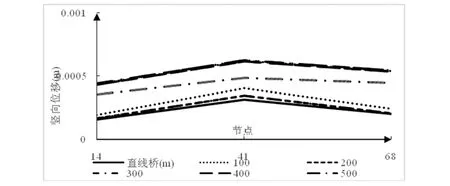
圖2 直、曲線連續梁橋豎向位移比較圖
對于中跨與邊跨跨中截面豎向位移,由圖4可知,當曲率半徑小于400 m時,隨著曲率半徑的增大,曲線梁橋豎向位移呈現出緩慢減小的趨勢,但當曲率半徑大于500 m豎向位移變化幅度不大。不同曲率半徑下的曲線連續梁橋的中跨跨中截面豎向位移均大于邊跨跨中截面豎向位移,這說明連續梁橋的中跨跨中截面相比邊跨跨中截面豎向位移振動幅度更為強烈,在工程實踐中應對中跨跨中截面著重關注。
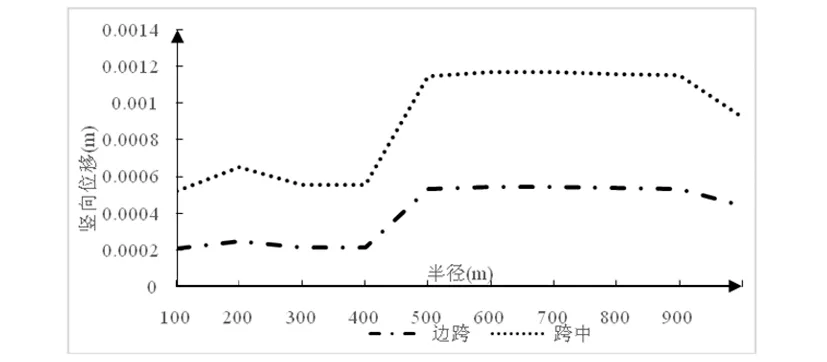
圖4 不同曲率半徑下曲線連續梁橋中跨與邊跨跨中截面豎向位移比較圖
針對直、曲線連續梁橋在隨機車流作用下彎矩變化規律,本文從跨中截面彎矩、彎矩沖擊系數等角度對彎矩變化規律進行探索總結。
對于跨中截面彎矩,由圖5可知,在相同的交通荷載作用下,不同曲率半徑的曲線梁橋的跨中截面彎矩均大于直線連續梁橋,說明直線梁橋受力性能相較于曲線梁橋更優。隨著曲線連續梁橋曲率半徑的增大,曲線橋跨中截面彎矩也在不斷增大,但當曲線梁橋的曲率半徑大于500 m左右時,支座、跨中截面彎矩變化幅度放緩,數值趨于一致,因此,彎矩受曲率半徑的影響較小。
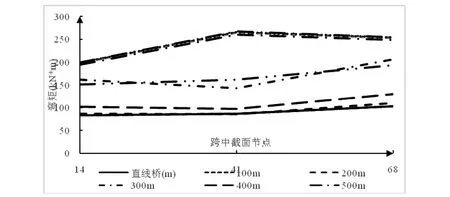
圖5 直、曲線連續梁橋跨中截面彎矩比較圖
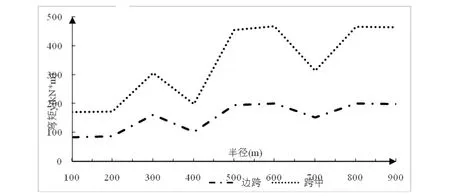
圖6 不同曲率半徑下曲線連續梁橋中跨與邊跨跨中截面彎矩比較圖

圖7 不同曲率半徑下曲線連續梁橋中跨與邊跨跨中截面彎矩沖擊系數比較圖
對于中跨與邊跨跨中截面彎矩沖擊系數,由圖6、7可知,在隨機車流作用下,不同曲率半徑下的曲線梁橋中跨和邊跨跨中截面彎矩整體成上漲趨勢且變化趨勢基本相同,當曲率半徑在400~600 m時,彎矩出現突變,這表明當曲率半徑在400~600 m時,車輛荷載對連續梁橋帶來較大的影響。當曲線梁橋中跨跨中截面彎矩的大小比邊跨跨中截面的彎矩略大,在曲率半徑為500 m時,邊跨跨中截面彎矩值為168.3(KN·m),中跨跨中截面彎矩值為463.1(KN·m),增大了175.2%。說明隨機車流對中跨跨中截面彎矩作用相比邊跨跨中截面明顯,中跨跨中截面的受力情況在工程建設中應多加關注。隨著曲率半徑的增大,當曲率半徑小于400 m時,橋梁邊跨跨中截面的彎矩沖擊系數均呈遞減趨勢,中跨跨中截面的變化規律與之相反。曲率半徑大于400 m時,兩者的沖擊系數曲線趨于穩定,邊跨跨中截面的彎矩沖擊系數穩定至1.14左右,中跨跨中截面的彎矩沖擊系數穩定至0.87左右。
4 結 語
(1)在隨機車流作用下,曲線梁橋相較于直線梁橋的振動響應更為顯著,位移和彎矩均大于直線梁橋,因此在設計曲線梁橋時,應更加關注車輛荷載給曲線梁橋帶來的影響;(2)基于本文的研究工況,中跨跨中截面受曲率半徑的影響較大,而邊跨跨中截面受曲率半徑影響微弱。對比中跨跨中截面與邊跨跨中截面,發現中跨跨中的位移和彎矩收到車輛荷載的影響更大;(3)隨著曲率半徑的增大,橋梁振動響應減小。曲率半徑小于一定數值時,其對動力響應的影響顯著。

