UHPC纖維定向法及對受拉性能影響

張 陽，屈少欽，盧九章，霍文斌

(1.湖南大學 風工程與橋梁工程湖南省重點實驗室，湖南 長沙 410082；2.北京市政路橋管理養護集團，北京 100097；3.廣東省建筑設計院有限公司，廣東 廣州 510010)

0 引 言

超高性能混凝土(UHPC)是一種抗壓強度超過150MPa的新型纖維增強水泥基復合材料[1]，原材料組成為石英砂、活性摻合料、惰性摻合料、纖維、高效減水劑、水等。UHPC基于最大堆積密度理論和纖維增強理論開發，內部分散的短切纖維能有效抑制裂縫的形成和發展，提高UHPC的抗拉性能。

通常UHPC內纖維取向呈現亂向分布，如果讓纖維取向傾斜于受拉方向，其抗拉強度、韌性和阻裂性能會大幅提升[2]。現有研究表明，UHPC內纖維取向傾向于澆筑UHPC時，新拌UHPC流動的方向[3]。部分學者[4-6]根據這一特性，通過特殊的澆筑手段，讓新拌UHPC在模具中流動，實現纖維定向的效果。另外鋼纖維作為一種導磁性介質，慕儒[2]等采用電磁場作用實現了UHPC的纖維定向，相較于流動澆筑法，UHPC的受拉性能提升更大。同時，纖維定向會導致UHPC在纖維取向以外的力學性能降低[7]，因此，在雙向受力板、復合受力構件(牛腿、剛節點等)以及其他復雜受力結構中，應盡量避免采用定向纖維UHPC，但如果將其用于軸向受力構件(如桁架受拉桿)時則具有明顯的優勢。

確立UHPC受拉性能與纖維取向之間的關系是開發應用定向纖維UHPC的關鍵之一。研究人員試圖量化纖維取向的參數與UHPC受拉性能之間的聯系，參數如表1。B.BOULEKBACHE[3]、L.FERRARA 等[7]提出的纖維取向系數θ被廣泛作為評價纖維取向程度的指標，他們發現UHPC的受拉性能隨著纖維取向系數的增加而提高；F.GERMANO[8]提出的取向數η和S.T.KANG[4]等提出的纖維取向因子ηφ也得到了較為廣泛的認可，這兩個指標與UHPC的受拉性能表現同樣正相關；G.TIBERTI[9]綜合了相關纖維取向指標，提出了更加合理的纖維增強效率比ρf,eff，并發現UHPC的斷裂能與該指標存在線性關系。試驗表明，上述指標均與UHPC受拉性能存在某種聯系，但是尚無確切的計算公式將UHPC的抗拉強度與纖維取向指標聯系起來。H.H.HUANG[10]等根據試驗結果擬合得到近似的線性回歸方程，但其普遍適用性還有待進一步驗證。

表1 纖維取向評估方法

基于研究現狀，筆者提出了一種用于UHPC纖維定向澆筑的方法，并采用圖像分析技術[4,11]和UHPC軸拉試驗，重點分析纖維定向澆筑對UHPC內纖維取向分布的影響，以及纖維取向分布與UHPC抗拉強度之間的定量關系。

1 定向澆筑

試驗選擇體積摻量3%的鋼纖維增強UHPC，由于較高纖維摻量會導致UHPC工作性和流動性降低，直接讓UHPC在模具中流動會變得十分困難。筆者設計了一套澆筑裝置，用于UHPC的纖維定向澆筑，如圖1。

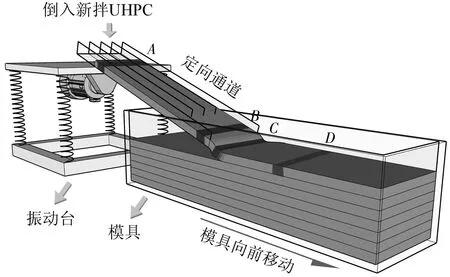
圖1 UHPC纖維定向澆筑裝置

定向裝置主要由定向通道、振動臺及可移動的模具組成。定向通道的作用是讓新拌UHPC在進入模具前產生一個流動的過程，從而改變新拌UHPC內纖維的取向分布；振動臺的作用是克服由于UHPC工作性差引起的澆筑問題，當振動臺未啟動時，倒入斜置的定向槽的新拌UHPC難以流動，啟動振動臺并將定向槽斜置在振動臺上，新拌UHPC能夠快速沿著定向槽流下，保證了UHPC纖維定向的可實施性。

UHPC纖維定向澆筑的具體流程大致如下：首先，啟動振動臺，將定向通道斜置在振動臺上，倒入新拌UHPC至定向通道上方，UHPC在振動作用下快速下流；然后，持續移動模具并保證足夠的移動速率，以提供一個額外的拖拽作用，并迅速鋪滿一層；重復上述過程，通過定向澆筑多層以填滿模具內部。

纖維定向澆筑中有兩個方面改變UHPC內纖維的取向分布。一方面新拌UHPC在定向通道中流動的速度梯度[3]，這一作用發生在圖1中AB點之間。通道邊壁的限制使得UHPC在通道流速隨著與邊壁的距離的增大而增加，從而形成速度梯度，原理如圖2；當纖維方向與流動方向存在一定夾角時，速度梯度就會帶動纖維向流動方向旋轉。

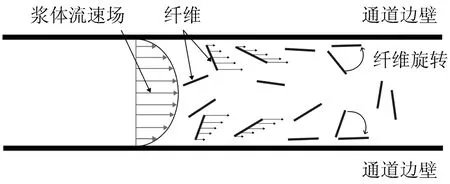
圖2 纖維在新拌UHPC流速場中旋轉

另一方面新拌UHPC從定向通道流入模具過程中受到的拖拽作用，主要發生在圖1中C點處。在纖維定向澆筑過程中，為了讓流入模具中的UHPC能夠順著UHPC流動方向鋪筑，應讓定向通道不斷與模具之間發生相對移動，當相對移動速度大于新拌UHPC的流動速度時，新拌UHPC在C點處由于速度差，產生較大的塑性變形，導致新拌UHPC沿受拉方向的長度增大，垂直流動方向的長度減小。這種塑性變形導致新拌UHPC內的鋼纖維傾角進一步減小。

2 試驗概述

試驗所用UHPC原料配合比如表2，按不同澆筑方式設計了兩組試件，其中一組試件(記為A-UHPC)采用1節所述纖維定向法澆筑，振動臺頻率為50 Hz，纖維定向通道由1 mm厚304不銹鋼制成，幾何尺寸如圖3，其中18 mm指單個通道的內寬，其余尺寸均為外部尺寸。按照纖維定向方式澆筑試件，實測新拌UHPC需要6～8 s通過完整的纖維定向通道，平均流速為0.063～0.083 m/s，填滿100 mm厚的試件需14～17層，共耗時42～68 s。另一組試件(記為R-UHPC，原料相同)采用普通的澆筑方式澆筑，普通澆筑時，新拌UHPC直接從模具中間位置倒入。澆筑完成后，所有試件均覆膜在室內養護48 h后拆模，拆模后的試件繼續在室內(溫度20～30 ℃、澆水后濕度80%左右)覆膜澆水養護至28 d齡期。

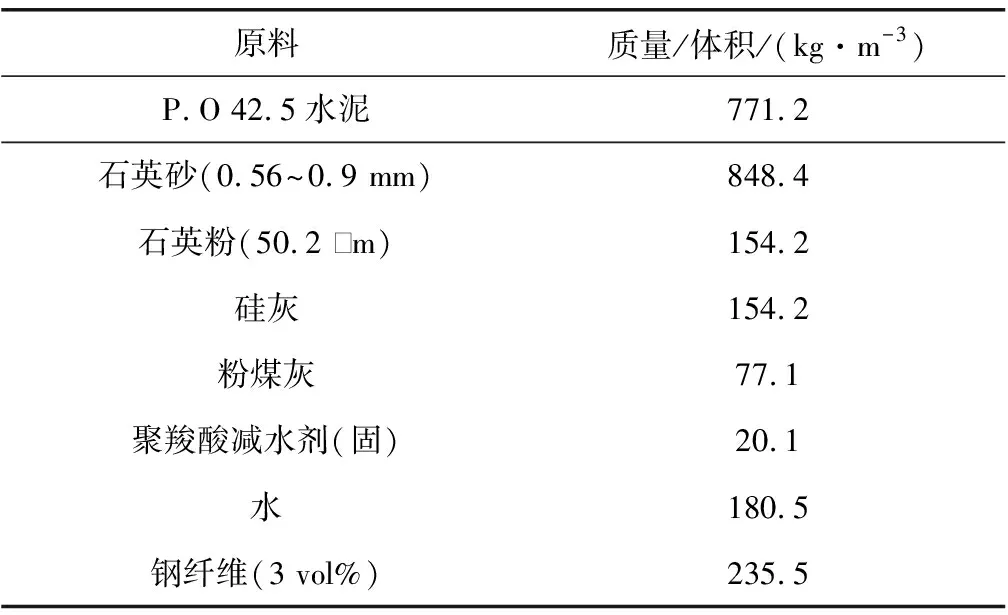
表2 UHPC原料配合比

圖3 纖維定向通道幾何尺寸

每組試件分別包含3個抗折試件和3個軸拉試件，抗折試件尺寸(100 mm×100 mm×400 mm)和加載制度參照法國推薦標準NF P18-470[12]附錄D中的切口試件四點抗彎試驗，加載的裝置如圖4(a)。加載時試件跨徑為300 mm，兩個對稱加載點間距100 mm，跨中設置有千分表測量抗折試件的跨中撓度，加載速率為0.15 mm/min。軸拉試件的尺寸和加載裝置如圖4(b)，測量段橫截面積為50 mm×100 mm，測量長度為150 mm，試件兩側分別固定有位移計測量UHPC的整體延伸量，加載速率為0.015 mm/min。

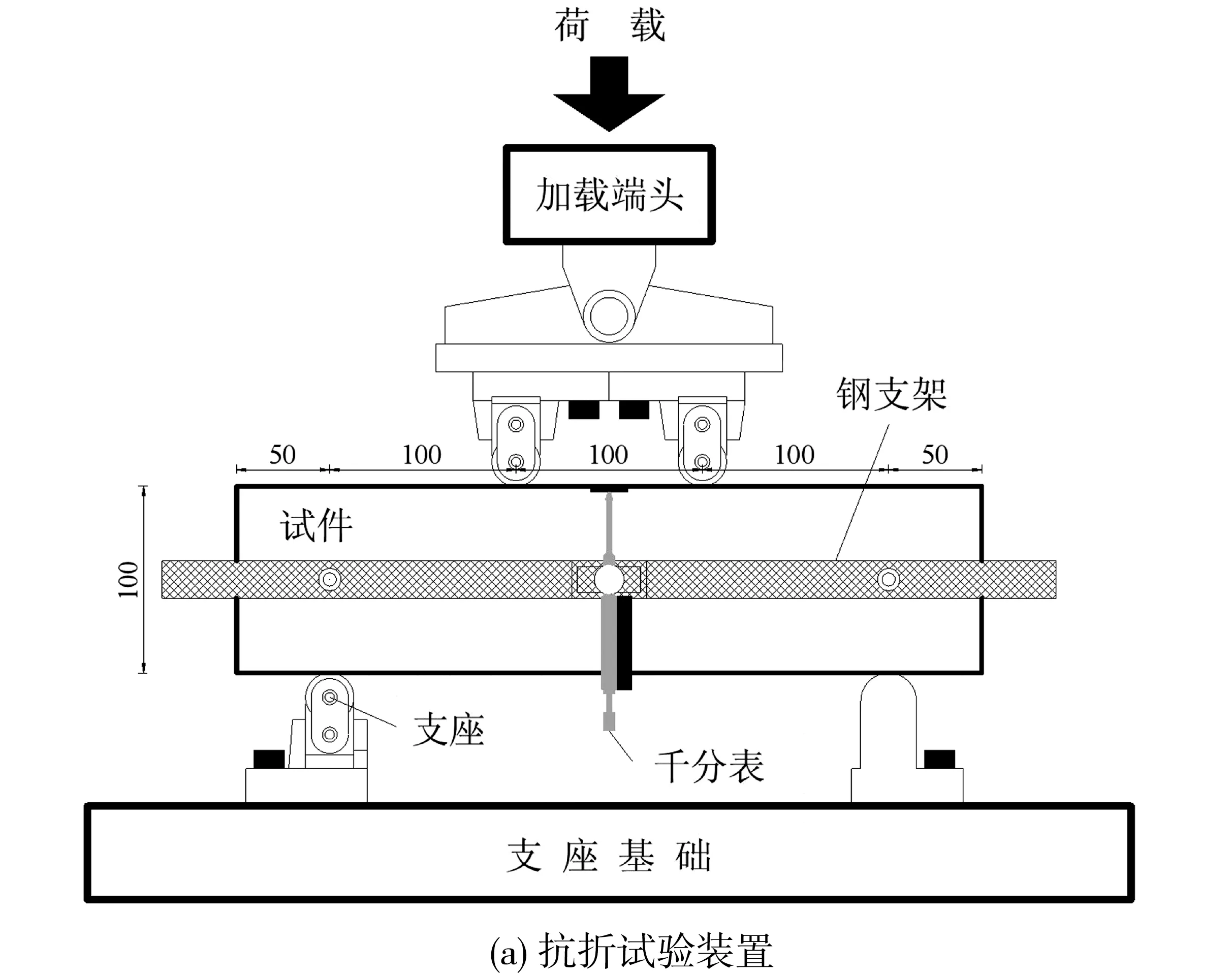
圖4 試驗試件尺寸及加載裝置

3 UHPC纖維取向評估方法

3.1 圖像處理

圖像處理、透射X射線、CT成像，以及AC-IS都被用于分析UHPC中鋼纖維的分布與取向[14]。其中，圖像處理技術被認為是測試纖維分布與取向最實用、簡便的方法。圖像處理[12]通過對試件切片并拍照，獲取切面圖像信息，然后采用計算機對圖像信息做二值化處理，提取UHPC切面上纖維的截面形狀，計算纖維的傾斜角度，最終獲得整個截面上的纖維取向分布。圖像處理對原始圖像清晰度要求較高，實際計算精度依賴計算機算法的合理性，通常計算結果與實際纖維取向存在一定差異，但不影響纖維的整體取向分布形式。

抗折試件或軸拉試件受拉破壞后，垂直于受拉方向切開未破壞的橫截面并拍照，得到橫切面原始圖像如圖5。由圖5可知，R-UHPC的橫切面纖維分布較稀疏，纖維切面形狀較扁平，多呈扁平橢圓狀，說明大部分纖維傾角偏大；A-UHPC橫切面纖維分布較R-UHPC而言更加密集，纖維數量明顯增多，纖維切面形狀更接近圓形，大部分纖維傾角偏小。還可以看到，A-UHPC纖維分布有較為明顯的層次感，這是因為分層定向澆筑，一定程度上會影響UHPC的整體性。

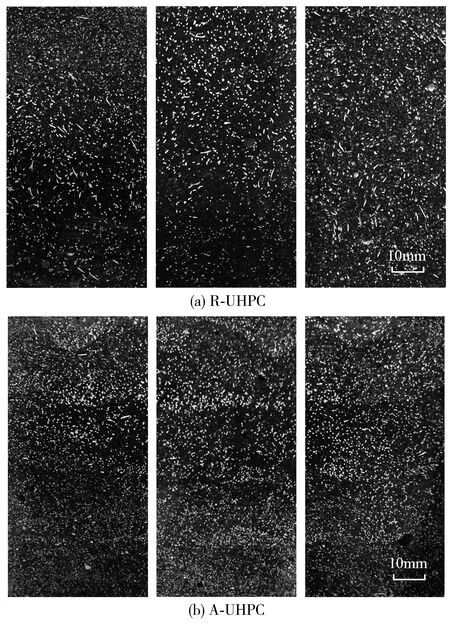
圖5 UHPC切面纖維分布原始圖像

通過計算機圖像處理技術[4,11]，可以得到橫切面上所有鋼纖維與截面法線夾角(即纖維傾角)，統計得到過橫切面纖維傾角分布頻率直方圖如圖6。值得注意，通過某個橫切面整合得到的纖維取向分布，只反映通過該橫切面的纖維取向分布，但與UHPC內整體纖維的取向分布有一定的函數關系，故需要對數據進一步分析。

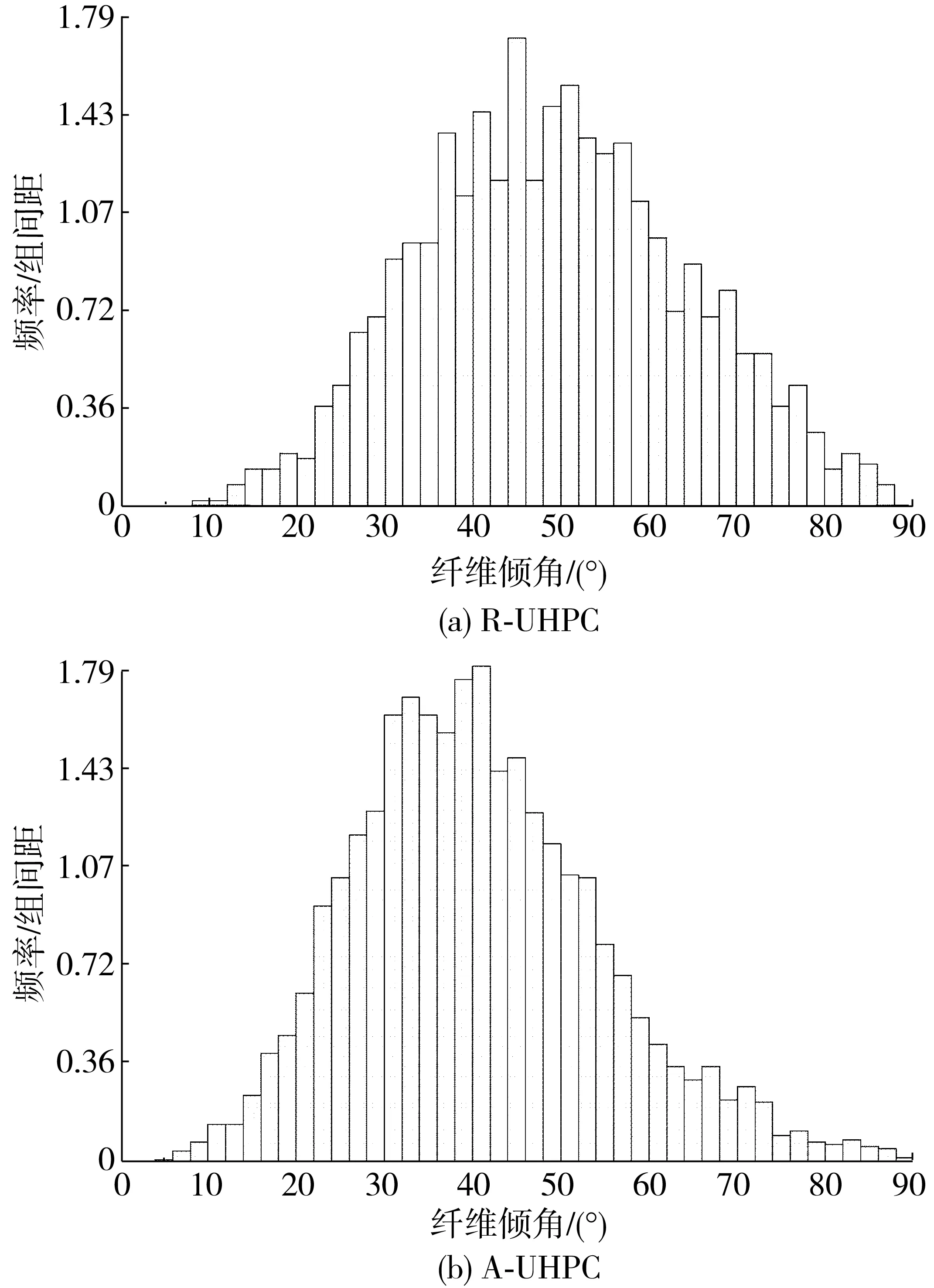
圖6 切面纖維傾角頻率分布直方圖

給定任意橫切面，纖維與橫切面的空間位置關系如圖7，其中lf為鋼纖維長度，φ為鋼纖維傾角。纖維與橫切面的空間位置關系可分為3種：①實際過橫切面的鋼纖維，即圖像分析的橫切面上包含的鋼纖維；②未過橫切面的鋼纖維，但是如果讓它沿形心旋轉一定角度，有可能穿過橫切面，這種鋼纖維的形心位置距離橫切面不大于lf/2；③即使繞形心旋轉一定角度也不能過橫切面的鋼纖維，這種鋼纖維的形心位置距離橫切面大于lf/2。

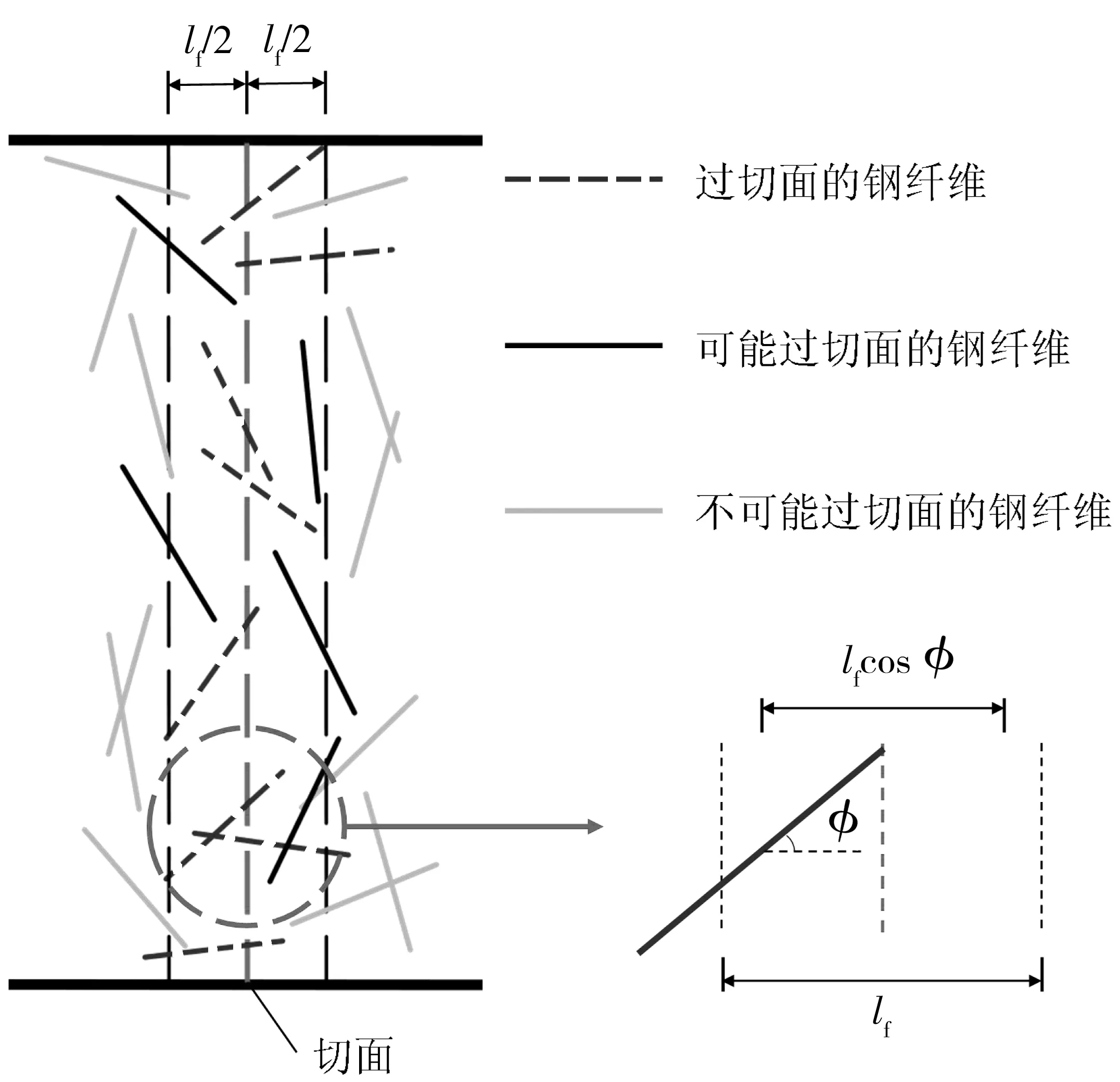
圖7 纖維與切面空間關系

將UHPC內部空間用間隔lf的平行平面切割為若干空間，假設鋼纖維形心在UHPC內部空間隨機均勻分布，那么每一份空間中鋼纖維都可以代表UHPC內部整體的鋼纖維。取其中某個空間Ω，并設定空間中部的平面為切面，則上述前2種鋼纖維為空間Ω內包含的所有鋼纖維，其取向分布可代表UHPC整體鋼纖維的取向分布。假設鋼纖維形心位置距離橫切面為z，空間Ω內鋼纖維形心的概率密度函數[14]如式(1)：

(1)

設空間Ω內鋼纖維傾角為φ為事件A，則與纖維取向的概率密度函數p(φ)的關系如式(2)：

P(A)=p(φ)

(2)

當傾角為φ的鋼纖維與橫切面相交時，其形心位置距離橫切面小于lfcosφ/2，假設空間Ω內的鋼纖維穿過橫切面為事件B，則有：

(3)

則空間Ω內鋼纖維穿過橫切面概率如式(4)：

(4)

圖像分析測量得到的纖維傾角為φ的概率，實際上是指過橫切面鋼纖維中傾角為φ的概率，即P(A|B)，筆者用psec(φ)表示。根據貝葉斯定理，可知p(φ)與psec(φ)的關系如式(5)：

(5)

式(5)中P(B)包含了未知量p(φ)，為了求解P(B)，需要利用概率密度函數的性質，如式(6)：

(6)

故P(B)的計算如式(7)：

(7)

橫切面圖像處理分析得到的纖維傾角頻率直方圖可近似作為psec(φ)。根據式(5)、(7)，UHPC內整體纖維取向分布頻率直方圖、及對應的均值φm如圖8。由圖8可知，R-UHPC和A-UHPC的纖維取向分布具有明顯的差別。R-UHPC纖維傾角均值為56.9°，且大部分集中在50°以上，整體分布形狀接近于cos函數；A-UHPC纖維傾均值為47.3°，明顯小于R-UHPC的傾角均值，且主要分布在30°～50°間，整體分布形狀接近于sin函數。

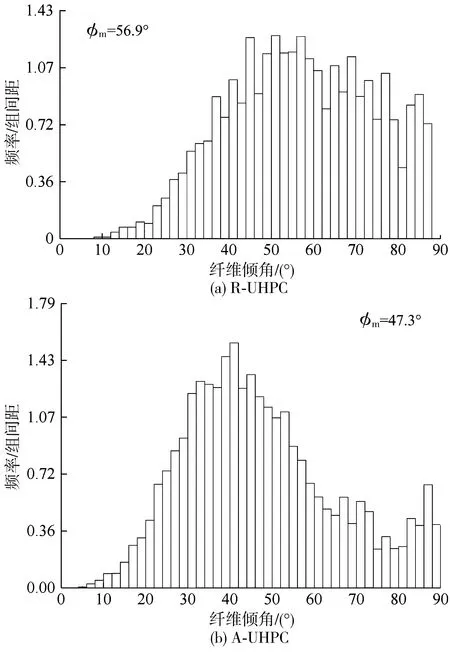
圖8 整體纖維傾角頻率分布直方圖

3.2 纖維取向系數

圖像處理分析不僅可以得到橫切面上纖維取向的分布特征，同時也可以得到橫切面上纖維數量。部分學者采用纖維取向系數θ[15]表征UHPC的纖維定向程度，如式(8)：

(8)

式中：nf為橫切面上纖維數量；Af為纖維的橫截面積；Vf為纖維的體積摻量，筆者取Vf=0.03；A為橫切面面積(抗折試件為100 mm×100 mm，軸拉試件為50 mm×100 mm)。

由式(8)可知，當纖維橫截面積與纖維摻量一致時，纖維取向系數與單位面積的纖維數量nf/A(纖維密度)成正比。

圖像處理分析統計得到纖維密度以及取向系數如表3。由表3可知，R-UHPC橫切面上的纖維密度及取向系數明顯小于A-UHPC橫切面，后者與前者之比約為1.5。UHPC的抗拉強度以及阻裂性能主要由裂縫處纖維的橋聯作用決定，式(8)中的nf表明，纖維定向澆筑對UHPC抗拉性能提升的主要原因是提升了UHPC開裂面處的纖維數量密度，從而整體提升UHPC的抗拉強度和開裂性能。

表3 UHPC纖維密度及取向系數

4 UHPC受拉性能

4.1 力學模型

UHPC受拉破壞發生在主裂縫處，通過主裂縫面的纖維橋聯作用是承擔拉力荷載的主要載體，可認為當UHPC達到極限強度時，所有荷載都通過主裂縫處的纖維傳遞[14]。因此UHPC的抗拉強度ft,UHPC可以用模型進行計算，如式(9)：

(9)

式中：Pfi為極限荷載下過主裂縫面的第i根鋼纖維承擔的荷載。

單根鋼纖維在拉拔作用下的極限承載力除了與纖維自生特性和纖維-基體界面粘接特性有關外，還與纖維的傾斜角度相關。考慮點觸效應和基體壓碎效應，文獻[14]給出了單根纖維承擔的極限承載力與角度間關系如式(10)：

Pfi=ecφ(cosφ)kPf0

(10)

式中：c、k分別為纖維傾角的點觸效應系數和基體壓碎效應系數；Pf0為傾角為0的纖維極限承載力。

為簡化計算，過切面的纖維所承擔的荷載可以近似用傾角為均值φm的纖維計算荷載，則式(9)所述模型可以簡化為式(11)：

(11)

R-UHPC和A-UHPC的纖維密度和纖維取向系數成正比，因此式(11)中nf/A可以用纖維取向系數。假設R-UHPC的纖維傾角均值φm=φR，纖維取向系數為θR，A-UHPC的纖維傾角均值φm=φA，纖維取向系數為θA，故A-UHPC和R-UHPC的抗拉強度比值如式(12)：

(12)

4.2 試驗驗證

試驗測得的R-UHPC和A-UHPC的強度值如表4。由表4可知，A-UHPC的抗折和抗拉強度均顯著大于R-UHPC，兩者抗折和抗拉強度的比值都在1.6～1.7之間，說明纖維定向有效提升了UHPC極限受拉性能。2種UHPC的抗折與抗拉強度的比均維持在2.5左右，說明UHPC的抗折與C抗拉強度存在一個固定比，且該比值受纖維取向影響較小。

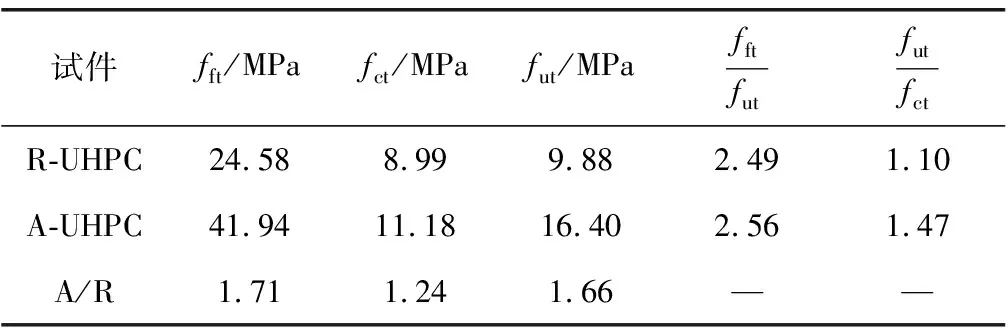
表4 UHPC受拉力學性能指標

纖維定向后的UHPC的抗裂強度得到了顯著提升，A-UHPC與R-UHPC的開裂強度比值約為1.24，說明纖維取向不僅會影響UHPC開裂后的性能，同樣也會影響纖維的阻裂作用，這與部分文獻[4]、[7]一致。R-UHPC抗拉與開裂強度的比值約為1.1，A-UHPC抗拉與開裂強度比值約為1.47。可見R-UHPC在開裂后抗拉強度提升不明顯，而A-UHPC在開裂后的抗拉強度提升顯著。從破壞模式來說，普通方式澆筑的UHPC表現出明顯的低應變硬化特征，纖維定向澆筑則使得低應變硬化UHPC能夠轉變為高應變硬化UHPC。

采用式(12)驗算纖維取向對UHPC抗拉強度的影響，系數取值根據文獻[14]，c=1.6、k=1.8。故根據圖像分析數據，A-UHPC和R-UHPC的抗拉強度比值為：

(13)

計算結果表明，評估模型得到的強度比值為1.69，與表5中試件測得的強度比值1.66十分接近，證明評估模型夠精確評估纖維取向對UHPC抗拉強度的影響，且可以得到一個較為精確的量化值，是一個簡單易用的評價指標。

5 結 論

通過UHPC的纖維定向試驗和纖維取向圖像分析討論了纖維取向對UHPC抗拉強度的影響。通過上述試驗和分析，可以獲得以下結論：

1)采用通道流動結合振動的方式能夠實現UHPC的纖維定向，普通澆筑下UHPC的纖維取向系數為0.487，接近0.5，纖維定向澆筑的UHPC纖維取向系數達到了0.731。

2)采用纖維定向澆筑方式的UHPC相較于普通澆筑的UHPC的開裂強度提升24%，抗拉強度和抗折強度分別提升66%、71%。

3)實測纖維定向使得UHPC的抗拉強度提升了66%，式(12)計算出的強度提升約為69%，排除試驗誤差和外界因素的干擾，可認為式(12)是一個可靠的用以定量評估纖維取向對UHPC抗拉強度影響的指標。