地裂縫作用下管廊結(jié)構(gòu)底部脫空范圍計算方法
鄧博團,田江濤,蘇三慶,李 鑫,李 攀,王 勁
(1.西安科技大學(xué) 建筑與土木工程學(xué)院,陜西 西安 710054;2.西安建筑科技大學(xué) 土木工程學(xué)院,陜西 西安 710055;3.西安長慶科技工程有限責(zé)任公司,陜西 西安 710000)
地裂縫活動引起地下結(jié)構(gòu)底部脫空是一種普遍現(xiàn)象.西安地裂縫分布廣、規(guī)模大[1],地下管廊穿越地裂縫不可避免.而管廊穿越地裂縫時,管廊結(jié)構(gòu)底部脫空對管廊結(jié)構(gòu)受力變形模式起著決定作用,且對管廊建成后的運營造成極大的安全隱患,故對管廊結(jié)構(gòu)底部脫空范圍進行計算研究十分必要.
隨著城市地下空間的開發(fā)和利用,許多學(xué)者對地下結(jié)構(gòu)穿越地裂縫開展了大量研究.范文等[2-6]進行了有關(guān)地鐵隧道的模型試驗,從不同地裂縫角度、不同隧道截面形式、不同施工方法等方面對隧道的受力變形模式、破壞模式進行了研究,結(jié)果表明:采用不同幾何相似比、不同隧道模型材料情況下,當(dāng)?shù)亓芽p活動量達到一定量值時,隧道結(jié)構(gòu)底部均有脫空現(xiàn)象出現(xiàn).胡志平等[7]通過管廊斜穿地裂縫模型試驗,認為管廊結(jié)構(gòu)產(chǎn)生扭轉(zhuǎn)的原因是由于脫空區(qū)范圍的剪力流合力不通過結(jié)構(gòu)截面的剪切中心造成的.門玉明等[8]在分析大量隧道過地裂縫模型試驗結(jié)果的基礎(chǔ)上,認為地裂縫的活動強度、隧道埋深、長度、土與隧道的剛度比等是影響隧道底部脫空區(qū)長度的主要因素,并總結(jié)了四種地鐵隧道底部脫空的計算模型.劉東燕等[9]通過將脫空區(qū)三角形范圍內(nèi)的上覆土壓力等效成一個過形心的集中力,求解箱型隧道過地裂縫的扭轉(zhuǎn)解析解.梅源[10]通過數(shù)值分析研究發(fā)現(xiàn),地裂縫沉降量達到一定值時管廊結(jié)構(gòu)底部才出現(xiàn)脫空.王啟耀[11]利用數(shù)值模擬研究了雙艙綜合管廊結(jié)構(gòu)在地裂縫活動下的受力變形特征,發(fā)現(xiàn)管廊結(jié)構(gòu)底部脫空區(qū)從上盤地裂縫處向上盤遠端發(fā)展.以上無論是地鐵隧道還是管廊方面的研究,雖然涉及到了結(jié)構(gòu)底部產(chǎn)生脫空,但大多是定性描述和分析,缺乏對管廊結(jié)構(gòu)底部脫空區(qū)范圍的定量計算研究.
現(xiàn)有研究表明,對地下結(jié)構(gòu)進行理論分析計算時,通常將其簡化為置于彈性地基上的梁[12-15],但在地裂縫作用下,地下管廊結(jié)構(gòu)底部出現(xiàn)脫空,這使得普通彈性地基梁理論的使用條件不再適用.彈性地基梁的使用條件是梁與地基連續(xù)接觸,可看作是無窮多次超靜定結(jié)構(gòu),在管廊底部脫空情況下,可將管廊與地基的接觸看作有限次超靜定結(jié)構(gòu).因此,計算管廊底部脫空范圍,就是求解有限次超靜定結(jié)構(gòu)問題.
為此,基于Euler-Bernoulli-Bousslnesq模型和鏈桿法,通過建立管廊結(jié)構(gòu)穿越地裂縫的底部脫空計算模型,給出管廊結(jié)構(gòu)底部脫空區(qū)范圍的計算方法.通過與既有管廊過地裂縫模型試驗結(jié)果進行對比分析,驗證管廊結(jié)構(gòu)底部脫空區(qū)范圍的計算方法的合理性和適用性.研究成果可為地裂縫區(qū)域管廊結(jié)構(gòu)設(shè)計提供一定參考.
1 地下管廊結(jié)構(gòu)的受力特性
已有的管廊穿越地裂縫的模型試驗結(jié)果表明[7],在上盤沉降初期,管廊上覆荷載均勻分布,隨著上盤沉降量增加,管廊頂部接觸壓力發(fā)生改變,表現(xiàn)為上盤增大,下盤減小,說明作用于地裂縫兩側(cè)管廊上的外荷載并不會隨著地裂縫的活動而變化,變化的是作用于管廊上的土壓力.管廊底部接觸壓力總體表現(xiàn)為上盤減小,下盤增大,管廊與下盤土層始終接觸;管廊變形主要表現(xiàn)為下盤底部受壓,上盤底部受拉,且靠近地裂縫處下盤管廊變形較大,遠離地裂縫處趨近于零.而上盤管廊由于土體沉降產(chǎn)生的拖拽作用,與土體發(fā)生整體沉降,在管廊底部形成局部脫空.管廊結(jié)構(gòu)變形受力示意圖如圖1所示.
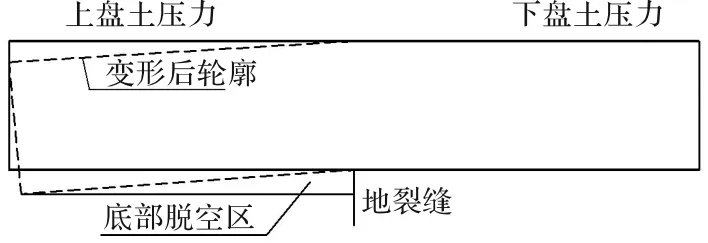
圖1 管廊結(jié)構(gòu)縱向受力圖
2 底部脫空計算模型
由管廊的受力特性可知,在管廊穿越地裂縫模型試驗中,隨著地裂縫上盤相對下降,下盤始終與地基接觸,下盤管廊在地裂縫處變形最大,遠離地裂縫變形趨近于零,因此可以將下盤土層對遠離地裂縫的管廊端部約束簡化為固定端.當(dāng)上盤沉降量達到一定值時,上盤管廊隨土體一起發(fā)生沉降變形,由于管廊與周圍土體變形的不協(xié)調(diào),在上盤管廊底部形成脫空區(qū),因此可將土層對上盤管廊端部的約束簡化為定向支座,為簡化計算,不考慮管廊頂部接觸壓力的變化,按上覆荷載q0計算,如圖2所示.

圖2 管廊結(jié)構(gòu)底部脫空計算模型
計算上盤管廊底部脫空范圍,由于下盤始終與地基接觸,故只考慮上盤管廊的情況.將位于地裂縫上盤的管廊簡化為Bousslnesq地基中的Euler-Bernoulli梁,簡稱為Euler-Bernoulli-Bousslnesq模型(EB-B模型),用鏈桿法的原理,將上盤管廊與地基接觸的部分用n個鏈桿連接,計算模型可簡化為如圖3所示,xt為管廊上盤結(jié)構(gòu)底部脫空區(qū)范圍,c為相鄰鏈桿的間距,ak為第1個鏈桿與第k個鏈桿間的間距,pn為管廊與地基相互作用力.Δ1為上盤管廊結(jié)構(gòu)端部位移,Δ2為地裂縫錯動量.
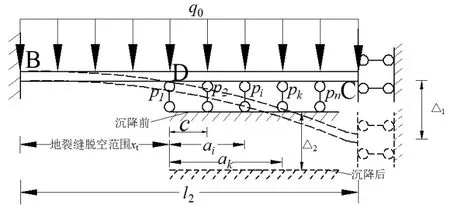
圖3 管廊結(jié)構(gòu)脫空簡化計算圖
Δ1、Δ2有這樣的關(guān)系:一是上盤管廊結(jié)構(gòu)端部位移Δ1隨地裂縫錯動量Δ2的增大有增大的趨勢,二是管廊結(jié)構(gòu)本身的抗彎剛度有阻礙管廊結(jié)構(gòu)端部位移Δ1增大的趨勢,經(jīng)過查閱數(shù)學(xué)手冊可得符合Δ1、Δ2關(guān)系的函數(shù)為雙曲正切函數(shù),經(jīng)過擬合可得符合要求的函數(shù)如圖4所示.
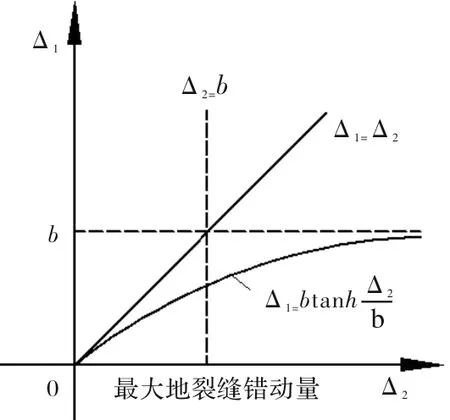
圖4 Δ1、Δ2函數(shù)關(guān)系曲線圖
則有
(1)
3 管廊結(jié)構(gòu)底部脫空范圍計算推導(dǎo)
在管廊結(jié)構(gòu)底部完全脫空前,管廊結(jié)構(gòu)與地基的接觸部分的相對位移為零,即任意鏈桿k處管廊結(jié)構(gòu)和地基的相對位移Δk=0.為求解Δk,將圖3所示超靜定結(jié)構(gòu)取作以B點為固定端的懸臂梁結(jié)構(gòu)作為基本體系,則任意鏈桿k處管廊結(jié)構(gòu)和地基的相對位移Δk由四種外荷載引起:地基反力在上盤未脫空區(qū)引起的位移Δkpi,上覆荷載在管廊結(jié)構(gòu)k點引起沿pk方向的撓度Δkq,上盤管廊結(jié)構(gòu)端部彎矩MC在管廊結(jié)構(gòu)k點引起沿pk方向的撓度ΔkMC,由上盤管廊結(jié)構(gòu)端部垂直位移Δ1在管廊結(jié)構(gòu)k點引起的撓度Δk1.則有
Δk=Δkpi+ΔkMC+Δkq+Δk1=0
(2)
現(xiàn)在對式(2)中各分項進行求解.
①Δkpi是任一點i的管廊與地基相互作用力pi在k點地基產(chǎn)生的沉降值和在管廊k點作用產(chǎn)生的撓度之和.即
(3)
式(3)中:δki為pi=1時k點地基產(chǎn)生的沉降值yki和管廊上盤結(jié)構(gòu)k點產(chǎn)生的撓度vki之和,即δki=yki+vki.
求yki可以將荷載pi=1看作以i點為基點,長度為c的區(qū)間上荷載集度為q=1/c的均布荷載,距k點r處取微段dr,微段上的荷載dp=(1/c)dr,微段荷載與基點i的距離為d=r-x,如圖5所示.

圖5 沉降計算模型
由集中力作用下的沉陷公式可得微段荷載作用下k點的相對位移為
(4)
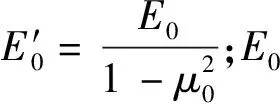
整個荷載段在k點產(chǎn)生的相對位移為
(5)
求解積分得
(6)
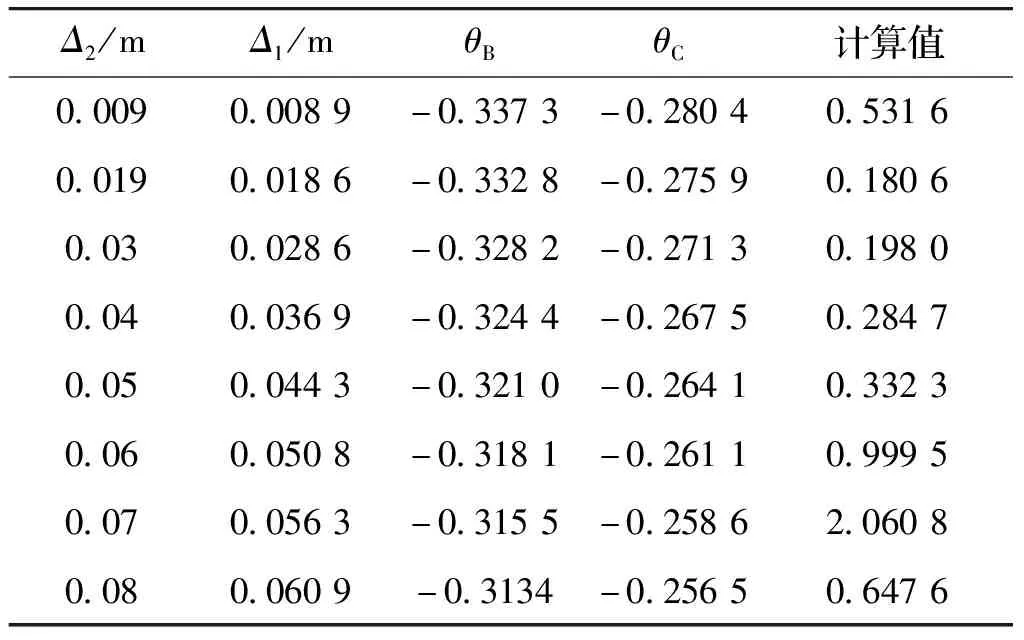
式中,F(xiàn)ki=clnc-cln(x-c)-xlnx+xln(x-c).為便于計算,對lnc,ln(x-c)展開冪級數(shù),假定0 求vki為上盤管廊結(jié)構(gòu)在地基反力pi=1作用下k點產(chǎn)生的撓度,由結(jié)構(gòu)力學(xué)撓度公式可得 (7) 則得 (8) 由式(6)、(8)可得 (9) ②求MC對上盤未脫空區(qū)管廊結(jié)構(gòu)k點產(chǎn)生的位移ΔkMC,可用結(jié)構(gòu)力學(xué)撓度積分公式計算得 (10) ③Δkq為上盤上覆荷載對未脫空區(qū)管廊結(jié)構(gòu)k點產(chǎn)生的位移,可由結(jié)構(gòu)力學(xué)撓度積分公式得 (11) 式中:MC=Rθc,θc為構(gòu)件端部相互之間的角位移;R為節(jié)點的連接剛度,R=E1I. ④上盤管廊結(jié)構(gòu)端部C點的垂直位移相對上盤管廊結(jié)構(gòu)長度是一個微量,故上盤管廊結(jié)構(gòu)端部C點的垂直位移引起未脫空區(qū)任意一點k的向下的垂直位移Δk1可直接使用幾何方法求解.得 (12) 綜上,將式(3)、(10)、(11)、(12)代入式(2),得到含xt的非線性方程組. 此外,由上盤管廊結(jié)構(gòu)滿足靜力平衡條件,對B點取矩,則有 xtp1+(xt+a2)p2+…+(xt+ak)pk+…+(xt+ an)pn-Mq+MC=MB=θBE1I (13) 式中:Mq為上盤管廊結(jié)構(gòu)上覆荷載對管廊結(jié)構(gòu)端部B點的彎矩Mq=(q0/2)l22;θB為B點的角位移. 同時,上盤管廊結(jié)構(gòu)端部還滿足端部約束條件: (14) (15) 計算管廊底部脫空范圍xt,取不同地裂縫沉降量Δ2,代入式(1),得到Δ1,將之代入式(15),得到θB,將θB代入式(14),得到θC.然后通過式(2)、(13)構(gòu)建方程組,式(2)中各項最高次冪為四次,式中存在非線性項,因此很難直接得到解析解,可利用MATLAB中的相關(guān)函數(shù)將非線性方程轉(zhuǎn)化為線性方程,即可求解得到管廊底部脫空范圍xt的值. 為了驗證管廊結(jié)構(gòu)底部脫空范圍計算方法的合理性,采用文獻[7]中地裂縫作用下1∶15管廊模型試驗與本文計算模型進行對比分析.模型試驗基本參數(shù)如下:模型管廊長5 m,管廊截面為0.56 m×0.313 m,上盤管廊長度2.175 m,模型材料的彈性模量為8.41×103MPa,模型圍巖地基由雜填土、黃土、粉質(zhì)黏土分層填筑而成,重度取為18.7 kN·m-3,彈性模量取為31.08 MPa,泊松比為0.25,地裂縫最大沉降量0.08 m,上覆土1 m,允許縫寬S=30 mm,管廊結(jié)構(gòu)截面寬度D取0.56 mm.計算時鏈桿數(shù)n取30,滿足計算精度要求.由MATLAB計算得到管廊底部脫空范圍的理論計算值,如表1所示,與模型試驗所得管廊底部脫空值進行對比,見表2. 表1 管廊結(jié)構(gòu)底部脫空范圍的理論計算值 表2 計算值與試驗值對比分析 由對比分析結(jié)果可知,管廊底部脫空范圍計算方法所得結(jié)果與模型試驗結(jié)果基本一致,最大誤差不超過-18.75%. (1)基于Euler-Bernoulli-Bousslnesq模型和鏈桿法,通過將脫空情況下的管廊轉(zhuǎn)化為有限次超靜定結(jié)構(gòu),建立了管廊結(jié)構(gòu)穿越地裂縫的底部脫空計算模型,提出了管廊結(jié)構(gòu)底部脫空范圍的計算方法. (2)通過與模型試驗進行對比分析,表明計算結(jié)果和模型試驗結(jié)果基本一致,最大誤差不超過-18.75%.說明本文提出的管廊底部脫空范圍計算方法具有一定的合理性和適用性.求解管廊底部脫空范圍后,可以通過求解有限超靜定結(jié)構(gòu),得到不同地裂縫沉降量下管廊的彎矩剪力,為地下管廊的結(jié)構(gòu)設(shè)計提供一些參考. (3)在建立計算模型時,本文將管廊簡化為Bousslnesq地基中的Euler-Bernoulli梁,只考慮了彎矩對管廊變形的影響,而忽略了剪力對其變形的影響,在后續(xù)研究中,將同時考慮彎矩和剪力對管廊變形的影響,通過對管廊在Winkler地基模型、Pasternak地基模型中簡化為Timoshenko梁的情況與本文研究進行對比分析,優(yōu)化管廊底部脫空范圍的計算方法.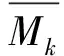
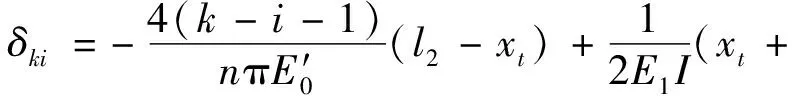

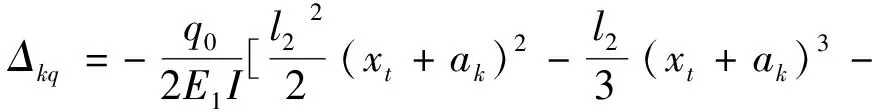


4 模型驗證

5 結(jié)果與討論

