無砟軌道底座板離縫對路橋過渡段動力學性能影響分析

羅 強 謝宏偉 李安洪 張 良 王騰飛

(1.西南交通大學， 成都 610031; 2.中鐵二院工程集團有限責任公司， 成都 610031；3.高速鐵路線路工程教育部重點實驗室， 成都 610031)

無砟軌道整體性好，維修工作量少，具有良好穩定性與耐久性，能夠適應高速度、高密度鐵路運輸的要求，在國內外高速鐵路建設中廣泛應用[1]。無砟軌道對沉降變形的適應性差且幾何形位狀態調整能力有限，控制沉降變形是路基上鋪設無砟軌道的核心問題之一。路橋過渡段剛度差異巨大，工后差異性沉降不可避免，緊鄰橋梁的路基過渡段，填筑施工時要保證橋臺的穩定與安全，作業空間小，大型壓實機具運用困難，局部可能存在壓實密度低、支承剛度小的缺陷，在列車動荷載反復作用下，路基易產生累積沉降，導致底座板部分脫空，出現離縫甚至翻漿冒泥[2]，軌道支承條件急劇劣化，加劇車輛、軌道、路基間相互作用，影響高速列車的安全、舒適運行。

過渡段處路基工后沉降映射至軌面產生幾何不平順，致使列車高速通過路基過渡段時動力學響應顯著增大[3]，為保證路基與相鄰結構間具有良好過渡性能，國內外學者對列車移動荷載下的過渡段動力響應進行了大量研究。羅強[4]運用車輛-軌道-路基耦合動力學理論，全面分析了有砟軌道條件下路橋過渡段軌面彎折變形、軌道基礎剛度變化、行車速度、車輛駛向等因素對高速鐵路路橋過渡段動力學特性的影響規律，并根據路橋過渡段動力學特性分析結果，結合已有的工程實踐經驗和研究成果，提出了針對不同速度等級的路橋過渡段結構設計與技術標準；蔡成標[5]針對無砟軌道橋隧間短路基頻繁過渡問題，分別建立了橋-路-橋、橋-路/隧、隧-路-隧3種橋隧間短路基動力學分析模型，開展了兩橋(隧)之間短路基動力學仿真分析，討論了橋隧間短路基設計參數合理取值；Wang和Markin[6]考慮過渡段剛度差異、不均勻沉降影響，并以非線性接觸單元反映不均勻沉降影響引起的有砟軌道軌枕空吊，建立了三維顯式動力有限元模型，分析了剛度與不均勻沉降對路橋過渡段動力響應的影響，并對有砟道床劣化機制進行了探討；陳虎等[7]通過現場實測，分析了板式無砟軌道路橋過渡段振動響應沿線路縱垂向的空間變化特征及與行車速度的關系。已有研究多關注有砟軌道、無砟軌道在支承條件良好或存在軌枕空吊的情況下，剛度差異及不均勻沉降引起的軌面變形而導致的過渡段動力響應的影響。而實際工程中發現無砟軌道底座板與路基接觸條件劣化往往對系統動力學性能影響較大[8]，目前對底座板離縫對無砟軌道路基動力特性的影響討論較少。

隨著列車運行速度進一步提高，路橋過渡段的動力學問題將更加顯著，尤其在無砟軌道底座板離縫情況下將更趨嚴重，引起的系統動力學問題愈加突出。為此，在列車運行速度達400 km/h時，針對橋臺與路基交界處差異沉降引起的無砟軌道底座與路基間離縫導致的過渡段服役性能劣化問題，建立車輛-軌道-路基垂向耦合動力模型，橋梁與路基過渡段考慮剛度差異，過渡段不均勻沉降引起的軌面高低不平順按 1/1 000平折角設置，通過仿真分析獲得系統動力學響應，分析離縫參數0 mm/0 m ～5 mm/5 m條件下路橋過渡段系統動力學指標變化規律，基于動力性能評估標準，提出導致底座板-路基離縫的路橋差異沉降控制建議值，討論設置剛性搭板對路橋交界處過渡性能的改善效果。

1 過渡段模型及計算方案

路橋過渡段的剛度差異、不均勻沉降、差異沉降均會產生不平順問題，列車高速通過過渡段時動力響應顯著增大。其中，路基與相鄰結構物的差異沉降將導致過渡段局部范圍的無砟軌道底座板與路基面間出現離縫而脫空，極大地削弱路基對軌道結構的支承作用，引起軌下剛度突降，劣化過渡段動力學性能。

1.1 過渡段動力學模型及參數

根據車輛-軌道耦合動力學原理[3]，考慮過渡段路基與橋臺剛度差異、不均勻沉降引起的軌面平折角不平順、差異沉降導致的底座與路基面離縫，建立車輛-軌道-路橋過渡段垂向耦合動力學分析模型(如圖1所示)，采用自橋梁朝路基方向走行的單節車輛開展動力仿真分析。

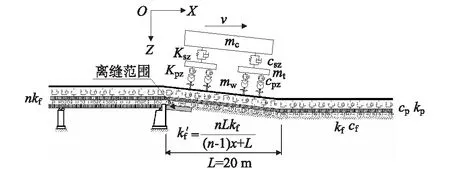
圖1 過渡段動力學耦合分析模型圖

車輛系統簡化為多剛體彈簧阻尼體系，由車體、前后轉向架及兩組輪對構成，一系、二系懸掛均采用線性彈簧-線性阻尼元件，車體、前后轉向架的沉浮與點頭運動共6個自由度，4個輪對僅考慮垂向運動，總計10個自由度。輪軌之間的法向接觸力由Herz非線性接觸理論確定。動力學仿真計算以CRH380A型車中較重的動車M2為計算車輛，并考慮車輛滿載8 t的情況，具體車輛參數如表1所示。

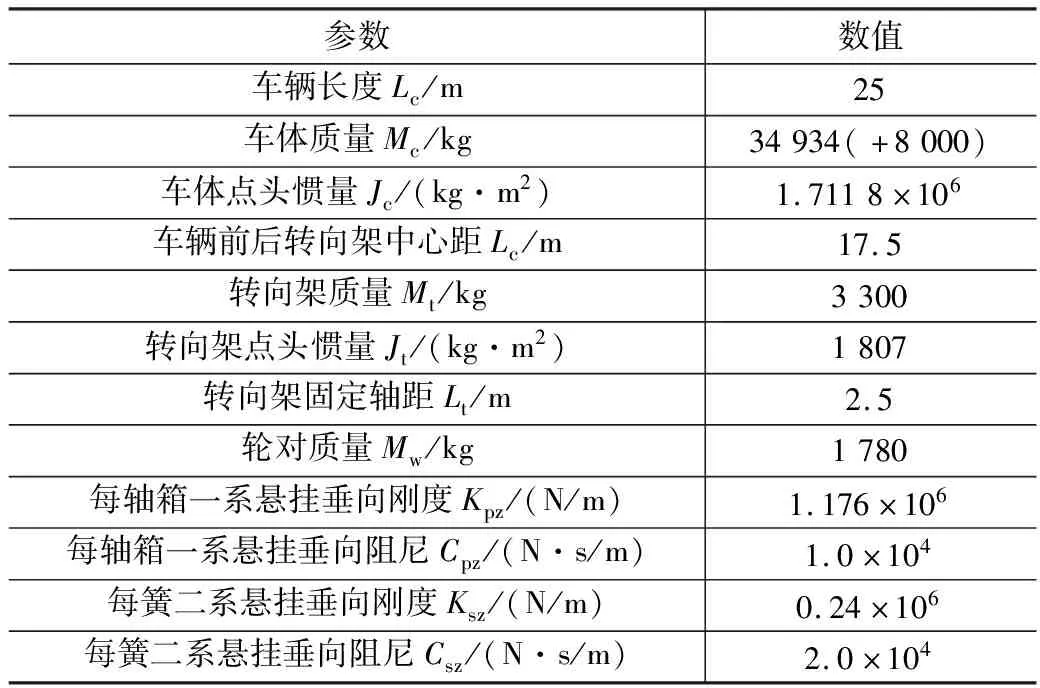
表1 CRH380A-M2車輛參數表

線路系統模型選用CRTSIII型板式無砟軌道，鋼軌由等間距分布的扣件支承于無砟軌道板之上，概化為彈性點離散支承的Bernoulli-Euler梁，考慮垂向運動自由度；將軌道板與底座板視為一個整體并抽象為黏彈性基礎(路基)上的疊合梁[9]，簡化為在等間隔分布的線性彈簧-線性阻尼支承上的無限長的單向自由板，取路基離散支承間隔與扣件間距相等以便于計算。具體計算參數如表2所示。橋梁及墩臺按底座板下的剛性基礎考慮。

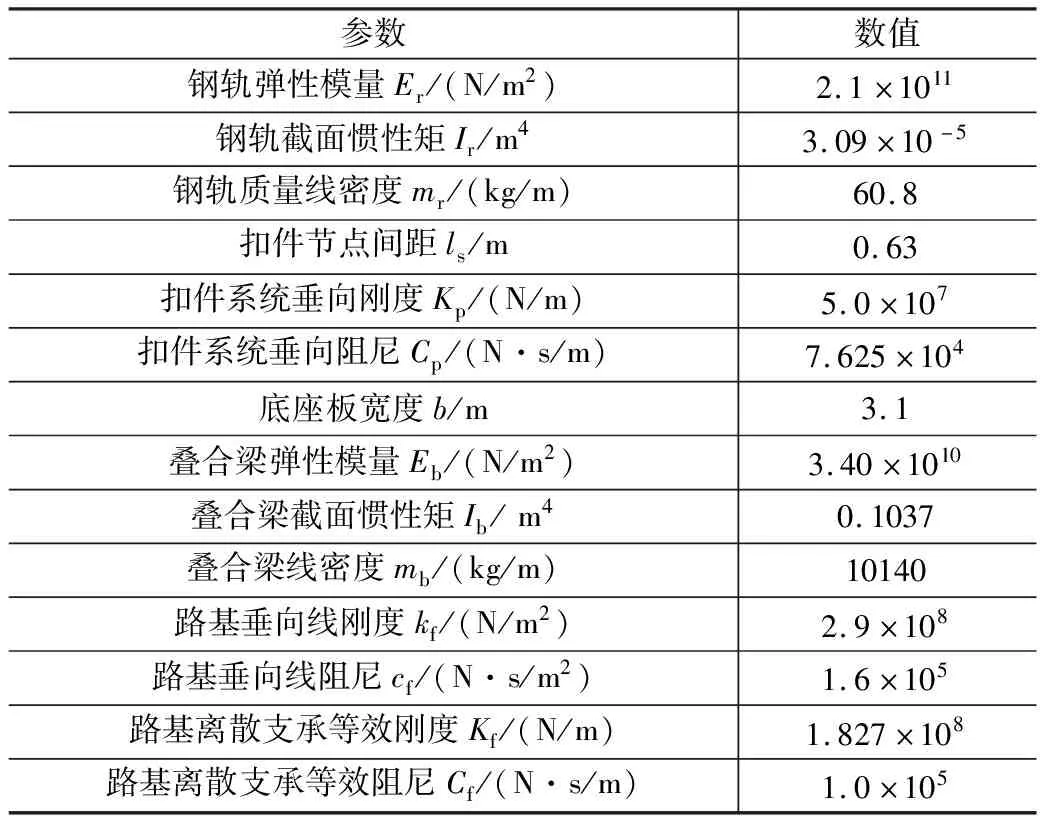
表2 CRTS-Ⅲ型板式無砟軌道模型參數表

隨著橋臺背過渡段底座支承條件不斷劣化，底座板與路基面接觸條件逐漸由無離縫的良好接觸狀態向離縫開展狀態發展。在離縫條件下，底座與路基面在振動過程中相互接觸時產生的作用力按式(1)計算。即無砟軌道底座板與路基面間離縫間隙δg較大時，離縫區域內基床完全喪失支承能力，列車荷載作用下，離縫未出現閉合；而當δg較小時，離縫區域內的基床仍可發揮部分承載能力。為便于模型計算，考慮在離縫區域長度范圍Lg內，離縫的間隙δg不變，如圖2所示。

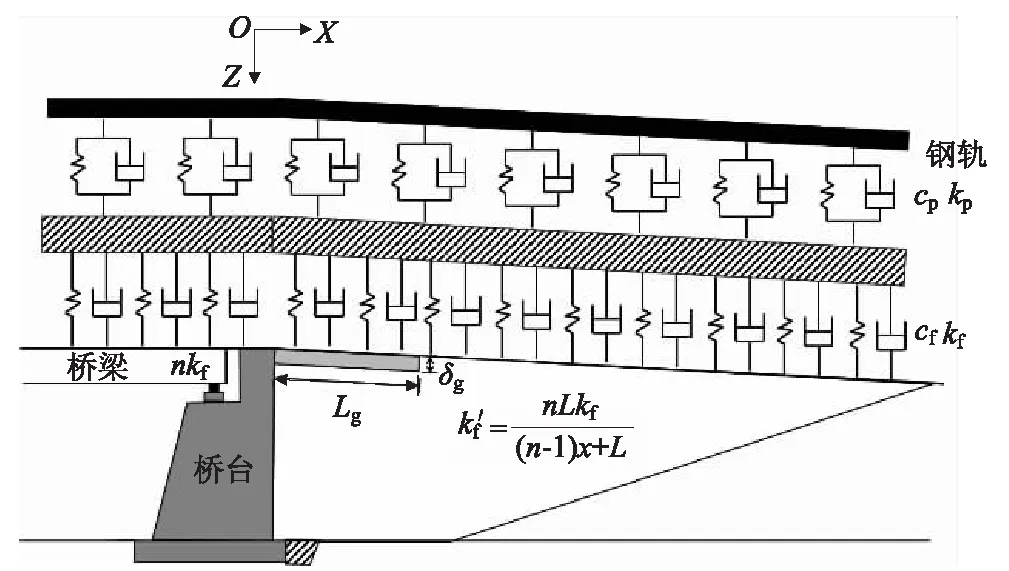
圖2 過渡段離縫區域示意圖

(1)

式中：fbf——路基與底座板之間的作用力；

kf、cf——分別為路基支承線剛度與線阻尼；

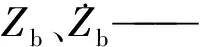
1.2 計算方案及過渡性能評價指標

過渡段部位沿線路縱向，路基與其他結構物之間剛度差異巨大，材料性質不同，導致軌道剛度的突變。同時，在列車荷載作用下，路基將產生壓密下沉，而鄰近結構物幾乎不發生沉降，因而易產生的不均勻沉降，映射至鋼軌將產生軌面幾何不平順。此外，路基與相鄰結構物交界處差異沉降將致使交界處動力作用加強，易引起無砟軌道結構與路基接觸條件劣化，進而形成底座局部脫空。三者及疊加均導致列車與線路結構相互作用增大，影響線路結構的穩定，同時加劇線路服役狀態劣化。

路橋過渡段差異沉降造成的軌面折角，日本新干線板式軌道線路規定不大于 1/1 000，德國高速鐵路無砟軌道技術標準要求不大于1/500[10]。羅強[4]通過動力學仿真分析指出，在運行速度350 km/h條件下，差異沉降引起的軌面折角滿足動力性能要求的控制值為 1.5/1 000。我國高鐵設計規范以工后階段不大于 1/1 000進行控制[10-11]，如圖3所示。

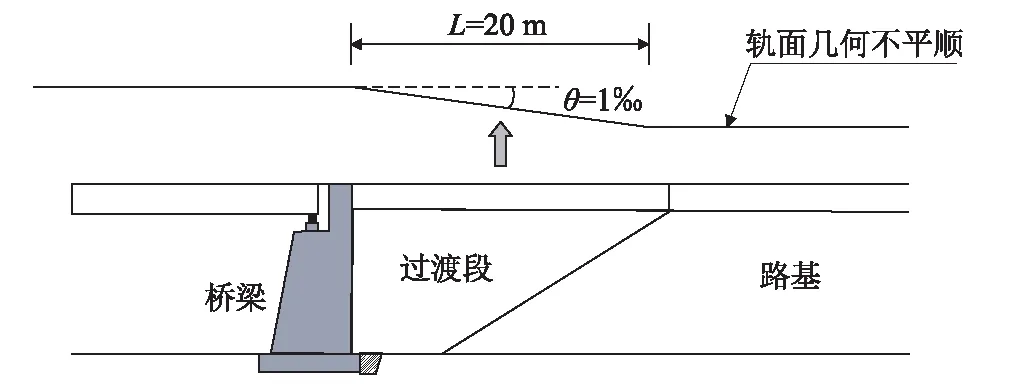
圖3 過渡段工后不均勻沉降示意圖

對于路橋結構的縱向剛度差異，混凝土結構橋梁視為剛性結構，而由松散巖土材料填筑而成的路基的支承剛度相較下有數量級的減少。路基結構采用地基系數K30控制，根據TB 10621-2014《高速鐵路設計規范》及TB 10001-2016《鐵路路基設計規范》中的高速鐵路無砟軌道路基壓實控制指標，基床表層地基系數K30≥190 MPa/m；基床底層采用粗礫土、碎石類土時K30≥150 MPa/m，當采用砂類土(粉砂除外)、細礫土時K30≥130 MPa/m；基床以下路堤為粗礫土、碎石類土時K30≥130 MPa/m，采用砂類土、細礫土時K30≥110 MPa/m。受巖土材料非線性影響，土體工作模量與應變水平有關，文獻[12]基于土體應變與模量關系曲線，分析后認為基床結構工作模量E(MPa)取值與地基系數K30(MPa/m)存在映射關系，可通過應變狀態對應的模量近似換算，基床結構的工作彈性模量約為100～200 MPa。而混凝土彈性模量為10 GPa量級，可得土質路基與相鄰混凝土結構在模量上相差約兩個數量級，即支承剛度相差約100倍。規范要求高速鐵路過渡段采用正梯形或倒梯形型式，過渡段采用級配碎石傾斜填筑，在列車荷載作用下產生彈性位移呈線性漸變，則過渡段支承剛度由橋梁端向路基端呈雙曲線形式由100kf減小至kf，如圖4所示。

圖4 過渡段支承剛度變化示意圖

過渡段動力學性能與列車運行速度緊密相關，以400 km/h條件開展列車-軌道-過渡段耦合系統的動力響應分析評價與控制限值。無砟軌道路基與橋臺交界處差異沉降限值不超過5 mm[10]，并按軌面折角 1/1 000的最不利條件[11]，確定離縫間隙高度與離縫區域長度的對應關系。

過渡段長度按20 m取值，橋臺與路基的支承剛度比值為100倍的條件下，以過渡段路基工后不均勻沉降引起的軌面折角 1/1 000、底座與路基良好接觸(不出現離縫)的工況I為基準，考慮底座板離縫間隙高度分別為1 mm、2 mm、3 mm、4 mm、5 mm(對應離縫范圍分別為1 m、2 m、3 m、4 m、5 m)，分析離縫參數對路橋過渡段動力學性能影響。此外，對離縫間隙高度5 mm、離縫長度5 m的極限最不利情況，考慮在橋臺后方設置長×寬×厚為8 m×4.3 m×0.6 m的剛性混凝土過渡搭板形式(如圖5所示)，研究過渡搭板對過渡段系統動力響應性能的改善作用。7種計算工況如表3所示。

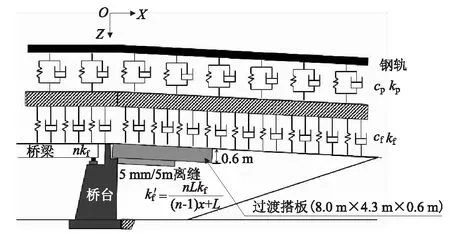
圖5 過渡搭板設置示意圖

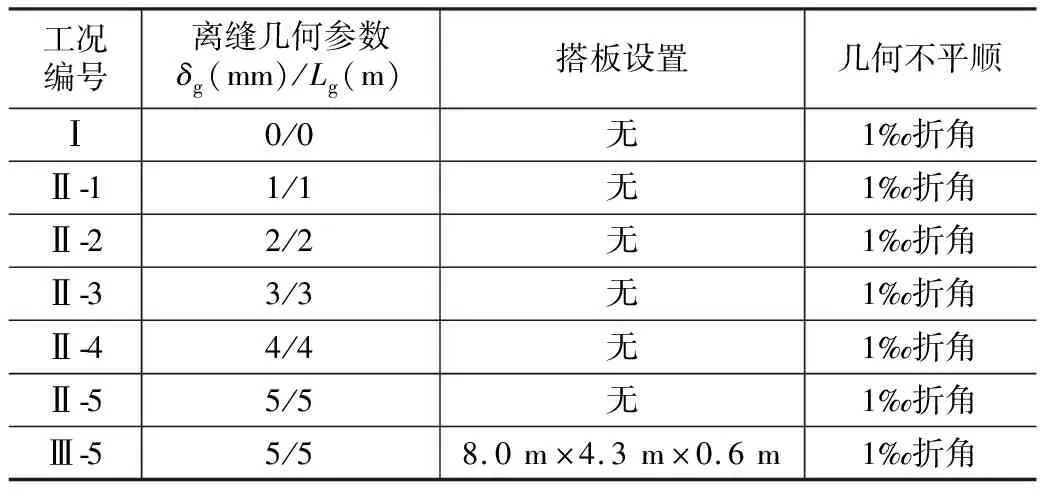
表3 過渡段耦合動力學計算方案表

表4 過渡段動力學性能評判標準表[13]

2 動力學響應數據及分析

采用過渡段系統耦合動力學分析模型，考慮土質路基與橋臺間剛度100倍剛度差異與由過渡段不均勻沉降引起的平折角為 1/1 000的軌面不平順，針對離縫參數為0 mm/0 m～5 mm/5 m與離縫間隙高度為5 mm且設置過渡搭板的共計7種工況分別進行仿真分析。其中，典型工況Ⅱ-1(1 mm/1 m離縫)、工況Ⅱ-5(5 mm/5 m離縫)、工況Ⅲ-5(5 mm/5 m離縫且設置搭板)的動力學響應曲線分別如圖6與圖7所示。受路基不均勻沉降映射至軌面產生的幾何不平順影響，輪軌力P、鋼軌位移Zr、底座板位移Zb、路基面應力σd在橋臺與過渡段及過渡段與路基交界處附近均存在明顯波動，動力作用增強，而車體加速度ac沿縱向波動不顯著。受線下基礎剛度差異的影響，橋臺處鋼軌位移Zr、底座板垂向位移Zb小于路基處，且在過渡段范圍內近似線性變化。同時，由于路橋交界處附近底座板部分脫空影響，離縫范圍內輪軌力P因“卸載”效應而減小，路基面應力σd在產生離縫的交界處出現明顯增大，這是底座板與路基面之間支承力缺失，繼而引發緊鄰路基應力集中。設置過渡搭板后，由路橋交界處的差異沉降導致的離縫引起的動力響應顯著減小，離縫導致的支承剛度缺失由搭板的抗彎剛度有效補充，過渡段動力性能明顯改善。

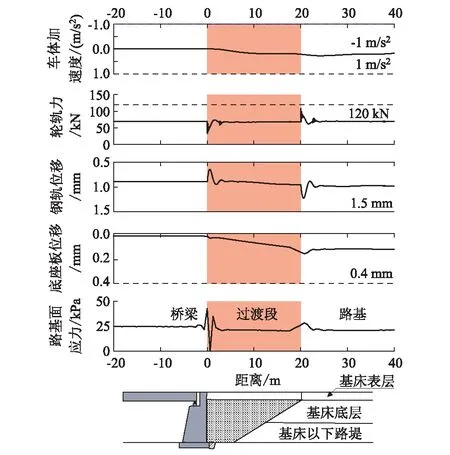
圖6 過渡段典型動力學響應曲線圖(工況Ⅱ-1)

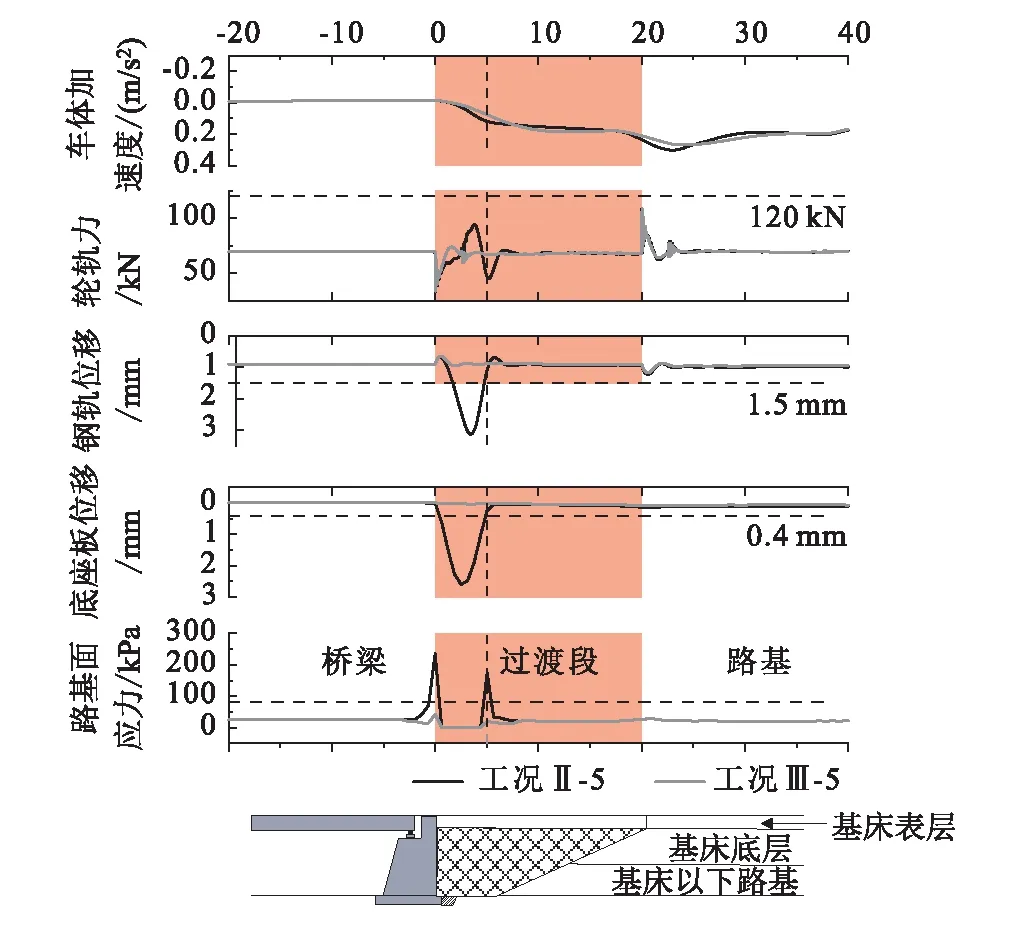
圖7 過渡段典型動力學響應曲線圖(工況Ⅱ-5與工況Ⅲ-5)

定義限值比R為表5中動力響應最大值Remax與表4中控制值Rec的之比，如式(2)所示。限值比R反映各動力響應指標與對應控制值的相對值，便于不同指標相互對比。

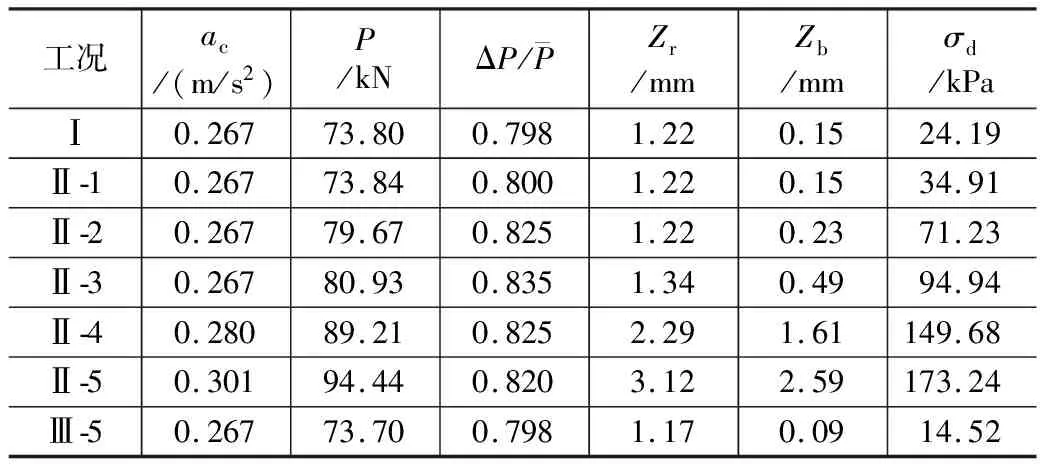
表5 動力響應指標最大值表

(2)

在底座板與路基良好接觸條件下，同時考慮線下基礎剛度差異與路基不均勻沉降引起的軌面幾何不平順的工況I，各項動力響應指標均未超過控制值(限值R≤1)。這表明若路橋差異沉降控制良好，底座與路基間未形成離縫，即使在路橋剛度差異與不均勻沉降引起的軌面不平順不利條件共同影響下，路橋過渡段仍具有良好的動力性能，可滿足線路安全服役要求。

當底座板與路基接觸條件劣化，橋臺背與路基差異沉降將導致底座板產生離縫，隨著離隙范圍擴展，過渡段動力響應指標呈加速增大趨勢，如圖8所示。其中，鋼軌位移、底座板位移、路基面應力顯著升高，車體加速度與輪軌力增加幅度相對較小。當鋼軌位移、底座板位移、路基面應力接近規范限值時，離縫參數整體介于2 mm/2 m～3 mm/3 m之間，即路橋交界處的工后差異沉降可按2～3 mm控制。

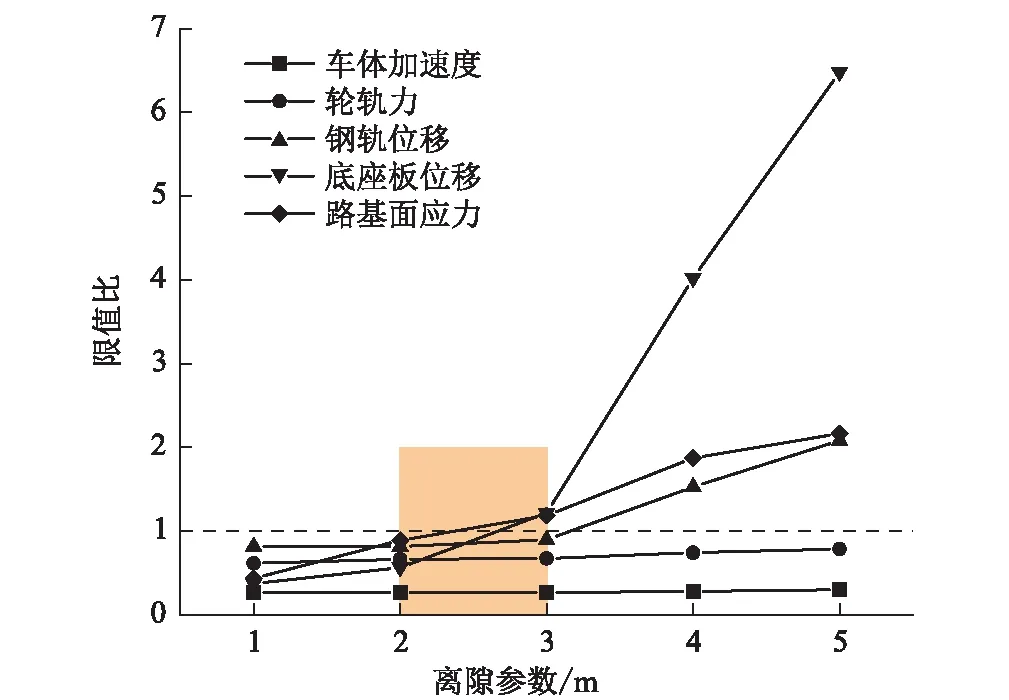
圖8 離縫參數對過渡段動力響應影響圖

在離縫參數均為5 mm/5 m條件下，對比設置搭板的工況Ⅲ-5與未設置搭板的工況Ⅱ-5，發現設置搭板能有效降低動力響應，鋼軌最大位移由3.12 mm減小至1.17 mm，底座板最大位移由2.59 mm減至0.09 mm，路基面最大動應力由173.24 kPa大幅減小至14.52 kPa(如表5與圖9所示)。過渡段設置搭板后，各項動力響應指標均降至限制值以下，在路橋過渡段設置搭板能夠顯著改善路基受力狀態，有效提升過渡段服役性能。

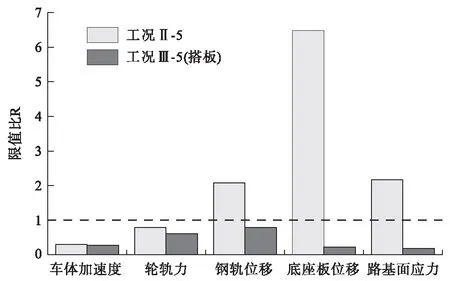
圖9 設置搭板對過渡段動力響應影響圖

3 結論

針對路基與橋臺交界處產生的工后差異沉降導致軌道板底脫空形成離隙，過渡段平順性劣化問題，開展了車輛-無砟軌道-路橋過渡段耦合動力學仿真分析，討論了在支承剛度和不均勻沉降引起的不平順基礎上，橋臺背附近無砟軌道板底局部離縫對過渡段動力學性能的影響及設置混凝土過渡搭板的改善效果，得出以下主要結論：

(1)受橋臺背路基局部沉陷影響的無砟軌道底座板接觸狀態，對高速鐵路路橋過渡段的動力學性能影響顯著。計算表明，無砟軌道處于良好接觸狀態下的過渡段性能滿足高速行車的要求，但隨著無砟軌道板底離隙范圍的擴展，過渡段線路結構的動力學響應指標呈加速劣化趨勢。

(2)以400 km/h運行速度下車體垂向加速度、輪載力及減載率、鋼軌與底座板動位移及路基面動應力為評價指標，依據高速鐵路無砟軌道與路基結構的動態驗收技術標準，路橋交界處的工后差異沉降應由現行設計規范不應大于5 mm調整為2～3 mm。

(3)在過渡段的橋臺背鋪設鋼筋混凝土搭板，是解決結構間差異沉降導致無砟軌道板底離縫、進而引發過渡段性能嚴重退化的有效措施。分析表明，在路橋之間設置一塊長×寬×厚為8 m×4.3 m×0.6 m的C35鋼筋混凝土搭板，可保證過渡段在路橋交界處發生5 mm差異沉降下仍具有良好性能。