基于SAPSO-ELM的瓦斯涌出量分源預測及應用

任海峰，嚴由吉，吳青海

(西安科技大學 安全科學與工程學院，陜西 西安 710054)

為了有效防止瓦斯事故的發生，煤礦瓦斯涌出量的準確預測對安全管理有十分重要的作用[1]。傳統的瓦斯涌出量預測方法有礦山統計法、分源預測法等[2]。由于煤層地質條件和自然因素的差異，傳統的瓦斯涌出量預測法在實際應用上存在一定的局限性。國內外學者在傳統預測方法的基礎上不斷進行優化，如徐剛等[3]提出了基于因子分析法與BP神經網絡的工作面瓦斯涌出量預測方法。于健等[4]提出了以核熵成分分析與粒子群支持向量機相結合的預測模型。李振興等[5]采用BP神經網絡來實現瓦斯涌出量的預測，通過對預測模型的訓練及仿真，對BP算法進行了改進優化。溫廷新等[6]建立了基于PSOBP-AdaBoost 算法的瓦斯涌出量分源預測模型。謝國民等[7]提出一種多元混沌時間序列的加權極端學習機瓦斯涌出量預測模型。P.Booth等[8]研究了瓦斯排放預測局限性的改進方法，提高了瓦斯涌出量預測的精度。M.Borowski等[9]基于多層感知網絡MLP建立瓦斯涌出量預測模型并對煤礦瓦斯涌出量進行預測。WANG Yan等[10]提出采用灰色系統建模預測瓦斯涌出量。

以上研究在一定程度上提高了預測精度，但瓦斯涌出量具有影響因素多、非線性等特征，且影響因素之間存在多重相關性，會增加預測模型的復雜性，這就導致不同地質條件下瓦斯涌出量預測結果的準確性和預測精度的提高受到了一定的限制。

為了更加精確和高效地預測瓦斯涌出量，在分源預測的理論基礎上，采用主成分分析法，在保留原始變量主要信息的基礎上對各涌出源的瓦斯涌出量影響因素進行降維；針對極限學習機(ELM)存在的輸入權值矩陣與隱含層閾值隨機生成的問題，利用模擬退火粒子群算法(SAPSO)對極限學習機的參數尋優，建立基于SAPSO-ELM的瓦斯涌出量分源預測模型，對開采層、鄰近層、采空區3個涌出源進行預測，再將涌出源的預測結果進行疊加，得到最終的預測結果。

1 主成分降維

主成分分析法是一種降維的方法，在保留主要信息的原則下，對多影響因素數據進行最佳綜合簡化的多元統計方法[11]。主成分是原始變量的線性組合，且主成分之間互不相關，這樣既不丟失原始數據的主要信息，又能夠提高分析精度[12]。

對于n個樣本，每個樣本有p個指標。設Xi=（xi1,xi2,…,xip），則樣本數據可表示成

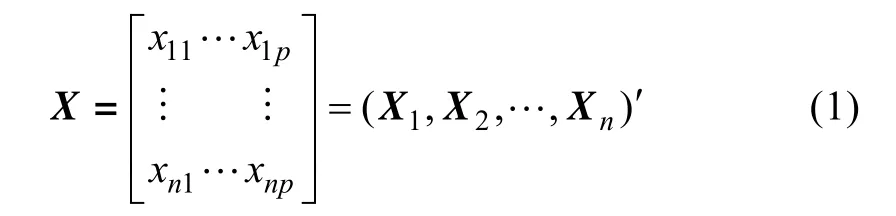
對矩陣X進行線性變換，得到新的綜合變量，F1、F2、…、Fp為原始變量x1、x2、…、xp的第1，第2、…、第p主成分。

主成分系數λij需滿足以下條件：

①各個主成分互不相關；

②主成分方差大小為F1＞F2＞…＞Fp；

③各個主成分里的系數平方和為1。

采用SPSS軟件進行主成分分析[13]，基本步驟如下。

①數據預處理。瓦斯涌出量的各影響因素之間的數量級和量綱不同，數據之間存在差異性，在主成分分析之前，需要對數據進行標準化處理。

②主成分分析計算。由SPSS中的因子分析功能獲得總方差解釋表、因子載荷矩陣等結果，最后按照上述原理進行主成分分析計算。

③確定主成分。根據累計貢獻率來選取主成分，一般規定，累計貢獻率＞80%時，選取的主成分即滿足要求。

④統計主成分得分。通過主成分系數矩陣可以列出主成分的表達式，再將標準化后的數值代入主成分表達式計算出主成分得分。主成分得分即為降維后的數據。

⑤因子旋轉。對因子載荷矩陣進行因子旋轉，根據旋轉后的主成分載荷矩陣可以看出每一主成分所代表的原始變量的信息。

2 預測模型的構建

2.1 極限學習機

極限學習機(ELM)是一種新型的單隱層前向型神經網絡。其通過隨機方式生成隱含層輸入權值和偏差，只需要設定網絡結構，便可僅通過一步計算得到網絡的輸出權值，具有較強的非線性擬合能力，計算能力快，而且泛化能力強[14]。根據傳統神經網絡最佳隱含層節點數的設定原則進行多次參數調試，當預測結果最優時確定最佳隱含層節點數[15]。

ELM算法主要步驟為：

①隱含層神經元個數的設定，輸入層與隱含層間連接權值ω及隱含層神經元閾值b的隨機生成；

②選擇無限可微的隱含層神經元的激活函數，計算出隱含層輸出矩陣H；

式中：H+為隱含層輸出矩陣H的Moore-Penrose廣義逆矩陣；R′為網絡輸出矩陣的轉置。

2.2 模擬退火粒子群算法

粒子群優化算法(Particle Swarm Optimization，PSO)是一種基于群體智能優化算法，采用實數求解，且需要調整的參數較少[16]，是一種通用的全局搜索算法。針對粒子群優化算法(PSO)容易陷入局部極值點、進化后期收斂慢的問題，引入模擬退火思想。模擬退火算法(Simulated Annea-ling，簡稱SA)用熱力學系統來模擬求解優化問題，搜索初期SA溫度較高，具有較強的全局搜索能力，隨迭代的進行，SA溫度逐漸降低，進行精細搜索，在搜索過程中利用具有概率突跳特性的 Metropolis 抽樣準則，能夠有效地避免陷入局部極小解[17]。

2.3 SAPSO-ELM算法設計

SAPSO算法以粒子群算法為主流程，在其中引入固體退火原理，并結合自適應慣性權重調整策略和群體適應度方差來平衡PSO算法的全局和局部搜索能力[18]。針對ELM隨機產生輸入權值及隱含層閾值的問題，由于SAPSO具有全局搜索和跳出局部最優解的能力，采用SAPSO對ELM的輸入權值與隱含層閾值動態尋優，使ELM只需要較少的隱含層神經元數就能達到較好的預測效果，從而避免算法容易陷入局部極值點，提高后期算法的收斂速度和精度及網絡的泛化性[19]。利用 SAPSO 算法優化 ELM 的輸入層權值(慣性權重因子)ω及隱含層閾值b，具體步驟如下。

第1步：樣本歸一化處理；設置隱藏節點數和神經元個數，選中并激活函數。

第2步：模型參數初始化。參數包括起始溫度T、降溫速度α、學習因子c1和c2、慣性權重因子ω、目標空間所有粒子的速度v和位置p，設置迭代終止條件等。

第3步：載入標準化后的訓練樣本，按照訓練樣本誤差的均方差計算適應度函數，見式(3)。

式中：N為樣本個數；yi、yi′分別為第i個樣本的實際值和預測值。

第4步：每次迭代中，產生新解x并計算各個粒子的適應度函數值，按式(4)計算其增量，其中f（x）為評價函數。

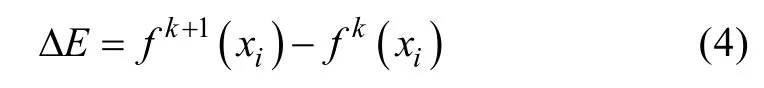
式中：k為當前迭代次數；f(x)為評價函數。

第5步：若ΔE＜0，則接受x作為新的當前解，根據式(6)對系統溫度進行更新；否則溫度不變，經過迭代T逐漸減小并趨于0。

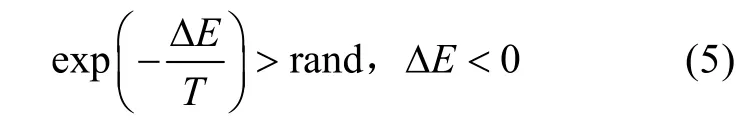
式中：rand為一種產生隨機數的函數。

第6步：按照式(7)－式(8)更新粒子的速度和位置，同時按照式(9)自適應調整慣性權重因子ω，并計算各粒子的適應度函數。找出所有粒子當前最優位置pid和全局最優位置pgd。

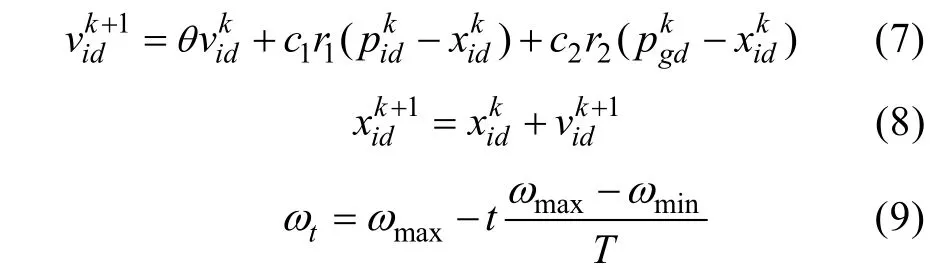
式中：i=1,2,3,…,M為粒子編號；d=1,2,3,…,D為維度；r1和r2為區間［0,1］的隨機數；t為時間；xid和vid分別為粒子i在第d維的位置和速度。

第7步：判斷系統是否達到迭代終止條件。若達到，停止迭代，此時的pgd即為最優(ω,b)，將其代入ELM網格中進行訓練，計算輸出權重β和實際輸出矩陣R；否則轉至第3步繼續迭代。

運用Matlab軟件對SAPSO-ELM模型和ELM模型進行訓練，其均方誤差曲線如圖1所示。由圖1可看出，隨迭代次數增加，SAPSO-ELM模型在80次即達到收斂，而ELM模型在100次之后才達到收斂。SAPSO-ELM模型的均方誤差下降速度比較快，在最短的次數內到達收斂精度附近，比較而言，SAPSO-ELM模型尋優速度更快且收斂精度更高，明顯提高了ELM模型的學習效率。

利用SAPSO算法優化ELM所建立的SAPSOELM模型，避免了ELM參數隨機生成導致的網絡不穩定以及PSO在尋優過程中易陷入局部極小值問題。與原始ELM模型相比SAPSO-ELM模型具有算法穩定性和預測精度更高的優勢。

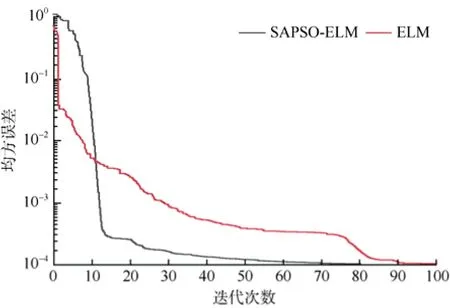
圖1 均方誤差曲線Fig.1 Mean square error curves

2.4 預測模型的構建步驟

根據上述理論分析及SAPSO-ELM算法可建立瓦斯涌出量的預測模型，模型的具體建立過程如下。

第一步：依據分源預測理論確定瓦斯涌出來源并選取影響因素；

第二步：采用主成分分析法選取預測指標，得到降維后的數據集；

第三步：劃分訓練集、測試集，輸入樣本數據；

第四步：SAPSO-ELM算法參數的設置；

第五步：先得到各涌出源預測結果再進行疊加得到回采工作面預測結果。

3 應用及分析

3.1 瓦斯涌出量影響因素選取

根據分源預測理論，回采工作面瓦斯的主要來源為開采層、鄰近層、采空區[20]。選取影響瓦斯涌出量的各個來源的變量因素，影響因素用x1，x2，…，x9來表示，其對應關系見表1，其中，該煤礦回采工作面頂板管理方式均為全部垮落法，因此，可忽略頂板管理因素[21]。

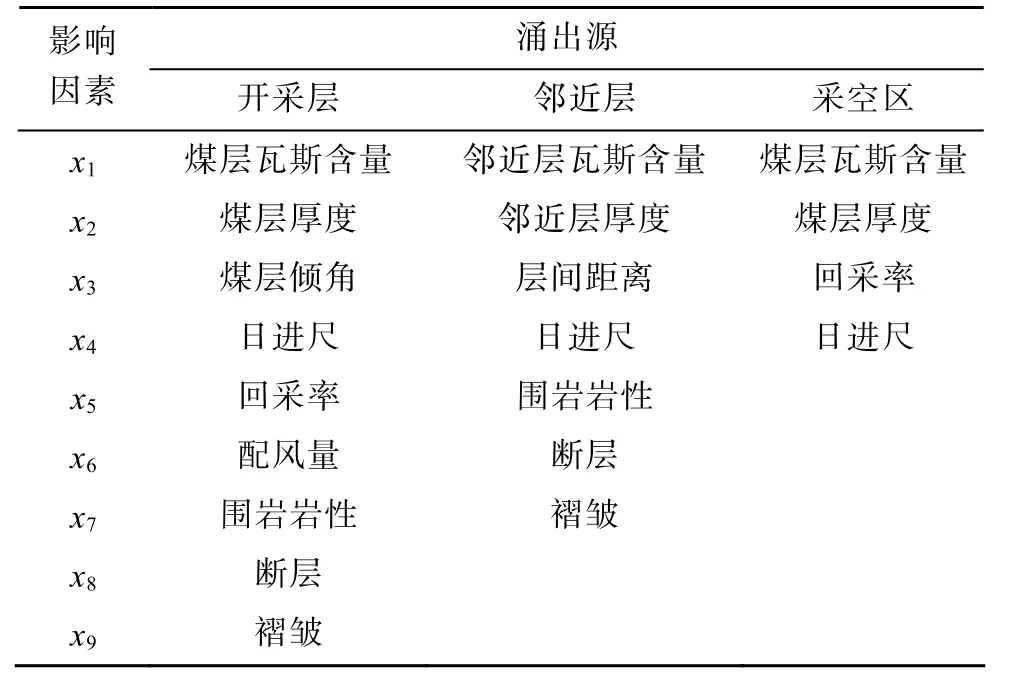
表1 瓦斯涌出來源及其影響因素Table 1 Source of gas emission and its influencing factors

針對煤礦瓦斯涌出量影響因素分析，根據神經網絡的輸入輸出向量構成，將新疆某煤礦回采工作面現場實測的分源瓦斯涌出量及其各影響因素的指標形成原始數據集，以便進行網絡訓練，為了更符合實際情況，根據數量化理論將難以量化的圍巖巖性、斷層、褶皺等定性影響因素轉化為二分變量進而量化，即以“0.5”和“1”表示某個定性指標的“不存在”和“存在”。原始數據集見表2。

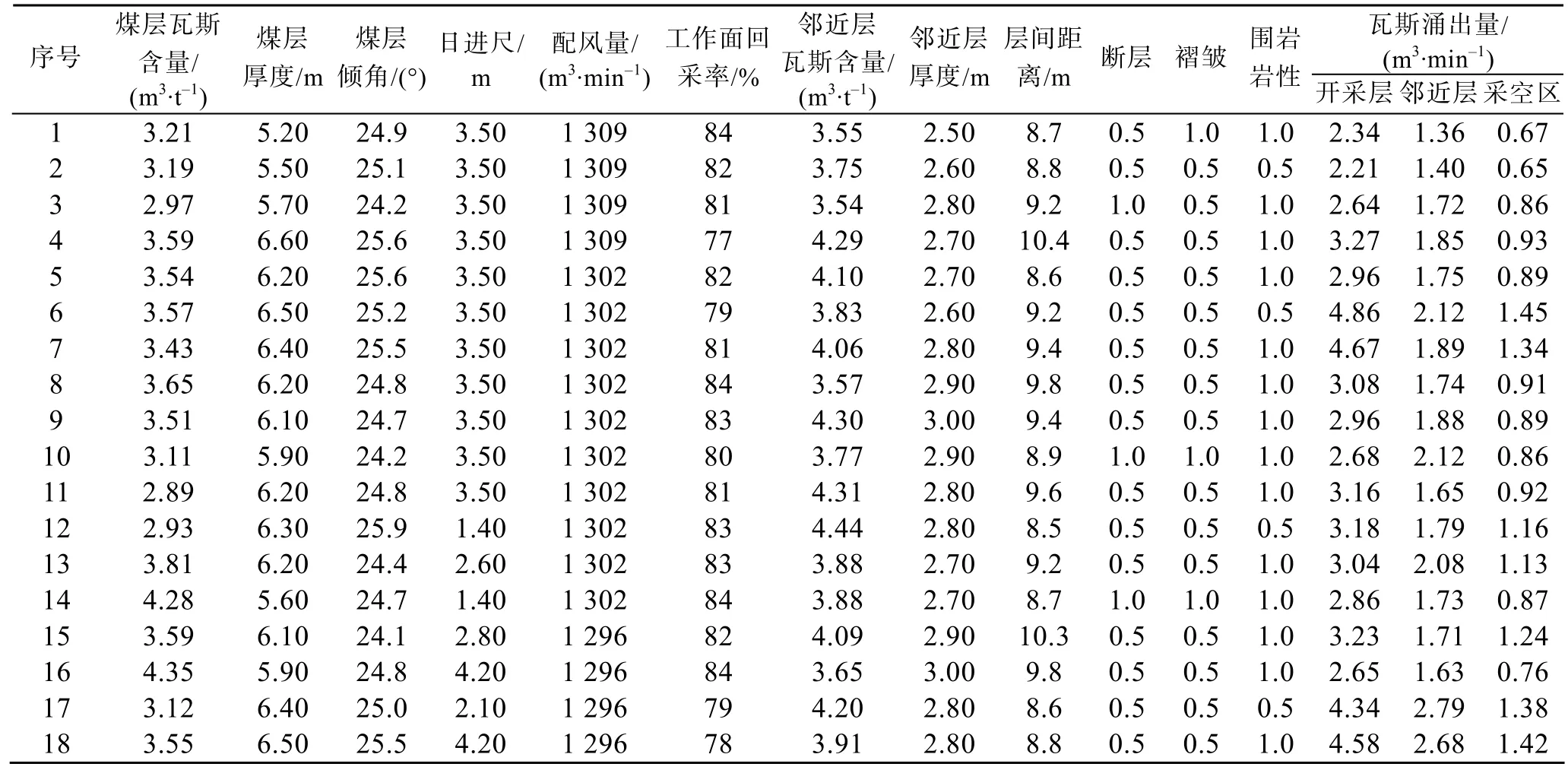
表2 瓦斯涌出量及各影響因素原始數據統計Table 2 Raw data statistics of gas emission and various influencing factors

3.2 影響因素的處理及主成分的選取

對各影響因素原始數據采用SPSS軟件進行歸一化處理，以消除影響因素之間的差異性。再對歸一化后的數據進行因子分析，分別得到開采層、鄰近層、采空區的總方差解釋圖，以此來選擇主成分的個數。各個涌出源的累計貢獻率如圖2所示。

依據圖2累計貢獻率來選取主成分，在保留大部分原始信息的前提下，分別選取開采層5個主成分、鄰近層4個主成分、采空區2個主成分；其累計貢獻率分別是86.709%、83.403%、76.235%。依據選取的主成分以及因子載荷矩陣計算主成分得分系數矩陣，其計算方法是用因子載荷矩陣中每個主成分的數值除以對應主成分的特征根的平方根，依次得到各個主成分中每個變量的系數，結果見表3。

圖2 主成分累計貢獻率Fig.2 Cumulative contribution rate of principal components

表3 主成分得分系數Table 3 Principal components score coefficient

3.3 主成分得分及解釋

通過主成分得分系數可以寫出主成分表達式，從而計算出主成分得分，即降維后的數據，由主成分得分可知，對于開采層、鄰近層、采空區3個瓦斯涌出來源，其影響因素由原來的9維、7維、4維降到5維、4維、2維。將前12組數據形成訓練集，后6組形成測試集，檢驗SAPSOELM模型的預測效果。通過旋轉因子載荷矩陣的方法，從而得到旋轉后的主成分載荷矩陣，結果見表4。

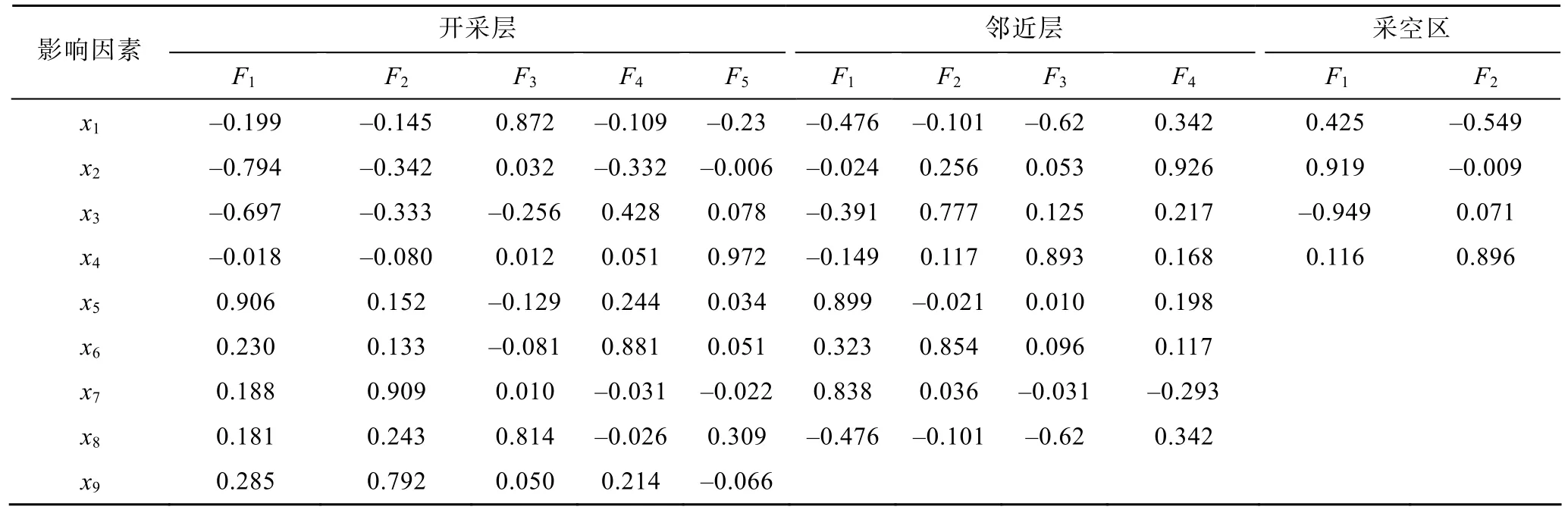
表4 主成分載荷Table 4 Principal components load

忽略每個主成分中不相關的影響因素，可以更好地反映每個主成分所代表的原始信息。對于開采層：第一主成分主要有煤層傾角、煤層厚度、回采率影響因素；第二主成分主要有斷層、褶皺因素；第三主成分主要有煤層瓦斯含量、圍巖巖性因素；第四主成分主要有煤層傾角、配風量；第五主成分主要有日進尺影響因素。對于鄰近層：第一主成分主要有鄰近層瓦斯含量、斷層、褶皺影響因素；第二主成分主要有層間距離、圍巖巖性因素；第三主成分主要有日進尺因素；第四主成分主要有鄰近層厚度影響因素。對于采空區：第一主成分主要有煤層厚度、回采率影響因素；第二主成分主要有煤層瓦斯含量、日進尺影響因素。

3.4 模型預測結果分析

將各涌出源主成分得分的1－12組作為訓練集，13－18組作為測試集，使用SAPSO-ELM模型對測試集進行仿真計算，SAPSO-ELM模型的預測結果見表5。結果顯示，SAPSO-ELM模型的瓦斯涌出量預測值與新疆某煤礦回采工作面實際瓦斯涌出量的平均相對誤差為3.47%，說明訓練好的SAPSO-ELM模型具有較好的預測精度。

為了驗證SAPSO-ELM模型對于礦井的普適性和應用價值，另以陜西某煤礦為例，收集6組瓦斯涌出量數據作為驗證樣本，分別使用訓練好的SAPSO-ELM模型、ELM模型對驗證樣本進行仿真計算，兩種模型的參數設置保持一致，SAPSO-ELM模型與ELM模型以及陜西某煤礦回采工作面瓦斯涌出量實際值的對照圖如圖3所示，SAPSO-ELM模型的瓦斯涌出量預測曲線更貼近瓦斯涌出量實際曲線。2種模型與實際值的相對誤差對比圖如圖4所示，SAPSO-ELM模型的瓦斯涌出量預測值與該煤礦回采工作面實際瓦斯涌出量的平均相對誤差為3.45%，而ELM模型的瓦斯涌出量預測值與該煤礦回采工作面實際瓦斯涌出量的平均相對誤差為8.81%，說明SAPSO-ELM模型的預測精度較高。而且SAPSO-ELM模型曲線的趨勢要平緩，說明主成分分析對數據起到了降維效果，降低了模型預測的復雜度，提高了瓦斯涌出量預測的可靠性和穩定性。

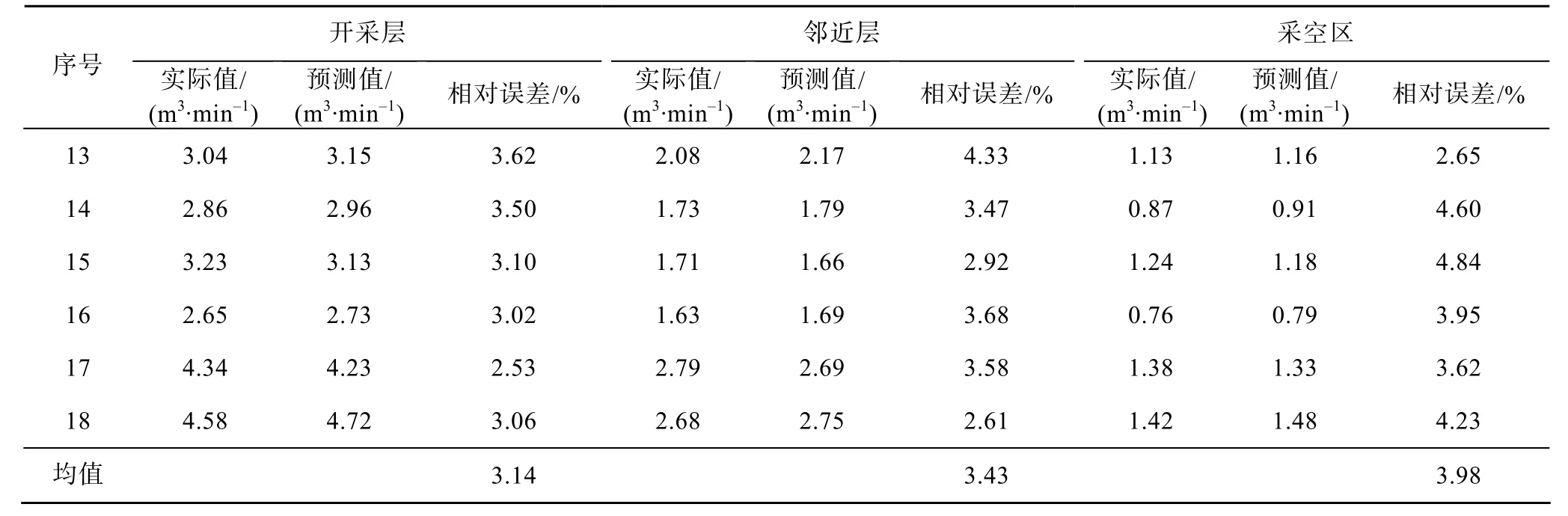
表5 測試樣本瓦斯涌出量預測結果Table 5 Prediction results of gas emission of test samples

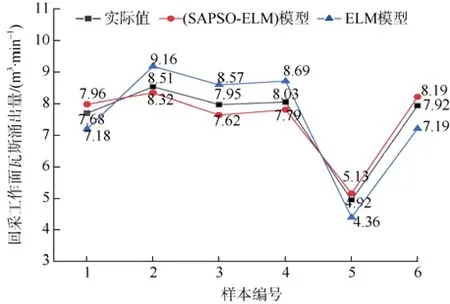
圖3 預測值與實際值對照Fig.3 Comparison of the predicted and actual values

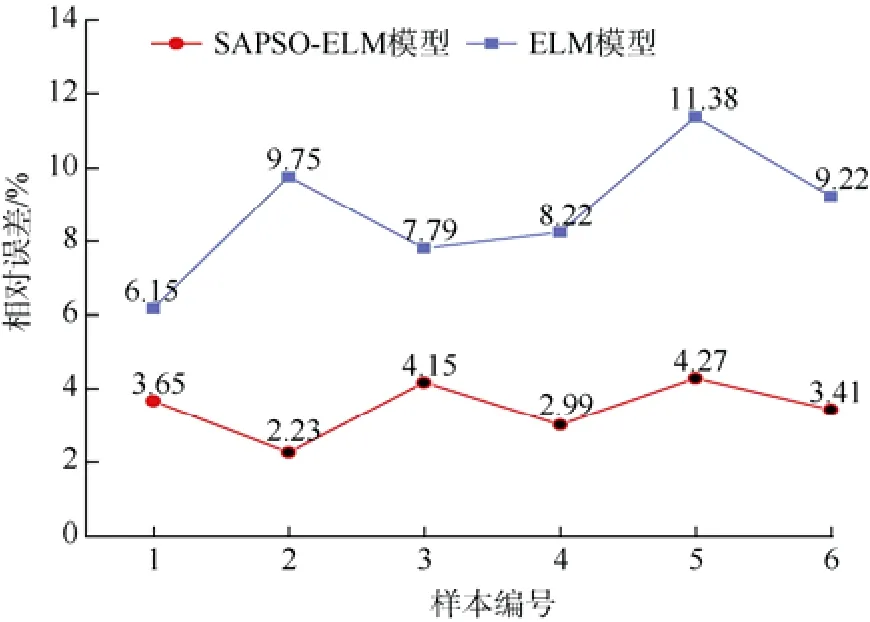
圖4 ELM、SAPSO-ELM模型預測值較實際值誤差對比Fig.4 Comparison of the error between the predicted values of ELM and SAPSO-ELM model compared to the actual values

4 結論

a.將分源預測理論和基于智能算法的預測方法相結合，建立了基于SAPSO-ELM的瓦斯涌出量分源預測模型。采用主成分分析法對開采層、鄰近層、采空區3個瓦斯涌出來源的影響因素數據進行降維，提高了瓦斯涌出量預測的可靠性和穩定性。

b.針對極限學習機(ELM)存在的輸入權值矩陣與隱含層閾值隨機生成的問題，利用模擬退火粒子群算法(SAPO-ELM)對極限學習機的參數進行尋優，使SAPO-ELM模型尋優速度更快且收斂精度更高。

c.針對陜西某煤礦回采工作面，應用訓練好的SAPSO-ELM瓦斯涌出量分源預測模型進行瓦斯涌出量預測，預測結果與該煤礦回采工作面實際瓦斯涌出量之間的平均相對誤差為3.45%，ELM模型的預測結果與該煤礦回采工作面實際瓦斯涌出量之間的平均相對誤差為8.81%。表明采用主成分分析法與分源預測理論相結合的方法構建的SAPSO-ELM預測模型可進一步提高瓦斯涌出量的預測精度。