空間繩網有控展開方法及優化

司驥躍，龐兆君，杜忠華，馮廣斌

(南京理工大學機械工程學院，南京210094)

0 引 言

面對日益嚴峻的空間環境問題，空間繩網抓捕技術被認為是一種有前景的空間碎片主動清除技術[1-2]。最常見的空間繩網抓捕系統通過母平臺發射若干個牽引體帶動折疊的空間繩網展開，繩網與母平臺之間有拖曳繩連接。之后空間繩網朝向抓捕目標飛行并與目標接觸，在收口裝置的作用下對目標形成可靠包裹。最終由母平臺通過拖曳繩將目標拖離至墳墓軌道，實現空間碎片主動清理[3]。

本文重點研究空間繩網展開階段的性能優化問題。由于空間實驗高難度和高成本的制約，現階段人們主要通過數值仿真的方法對處于空間環境中的繩網展開過程進行研究。空間繩網的動力學建模方法主要有彈簧質點法[4-6]和絕對節點坐標法[7-8]。盡管有研究表明描述繩網內部節點的運動時，絕對節點坐標法相比彈簧質點法存在一些優勢。但是由于絕對節點坐標法的單元具有更多的自由度，其計算效率遠低于彈簧質點法，并且在繩網展開階段彈簧質點法也能夠較好的模擬繩網的運動過程[8-9]。對繩網展開階段進行研究并掌握空間繩網的展開規律，可以幫助設計人員確定繩網最佳抓捕時機，對于發射參數的設計也有重大的指導意義。

近年來，國內外學者對空間繩網的展開動力學問題進行了研究，主要集中在繩網展開階段的動力學建模和繩網展開參數的敏感性分析。陳欽等[10-11]較早地使用彈簧質點法建立了空間繩網的動力學模型，并研究了發射角度和阻尼系數對繩網展開過程的影響。張青斌等[12]基于彈簧質點法建立了考慮空氣阻力的繩網動力學模型，并對繩網展開階段的天地差異進行了研究。于洋等[7]分析了發射速率、發射角度和牽引體質量占比對繩網展開性能的影響，并根據數值仿真結果給出了繩網系統的發射參數選擇建議。李京陽等[13]、劉海濤等[14]也進行了類似的研究。國外方面，Salvi等[15]引入質量系數衡量繩網的展開質量，并研究了發射速率、發射角度和繩網構型等對繩網展開質量的影響。Shan等[9]分別使用絕對節點坐標法和彈簧質點法對柔性繩網展開階段的運動過程進行仿真，分析了多種初始條件對繩網展開的影響。Botta等[16]基于能量和動量分析對繩網展開動力學問題進行了研究，同時以最大展開面積、展開時間和有效時間為目標開展了繩網展開階段的敏感性分析。

盡管上述文獻對繩網展開過程中輸入輸出參數的變化規律進行了討論，并根據規律在繩網輸入參數設計方面給出了建議。但是現階段針對提升繩網展開性能方法的探索并不多。高慶玉等[17]借鑒降落傘“先拉出、后展開”思想，提出了一種空間繩網二級發射模式，其研究表明二級發射模式下繩網的最大展開面積以及飛行距離均優于傳統的繩網拋射模式。陳青全等[18]提出一種基于“定力撕裂帶”的網型控制方法，通過在繩網邊線安裝定力撕裂帶來抑制繩網的回彈現象，研究結果表明選取適當的撕裂力能夠提升繩網的展開性能。

本文使用繩網質心和牽引體質心描述繩網展開過程中的回彈現象，將抑制繩網回彈轉變為抑制繩網對牽引體的質心追逐。由此提出通過拖曳繩對展開過程中的繩網施加控制力，降低繩網質心對牽引體質心的追逐，以提高繩網的展開性能。使用彈簧質點法建立了繩網的動力學模型，并基于遺傳算法得到了最優的控制力曲線，通過數值仿真驗證了有控展開相比于無控展開的優勢。

1 空間繩網有控展開原理

1.1 繩網展開的質心追逐現象

繩網的展開過程是指折疊儲存在網包內的繩網在具有一定初速度的牽引體的拖動下，逐漸從網包內抽出并展開的過程。本文將繩網的展開面積定義為4個繩網網角所圍成四邊形的面積，將繩網的展開面積與設計面積的比值定義為展開率。繩網展開率的變化規律是評估繩網抓捕能力和確定繩網抓捕時機的重要因素。繩網的展開過程按照其展開率的變化規律可以分為兩個階段:第一個階段繩網在牽引體的帶動下逐漸展開，繩網網口面積由小變大;展開率到達最大值后進入第二個階段，即回彈階段。繩網被牽引體拉緊，繩網中心由凹變凸，有逐步趕超牽引體的趨勢，四個牽引體逐步收攏，繩網展開率逐漸下降。繩網的回彈造成了網口面積過早減小，降低了繩網的展開性能。所以，可以通過抑制回彈現象提高繩網的展開性能。

為了實現對繩網回彈的抑制，本文首先將空間繩網離散為牽引體及繩網本體，利用兩者的質心變化歷程描述繩網的回彈現象。圖1繪制出了具有正方形網格的四邊形繩網的展開率隨時間的變化歷程及牽引體質心、繩網本體質心的運動歷程，仿真輸入條件同第4節。

圖1 質心追逐過程Fig.1 The chase of the center of masses

可以發現繩網展開率在約2.02 s時達到最大，之后由于回彈現象迅速下降。而0 s時刻由于繩網本體及牽引體位于同一平面，兩者質心位移均為0。隨著繩網的逐漸展開，兩者的質心開始移動，由于牽引體具有較大初速度，其質心位移領先于繩網本體，但是通過圖1可以發現，繩網質心的移動速度要大于牽引體質心。約2.02 s時，繩網質心與牽引體質心到達同一位置，并在后續過程中超過牽引體質心。因此繩網的回彈現象可以描述為繩網質心對牽引體質心的追逐過程，當繩網質心追上牽引體質心時，繩網位于最大展開率附近，此時繩網外形接近平面，無回彈發生。繩網質心的位移超越牽引體的質心時，繩網網面凸出開始回彈。

1.2 基于拖曳繩控制的繩網回彈抑制方法

為了抑制繩網回彈，可以通過降低繩網質心對牽引體質心的追逐速率實現。而完整的繩網系統都具有拖曳繩，用于繩網成功捕獲后將目標脫離至墳墓軌道[19]。同時由于拖曳過程需要保持抓捕目標與拖曳船之間的安全距離，拖曳系統均具有繩系張力控制功能，可以控制拖曳繩對于繩網連接點的拉力。

本研究在不額外增加任何裝置的前提下，通過拖曳系統中的繩系張力控制功能，在繩網展開的過程中對繩網中心的連接點施加持續控制力，從而降低繩網質心的追逐速度，抑制回彈現象，提高繩網的展開性能。有控展開示意圖如圖2所示，發射平臺在繩網完全離開后，通過拖曳繩施加控制力Fcon，在Fcon的作用下繩網本體的速度降低，其質心Mn對牽引體質心Mb的追逐速率也相應降低，最終延緩兩質心的相遇，抑制繩網回彈。由于繩索具有可拉不可壓的特點，Fcon的方向始終朝向發射平臺。控制力方向確定的情況下，如何確定拖曳繩控制力在控制區間內的大小是提高繩網展開性能的關鍵。

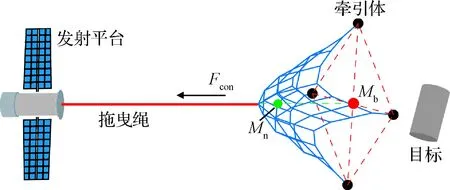
圖2 有控展開示意圖Fig.2 The deployment method with control

2 基于遺傳算法的繩網控制力優化

2.1 繩網性能衡量指標

顯然繩網的展開率越大，成功抓捕目標的概率越高，因此根據展開面積的變化規律，衡量繩網展開性能的衡量指標可以細化為以下5個參數(如圖3所示)：

1)最大展開率：繩網展開的最大面積與繩網設計面積的比值。

2)展開時間：指繩網展開到最大展開率的時間。

3)展開位移：指繩網展開到最大展開率的位移。

4)有效展開時間：繩網展開率超過設定閾值的持續時間。

5)有效展開位移：繩網展開率超過設定閾值的飛行距離，一般采用80%作為閾值[9,13,16]。

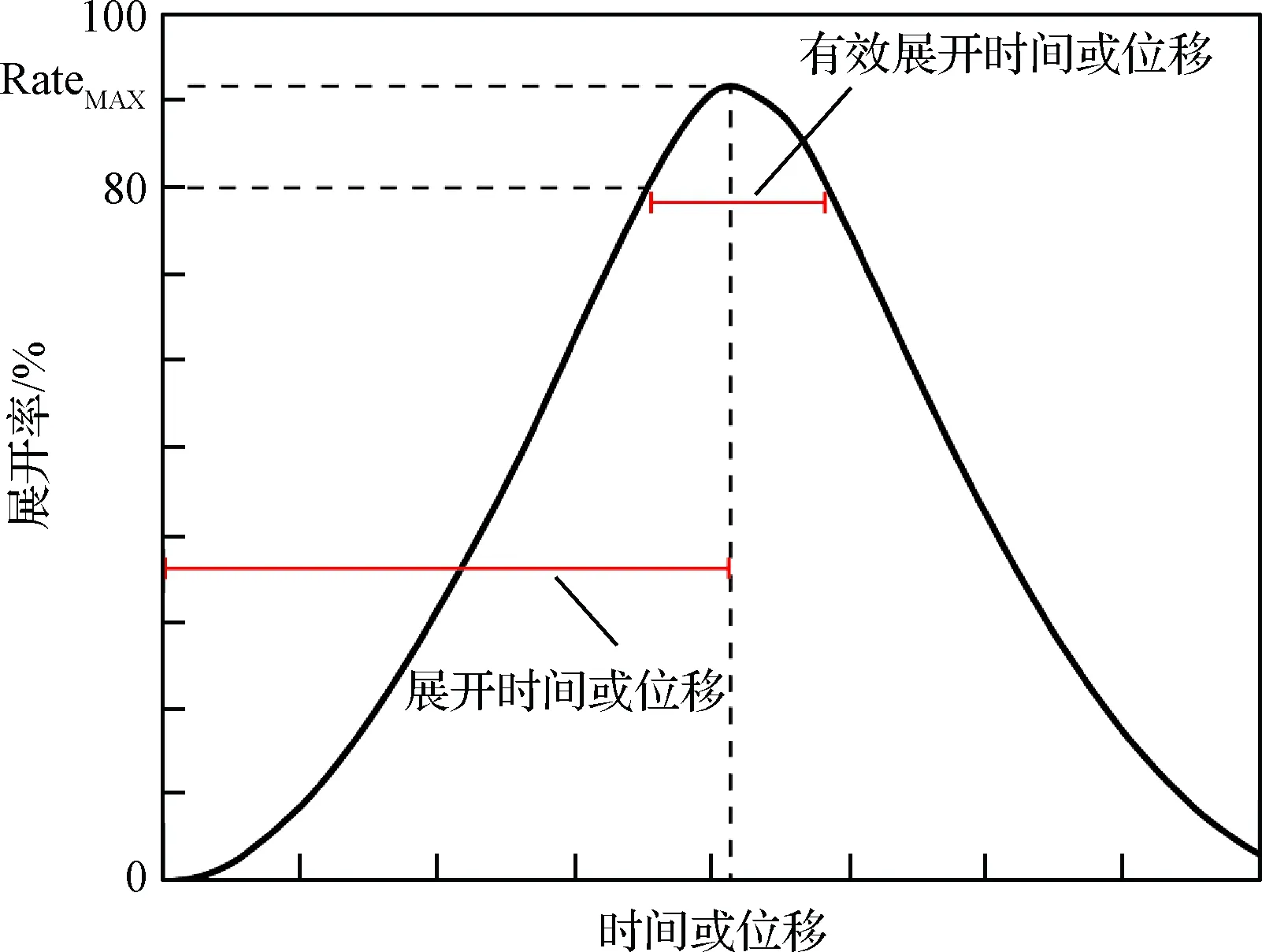
圖3 展開性能指標Fig.3 Performance criteria of deployment

展開時間和展開位移可以為最佳抓捕時機的確定提供依據，這兩個指標可以通過發射速率和發射角度進行調整。盡管展開率越大，抓捕成功的幾率越高，但是通常認為只要展開率超過設定的閾值，抓捕任務便可以完成。并且展開率超過設定閾值后，繩網飛行的距離越遠，其有效抓捕區間覆蓋的距離越大，抓捕目標的成功率越高。因此有效展開位移可以作為衡量繩網抓捕成功率的指標。相比有效展開位移，有效展開時間只能說明繩網展開率超過閾值的時間，對于抓捕成功評估意義不大。同時，由于已經設定了展開率閾值，繩網最大展開率的大小在本文中不做重點討論。

綜上所述，較大的有效展開位移表示繩網抓捕區間覆蓋范圍較大，能夠提高抓捕成功率。所以選擇有效展開位移de作為本研究的優化目標，并使用80%作為本研究的閾值。

2.2 控制力曲線優化

空間繩網的展開是一個非線性的動力學過程，拖曳繩對繩網的控制力需要隨時間而變化才可能使得繩網展開性能得到提高。因此可以將繩網性能優化問題細化為繩網最優控制力曲線優化問題。如果將每一時刻的控制力大小作為優化對象，顯然可以得到最佳的有效展開位移優化結果。但是相鄰時刻的控制力大小波動較大，將影響控制系統對于控制力曲線的跟蹤精度，增加張力控制系統的負擔。

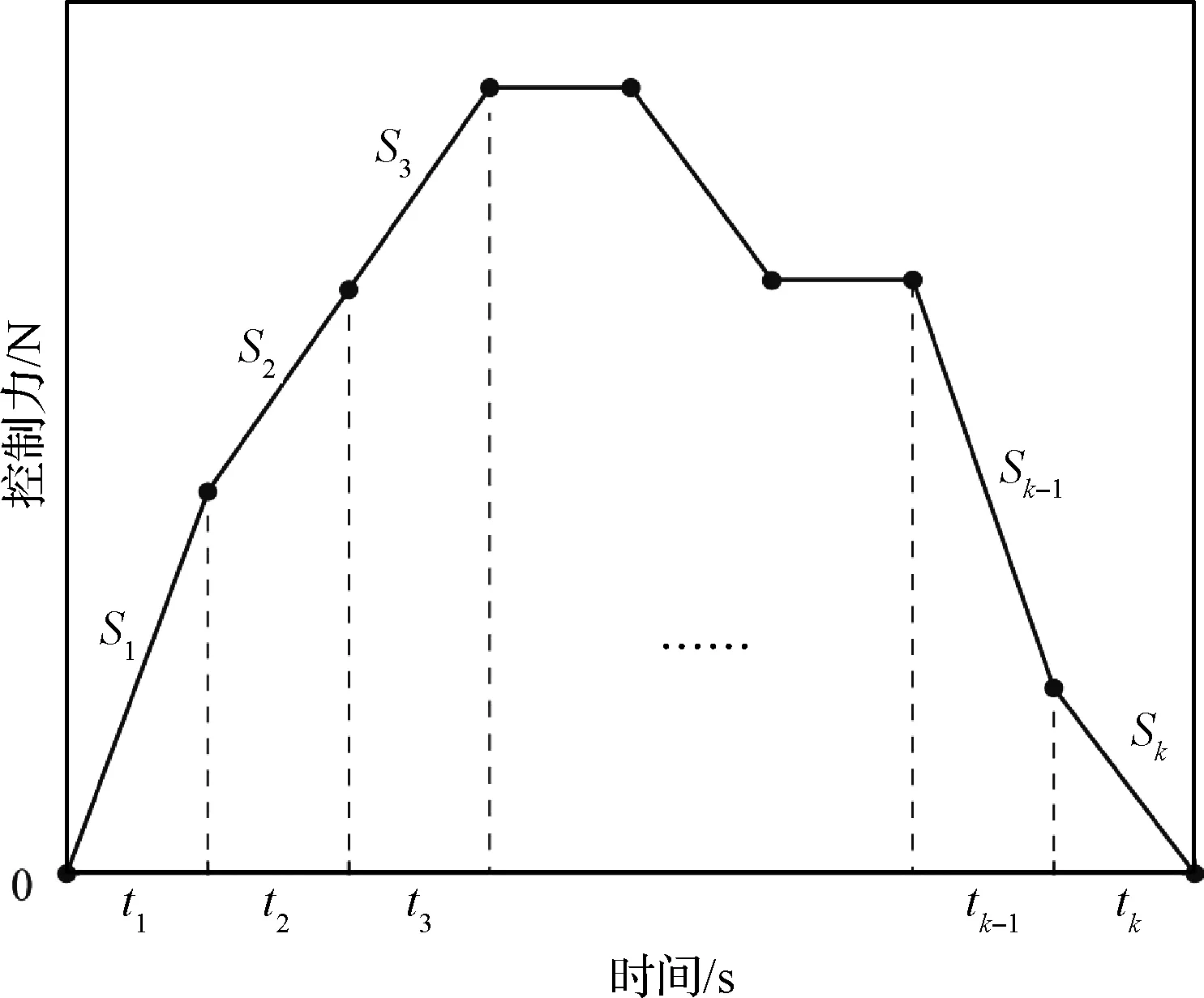
圖4 控制狀態序列示意圖Fig.4 The sequence of control state

遺傳算法是一種模擬生物進化機制的全局優化算法，不需考慮所優化問題的內在工作原理，可以處理定義在離散、連續或混合搜索空間上的線性或非線性目標函數[20-21]。本研究設置3個增大檔位和3個減小檔位，即|p|=|q|=3，并使用整數編碼對包含保持檔在內的7個檔位進行編碼。各個檔位對應的控制力變化率和編碼值如表1所示。

表1 控制力變化率檔位編碼Table 1 Code of control gear

通過優化控制力曲線，使得繩網的有效展開位移de最大化。控制力的初始值應為0，考慮到在實際工況中繩網與目標的碰撞接觸發生在結束施加控制力之前，因此不對控制結束時刻的控制力進行約束，在控制結束后將控制力歸零。由于繩索“可拉不可壓”的特性，拖曳繩只能對繩網施加朝向平臺的拉力。若將朝向平臺的拉力方向設定為正，則整個控制階段繩網的所受拉力均為非負值。綜上，繩網的控制力曲線優化問題可以描述為：

(1)

其中，tst為控制區間的開始時間，tend為結束時間。

在已知控制狀態序列時，可以反推出任意時刻控制力的大小。若t時刻時處于第i個控制狀態區間，則此時刻的控制力可以表示為：

(2)

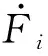
3 繩網動力學模型

使用彈簧質點模型對繩網進行建模的基本原理是將繩網離散為有質量的質點和質點間無質量的彈簧、阻尼器單元。計算各質點的受力并建立相應的動力學方程，最后通過聯立各個質點的動力學方程得到繩網的位移及受力情況。

本研究對網格為正方形的四邊形繩網進行研究，繩網網角依次連接四個牽引體。將繩網物理節點視為集中質量，繩段視為彈簧和阻尼器并聯的無質量單元，繩網的構型及離散方法如圖1所示。

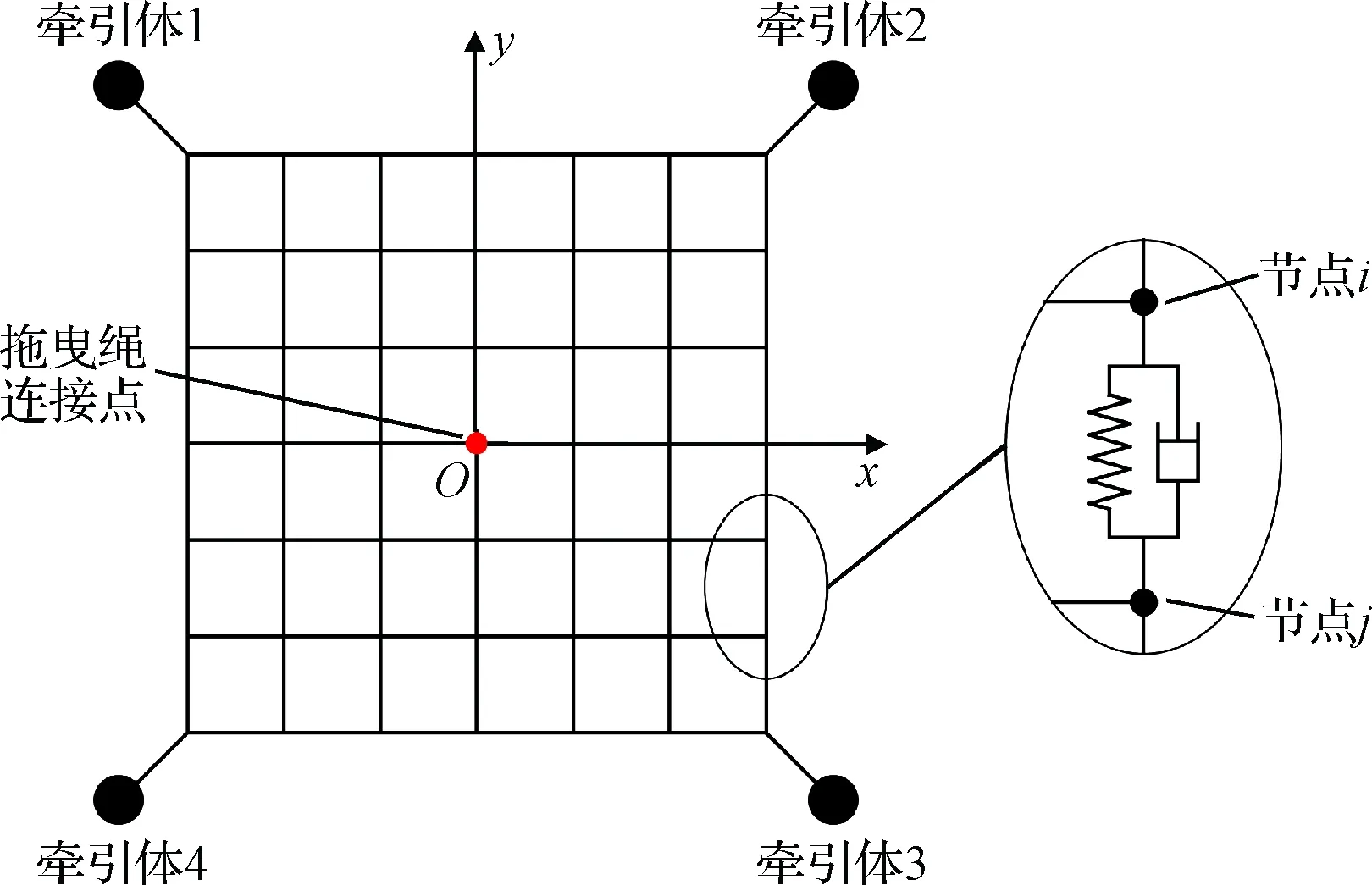
圖5 繩網構型Fig.5 Configuration of the tether-net

根據牛頓第二定律，質點i的動力學方程為：

(3)

其中,mi為質點i的等效質量，根據質點在繩網內的位置分布有如下定義：

(4)

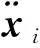
Fext,i=Fcon·eL

(5)

其中,eL是指向發射平臺的單位向量。Fint,i是相鄰繩段傳遞給質點的內力，表示如下：

(6)

當繩段端點距離大于繩段原始長度時，繩段中產生拉力，當繩段端點距離小于繩段原始長度時繩段內不產生拉力。因此在以i,j為端點的繩段中，i點所受張力如下式：

(7)

式中:kij是網繩的等效剛度系數：

kij=EA/l0

(8)

式中:E是繩網選用材料的楊氏模量，A是網繩的橫截面積，lij是繩段的真實長度，l0是繩段的原始長度。eij是從i指向j的單位向量，vij是質點i與質點j的相對速度。dij是阻尼系數：

(9)

式中:ζ為繩網選用材料的阻尼比。

4 仿真結果及討論

4.1 恒定控制力

首先通過數值仿真研究繩網控制力Fcon為恒力的情況。建立三維笛卡爾坐標系，將繩網收納放置在坐標系原點處，繩網的飛行方向為z軸正向。牽引體的發射速率vb=7 m·s-1，發射角度θb=30°，其中θb是牽引體的發射方向與繩網飛行方向(z軸)的夾角。同時本文算例在理想空間環境中進行，不考慮引力、攝動及空氣阻力，所研究繩網的參數如表2所示。

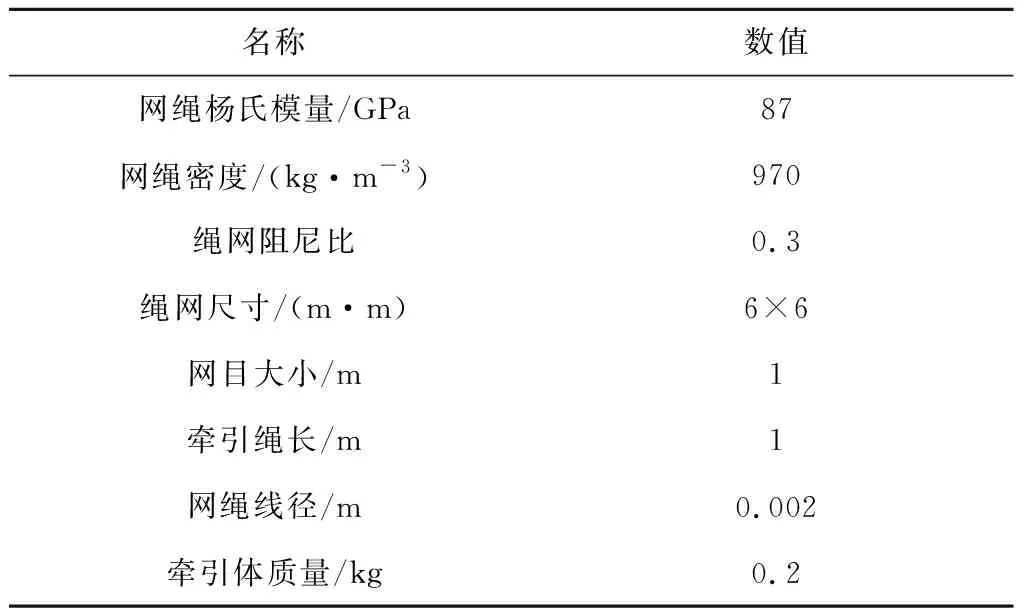
表2 繩網參數Table 2 Simulation parameters

基于上述輸入參數，無控制力時繩網在約1.08 s時能夠完全離開發射平臺，在約2.47 s時展開率能夠第二次達到80%的閾值，如圖8所示。為了統一展開性能的衡量標準，本研究中的控制力施加時間均設置為1.1～2.5 s。同時，本研究使用Matlab編寫繩網仿真程序，所有算例的仿真時長均設置4 s。設置一系列恒定控制力水平如表3所示。并對不同控制力下的繩網展開過程進行仿真。

表3 恒定控制力列表Table 3 List of constant forces

圖6給出了控制力為恒力時繩網面展開率隨位移的變化曲線。表4給出了相比無控工況，不同控制力下繩網有效展開位移的提升率。可以發現，當控制力為恒力時，隨著控制的增大，繩網的有效位移得到少量提升。當控制力為0.5 N時有效位移的提升率最高，為9.52%。若控制力繼續增加，則提升效果顯著下降。當控制力大于2 N時，繩網的整個展開階段均無法到達80%的設定閾值。值得注意的是，控制力的施加會降低繩網系統的總動能，因此施加控制力后繩網的最大展開率低于無控工況。綜上可知，僅僅通過拖曳繩對繩網施加恒定的控制力對繩網有效展開位移的提升有限，因此有必要通過調節控制區間內每一時刻的控制力大小使得繩網的展開性能進一步提升。

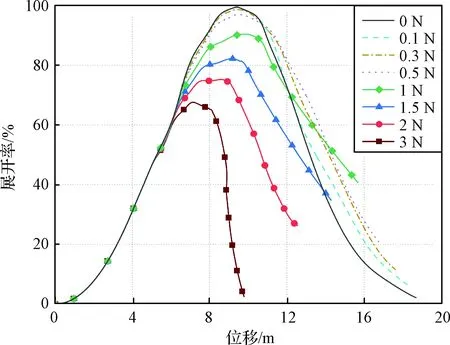
圖6 展開率隨位移變化曲線Fig.6 Comparison of deployment simulation results with constant force

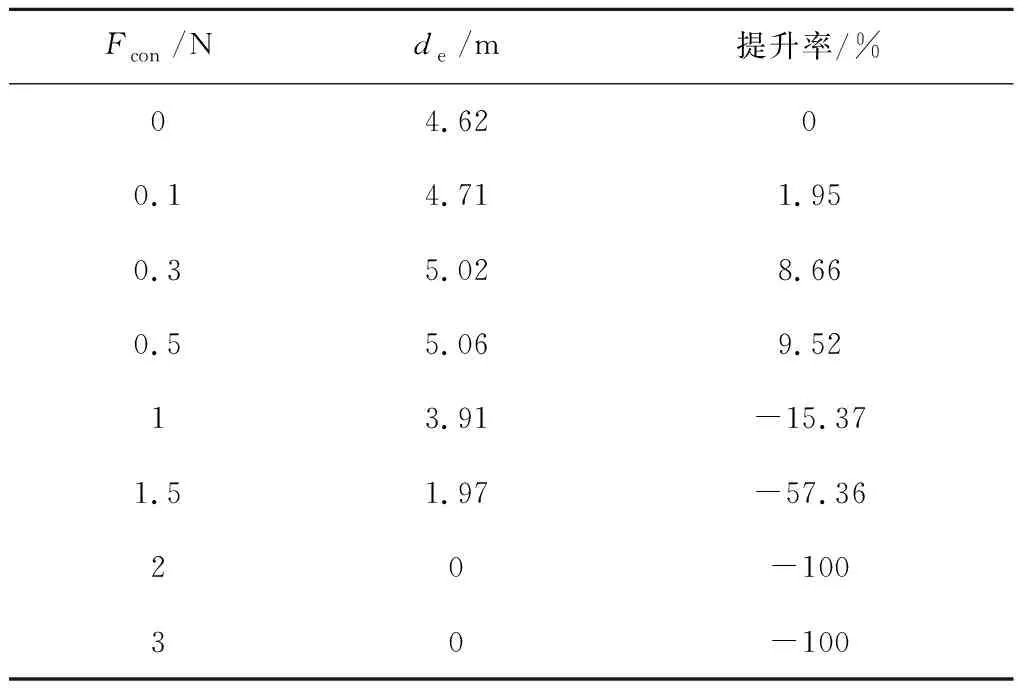
表4 有效展開位移提升率Table 4 The increase of the effective displacement

4.2 變控制力

為了進一步提升有控狀態下繩網的展開性能，使用經過遺傳算法優化的控制力曲線進行研究。本節使用的繩網參數和發射參數與4.1節相同。使用Matlab編寫了采用整數編碼的遺傳算法，初始種群規模為40，進化代數為100。控制區間為1.1～2.5 s，并將此區間離散為10段，控制力檔位及編碼值如表1所示。優化后的控制力檔位序列及對應的控制力變化率見表5。

表5 優化后的檔位序列Table 5 Optimized sequence of control gear

優化后的控制力曲線及對應檔位如圖7所示。可以發現，優化后的控制力呈現“增-減-增”的變化趨勢。最大控制力出現在1.38～1.52 s處，大小為1.68 N。最小控制力出現在2.22 s處，大小為0 N。

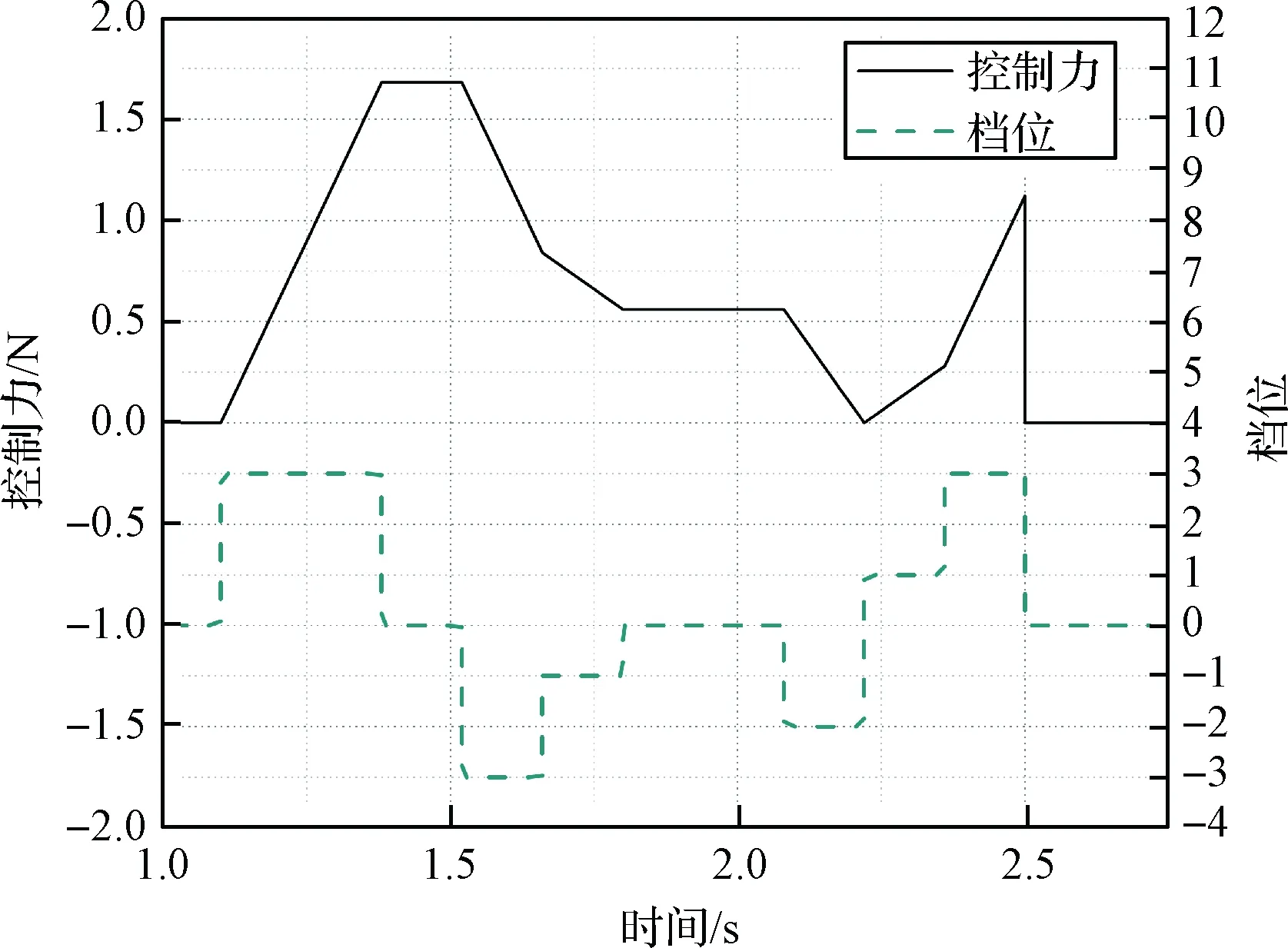
圖7 優化后的控制力曲線及檔位Fig.7 Optimized control force and control gear

繩網的展開率隨時間、位移的變化曲線分別如圖8和圖9所示。無控繩網的展開率在1.54 s時首次達到80%，此時對應的飛行位移為6.93 m。在2.47 s時無控繩網的展開率第二次達到80%，之后迅速下降，此時對應的飛行位移為11.55 m，無控繩網的有效展開位移為4.62 m。有控繩網的展開率分別在1.68 s和3.35 s處到80%，對應的飛行位移分別為7.55 m和14.21 m。可知有控繩網的有效展開位移為6.66 m，相比無控繩網提升了約44.16%。由于控制力的作用，有控繩網的動能相比無控繩網有所下降，其最大展開率低于無控繩網。

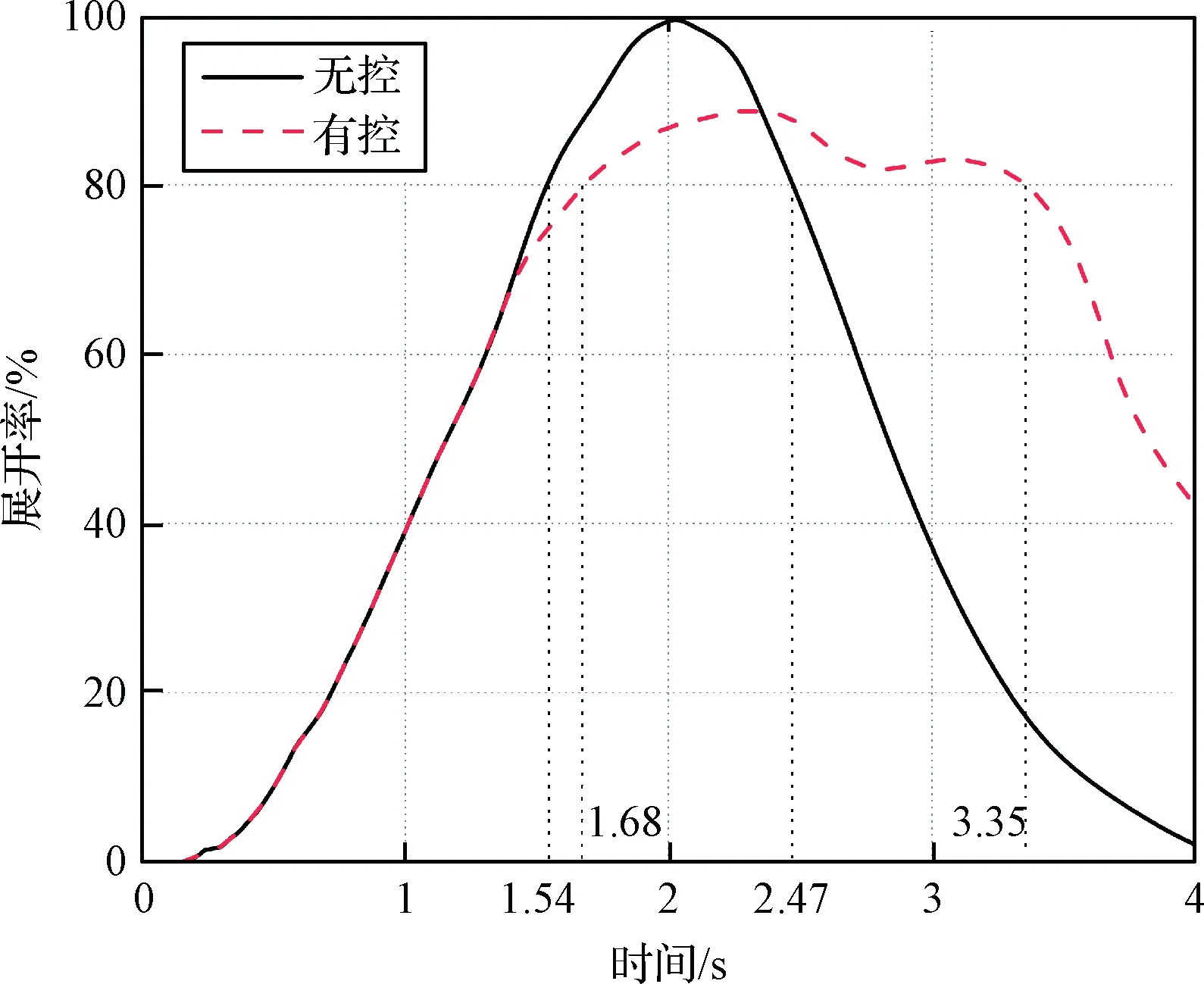
圖8 展開率的時間歷程Fig.8 Time history of deployment rate with and without control

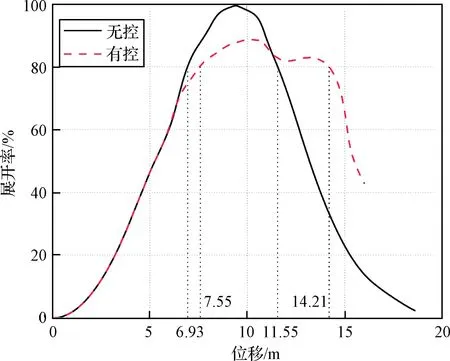
圖9 展開率隨位移變化Fig.9 Displacement history of deployment rate with and without control

圖10中，進一步繪制了無控繩網展開率第一次、第二次達到80%時，以及有控繩網展開率第二次達到80%時，無控、有控下繩網的網形圖。1.54 s時無控繩網的展開率首次達到80%，此時無控、有控兩種工況下繩網的形態及展開率均較為接近。由于控制力的作用，有控繩網的底部呈現凸起。2.47 s時無控繩網的展開率第二次達到80%，此時有控繩網的展開率高于無控繩網，約為87%。此時無控繩網的網體已經在z軸正向超越了牽引體，并出現了明顯的回彈現象。而有控繩網上表面的網形較為平整，由于控制力的作用繩網中心在z軸負向出現了較為明顯的下凹。3.35 s時有控繩網展開率第二次達到80%，此時有控繩網出現了回彈現象，但是其展開率依舊滿足抓捕需求。而此時無控繩網的展開率已經不足20%，其網體部分也出現了穿透和纏繞現象，無法進行有效抓捕。通過上述分析可知，展開過程中，有控繩網在網形保持、有效展開位移等性能指標上均優于無控繩網。

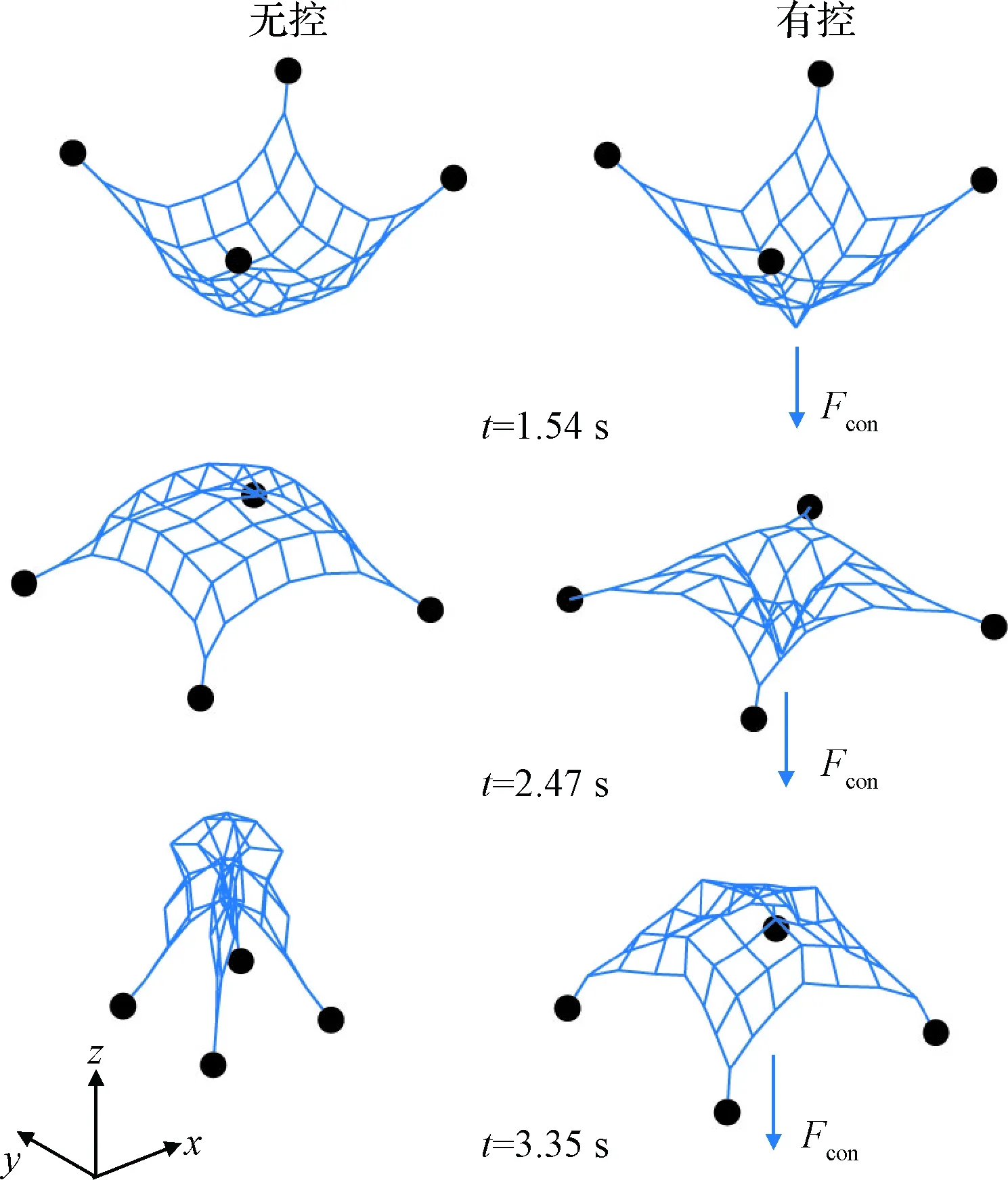
圖10 網形對比Fig.10 Deployment sequence with and without control

分別繪制了繩網和牽引體的質心位移隨時間的變化曲線，如圖11所示。可以發現，無論是否施加控制力，繩網質心對牽引體質心都存在追逐趨勢，并最終超越牽引體質心。無控工況中，兩質心在約2.02 s時相遇，此時的位移為9.33 m。施加控制力后，兩質心在約2.2 s處相遇，位移為9.62 m。控制力推遲了質點的相遇時間，使得質心交點延遲出現了0.18 s，并使得相交時的位移延長了0.29 m。

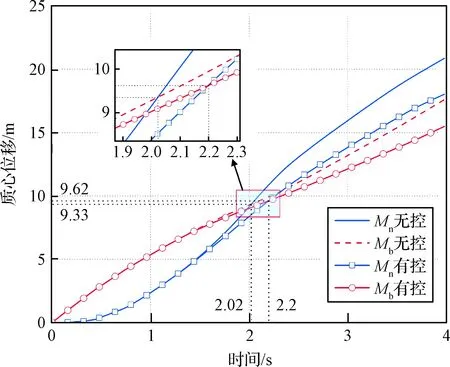
圖11 質心位移對比Fig.11 Displacement of the centers of masses

圖12分別給出了繩網和牽引體的質心追逐速率。無控工況中，由于需要牽拉繩網，牽引體質心的速率首先呈現下降趨勢，而繩網質心的速率逐漸上升。在約2 s時繩網質心達到最大速率約為0.178 m·s-1，牽引體質心達到最小速率約為0.065 m·s-1。此時繩網的展開率接近最大值，并開始出現回彈現象。之后繩網質心的速率逐漸下降，而牽引體質心的速率逐漸上升。這也說明了使用質心追逐描述繩網回彈現象的正確性。有控工況中質心速率的變化趨勢與無控工況類似。但是，開始施加控制力后，相比無控工況，有控工況下兩質心的速率均出現了顯著下降。并且在控制區間內，繩網質心速率的下降幅度要大于牽引體質心速率的下降幅度。這說明控制力成功推遲了兩質心相遇的時間，抑制了回彈現象，最終提高了繩網的展開性能。

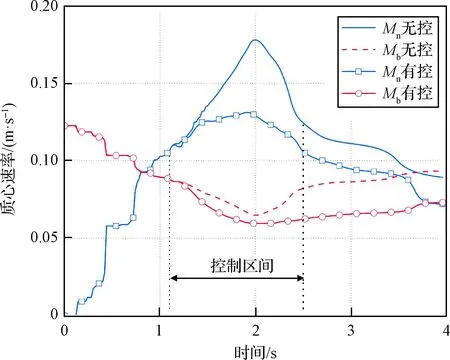
圖12 質心追逐速率Fig.12 Velocity of the center of masses

5 結 論

針對繩網的回彈現象提出了一種基于拖曳繩張力控制的繩網展開控制方法。使用繩網和牽引體的質心描述繩網展開過程中的回彈現象，將抑制繩網回彈轉化為抑制繩網對牽引體的質心追逐。由此提出通過拖曳繩對展開過程中的繩網施加控制力，降低繩網質心對牽引體質心的追逐速率，以提高繩網的展開性能。以控制力變化率為優化對象，以繩網有效展開位移為優化目標，提出了一種基于遺傳算法的控制力曲線優化策略。基于彈簧質點法建立了繩網的動力學模型，并通過數值仿真對比了無控、恒力和變力控制下繩網的展開性能。通過研究得出以下結論：

1)提出的質心追逐可以較好地描述繩網的回彈現象，為后續繩網高性能展開方法的提出提供思路。

2)僅施加恒定控制力難以有效提高繩網的展開性能，提出的控制力優化策略可以成功優化出所需控制力曲線。

3)提出的有控展開方法可以有效抑制繩網的回彈現象，相比無控工況可以將繩網有效展開位移提高約44.16%，但最大展開率會有所下降。