運載器式潛射導彈水面分離運動特性

陸辰昱，王 鑫，周志壇，梁曉揚，樂貴高

(1. 南京理工大學機械工程學院，南京 210094；2. 中國人民解放軍96901部隊，24分隊，北京 100094)

0 引 言

潛射導彈的發射方式目前主要有兩種：濕式發射和干式發射。采用干式發射時，運載器包裹著導彈在水下航行。期間導彈不與水直接接觸，并且大部分水動力載荷由運載器承擔。當運載器穿過水面時，導彈助推器點火推動其與運載器分離，轉入空中飛行彈道[1]。彈器分離階段雖然時間短，卻提供了導彈空中飛行的初始條件，是發射成功的關鍵[2-3]。然而分離過程在自由液面進行，受海浪和多體相互作用等因素影響，分離運動呈現很強的非線性。因此，有必要對運載器式潛射導彈水面分離運動特性加以研究。

目前國外關于多體出水分離運動的研究較少，關注更多的是單體跨介質運動[4-5]和空中多體分離問題[6-8]。而國內則有較多學者開展了飛行器出水分離的相關研究。彭正梁等[9]建立了高速航行體與運載器水面分離的線性多體動力學方程，并基于勢流理論計算了水動力，進而對該過程進行了二維彈道仿真；顧媛媛等[10]基于切片法建立了航行器水面分離的動力學模型，并通過Matlab進行數值模擬，研究了分離過程中航行器的運動參數變化；李晶等[11]對筒式導彈出水分離過程進行了研究。通過受力分析建立了多體動力學方程，進而計算了分離過程中姿態和速度等參數的變化；劉曜等[12]通過構建動力學方程組對潛射導彈的水下彈道和水面分離彈道進行了仿真研究，并通過與水洞試驗對比驗證了計算模型的精確性。以上研究為運載器式潛射導彈水面分離過程的預測提供了一定的參考依據。然而，目前絕大多數研究缺乏對液體相的模擬，且在處理水動力問題時均采取如勢流理論等簡化的液體流動模型。實際情況下，運載器出水分離伴隨著海浪的擾動以及波浪的破碎，其受力情況較為復雜。因此，需要在計算運載器與導彈分離運動的同時，精確地模擬自由液面的狀態。

本文建立了自由液面模型和六自由度運動方程，并將以上多介質耦合模型的計算結果與實驗數據對比。在驗證了計算模型的精度和有效性基礎上，對不同海況以及出水角度下運載器式潛射導彈水面分離過程中的質心位移，姿態角及軸向速度等進行了三維仿真計算。本文的數值方法和仿真結果可以為水面分離系統的設計提供指導。

1 分離過程與坐標系建立

如圖1所示，運載器在水下發射出筒后依靠慣性和浮力上升，隨后沖出水面。此時運載器蓋中傳感器獲得信號，繼續上升一段距離后運載器頂蓋拋落，隨后導彈助推器點火產生推力，推動導彈向上運動。同時，運載器受反推力作用落入水中，完成運載器式潛射導彈的水面分離[13]。在此過程中如圖2建立固定坐標系o0x0y0z0，運載器移動坐標系o1x1y1z1，導彈移動坐標系o2x2y2z2。初始時刻(t=0 s)移動坐標系與固定坐標系保持平行。其中o0位于初始時刻運載器頂端中心，o1位于運載器質心，o2位于導彈質心。o1z1與o2z2分別沿著運載器與導彈軸線方向。記運載器動坐標系及導彈動坐標系與固定坐標系之間的歐拉角為滾轉角φ，俯仰角θ，偏航角ψ。

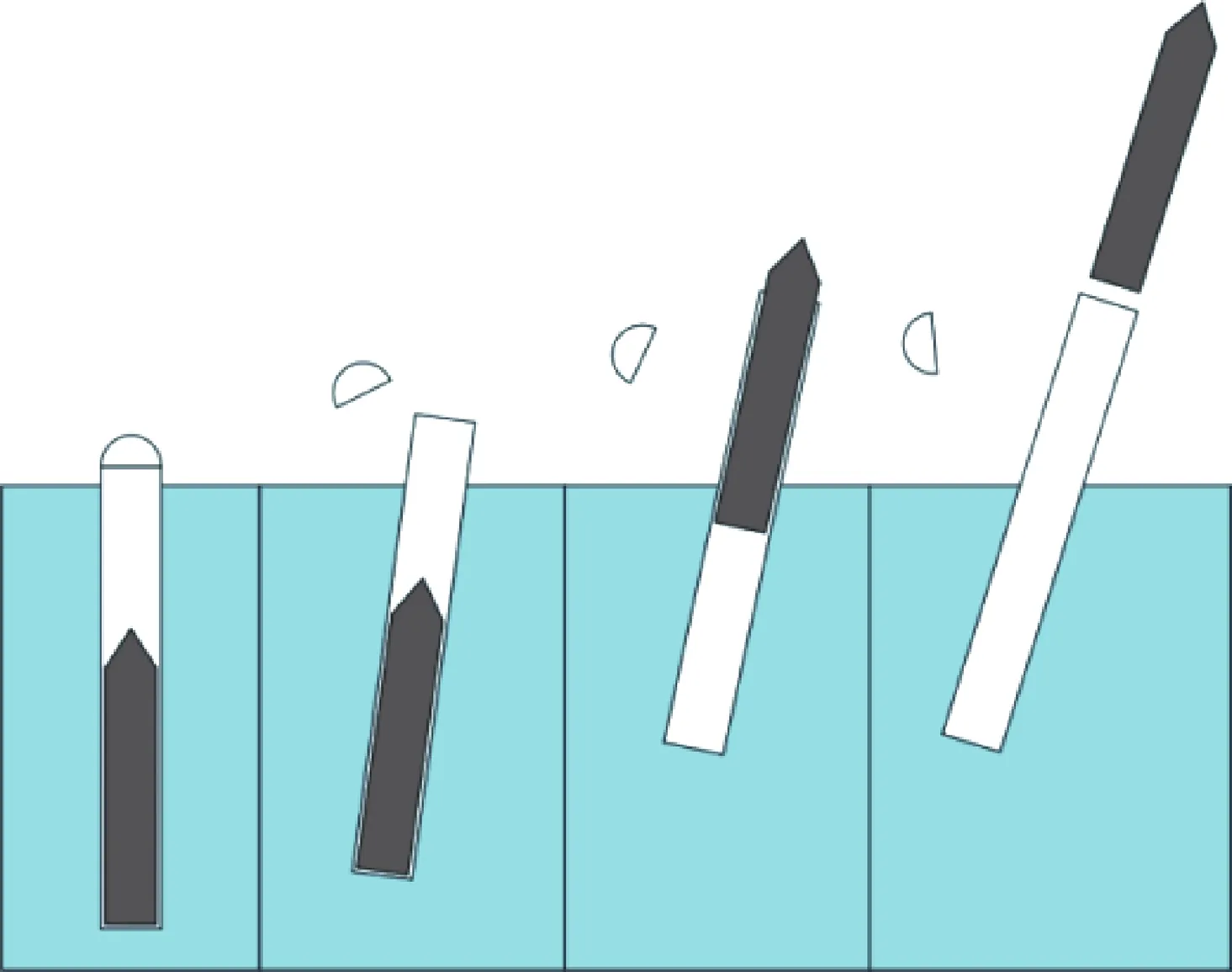
圖1 運載器式潛射導彈水面分離過程示意圖Fig.1 Schematic diagram of separation process of sub-marine launched missile near the free surface

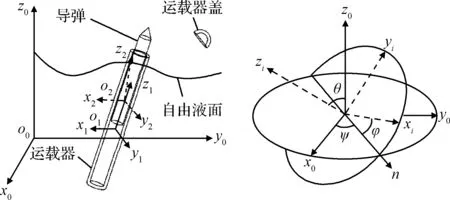
圖2 坐標系示意圖Fig.2 Schematic diagram of coordinate systems

2 計算模型

如圖3所示，運載器式潛射導彈采用單筒單彈結構。運載器直徑為1 m，長度為10 m，材料密度為500 kg/m3；導彈直徑為0.6 m，長度為6 m，材料密度為1000 kg/m3；運載器初始出水速度為10 m/s；導彈在運載器出水后0.5 s開始點火產生推力，推力大小為100 kN，同時，運載器受到同樣大小的反向推力。為了適應運載器與導彈的姿態分布并充分模擬波浪的傳遞過程，需要較大的計算域。

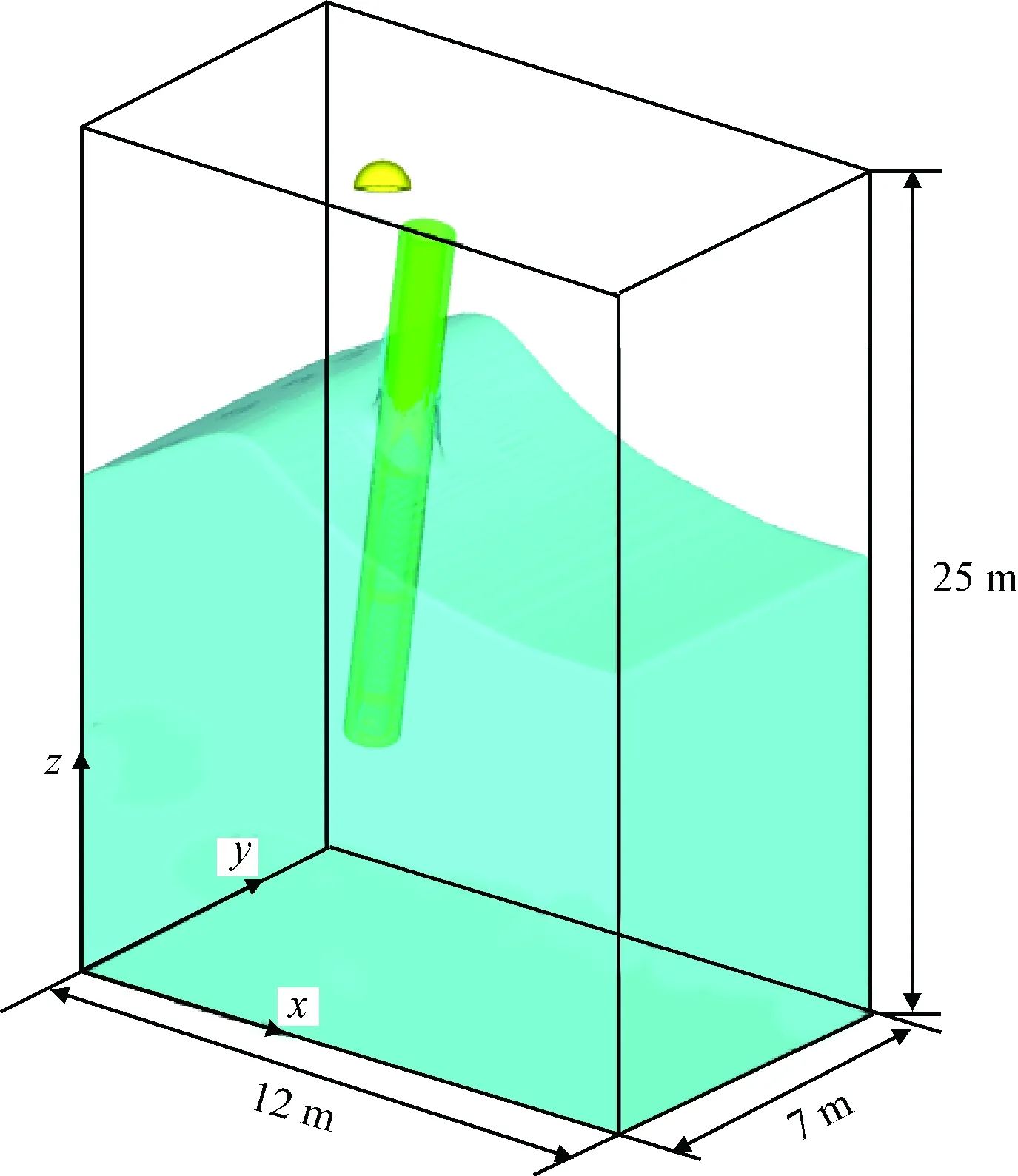
圖3 水面分離計算模型Fig.3 Computational model of separation near the free surface

本文為了研究海面波浪以及出水角度對運載器式潛射導彈水面分離運動特性的影響，共設立三組計算工況如表1所示。其中工況2與工況3均采用5級海況下的浪高。

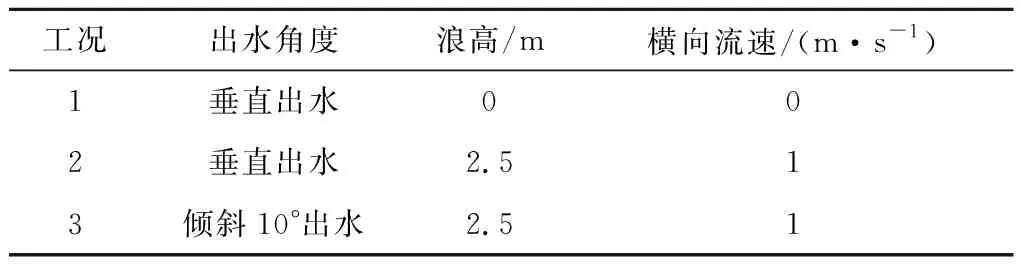
表1 計算工況Table 1 Computational conditions

3 數值方法

3.1 自由液面模型

基于分數容積障礙法(FAVOUR)[14]，建立笛卡爾坐標系下的三維不可壓縮Navier-Stokes方程，形式如下：

(1)

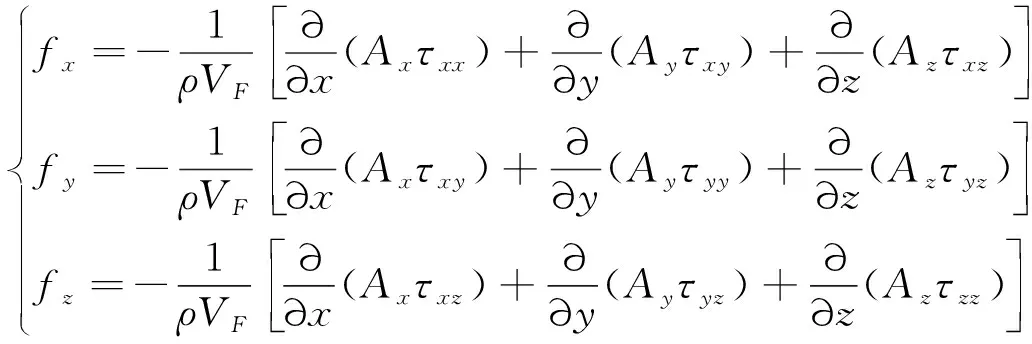
(2)

(3)

式中：ρ為流體密度；u，v，w分別為流體速度在x，y，z方向上的分量；Ax，Ay，Az分別為流體在x，y，z方向上的面積分數；VF為流體的體積分數；p為流體壓強；Gx，Gy，Gz為重力加速度；fx，fy，fz為黏滯力加速度。

湍流模型采用RNGk-ε湍流模型[15-16]，與標準k-ε模型相比，它更適于描述有強剪切區域的流動，因此可以更精確地計算水面波浪破碎過程。其中湍動能k方程為：

(4)

式中：ui，uj為xi，xj方向上的速度分量；μ為流體黏度；μt為動力黏度；Gk為平均速度梯度引起的湍動能k的產生項；常數系數σk=1.39。

湍動耗散率ε方程為：

(5)

(6)

對自由液面采用由Hirt等[17]提出的流體體積函數(VOF)進行求解。通過計算網格單元中流體和網格體積比函數F(x,y,z,t)來確定自由液面邊界。函數F滿足如下控制方程：

(7)

3.2 六自由度運動方程

假設運載器和導彈均為剛體，則其一般運動可分為平移與轉動。因此，分離運動方程形式如下：

(8)

式中：F為剛體所受的總外力，m為剛體質量，V為質心速度，T為作用在質心的總力矩，ω為剛體角速度矢量，J為剛體動坐標系下的慣性張量。

若定義B為運動剛體表面上的任意一點，則該點速度可由下式計算：

VB=V+ω×rB

(9)

式中：rB為質心到B點的矢量。

基于FAVOR法和流體連續性方程，剛體運動的控制方程如下[18]：

(10)

式中：Vc為網格單元的體積；SB，n，VB分別為網格單元內運動物體的表面積、單位法向量和速度。

對于剛體之間的碰撞運動采用Stronge[19]提出的多體動力學方程進行求解。假設碰撞過程無摩擦，兩碰撞體的質量為M和M′，其質心分別位于點G和G′，碰撞接觸點分別為C和C′。在接觸點建立碰撞參考系n1n2n3。其中,n1和n2位于公共切面，n3沿著公共切面的法線方向。根據愛因斯坦求和公式，接觸點C和C′之間的相對速度vi可由下式計算：

(11)

3.3 數值模型關系與計算精度

通過上述模型可在每一個時間步內完成流體與剛體的計算。各模型之間的數值傳遞關系如圖4所示。數值模擬過程采用有限差分法對控制方程進行離散處理，并在時間和空間上保持一階計算精度。

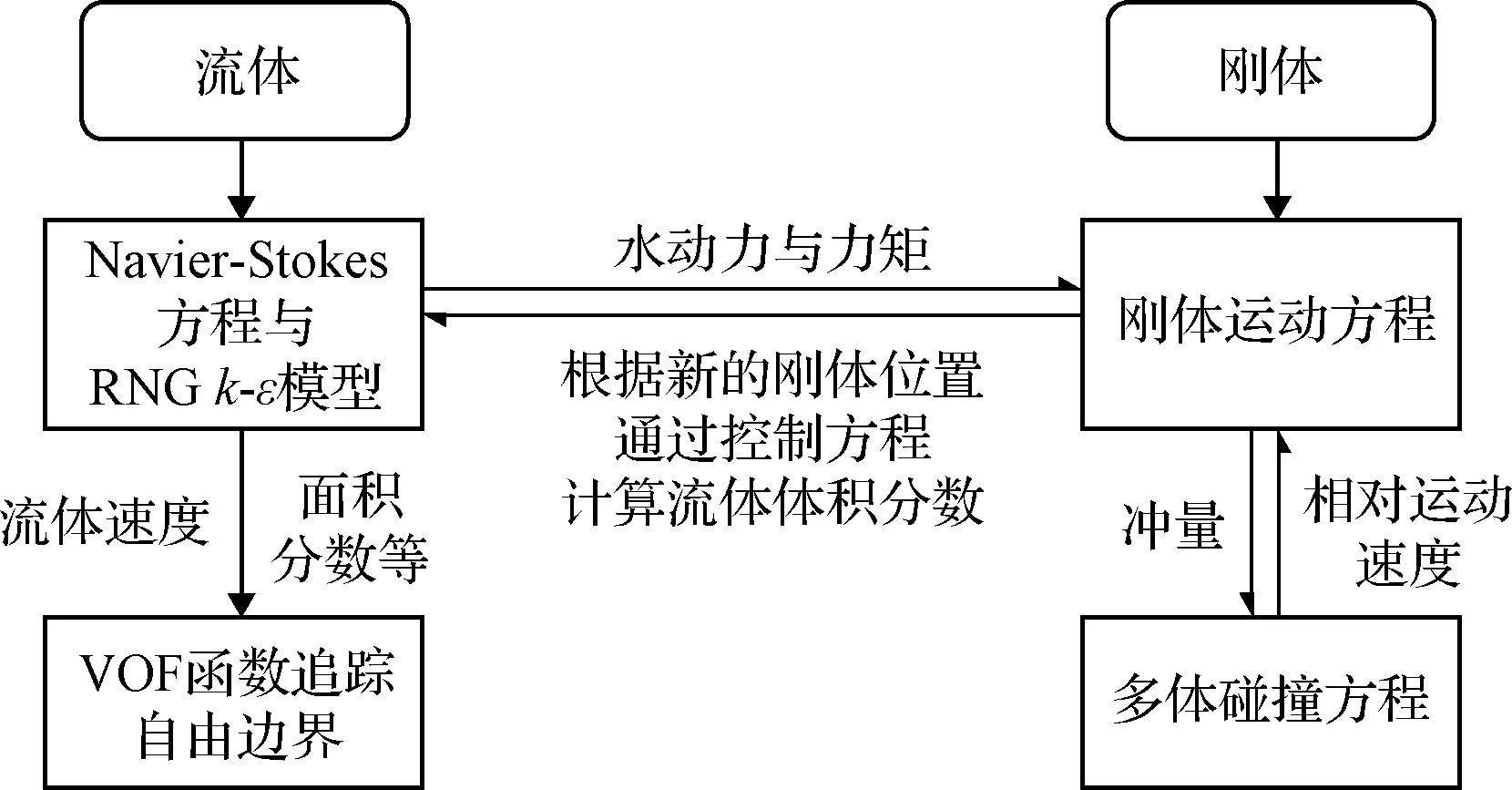
圖4 數值模型關系Fig.4 Relationship between numerical models

3.4 模型驗證

根據上述自由液面模型與六自由度運動方程，如表2所示，對不同初始傾斜角度的圓柱入水過程進行計算，并與實驗結果[20]對比以驗證模型的精確性。圓柱的長徑比為4，密度為900 kg/m3。圓柱初始入水速度垂直向下。受實驗誤差影響，其數值略有波動。

圖5顯示了初始傾角為55.6°，5個不同時刻下，計算結果的速度云圖與實驗高速攝影圖的對比情況。從圖5可以看出,兩者各時刻圓柱的傾角基本一致，且圓柱兩端由于高速入水產生的空泡外形也較為相似。圖6顯示了初始傾角為55.6°，圓柱入水過程中質心位置和質心垂直速度的計算值與實驗測量值的變化曲線。從圖6可以看出，計算結果的質心位置與實驗結果較為吻合。同時，兩者的質心垂直速度也基本一致，僅在末端出現輕微誤差。這主要是受計算網格限制，無法完全模擬空泡拉斷過程中的細小氣泡而造成。

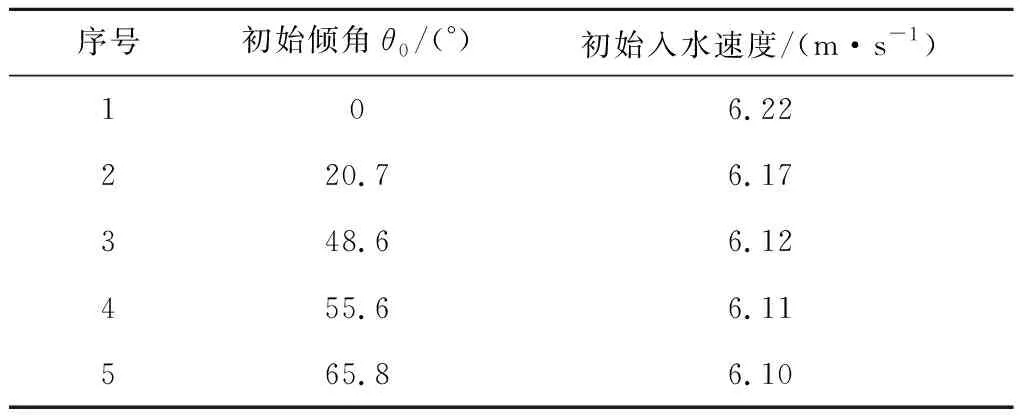
表2 圓柱入水初始條件Table 2 Water entry conditions of the cylinder

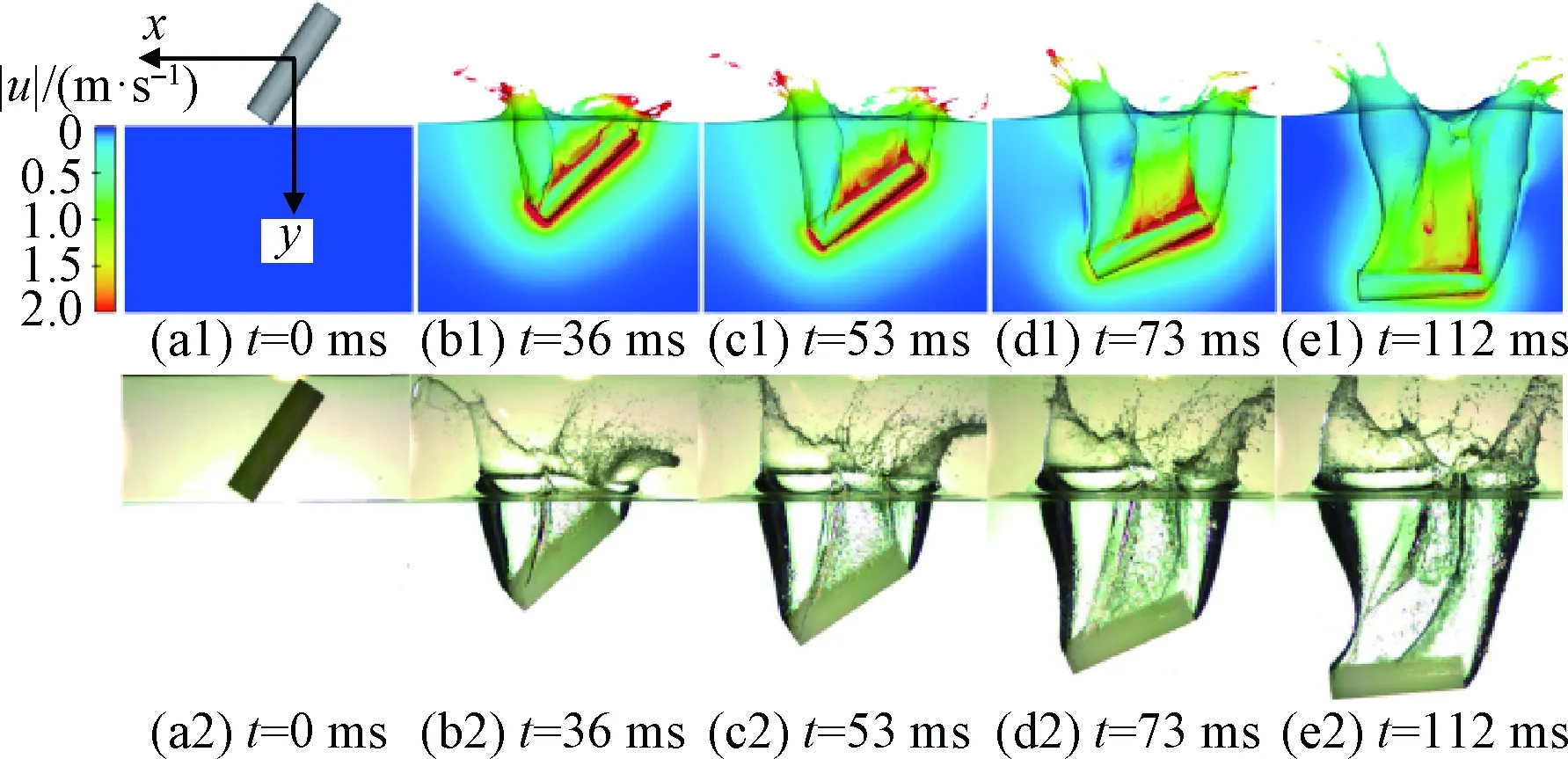
圖5 速度場計算結果與實驗高速攝影圖像(θ0=55.6°)Fig.5 Calculated results of velocity magnitude and high-speed photographs(θ0=55.6°)

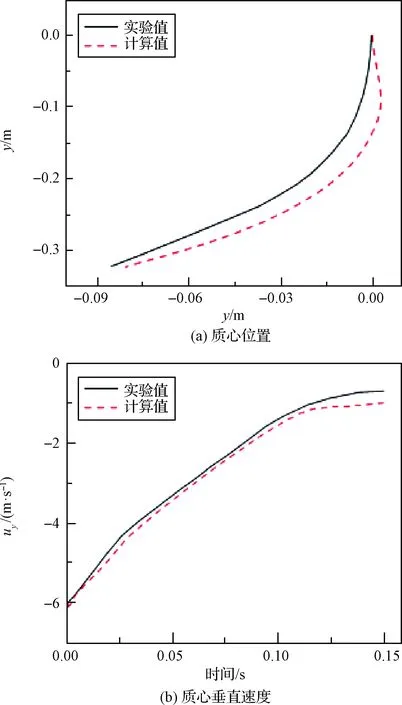
圖6 質心位置與質心垂直速度對比(θ0=55.6°)Fig.6 Comparison of mass center position and comparison of mass center vertical velocity(θ0=55.6°)

在此基礎上，對其余初始傾角的工況也進行了對比計算。如圖7所示，不同初始傾角下圓柱入水，在100 ms時兩端的空泡形狀仍較為相似。同時，從圖8可以看出，計算得到的圓柱入水角位移曲線與實驗值保持較好的吻合。綜上，仿真模型具有較高的精度。

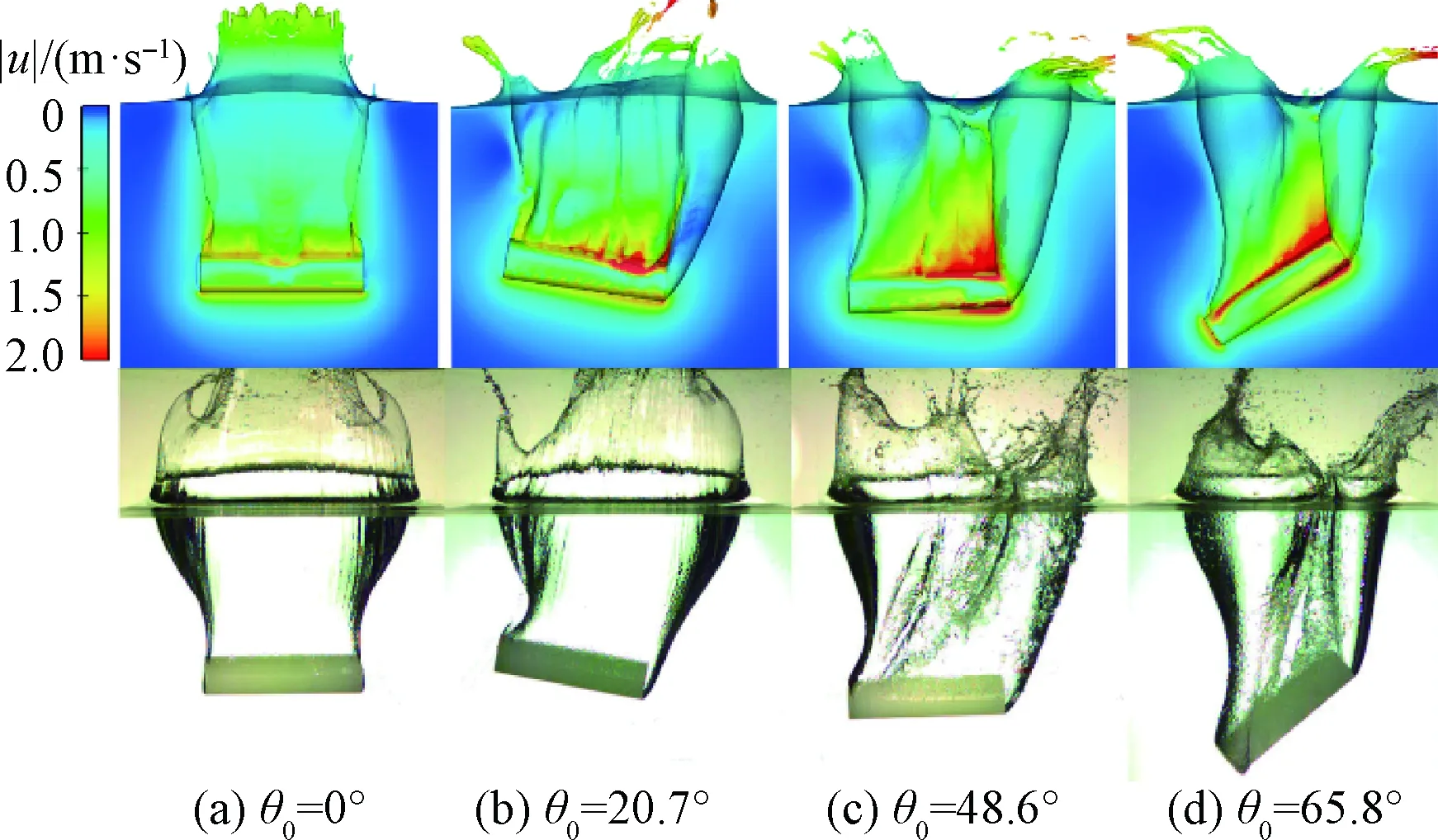
圖7 速度場計算結果與實驗高速攝影圖像(t=100 ms)Fig.7 Calculated results of velocity magnitude and high-speed photographs (t=100 ms)

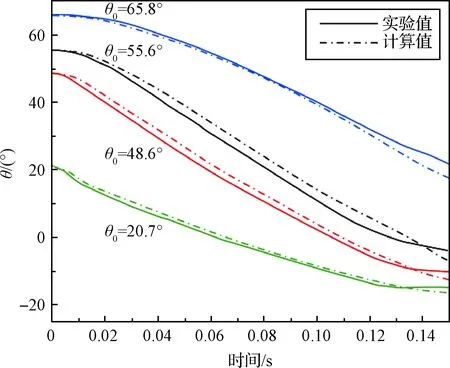
圖8 不同初始傾角下圓柱入水角位移對比Fig.8 Comparison of angular displacement for the water entry with different initial inclined angles

4 計算結果及分析

4.1 分離狀態

圖9為各工況下y+方向的分離狀態圖像序列。由圖9可知，從t=0.5 s導彈產生推力開始，工況1～3均在1.03 s完成分離過程。其中，工況1由于海面無波浪且海水橫向流速為0 m/s，運載器與導彈在分離后仍能保持相對垂直的姿態。而工況2在5級海況下進行分離，雖然分離時間較短，運載器和導彈仍由于波浪沖擊產生較大的傾角。由圖9(c)可知，工況3雖然與工況2的分離環境相同，但由于運載器初始時刻傾斜10°出水，在分離結束后運載器與導彈最終偏轉到垂直姿態。而垂直姿態更有利于導彈的彈道控制，實施全方位攻擊。因此，若能控制運載器以一定角度出水，則在較高海況等級下導彈仍能在分離后獲得較好的初始狀態。

4.2 質心位置

圖10和圖11顯示了各工況下運載器與導彈在分離過程中的質心位置。其中，工況2下由于受波浪推動，運載器與導彈質心均在x方向有較大位移。而由于出水瞬間外部載荷急劇變化，工況1,2,3中運載器質心均在y方向上有輕微晃動。其中工況3由于運載器傾斜出水，受波浪擾動力大，運載器與導彈質心在y方向位移相對較大。此外，各工況下運載器受反推力作用，從0.8 s開始其質心在z方向高度不再上升，轉而落入水中。且同一時刻下，工況3中運載器與導彈質心在z方向位置較工況1與工況2略高。可以推斷，此時波浪對運載器有一定的向上推動作用。

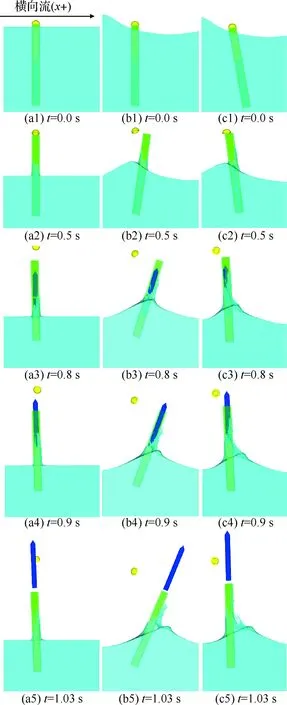
圖9 工況1(a)，工況2(b)，工況3(c)分離狀態圖像序列Fig.9 The image sequence of separating state in working condition 1(a), 2(b) and 3(c)

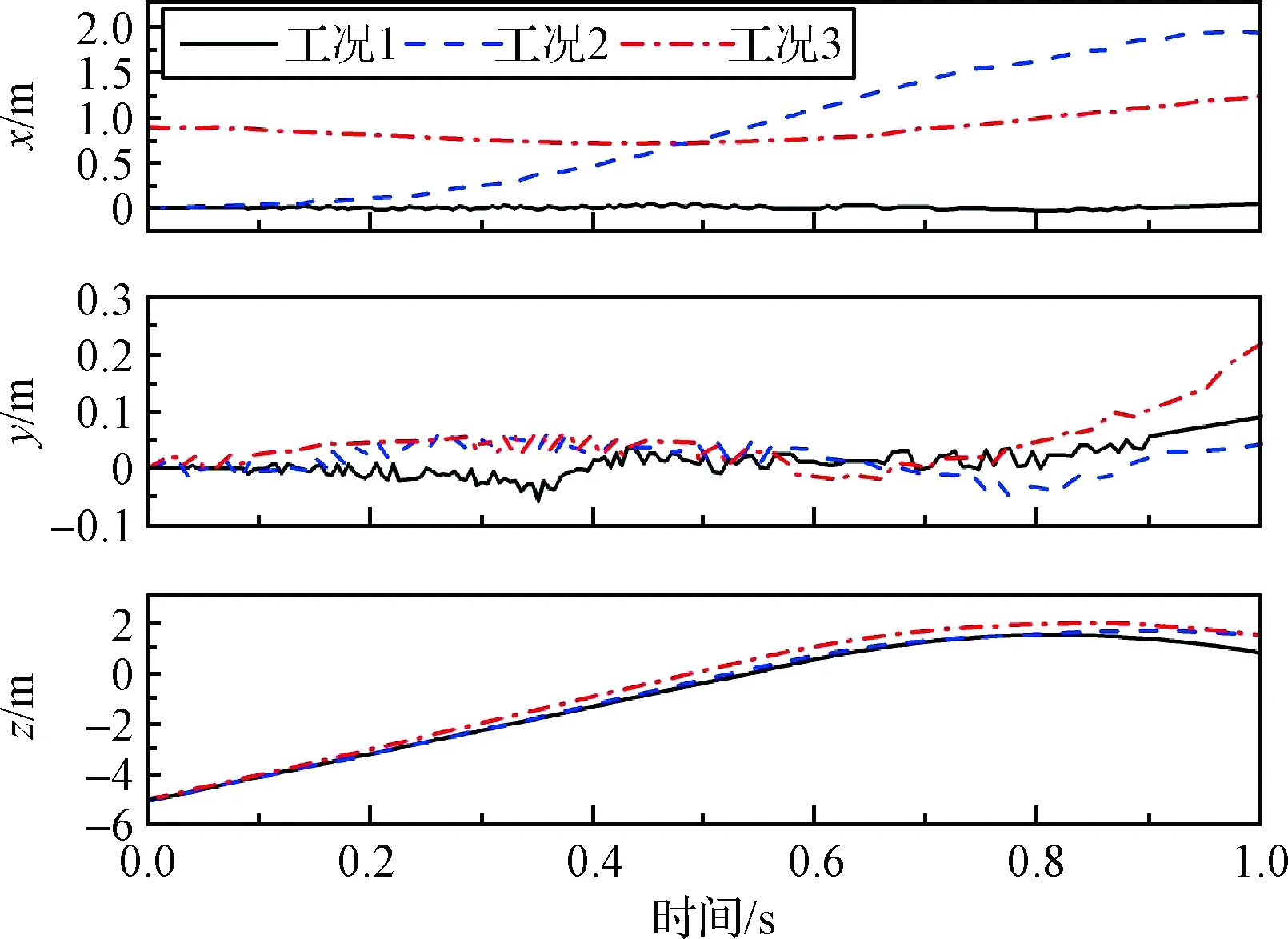
圖10 運載器質心位置Fig.10 Mass center position of launch canister

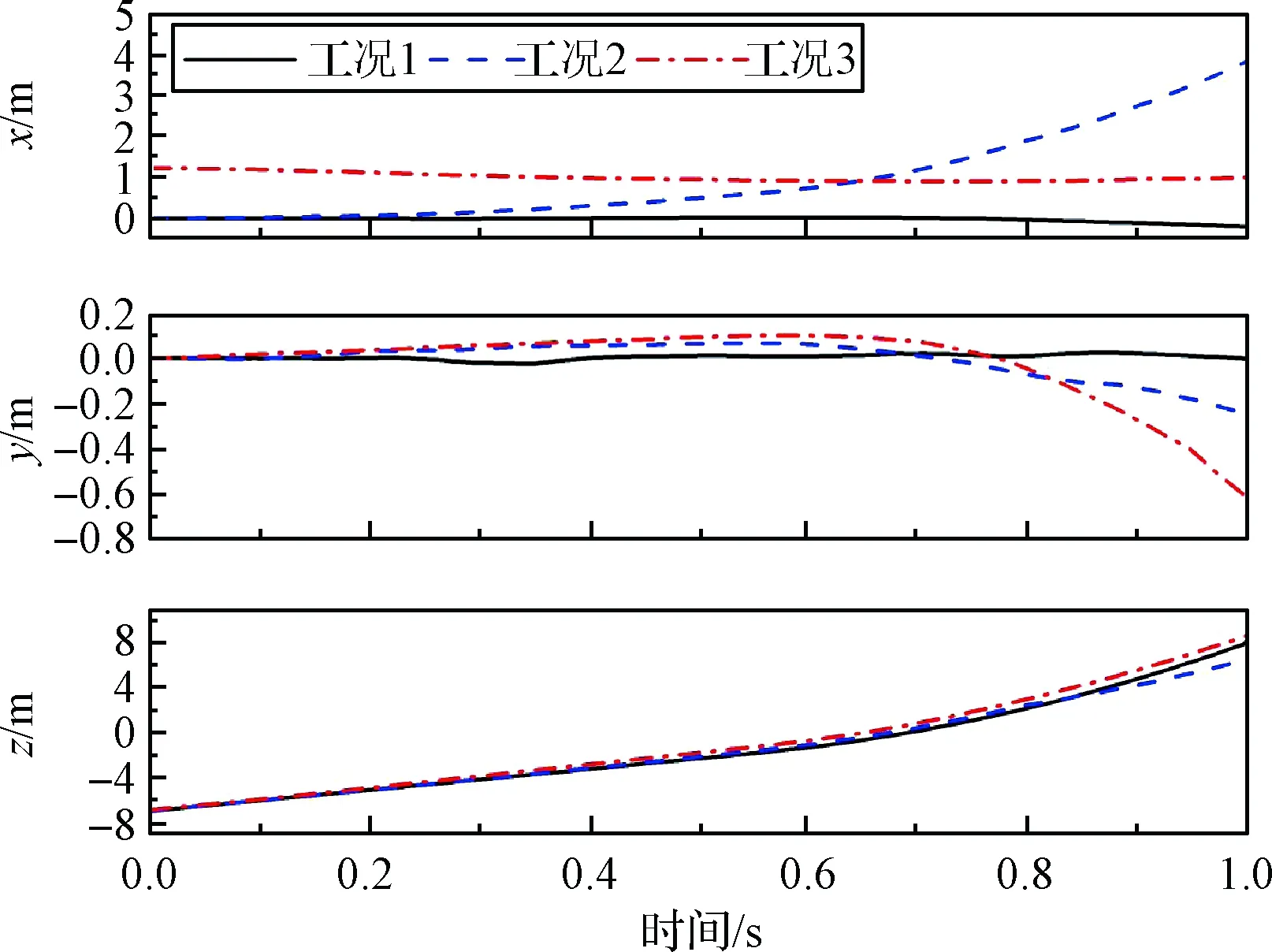
圖11 導彈質心位置Fig.11 Mass center position of missile

4.3 姿態角

圖12和圖13為各工況下運載器與導彈在分離過程中的姿態角。從圖12～13可以看出，工況1下，運載器與導彈各姿態角變化數值較小。而工況2受海面波浪影響，各姿態角顯著增大。其中運載器與導彈的滾轉角φ和俯仰角θ從0.2 s受到波浪沖擊力后逐漸增大，而偏航角ψ從0.5 s導彈點火產生推力開始才逐漸增大。工況3下，由于傾斜出水，受波浪干擾力大，運載器與導彈的滾轉角φ相對較大。而運載器與導彈的俯仰角θ從最開始的-10°偏轉回0°左右。各工況下姿態角的最大絕對值如表3所示。其中工況2下運載器與導彈俯仰角最大絕對值達到22°左右。雖然仍在發射允許的安全范圍內，但若浪高進一步增加，導彈有傾覆的危險。

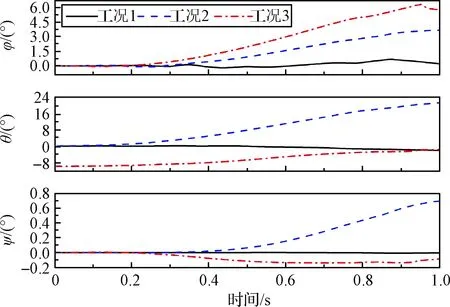
圖12 運載器姿態角Fig.12 Attitude angles of launch canister

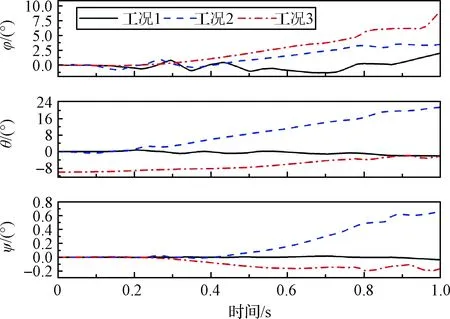
圖13 導彈姿態角Fig.13 Attitude angles of missile

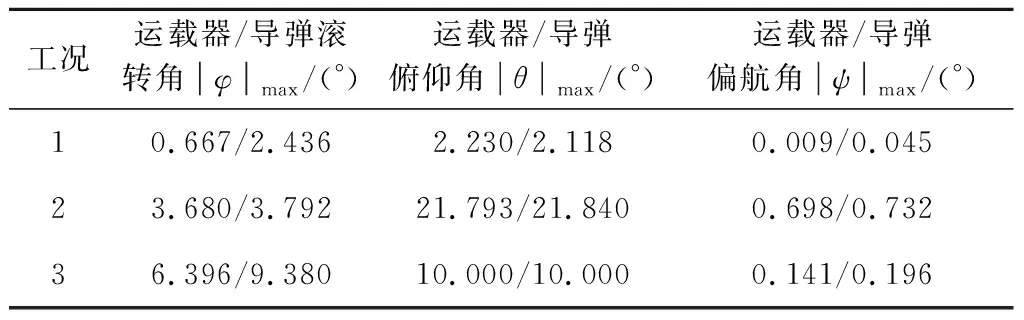
表3 各工況下姿態角最大絕對值Table 3 Maximum absolute value of attitude angles under each working condition

4.4 軸向速度

圖14與圖15為各工況下運載器與導彈在分離過程中的軸向速度。如圖14所示，各工況下，0.5 s即導彈點火前，運載器軸向速度均保持在10 m/s左右。隨后運載器受反推力作用軸向速度降低到-7 m/s左右。整個分離過程中，運載器軸向速度由正到負，最終落入水中。其中工況2由于運載器俯仰角相對較大，受波浪的推動，反向速度增加相對較慢。由圖15可知，導彈受運載器保護，各工況下其軸向速度基本一致。因此，導彈軸向速度不受波浪與出水角度的影響，且導彈分離完成后的軸向速度均達到35 m/s左右，滿足出筒速度的要求。

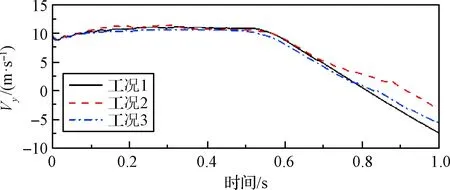
圖14 運載器軸向速度Fig.14 Axial speed of launch canister

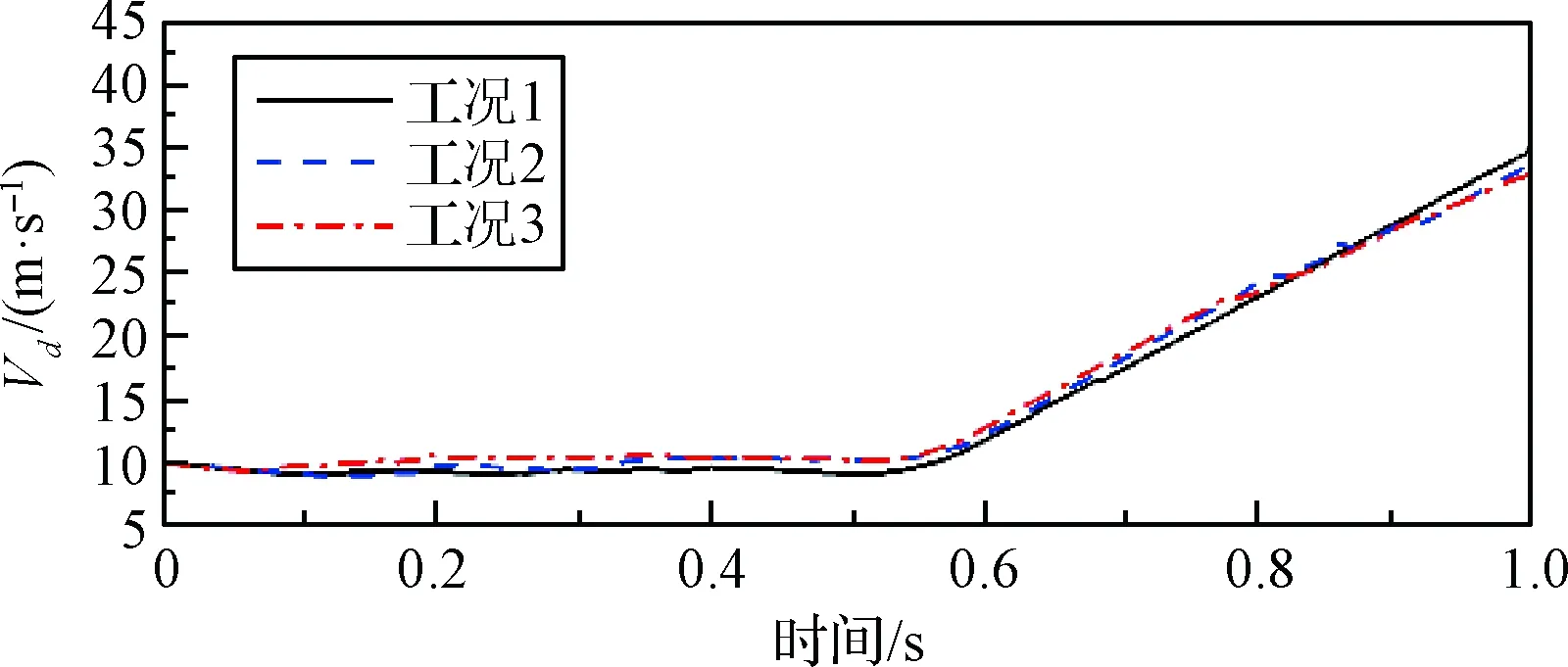
圖15 導彈軸向速度Fig.15 Axial speed of missile

5 結 論

本文建立了自由液面模型與六自由度運動方程，并通過與試驗數據對比驗證了模型的精度。在此基礎上對不同海況以及出水角度下運載器式潛射導彈水面分離的運動特性問題進行了三維數值模擬，主要結論如下：

1)各工況下運載器式潛射導彈均在出水后1.03 s左右完成分離。分離過程中，運載器在y方向上存在輕微晃動。各工況下運載器與導彈的姿態角與軸向速度變化較為穩定，且均在安全范圍內，證明了該種分離方式的優越性。

2)波浪除了推動運載器與導彈在橫向流速的方向產生一定位移外，其影響主要體現在對姿態角散布范圍的增大。其中，增加最為明顯的為俯仰角。在5級海況下，運載器與導彈俯仰角的最大絕對值達到22°。

3)控制運載器以一定角度出水可以保證導彈分離后的相對垂直姿態，但由于傾斜出水受波浪擾動力大，運載器與導彈的滾轉角增大，相應的其在y方向上的位移也有所增大。