一種德州撲克博弈的決策模型

李 軼，彭麗蓉，杜 松，伍 帆，王 森

（1.重慶理工大學兩江人工智能學院，重慶 401135；2.重慶工業職業技術學院大數據與人工智能學院，重慶 401120）

0 引言

機器博弈在人工智能領域一直具有重要的研究價值［1］，根據博弈信息的可知程度，可將其分為完備信息博弈和非完備信息博弈。完備信息博弈是指博弈各方在決策時都完全了解曾經發生的所有博弈信息，例如圍棋、象棋和六子棋等；非完備信息博弈是指博弈各方僅能獲取部分信息，無法獲得對方所有信息，例如軍旗或德州撲克，非完備信息博弈的難點就在于此。在完備信息博弈中，極大極小值算法［2］獲得了巨大成功，而在非完備信息博弈中，由于無法得知部分信息，極大極小值中所需的對狀態的評估過程便無法直接進行，也難以推測對手后續動作，因而使原有博弈算法不能直接應用于非完備信息博弈中。機器學習中的強化學習算法［3］為非完備信息博弈提供了新思路。因此，本文提出一種德州撲克決策模型ACP，并在訓練過程中融入先驗知識，以提高模型訓練效率。將強化學習應用于非完備信息博弈中，是對計算機博弈方法的一次新的探索與嘗試。

1 相關工作

德州撲克的主要研究方法大多是基于博弈論（gametheoretic）或基于知識（knowledge-based）構建的。其中基于博弈論的方法簡單來說就是搜索納什均衡點，德州撲克有很多不同的牌型組合，有限制雙人德州撲克的信息集數量便達到了3.19×1014。兩人、三人及多人德州撲克存在博弈樹規模巨大的問題。針對該問題有兩種解決辦法：①蒙特卡洛樹搜索。不用對博弈樹進行全部搜索，通過犧牲較小的精確度可獲得巨大的性能提升；②牌型抽象化。將博弈過程劃分為兩部分：第一部分包括翻牌前、翻牌和轉牌3個階段，第二部分為河牌階段，如果通過勝率進行抽象化，就可采用整數規劃和狀態空間算法。如文獻［4］使用平滑區間UCT 搜索（Smooth UCT Search）算法，可達到近似納什均衡點。然而，基于博弈論的方法存在的主要問題為：在如此巨大的狀態空間中求解納什均衡需要消耗大量計算資源，同時使用納什均衡策略只能保證自己不輸，因此其期望收益往往很低，在具體博弈場景中實現難度較大。基于知識的方法主要通過記錄職業選手比賽數據，從相關數據中提取出打牌策略［5］，通常可采取窮舉法估算手牌牌力，但窮舉法存在計算量太大的缺陷。蒙特卡洛搜索能解決計算量大的問題，如文獻［6］提出在德州撲克博弈系統中使用強化學習技術，采用蒙特卡洛模擬方法計算勝率作為近似的值函數回報；文獻［7］提出采用基于專家知識的方法建立博弈系統，對職業比賽數據進行特征提取分析，具體特征包括對手下注列表、潛力等。但是，基于知識的方法缺乏比賽數據是德州撲克研究面臨的普遍問題。在數據缺乏的情況下，關鍵在于如何獲得可靠的先驗知識以及如何使用先驗知識解決策略梯度的收斂問題。為此，本文引入一種德州撲克決策模型ACP，以期解決以上問題。

2 德州撲克決策模型ACP

本文根據強化學習框架［8］建立一種德州撲克決策模型ACP。AC 算法包括Actor 網絡和Critic 網絡兩部分，其中Actor 采用基于策略梯度的Reinforce 算法［9］。參數更新公式為：

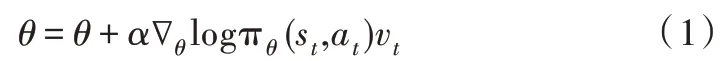
式中，πθ(st,at)表示t 時刻的一種策略，α是學習率，vt、st、at分別表示在t 時刻的獎勵、狀態與動作，參數為θ。在ACP 模型中，Critic 加入先驗知識，即首先通過有監督學習預訓練網絡參數，然后在自博弈中實時存儲對戰數據，再結合已有數據形成系統的知識庫，最后通過損失函數更新整個神經網絡［10］。

整個德州撲克決策模型包含4 個模塊：卷積神經網絡模塊、預測勝率模塊、強化學習模塊、損失函數模塊。決策模型結構與網絡結構如圖1、圖2 所示。

Fig.1 The structure of ACP model圖1 ACP 模型結構

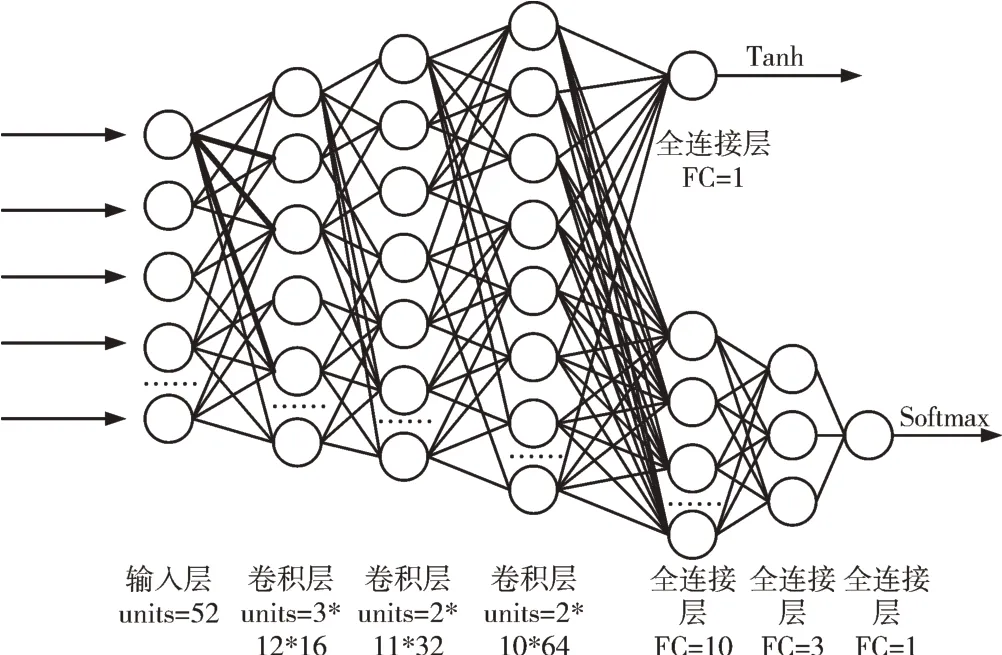
Fig.2 The structure of network圖2 網絡結構

2.1 卷積神經網絡模塊

德州撲克需要52 張牌（王牌除外），本文將52 張牌用一個4*13 的0、1 矩陣表示。該模塊的輸入為4*13*1 的矩陣，4 表示高度（height），13 表示寬度（width），1 表示通道數（filters），中間設置3 個卷積層，卷積核為3*3，步長為1，通道數分別為16、32、64，提取特征得到一個4*13*64 的矩陣。

2.2 預測勝率模塊

提取特征得到矩陣4*13*64，通過壓縮層（Flatten）轉換為1*3 382 的一維數組，再通過激活函數tanh 輸出勝率，勝率值在（-1，1）之間。

2.3 強化學習模塊

將特征提取得到的數據通過3 個全連接神經網絡，神經元個數分別為10、3、1。要注意在第3 層網絡，數據經過一次轉置才能得到想要的輸出形式。通過第1 層網絡得到4*10 的矩陣，第2 層網絡得到4*3 的矩陣，第3 層網絡得到3*4 的矩陣，第4 層網絡得到3*1 的矩陣，再通過soft?max 分類器輸出一個動作，用3*1 的矩陣表示。將該動作輸入環境，勝輸出1，負輸出0，最后將勝負結果輸入損失函數。

2.4 損失函數模塊

該模型采用的損失函數為KL 散度（Kullback-Leibler divergence）與交叉熵（Cross Entropy）之和，如式（2）所示。

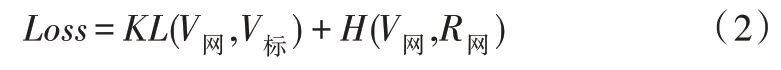
式中，V網表示網絡預測勝率，R網表示動作勝率，V標表示實際勝率，損失函數中包含數據庫，數據庫記錄獲勝的牌型和牌型勝率，產生實際勝率。V網對應q(xi)，V標、R網對應p(xi),KL(V網,V標)能夠提高預測勝率與實際勝率的相似度，H(V網,R網)能夠提高動作勝率與預測勝率的相似度。

交叉熵能夠通過判斷不同信息源之間的兩兩相交程度確定相互支持度，并依據相互支持度確定信息源權重。相互支持度越高，所占權重越大［11］。在離散情況下，具體公式為：

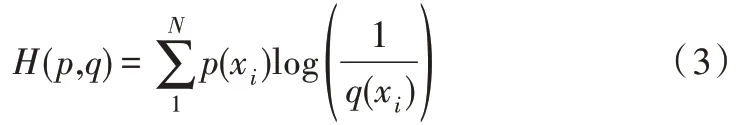
其中，p(xi)、q(xi)表示概率矢量，交叉熵表示概率p(xi)與q(xi)之間的距離，即兩概率分布之間的接近程度。

KL 散度用來度量兩個概率分布的相似程度，可以衡量兩個隨機分布之間的距離。當兩個隨機分布相同時，其相對熵為零。當兩個隨機分布的差別增大時，其相對熵也會增大［12］，如式（4）所示。

3 實驗結果與分析

3.1 實驗設計

數據來源：ACPC（http：//www.computerpokercompetition.org/downloads/competitions/）、中國大學生計算機博弈大賽（http：//computergames.caai.cn/download.html）以及ACP 模型自我對戰產生的數據。

3.1.1 數據預處理

提取勝率和牌型數據進行預處理：

（1）按行讀取，提取每一小局比賽數據，如手牌和公共牌：QsJd|9sKd|Qd6hTc/Ks/Qc 。

（2）根據“/”劃分出每個階段，將手牌、公共牌分別存入一個數組。

（3）循環每個階段：①讀取時默認從小盲位開始，并對變量賦值，小盲賦值為1，否則為0；②對階段變量賦值，如flop 階段=｛1 0 0｝，turn 階段=｛010｝，river 階段=｛001｝；③讀取對應階段公共牌，存在A、K、Q 則相應變量賦值為1，否則為0；④判斷是否有2 張相同牌值出現，出現一對牌時相應變量賦值為1，否則為0；⑤判斷是否存在3 張牌值相同的牌，參考步驟④；⑥A、K、Q 在公共牌中出現的次數統計，參考步驟④；⑦統計花色相同的牌數量，參考步驟④。

（4）存儲處理得到的數據到表中。

3.1.2 實驗流程

（1）打牌程序生成2 個手牌，隨機輸出公告牌（從flop階段開始記錄），然后輸出勝負結果，將手牌信息及勝率記錄到表中。

（2）使用表中數據預訓練網絡參數。

（3）將完全相同的兩個模型相互對弈，一個更新參數，一個不更新參數。訓練一定局數后，將更新模型的參數復制給不更新的模型，再進行對弈。通過模型間不斷的參數交替，反復對弈，得到最終版本。

（4）將模型最終版本與其他3 個版本進行對弈，得出結果。

3.2 損失函數收斂對比

圖3 為普通PG 模型損失函數走勢圖，該模型采用與ACP 模型類似的網絡結構，但不融入先驗知識。PG 模型和ACP 模型訓練100 000 局，PG 模型損失函數值在2.25～2.26 之間振蕩幅度較大，隨著訓練局數的增加，損失函數也沒有明顯的收斂趨勢，模型在沒有先驗知識的指導下，收斂性較差。圖4 中ACP 模型的損失函數值在10 000 局后呈現較明顯的收斂趨勢，振蕩幅度減小。因此，融入先驗知識的ACP 模型具有更好的收斂性。

Fig.3 Trend of PG model loss function圖3 PG 模型損失函數走勢

Fig.4 Trend of ACP model loss function圖4 ACP 模型損失函數走勢

3.3 ACP 模型與其訓練版本對比

圖5 為ACP 模型自博弈訓練最終版本與其它3 個版本智能體分別對弈5 000 局的平均收益對比圖（平均收益=當前贏得的總籌碼÷當前完成局數），版本1 為一個只會跟注、不會棄牌的撲克智能體，版本2 是單純根據勝率決策的智能體，版本3 是采用ACP 模型自博弈訓練了100 000局后的智能體。隨著訓練局數的增加，ACP 模型在先驗知識的指導下，通過損失函數不斷更新神經網絡，決策勝率也逐步提高。實驗結果表明，ACP 模型最終版本與其他3個版本相比具有一定優勢，但不能保證持續獲得更大的收益。

Fig.5 The game benefits result of ACP model vs 3 agents圖5 ACP 模型與其他3 個版本對局收益情況

4 結語

本文從基于知識和基于博弈論兩個方面簡單介紹了德州撲克的主要決策方法，并根據強化學習框架設計了一種德州撲克決策模型。該模型采用AC 算法，融入了先驗知識，一定程度上提高了強化學習算法的收斂速度。該模型與其他3 個版本對局時有較好表現，缺點是ACP 模型的決策不能針對特定對手獲得極限收益。此外，該模型存在高方差、收斂速度慢等缺陷。因此，如何將A3C 算法運用于該模型中，對網絡參數進行分布式訓練，同時提高訓練效率，是后續研究重點。