軸承故障深度對系統振動響應的影響

何付軍

（火箭軍士官學校，山東 青州 262500）

研究軸承故障參數對系統振動的影響，首先需要弄清楚滾動體在進入故障和離開故障時的系統振動變化，為了更清楚的揭示這一變化規律，本節從最常用的矩形故障模型入手，在單轉子的右端引入相同的軸承外圈故障，通過計算得出轉子右端加速度的波形圖，如圖1所示。

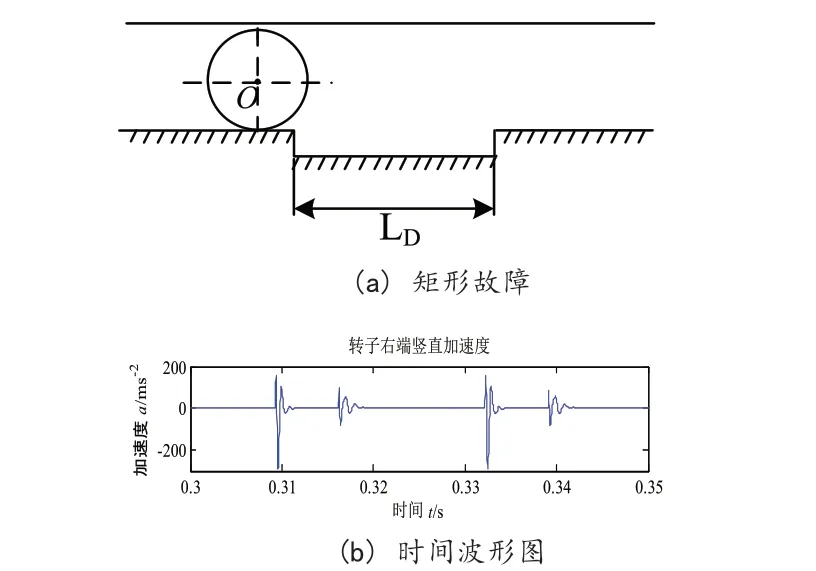
圖1 不同故障形貌的外圈故障及其響應

從圖1中可以看出，非規則故障相比于矩形凹槽，在加速度波形圖上所反映的最大的差別在于滾動體通過故障區域時的波形變化，矩形凹槽故障所表現的是一條直線，而非規則故障所表現的是一條非規則曲線，由圖可知矩形故障所顯示的雙沖擊現象非常明顯，但是與實際情況存在較大差別。下圖能夠很好地反映滾珠通過故障時轉子右端加速度的變化。

1 軸承故障深度的影響

設轉子轉速為600r/min，軸承外圈滾道存在故障且故障周向寬度LD為3mm，軸承故障的深度h分別為0.1mm、0.3mm、0.5mm時，不同類型故障所對應轉子右端豎直加速度隨時間變化的曲線，滾動體在進入和離開故障的瞬間都產生了較明顯的加速度變化，由于故障形貌的差異，導致加速度時間波形存在較大差異，隨著深度的增加，轉子右端加速度峰值顯著增大，說明，隨著故障深度增加，滾動體對于滾道的沖擊力明顯變大。

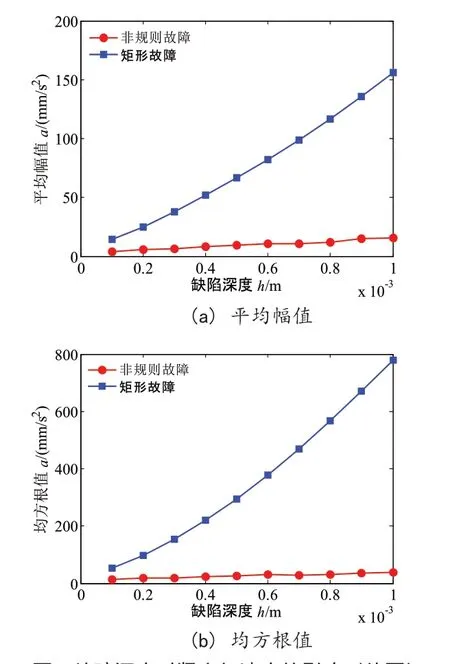
圖2 故障深度對豎直加速度的影響（外圈）

圖2中（a）、（b）為系統響應的平均幅值、均方根值隨故障深度的變化曲線。從圖中可以很明顯看出，隨著故障深度增加，系統振動的有量綱幅值也是逐漸增大的，然而矩形故障的變化較非規則故障而言變化尤其明顯，原因是在進行矩形故障引起的振動計算時，假設了滾動體進出故障的時候是一個瞬時過程，而實際情況為滾動體進入故障時是漸變的過程，因此非規則軸承故障所對應的幅值變化較為 平緩。

設右端軸承內圈滾道出現故障且故障的周向寬度LD為3mm，深度h分別為0.1mm、0.3mm、0.5mm時不同類型故障時轉子右端的加速度時域波形圖，滾動體進入和離開故障區域的瞬間產生了沖擊脈沖，加速度發生了明顯變化。與外圈故障一樣，隨著深度的增加，轉子右端加速度峰值顯著增大，說明，隨著故障深度增加，滾動體對于滾道的沖擊力明顯變大。相比外圈故障而言，內圈故障引起的振動沖擊更劇烈。圖3（a）、（b）為系統響應的平均幅值、均方根值隨故障深度的變化曲線。從圖中可以很明顯看出，隨著故障深度增加系統振動的幅值也是逐漸增大，同樣，相比于矩形故障而言，實際非規則故障引起的加速度振動變化較為平緩。

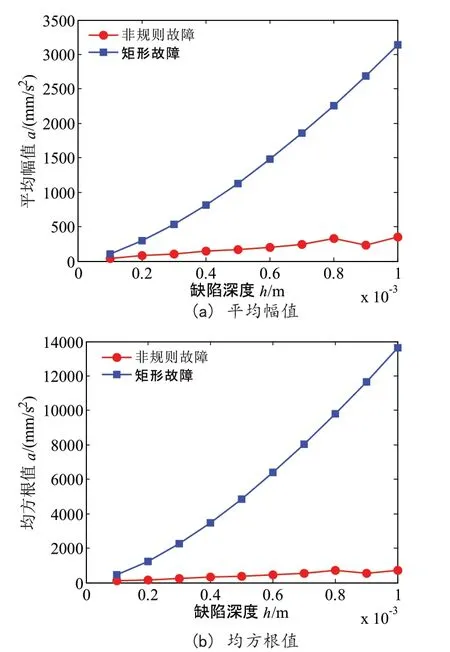
圖3 故障深度對豎直加速度的影響（內圈）

2 結論

分別計算了系統軸承在內圈含有矩形故障和非規則故障情況下，所產生的振動響應。分析了故障的深度對于系統振動的影響，結果表明，在內圈含有故障的情況下，相同程度的矩形故障所產生的沖擊要明顯高于非規則故障，對于內圈而言故障深度對系統振動影響十分明顯，隨著故障深度的增加，矩形故障所產生的沖擊強度顯著增加，非規則故障產生的沖擊強度總體上增加。