在界面處引入原子混合層結構的熱導性能分析

呂荒蕪

（華北電力大學（保定）能源動力與機械工程學院，河北 保定 071003）

0 引言

自20世紀40年代第一代計算機問世至今，大量電子元件的制造技術都達到了納米級別。納米材料被廣泛應用于電子器件制造行業，例如計算機的芯片CPU、量子級聯激光器和場效應晶體管等。高精度帶來高運行效率的同時，也會導致更高的熱功率，設備運行中產生的大量熱量不僅會影響工作效率，還會有降低使用壽命的風險，因此熱管理問題的研究刻不容緩。

納米結構的多樣化和易操作性為熱管理提供了廣闊的發展前景[1-2]。由于納米結構部件和設備中存在較高的表面積體積比，材料界面處的熱傳遞通常主導著整體的熱行為，它們是熱載體的散射中心，可以通過調整它的物理特性來控制器載流子的分散強度。因此深入了解界面熱導的性能，對研究納米結構材料的熱傳輸具有重要意義[3]。

1 研究背景

向結構中引入多層復合原子混合層是1種能夠有效提高系統界面熱導的方法[4]。研究表明，界面的原子在某些特定的排布狀態下能夠促進界面處的熱交換。Tian Zhiting等人將格林函數方法與Laudauer方程相結合，詳細闡述了原子混合引起的界面紊亂是如何增加界面處的聲子輸運和界面熱導[5]。Carlos和Rouzbeh[6]利用格林函數法研究了不同固體材料界面上的一系列熱導，他們的研究顯示，在平滑的界面中引入單層的原子混合層總是能夠增強界面的熱導，但是根據原子晶體結構的不同，熱導的增加也會有所不同，熱導增量的變化可以達到1個數量級。盡管學者們已經在構造使界面熱導最大化的原子混合層方面取得了許多進展[7-8]，然而目前對混合層的厚度以及溫度變化對界面熱導的影響的分析仍然缺乏統一和定量的構建模式。

受上述研究啟發，該文在2種不同材料的界面處構建原子混合層，采用分子動力學方法對結構進行模擬，討論了原子混合層的數量以及溫度對界面熱導的影響。此外，研究人員還詳細計算了2種結構的聲子態密度和聲子參與率，分析了不同結構下系統界面處聲子散射的機制。該研究的主要目的是找到合適的原子混合層構建方式，從而改善聲子頻率失配界面處的熱輸運。

2 模型構建

如圖1所示，研究人員用Atomsk軟件構建了理想的Si/Sn界面結構，考慮到計算的精度和系統的運算能力，研究人員將結構的總原子數設置為5120，Si/Sn理想界面處于整個納米結構的中間位置，界面左側為Si原子，右側為Sn原子。研究表明，當分子動力學模擬采用周期性邊界條件對導熱系數進行計算時，在橫截面積為不小于3×3個原胞的情況下，橫截面積對導熱系數的影響可以忽略。因此，在該研究中，研究人員將橫截面面積設置為4 UC×4 UC，x、y、z3個方向上的原胞以4 UC×4 UC×40 UC（Unit Cell）的形式進行排列。研究人員將以Si/Sn理想界面為基礎，采用替換原子的方式在理想界面處引入原子混合層納米結構。

圖2是理想Si/Sn界面處引入Si/Sn原子混合層的納米結構，研究人員在圖1的基礎上，以界面為中線，在保證模型總長度不變的情況下向界面處引入1～10層的原子混合層，混合層中的Si、Sn原子數目各占50%，并且隨機排布。

3 計算方法

所有的非平衡分子動力學模擬都是在LAMMPS軟件環境下運作的，由于Stillinger-Weber（SW）勢函數已經被證實能夠較為精確地解釋硅基納米結構的熱力學特性和界面熱導，因此該模擬選取了SW勢函數描述Si-Si、Ge-Ge、Sn-Sn、Si-Ge、Sn-Ge以及Si-Sn之間的力關系。模擬計算熱性質示意圖如圖3所示，為了防止與外界產生熱量交換，研究人員固定了2個外壁，并將該區域內粒子的速度設置為0，然后分別將緊鄰邊界區域設置為熱源和熱匯，從而建立溫度梯度。為了節約計算資源，研究人員將模擬的時間步長設為0.001 ps。在非平衡分子動力學模擬的第一階段，使系統處于壓力為0、溫度為300 K的環境下，采用等溫等壓系綜（NPT）對系統進行弛豫。在系統模型達到完全弛豫后，在X和Y方向上施加了周期性邊界條件，并在Z方向上采用了固定邊界條件。為了使系統的能量分布處于均勻的狀態，研究人員讓系統繼續在正則系綜（NVT）下弛豫2 ns，系統再次達到平衡后，模擬將在微正則系綜（NVE）下繼續運行10 ns，與此同時，每隔1000個時間步長記錄1次原子信息。

圖1 理想Si / Sn界面結構

圖2 理想Si/Sn界面引入原子混合層結構

圖3 NEMD 模擬計算熱性質示意圖

界面熱阻R可以表述為溫度梯度ΔT與熱通量Jz的比，如公式（1）所示。

溫度梯度ΔT是通過對于溫度曲線進行線性擬合獲得的，熱通量Jz如公式（2）所示[9]。

式中：E為能量；t為模擬時間；A為橫截面積；hot bath為熱源。

根據傅里葉導熱定律，熱導率k如公式（3）所示。

考慮橫截面積為A、長度為d的1個長方體材料，其熱導K與熱導率k的關系如公式（4）所示。

實際分析中更常用的是單位面積的熱導，通常用符號G表示。求解該長方體材料單位面積的熱導如公式（5）所示。

聲子態密度（PDOS）是表征系統中聲子活動的強大工具。它是根據所有原子的速度自相關函數（VACF）的傅立葉變換計算得出，如公式（6）所示。

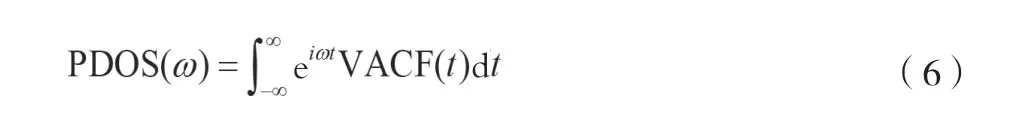
式中：PDOS（ω）為振動頻率為ω時的總聲子態密度。

VACF（t）可以表示為如公式（7）所示。

式中：vi（t）為粒子i在時間t下的速度矢量；N為系統中的原子數； 為系綜平均。

聲子參與率（PPR）是了解聲子輸運的另一種有效方法，它可以用來定量描述聲子局域化效應。PPR如公式（8）所示。

式中：N為系統中總原子數；為頻率為的第i個原子的聲子態密度。

4 結果與討論

為了研究薄膜厚度對跨界面熱傳輸的影響，研究人員讓原子混合中間層的厚度在0個、2個、4個、6個、8個和10個原子層之間變化。圖4為不同原子混合層厚度下系統的界面溫度分布圖。從圖4中可以觀測到Si/Sn界面處的溫度出現了急劇下降的情況，該情況可以直接歸因于界面熱阻的影響。值得注意的是，不同厚度的原子混合中間層，其界面處處的溫度分布具有不同的形狀。隨著中間層厚度的增加，界面處溫度降的變化趨勢較為一致。

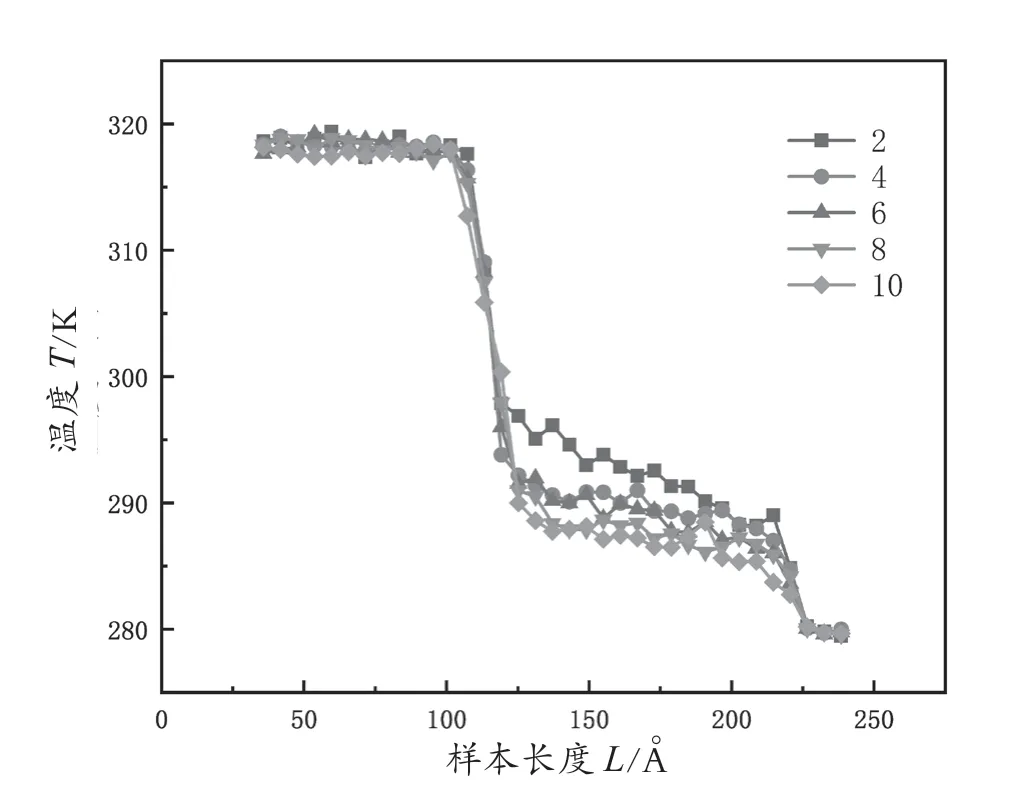
圖4 引入原子混合層系統的界面溫度分布

為了分析原子混合中間層的厚度對熱導率的影響，研究人員計算了不同混合層數下系統的熱導。在分子動力學模擬過程中，將溫度設置為300 K，樣本長度設為23.844 nm（238.44 A°）。模擬結果如圖5所示，從圖5可以看出，在中間層原子層數從0層變化到2層的過程中，系統的界面熱導大約提升了31.6%。而隨著原子層數從2層變化到10層，熱導就逐漸下降。原子層數達到10層后，引入中間層的系統的界面熱導比平滑界面的熱導降低了29%。原子混合層為2層時，系統的熱導達到最大值。模擬結果表明，在2種高度不匹配的材料之間插入原子混合層，可以顯著改善跨Si/Sn界面的熱傳輸。

圖5 界面熱導隨混合層厚度變化圖

研究人員計算了系統中界面熱導與溫度之間的關系，計算結果如圖6所示。結果表明，隨著溫度的升高，所有參與模擬的系統的界面熱導都先呈上升的趨勢，然后呈下降的趨勢。當溫度升至300 K時，引入2個原子層的原子混合層的系統的熱導達到最大值。隨著溫度的升高，原子的振動能量會增加，由于在聲子散射Umklapp的過程中，聲子散射會增強;因此，隨著溫度繼續升高，系統的界面熱導會進一步降低。

圖6 不同混合層數界面熱導隨溫度變化圖

針對引入了2層原子混合層的系統，分別選取界面以及兩側的Si、Sn原子部分進行聲子態密度計算（PDOS）。由于研究人員發現界面兩側固體表面和中間層中的原子主要以低于20 THz的頻率振動，因此只取了頻率小于20 THz的態密度。繪制出的PDOS如圖7所示。此外，研究人員還繪制了不同混合層的系統態密度圖（如圖8所示）。

從圖8中可以看出，內部的聲子態密度（PDOS）受厚度變化的影響較小。隨著系統內混合層厚度的增加，混合層PDOS中的聲子模式會略微向低頻方向遷移，并且PDOS曲線的頻寬會呈現出增大的趨勢。圖6中，原子混合層的PDOS與Sn結構PDOS的重疊面積大于Si結構和Sn結構PDOS的重疊面積。較大的PDOS重疊面積表示非彈性聲子散射會增加界面處的熱傳輸[10]。

圖5中，引入雙層原子混合層結構的熱導明顯高于單層原子混合層結構的熱導。研究人員猜測熱導的提高是因為中間層與Sn結構DOS的重疊面積有所提高。對單原子層或兩原子層的中間層來說，兩側的原子結構和中間層相互作用主導著層中原子的運動。隨著中間層厚度的增加，層與層之間的相互作用變得越來越重要。因此，雙層原子混合層的DOS頻寬變得稍微寬一些（如圖9所示）。單層原子混合層的DOS相對雙層來說更銳利和狹窄，這應該歸因于其強大的約束效應。較寬的DOS增大了中間層DOS與兩側原子結構DOS的重疊面積，增強了原子混合層與Si原子結構和Sn原子結構之間的非彈性聲子散射，從而略微提高了界面處的聲子熱輸運[10]。然而，同時彈性界面散射可能會隨之減少。因此，熱導在2原子層的厚度處達到最大值，然后熱導隨厚度增加而減小（如圖5所示）。

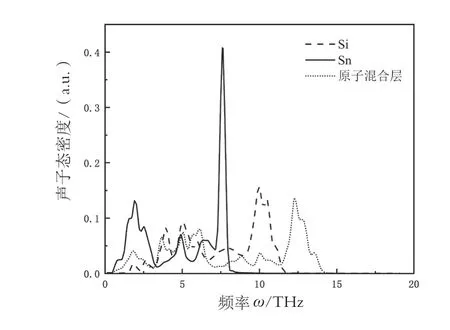
圖7 2層混合層系統態密度圖

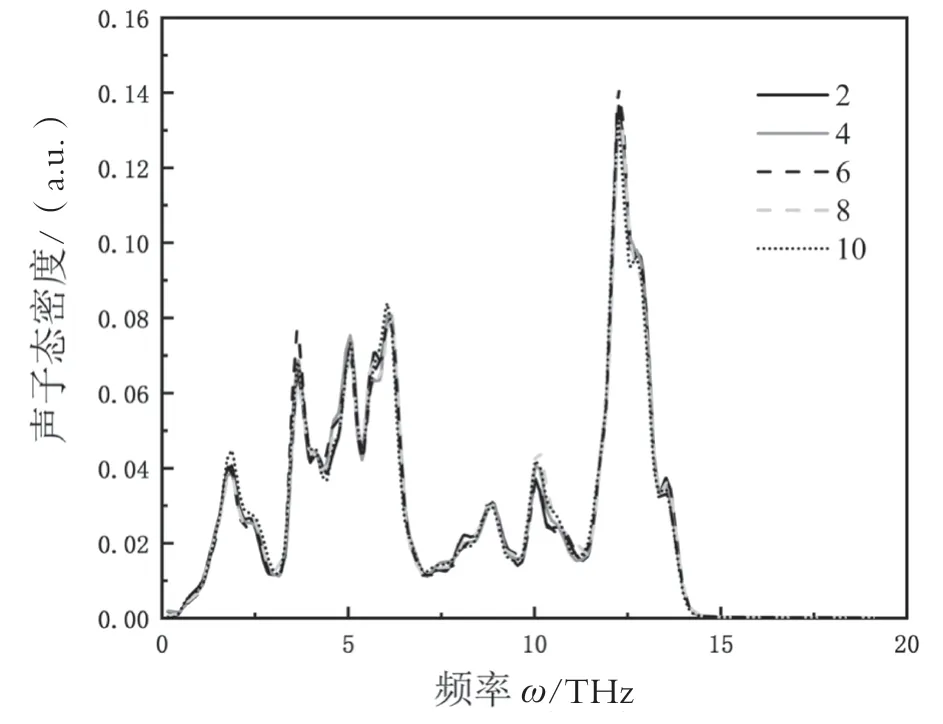
圖8 不同混合層系統態密度圖

圖9 雙層以及單層混合層態密度圖

綜上所述，可以得出結論，隨著原子混合層厚度的增加，系統的DOS不會改變太多。中間層的DOS分布與Sn結構DOS之間的重疊面積會出現略微增加的情況。研究人員認為彈性界面散射不可能是引起2層和單層中間層之間的熱導增加的原因。因此，將界面熱導的增加歸因于非彈性聲子界面散射的微弱增加。隨著引入界面的原子混合層層數增大，熱導在層數高于2之后逐漸降低。研究人員認為該現象可以歸因于界面處的彈性散射與非彈性散射之間的競爭。盡管根據圖6和圖8已經可以證明，引入雙層原子混合層能夠增加非彈性界面散射，從而增加熱傳導；但是隨著中間層厚度的增加，界面處的彈性散射逐漸減小。非彈性散射的增加已經不再能與彈性散射的減小相抗衡，從而出現了熱導在中間層厚度超過2層之后減小的現象。

為了探究聲子活動（尤其是聲子的局域化程度）以及聲子對不同系統熱導的影響，研究人員使用公式（8）計算了聲子的參與率。聲子參與率可以測量給定模式下的原子比率，并可以用O （1/N）和O （1）分別表示局域化和非局域化下的聲子模式。聲子參與率可以詳細地展示每種聲子模式的局域化信息。圖10分別展示了當系統界面處原子混合層數為2、6和10時的聲子參與率，參與模擬的樣本長度為23.844 nm，溫度設置為300 K。研究人員認為PPR＜0.4時，證明聲子發生了局域化現象。結果表明，無論考慮低頻聲子還是高頻聲子，隨著原子混合層厚度的增加，系統的PPR逐漸降低。隨著混合層厚度的增加，越來越多的聲子顯示出聲子局域化的特征。而聲子對熱傳輸的貢獻主要來自非局域化聲子，而不是局域化的聲子[11]。與預期結果相同，由于存在聲子局域化的現象，因此包括10個原子混合層的系統的界面熱導通常比其他2個系統都要小。

圖10 混合層聲子參與率

5 結語

該文在納米結構的界面處構建了1種能夠有效提高界面熱導的原子混合層結構，與光滑界面相比，該界面的熱導提高了31.6%。采用非平衡分子動力學方法，分別模擬不同尺寸和不同溫度下該結構的熱導的變化，并利用聲子態密度以及聲子參與率對該結構能夠大幅度提高熱導的原因進行分析。為高散熱硅基納米材料的開發研究提供了一定的指導，對高散熱半導體材料的制備和發展有重要意義。