XGBoost啟發的雙向特征選擇算法
王 麗, 王 濤, 肖 巍, 劉兆賡, 李占山
(1. 長春工業大學 計算機科學與工程學院, 長春 130012; 2. 吉林大學 人工智能學院, 長春 130012; 3. 吉林大學 計算機科學與技術學院, 長春 130012)
特征選擇是機器學習領域中的一個重要問題, 可通過縮小特征維度提高模型的精度及運行速度, 減少運行時間. 在尋找最優特征子集過程中, 通過結合一些搜索策略去除冗余特征與不相關特征, 目的是在給定的泛化誤差下選擇維度最小的特征子集, 或者選擇具有K個特征的最佳特征子集, 使其在原始樣本上產生最小的泛化誤差[1].
由于特征的選取方式與評價方式不同, 因此特征選擇方法又分為過濾式方法、 包裹式方法及嵌入式方法[2]. 過濾式方法通常依賴于數據的固有屬性, 如方差、 熵、 相關性等估計特征子集的重要程度, 不依賴于特定的學習器, 通常速度較快并具有可伸縮性[3]. 包裹式方法通過一些已有的機器學習算法評估所選的特征子集, 評估過程依賴于這些機器學習算法并與之不斷交互, 通常產生的結果較好[4]. 嵌入式方法將特征選擇過程融入學習過程中, 通過優化預先設計好的目標函數搜索最優特征子集, 并在學習過程中刪除對分類結果影響較小的特征, 保留良好特征[5].
由于搜索空間會隨著特征個數的增加呈指數級增長, 所以在分類問題中的特征選擇是NP難問題. 對于包含n個特征的問題, 其搜索空間會有(2n-1)種可能的結果[6-7]. 目前, 對特征選擇方法已有許多研究成果, 在分類問題中, 不同搜索策略產生的最優特征子集也不同, 因此也可分為窮舉法、 隨機方法以及基于啟發式的特征選擇方法等. 窮舉法試圖完全搜索特征空間以找到一個能正確區分所有類別的最小特征集合. 但當數據的特征個數較多時, 在時間和空間上很難計算和評估所有的特征子集, 因此在包含大量特征的數據集中很少用窮舉法. 基于啟發式的特征選擇算法有定向搜索算法、 分支界限法、 最優優先搜索算法等[8]. 這些算法能在保持模型精度的同時找到最佳的特征子集[9]. 這類算法的優點是具有良好的時間復雜性, 特別是基于演化計算的方法由于其超強的全局搜索能力在特征選擇問題中受到廣泛關注[10]. 如文獻[11]提出了通過基于特征的熵信息生成切割點序列表, 尋找最佳切點組合進行特征選擇的改進離散化粒子群優化算法; 文獻[12]給出了以特征為頂點、 以特征相關性為邊構造無向圖, 并將無向圖導出為最小生成樹, 通過處理最小生成樹的方法進行特征選擇.
集成學習是解決機器學習問題的重要方法之一[13], 本文受基于決策樹的集成學習中極端梯度提升算法(XGBoost)的啟發, 提出一種新的特征選擇算法BSXGBFS(bidirectional search based on XGBoost for feature selection). 該算法首先考慮將XGBoost算法中用于構建集成樹模型的指標選為特征選擇問題中單個特征的重要性度量指標, 然后提出一種新的雙向搜索策略更好地權衡如何使用多個特征重要性進行特征選擇, 最后給出新算法BSXGBFS理論上的時間復雜度上界.
1 預備知識
1.1 特征選擇問題
特征選擇問題可描述為: 對于給定N個樣本D個維度特征的數據集DataSetN×D, 特征選擇任務就是從D個維度特征中選取d個特征(d≤D), 使得目標函數J(S)取最大值, 其中SubDataSetN×d是DataSetN×D的一個特征子集, 簡記為S. 優化目標J一般為模型的分類準確率、 維度縮減率或二者的結合. 即特征選擇的目的是通過選取特征數量盡可能少的特征子集S使得目標函數J(S)最大化. 求解特征選擇問題時, 通常采用如下二進制編碼方式將第i次選取的d維特征子集擴展到D維:
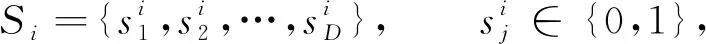
(1)
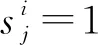
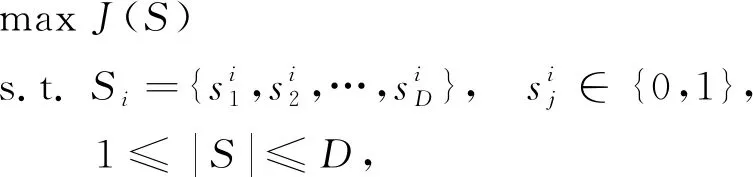
(2)
其中|S|表示在特征子集S中選取的特征數量.
1.2 XGBoost算法
極端梯度提升算法XGBoost是一種基于樹的Boosting算法[14]. XGBoost算法相比于傳統的梯度提升決策樹算法, 創新性地利用了損失函數的二階導數信息, 使得XGBoost算法能更快收斂, 保證了較高的求解效率, 同時還增大了可擴展性, 因為只要一個函數滿足二階可導的條件, 則在適當的情形下該函數便可作為自定義的代價函數而被使用. XGBoost算法的另一個優點是其借鑒了隨機森林算法中的列抽樣方法, 進一步降低了計算量和過擬合. 目前, XGBoost算法被廣泛應用的原因不僅在于其訓練后的模型表現好、 速度快, 能進行一些數據規模較大的計算, 而且其既能解決分類問題, 還能很好地處理回歸問題[15].
XGBoost算法可表示為
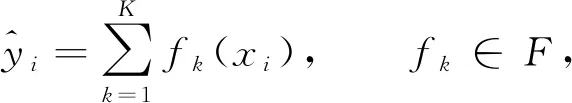
(3)
其中K表示樹的棵數,F={f(x)=ωq(x)}(q:m→T,ω∈T)表示模型的函數空間,fK(xi)表示第i個樣本在第K棵樹中的分類結果. 由XGBoost算法的表達式可見, 該模型是迭代殘差樹的集合, 每次迭代時都會增加一棵樹, 每棵樹通過學習前(N-1)棵樹的殘差, 最終構成由K棵樹線性組合而成的模型.
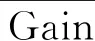
對任意結構確定的樹, 有
其中C是所有樹用于產生節點時使用的特征集合, GainC是每棵樹用C中特征分割后產生的增益值, CoverC是樹用C中的特征分割時落在每個節點的樣本個數.
2 BSXGBFS算法設計
2.1 雙向搜索策略
為能在特征選擇問題中算法性能更好, 本文結合經典的前向特征選擇和后向特征選擇方法的優勢, 提出新的雙向搜索策略, 步驟如下:
1) 前向添加過程. 首先, 設空集為初始狀態的特征選擇目標集合, 并將候選子集中的全部特征根據式(4)~(6)中的一個重要性衡量標準A1進行評價并排序. 其次, 依次從中選擇重要性高的特征添加到目標集合中, 并對加入新特征后的特征集合進行評價, 保留能提高分類準確性的特征. 經過若干次執行后, 得到初步的目標特征子集. 這種方法的優勢是根據已經評價好的特征重要性度量結果做啟發式, 能給出一個特征選擇的方向, 即初步選定一個較好的搜索空間.
2) 后向篩除過程. 將步驟1)中得到的初步目標特征子集再根據式(4)~(6)中的另一個特征重要性指標A2或A3評價后的結果篩除一個最不重要的特征, 進一步提高分類準確性. 經過若干次執行后, 最終得到一個分類準確率較高且特征數目較少的特征子集. 這種方法能保證通過另一個特征評價指標進一步綜合衡量出單個特征的實際重要程度, 進而保證刪除冗余特征.
2.2 BSXGBFS算法描述
BSXGBFS算法進行特征選擇主要包含兩個過程: 構造迭代樹模型和雙向搜索策略. XGBoost算法中定義的整體損失函數為
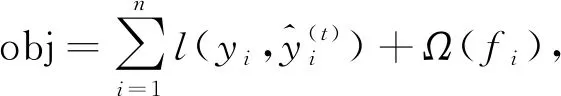
(7)
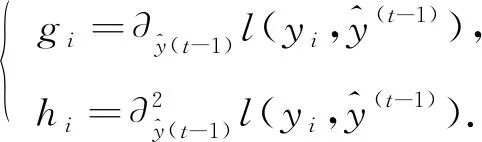
(8)
為降低樹分割后的損失, 根據各子節點的權值進一步計算不同特征作分割點后帶來的增益Gain, 有
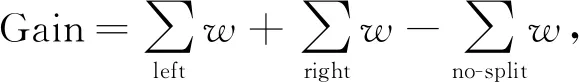
即作分割點的特征產生的增益可表示為: 該特征節點左右分支的子節點總權值之和與用該特征作分割點前總權值之差.
先根據式(4)~(6)分別計算3種特征重要性, 并得到對應的特征重要性評價集合A1,A2,A3, 然后從這3個集合中選擇2個, 作為執行雙向搜索策略的特征評價集合. 在實際操作中, 會有6種可能的排列結果, 因此可利用多核CPU的優勢一次性并行完成計算, 縮短計算時間, 并使結果趨于最優.
BSXGBFS算法的偽代碼如下.
算法1BSXGBFS算法.
輸入: Original feature setA;
輸出: Objective feature setO;
O← ?
depth ← 0
Initialization the three measures of feature importance Fcount, AvgGain, AvgCover
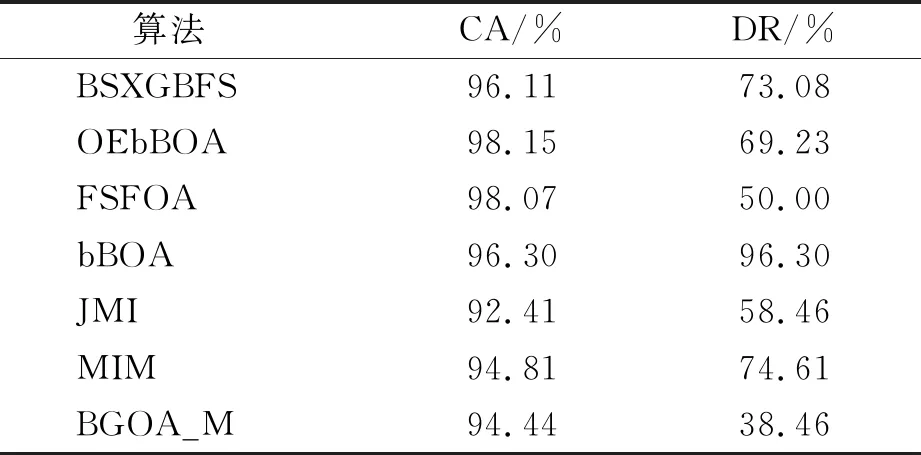
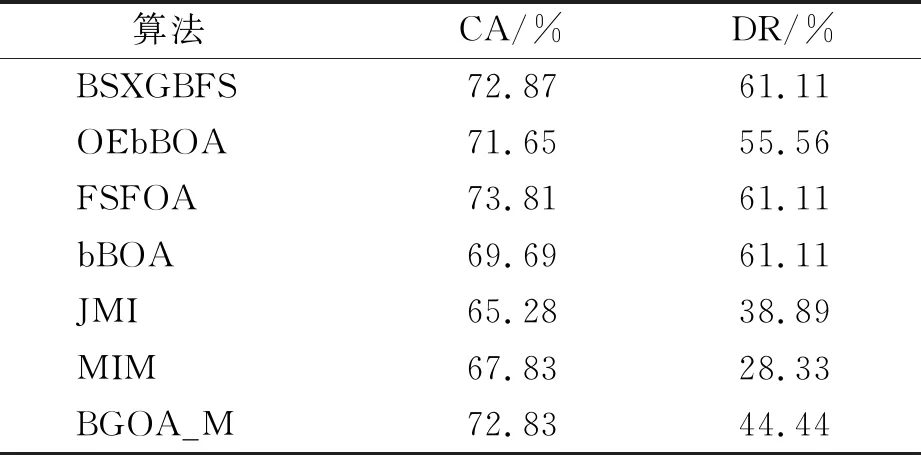
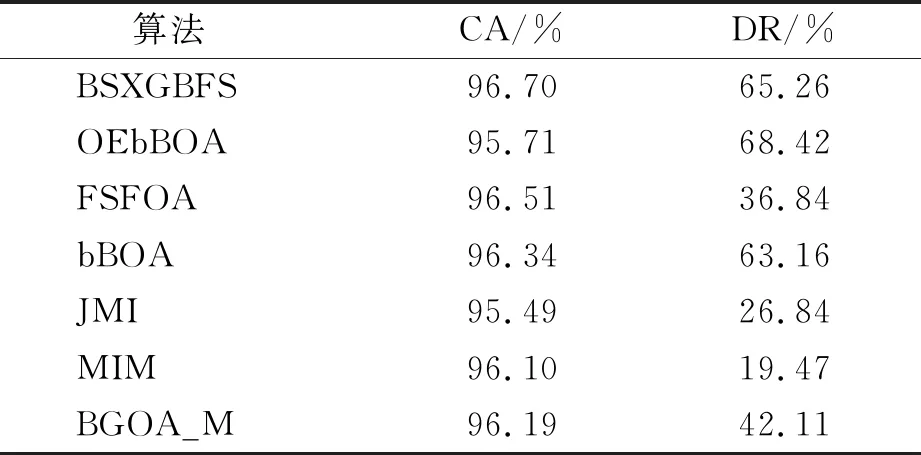
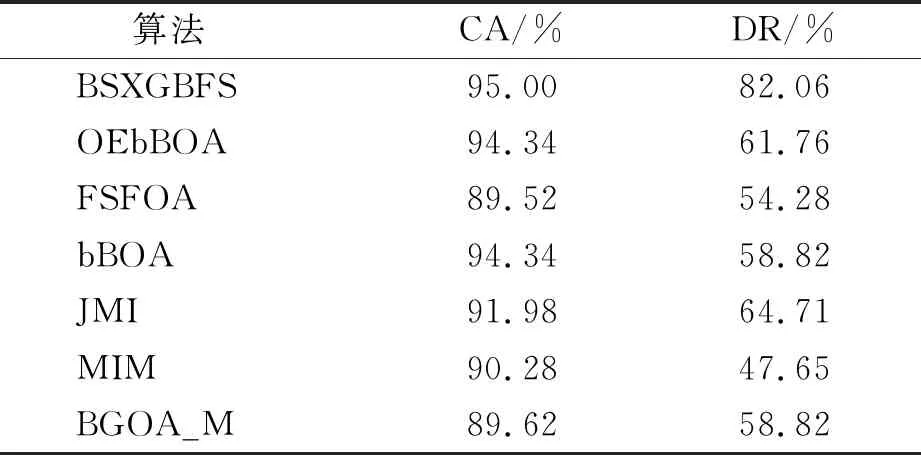
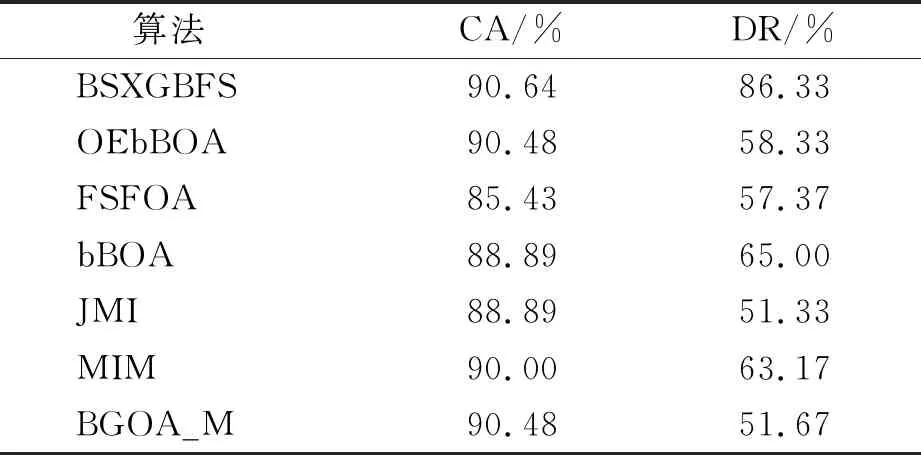
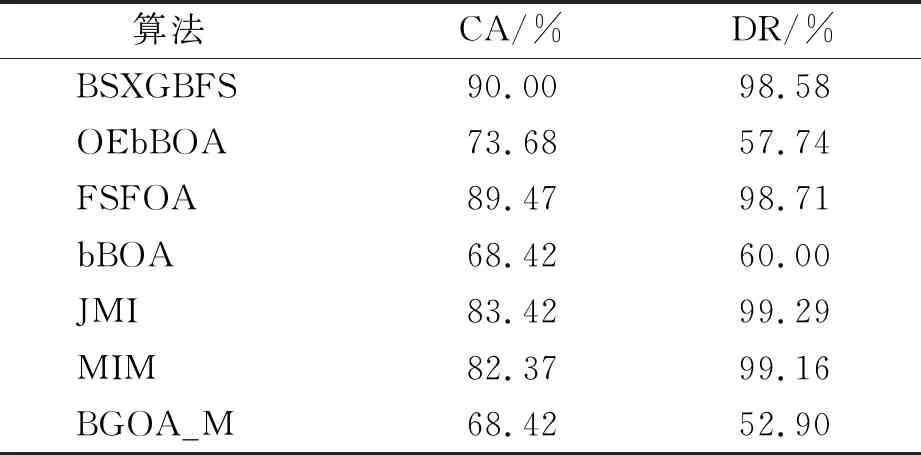
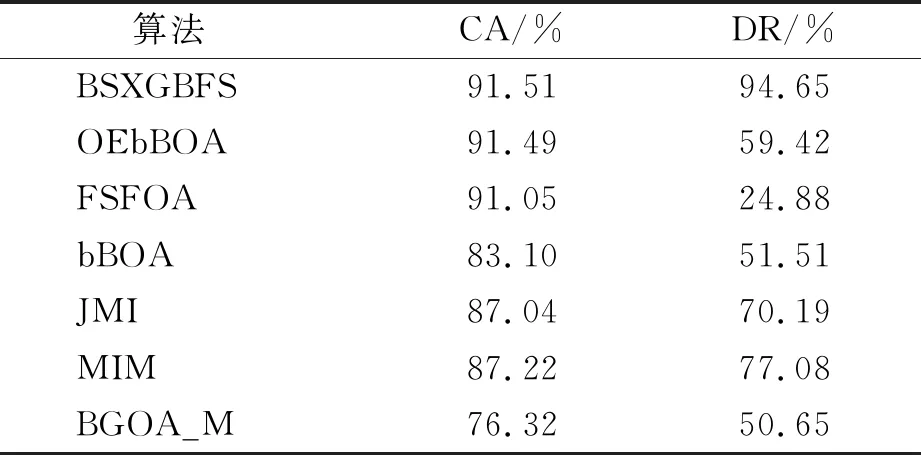
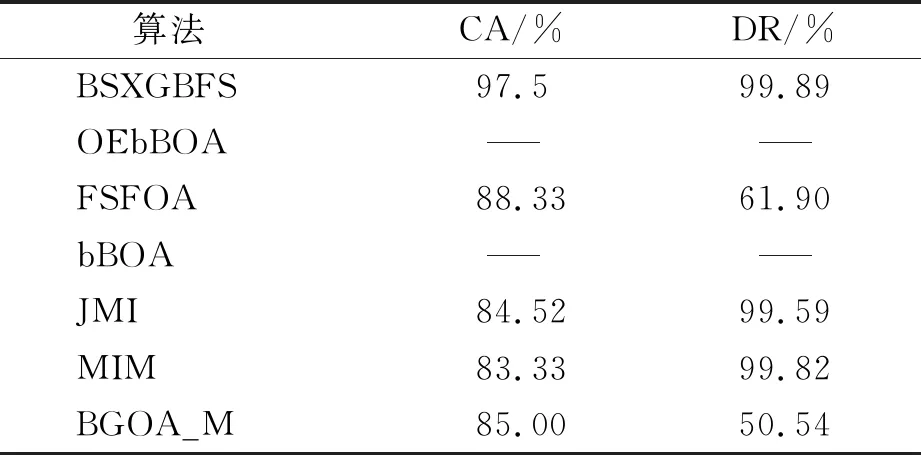
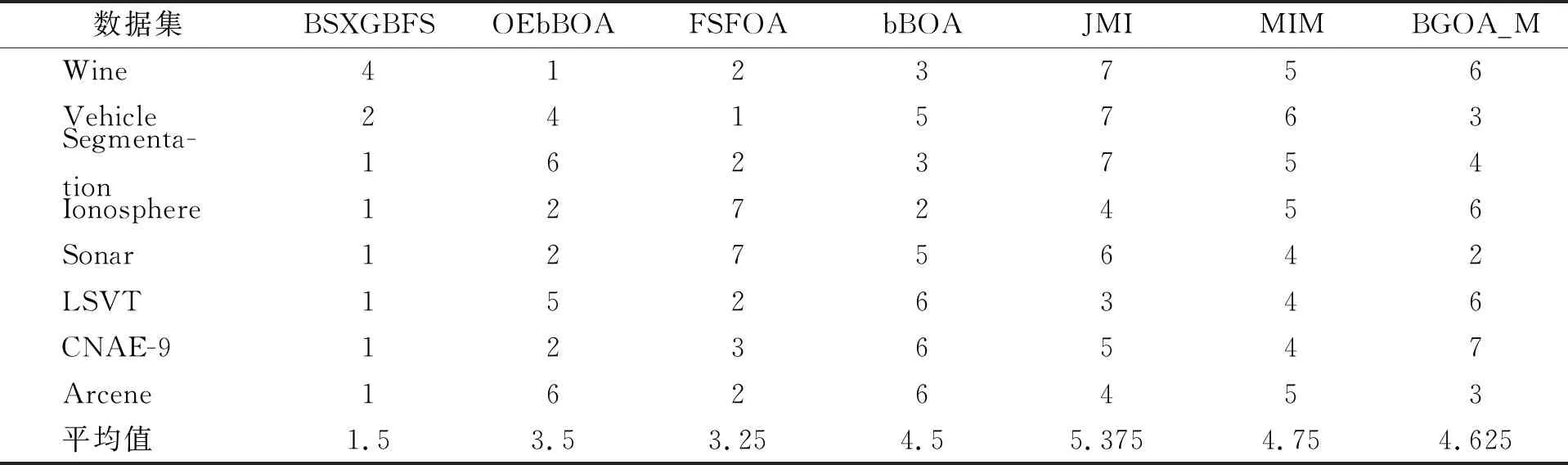
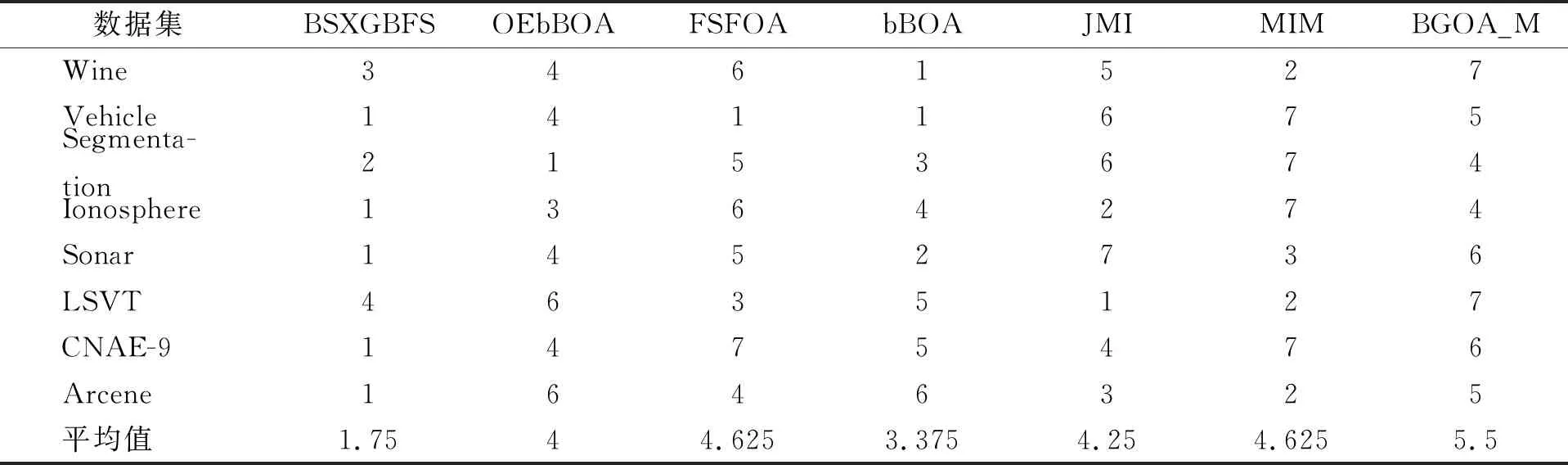
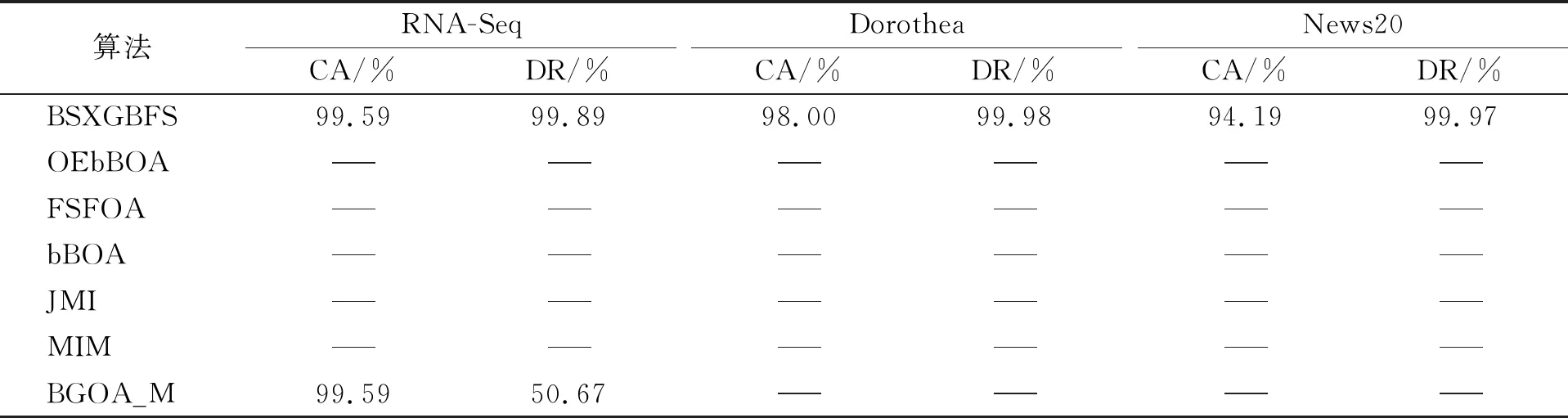
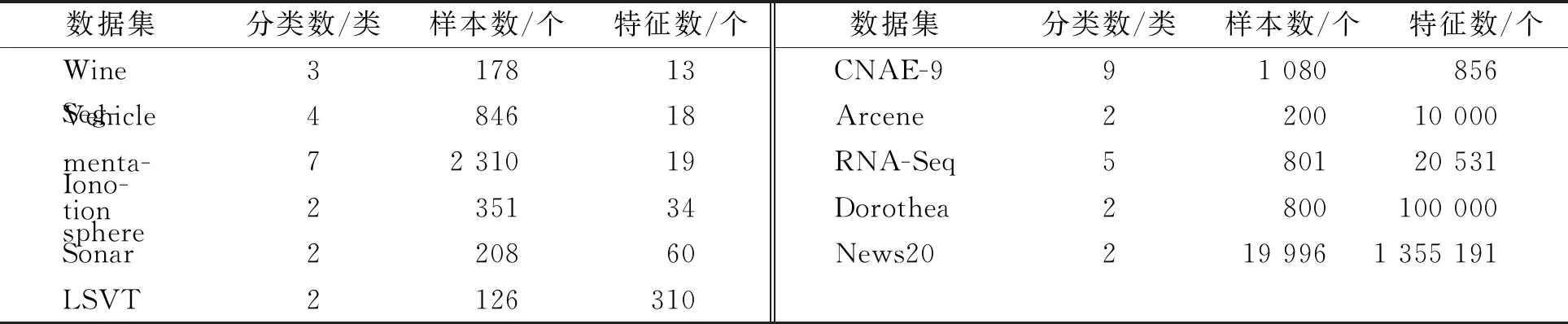
while depth for a inAdo Calculus the best feature segmentation pointak Generate left child node and right child node depth ← depth+1 Update ensemble model for tree in ensemble model do for node of tree do Calculate gain and cover generated by node Fcount ← Fcount+1 Gain ← Gain+gain Cover ← Cover+cover forainAdo AvgGain ← Gain/Fcount AvgCover ← Cover/Fcount GetA1from sortingAin descending order according to Fcount GetA2from sortingAin descending order according to AvgGain GetA3from sortingAin descending order according to AvgCover Select two set fromA1,A2andA3randomly, then rename them asB1andB2 ReverseB2 forbiinB1do O′←O∪bi ifJ(O′)>J(O) then O←O′ forbjinB2do ifbjinO O′←O-bj ifJ(O′)>J(O) then O←O′ returnO. O(MNlgN+MNKD+mlgm+2mT). 實驗選擇目前應用最廣泛的UCI(UCI machine learning repository)數據庫中的11個覆蓋低維到超高維的標準數據集, 各數據集信息列于表1. 實驗選擇多策略二元蝴蝶優化特征選擇算法(OEbBOA)[16]、 基于森林優化算法的特征選擇算法(FSFOA)[17]、 基于蝴蝶優化算法的特征選擇算法(bBOA)[18]、 使用聯合互信息策略的特征選擇算法(JMI)[19]、 使用互信息最大化策略的特征選擇算法(MIM)[19]、 基于二元蝗蟲優化算法的特征選擇算法(BGOA_M)[20]作為與本文算法的對比算法. 實驗中全部實驗代碼使用Python 3.6實現. 實驗平臺處理器為AMD Ryzen 7 1700, 內存容量32 GB, 硬盤容量2 TB. 表1 UCI的數據集信息 采用多數研究中常用的分類準確率(classification accuracy, CA)與維度縮減率(dimensionality reduction, DR)做實驗結果分析的性能衡量指標[21-22]: CA=CN/AS, (9) DR=(AF-SF)/AF, (10) 其中CN表示分類正確的樣例數, AS表示全部樣例數, AF表示特征總數, SF表示進行特征選擇后的特征數. 采用KNN(K=1)作為評價分類準確率的基分類器. KNN分類器具有易實現且參數較少, 能更好地反映特征選擇算法自身性能的特點, 因此使用KNN測試特征選擇算法的性能, 并用于對比實驗[18-22]. 數據集的劃分均采用70%的樣例作為訓練集, 30%的樣例作為測試集. 實驗結果列于表2~表12. 表2 BSXGBFS及其對比算法在Wine數據集上的測試結果 表3 BSXGBFS及其對比算法在Vehicle數據集上的測試結果 表4 BSXGBFS及其對比算法在Segmentation 數據集上的測試結果 表5 BSXGBFS及其對比算法在Ionosphere數據集上的測試結果 表6 BSXGBFS及其對比算法在Sonar數據集上的測試結果 表7 BSXGBFS及其對比算法在LSVT數據集上的測試結果 表8 BSXGBFS及其對比算法在CNAE-9 數據集上的測試結果 表9 BSXGBFS及其對比算法在Arcene 數據集上的測試結果 表10 BSXGBFS及其對比算法在10 000維內的數據集上分類準確率測試結果 表11 BSXGBFS及其對比算法在10 000維內的數據集上維度縮減率測試結果 表12 BSXGBFS及其對比算法在高維數據集上的測試結果 由表2~表12可見, 對于10 000維以內的數據集, BSXGBFS算法無論是在分類準確率還是維度縮減率上, 都存在較高的競爭力, 甚至在Ionosphere,Sonar,CNAE-9,Arcene這4個數據集上, 分類準確率和維度縮減率性能在全部對比算法中都達到了最優. 因此, BSXGBFS算法不存在如OEbBOA,FSFOA,BGOA_M等基于演化計算的特征選擇算法需要過多犧牲維度縮減率換取分類準確率的問題, 而是在確保分類準確率的前提下兼顧了維度縮減率, 也進一步驗證了采用特征重要性評價作啟發式的合理性. 由表12可見, 在使用RNA-Seq,Dorothea,News20這3個數據集對BSXGBFS算法進行極限測試的過程中, 發現BSXGBFS算法具有可以進一步計算10 000維以上高維數據集的能力, 甚至在10萬維Dorothea數據集和100萬維News20數據集上都具有可計算性. 實驗結果表明, BSXGBFS算法的性能與預期相符, 不僅在中低維數據集上的性能良好, 而且在高維數據集上也具有可計算性. 綜上所述, 本文受集成學習算法XGBoost的啟發, 提出了一種適用范圍更廣, 能處理高維數據的特征選擇算法BSXGBFS. 對比實驗結果表明, BSXGBFS算法不僅在中低維數據集上相比于其他算法更具競爭力, 同時在高維甚至超高維數據集上也具有良好、 可靠的計算能力.2.3 時間復雜度分析
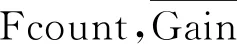
3 實驗設計與分析
3.1 實驗設計
3.2 實驗分析