基于EEMD的列車車輪多邊形故障診斷方法

李鳳林，杜紅梅，巫忠書，陳翔宇，樊懿崴

基于EEMD的列車車輪多邊形故障診斷方法

李鳳林，杜紅梅，巫忠書，陳翔宇，樊懿崴

（成都運達科技股份有限公司，四川 成都 611731）

多邊形故障作為車輪常見的故障形式之一，不僅會增大列車的振動和噪聲、降低列車乘坐舒適性，還會加劇輪軌相互作用力，導致車輛和軌道部件過早出現疲勞失效，對列車安全穩定運行造成不良影響，因此對車輪多邊形故障進行診斷具有重要意義。本文根據多邊形故障軸箱振動響應提出了基于總體經驗模態分解（EEMD）的車輪多邊形故障診斷方法。其核心是對軸箱振動加速度進行EEMD分解，然后通過相關能量（CN）自動提取車輪多邊形故障的IMF分量，并通過包絡譜分析診斷車輪是否存在多邊形故障，最后通過頻譜分析診斷車輪多邊形階次。通過仿真數據和線路試驗數據對該方法進行驗證，驗證結果表明，該方法能有效診斷出車輪多邊形故障。

車輪多邊形；總體經驗模態分解；相關能量；故障診斷

隨著我國軌道交通的快速發展，輪軌磨耗引起的車輪多邊形問題愈發嚴重。列車運行時，多邊形故障會激發輪軌間的沖擊作用力，不僅會導致車內振動和噪聲增大、降低列車乘坐舒適性和穩定性，還會降低車輛和線路關鍵部件的疲勞壽命，危及列車運行安全[1-6]。因此，開展車輪多邊形故障診斷的研究具有重要的理論意義和工程應用價值。

目前，軌旁監測法是車輪多邊形故障診斷中最常用的方法[7-9]，然而該模式無法在長距離服役過程中對車輛運行狀態進行實時監測，因此國內外學者通過采集軸箱振動加速度識別車輪多邊形故障。李湙番[10]提出了基于改進希爾伯特-黃變換（Hilbert-Huang Transform，HHT）的車輪多邊形故障診斷方法，并通過仿真和實驗數據驗證了該方法的有效性；徐曉迪[11]提出了基于同步壓縮短時傅里葉變換（Short-Time Fourier Transform，STFT）的自適應共振解調方法，并實現了車輪多邊形故障診斷；孫琦[12]提出了基于welch譜估計的一種固定階次車輪多邊形故障診斷，并用在線監測數據驗證了該方法的有效性；陳博[18]提出了基于改進的集合經驗模態分解（Modified Ensemble Empirical Mode Decomposition，MEEMD）和遺傳算法支持向量機（Genetic Algorithm-Support Vector Machine，GA-SVM）的列車車輪多邊形故障識別方法，通過篩選出主要IMF（Intrinsic Mode Function，固有模態函數）分量并計算包絡譜熵，最后輸入GA-SVM中進行訓練和識別，最后識別出車輪多邊形故障。

總體經驗模態分解（Ensemble Empirical Mode Decomposition，EEMD）可以自適應地對信號進行分解，得到不同尺度下的IMF分量，并且能抑制間歇性噪聲、脈沖干擾導致的模態混疊現象[13]。據此，本文提出一種基于EEMD的車輪多邊形故障診斷方法，通過相關能量（Correlated Energy，CN）篩選車輪多邊形對應的IMF分量，并通過包絡譜分析確定該車輪是否存在多邊形故障，最后通過頻譜分析確定車輪多邊形階次。

1 基于EEMD的車輪多邊形故障提取方法

1.1 經驗模態分解（EMD）

經驗模態分解（Empirical Mode Decomposition，EMD）是美國國家宇航局N.E.Huang等[14-15]提出的自適應信號處理方法，其核心是將原信號分解為頻率由高到低的若干個固有模態函數和一個殘差，其中每個IMF表示原信號在不同尺度下的局部特征。N.E.Huang等定義IMF為[14]：

（1）IMF的極值點和過零點數目相等或相差一個；

（2）IMF的極大值和極小值確定的上、下包絡線均值為零。

EMD分解流程如下[14]：

（1）對信號()的極大值和極小值進行插值，分別得到信號的上下包絡線，然后計算上下包絡線的均值1()；

（2）原始信號減去均值曲線1()，得到第一個分量：

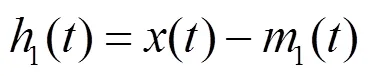
如果1()滿足上述IMF定義，則將1()作為第一個IMF分量；若不滿足，則對1()重復步驟（1）和步驟（2），直到出現第一個IMF分量。

（3）從原信號()中分離出IMF1，對剩余信號()-IMF1繼續進行分解，得到多個IMF分量，直到剩余信號()是一個單調函數。最后將原信號()分解為個IMF分量和一個剩余信號()：

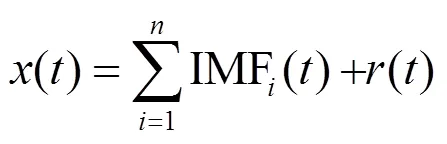
1.2 總體經驗模態分解（EEMD）

然而，當信號中存在間歇性噪聲或脈沖干擾時，EMD分解得到的IMF分量會出現頻率混疊現象，具體表現為一個IMF分量中包含多個尺度信號，或相近尺度信號存在于多個IMF分量中。模態混疊嚴重時，會導致EMD分解結果失效。為改善此問題，N.E.Huang等在EMD分解基礎上提出了添加輔助噪聲的信號分解方法——總體經驗模態分解[13]，其步驟如下：

（1）在原信號()中多次加入相同幅值的白噪聲：

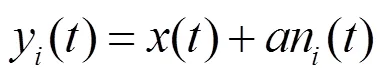
式中：為白噪聲幅值，一般取原信號標準差的0.1～0.2倍；n()為白噪聲（＝1,2,3,…,），表示對原信號加噪的次數；y()為第次加噪的信號。

（2）分別對加噪聲的多組信號進行EMD分解，得到對應的IMF：

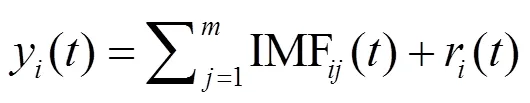
式中：IMF()為第次加噪信號的第個IMF分量；為IMF分量個數；r()為第次加噪信號的分解殘差。

（3）對多組IMF進行平均，得到最終的IMF分量為：

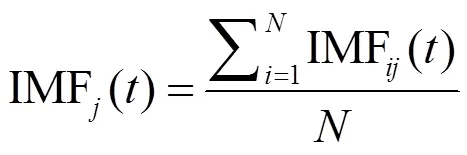
上述過程中，EEMD通過對原始信號添加噪聲，改善原始信號中間歇性噪聲或沖擊脈沖導致的信號不連續，最后通過對多組IMF集成平均抑制白噪聲帶來的干擾。所以EEMD既能抑制模態混疊，又能提高信號分析的精確度。

1.3 車輪多邊形主要IMF選取

EEMD將軸箱振動信號分解成一組IMF分量，每個IMF分量包含了不同尺度的局部特征。為了更容易診斷出車輪多邊形故障，需要篩選出車輪多邊形故障對應的IMF分量，以提高信號信噪比。

多邊形故障表現為低頻振動信號，因此通常選低頻段的IMF分量作為車輪多邊形故障分量，但實際情況下，信號中的趨勢項或一些虛假分量也存在于低頻段的IMF分量中，因此直接選用低頻段IMF分量可能選到與車輪多邊形故障無關的分量。

因此，為了自適應篩選出車輪多邊形故障對應的IMF分量，本文提出了車輪多邊形故障診斷指標——相關能量（CN），定義其為：

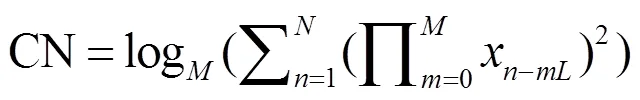
式中：x為輸入信號；為信號長度；為移位階次；為車輪轉動一周對應采樣點數，即輸入信號的移位長度，可以通過式（7）得到。

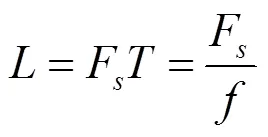
式中：F為信號采樣頻率，Hz；為車輪轉動頻率，Hz；為車輪轉動一周的時間，s。

相關能量通過移位累乘，可以將與車輪轉頻相關的周期性信號保留，并抑制白噪聲或其他與車輪轉頻無關的周期性成分，因此可以用該指標識別車輪多邊形故障的IMF分量。當車輪多邊形信號分解后的某個IMF分量的相關能量值較大，則該IMF分量中保留了較多車輪多邊形信號成分，將該IMF分量做包絡譜分析和頻譜分析，即可確定該車輪是否存在多邊形故障以及多邊形故障階次。

1.4 基于EEMD的車輪多邊形故障提取流程

如圖1所示，基于EEMD的車輪多邊形故障提取流程具體為：

（1）對車輪多邊形振動數據計算EEMD，得到若干個IMF分量；

（2）根據式（2）計算各IMF分量的相關能量CN，選取最大相關能量IMF分量作為車輪多邊形故障的主要分量；

（3）對主要分量做包絡譜分析，確定該車輪是否存在車輪多邊形故障；

（4）如果該車輪存在多邊形，則對主要分量做傅里葉頻譜分析，確定車輪多邊形階次。

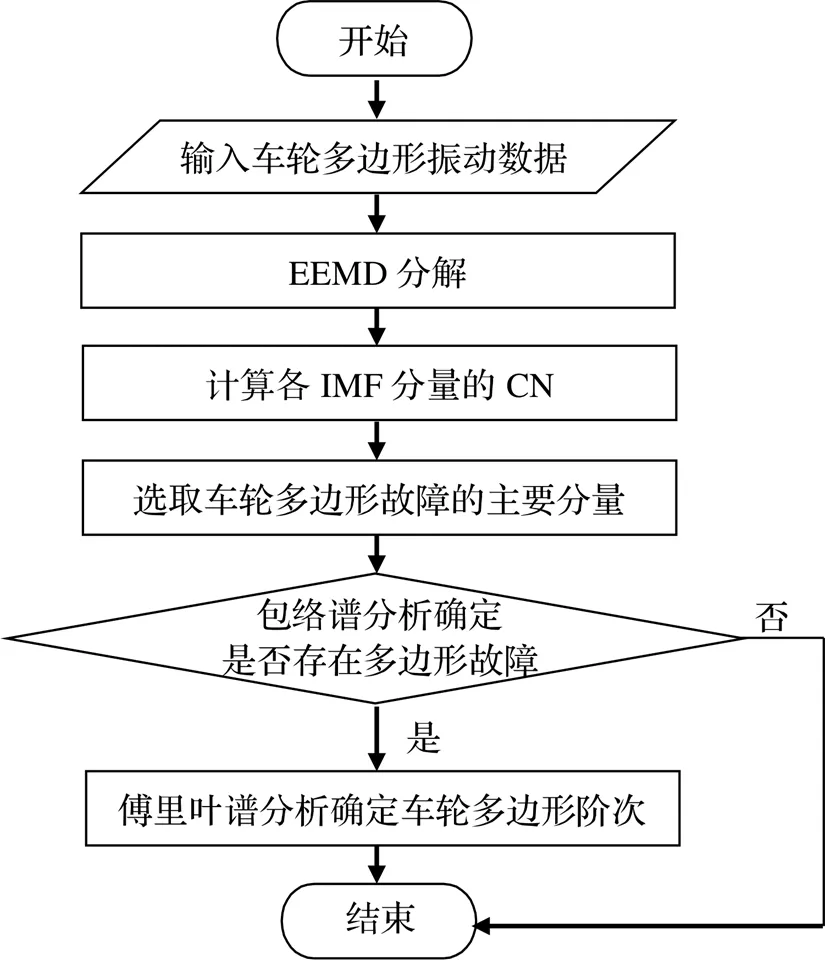
圖1 車輪多邊形故障診斷流程

2 仿真信號驗證

2.1 車輪多邊形故障仿真

為研究出現車輪多邊形時軸箱的振動加速度響應，本文基于多體動力學原理建立了HXD1型機車的SIMPACK模型，然后基于有限元軟件ANSYS的子結構模塊建立HXD1型機車的柔性體模型，并通過SIMPACK軟件的FEMBS接口導入SIMPACK模型中，得到HXD1型機車的剛柔耦合模型，如圖2所示。

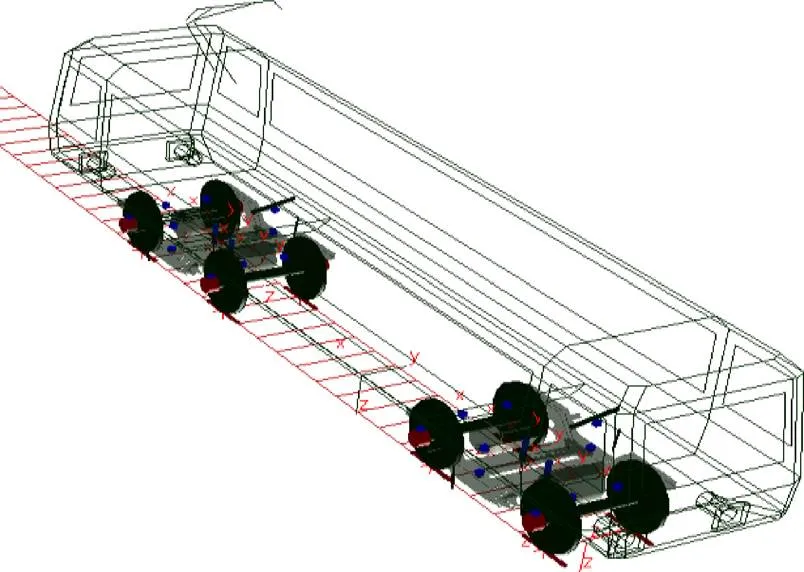
圖2 HXD1型機車車輛模型

模型由1個車體、2個構架、4個輪對、8個軸箱以及一系懸掛和二系懸掛等組成，為了提高計算效率，其中1個輪對為柔性體模型，其余3個輪對為剛體模型。

傳統模型只分析周期性多邊形故障[16]，本文還分析了早期車輪多邊形常見的非周期性多邊形故障。實際工程應用中，均以車輪圓周向半徑的粗糙度描述車輪不圓的程度[6,17]，本文通過式（8）將車輪周向半徑粗糙度轉化為各階不圓對應的磨耗深度。

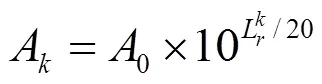
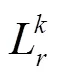
通過式（8）得到各階車輪多邊形對應的磨耗深度，并將其與車輪半徑相加，即可得到非周期性多邊形車輪半徑的周向描述文件。將該周向描述文件導入SIMPACK中，即可實現非周期性車輪多邊形故障仿真。模型中，多邊形主導階次為17階、最大徑跳值約0.2 mm、列車運行速度80 km/h、車輪直徑1250 mm、軌道激勵為美國5級譜、采樣頻率2000 Hz，采樣時間4 s，得到軸箱振動加速度信號及其頻譜如圖3、圖4所示。

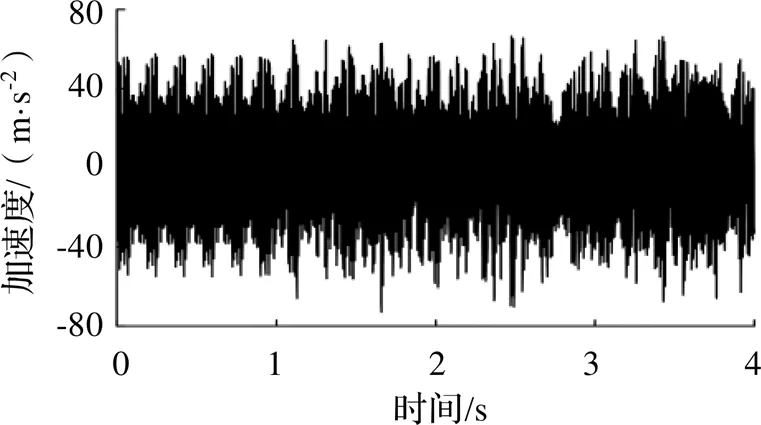
圖3 車輪多邊形故障仿真信號

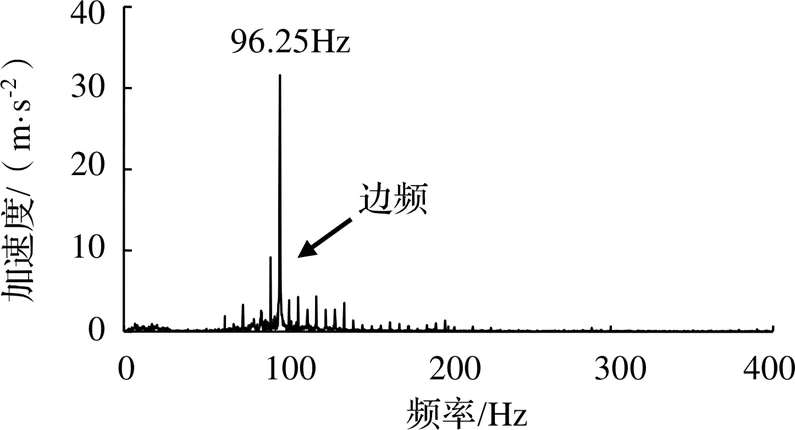
圖4 車輪多邊形故障仿真信號頻譜

仿真信號幅值約為-60～60 m/s2，其頻譜最高幅值對應頻率為96.25 Hz，速度80 km/h對應車輪轉頻為5.66 r/s，計算得到車輪多邊形階次為17.01。在頻率最高值附近，還存在以車輪轉頻為間隔的邊頻帶，這是由于非周期性多邊形是由多個不同階次多邊形疊加而成，并且軸箱振動信號受車輪轉頻調制。

2.2 基于仿真信號的算法驗證

對圖3所示車輪多邊形故障仿真信號進行EEMD分解，得到不同頻率特征的IMF分量，頻率由高到低排列的IMF分量及其頻譜分別如圖5、圖6所示。可知，IMF1中主要是包含了與車輪多邊形無關的白噪聲；IMF2是多邊形信號分量，其頻譜最高幅值對應頻譜為96.25 Hz，最高頻譜附近有車輪轉頻為間隔的邊頻帶，且頻譜幅值大于原信號頻譜幅值，因此該分量比

原信號信噪比高；IMF3～IMF6頻譜幅值較低，且無車輪多邊形故障特征，因此是與車輪多邊形故障無關的低頻分量；IMF7～IMF10是低頻趨勢項或一些虛假分量。

為自適應識別車輪多邊形故障相關的IMF分量，分別計算各IMF分量的相關能量值，結果如表1所示。表1中IMF2的相關能量值最大，而白噪聲分量IMF1以及其他與多邊形故障無關的分量IMF3～IMF10的相關能量也遠小于IMF2的相關能量，由此相關能量可有效篩選出與車輪多邊形故障相關的IMF分量。

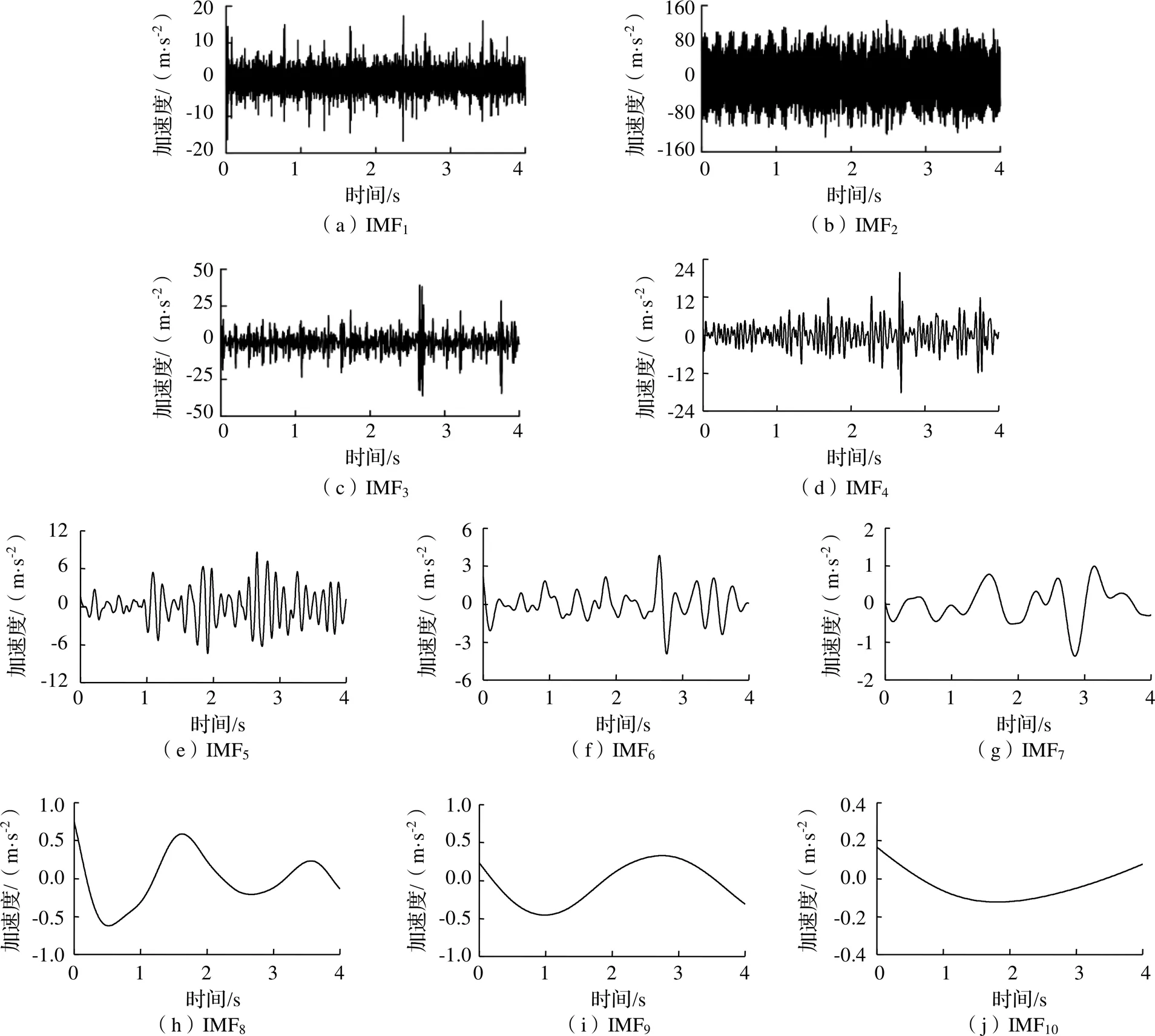
圖5 仿真信號IMF分量

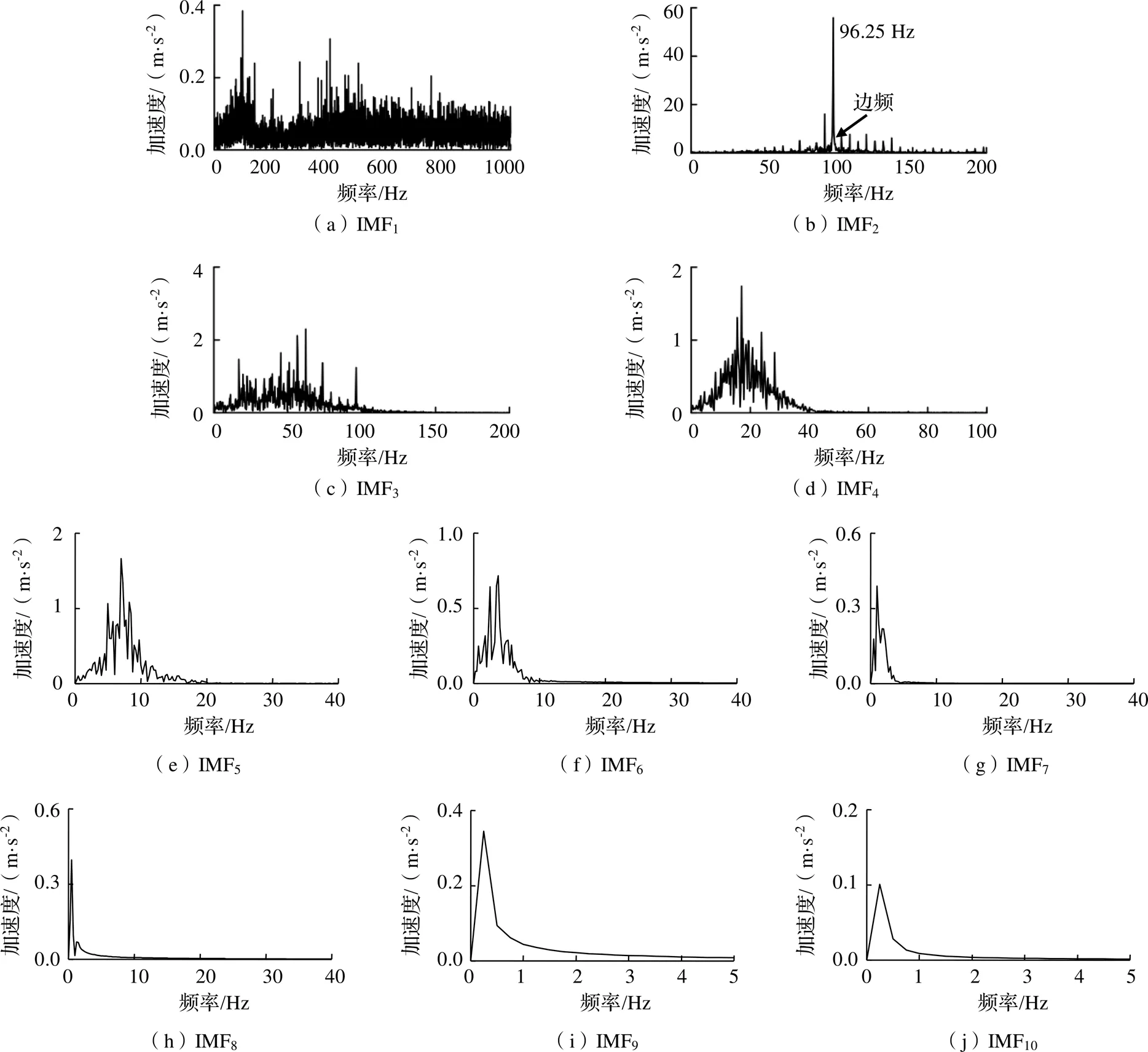
圖6 仿真信號IMF分量頻譜

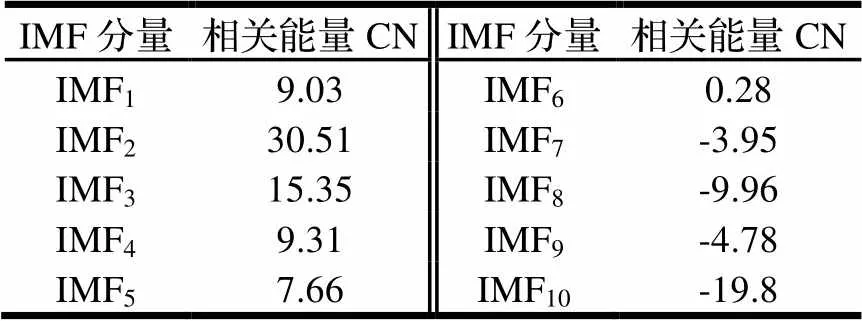
表1 仿真信號IMF相關能量

車輪多邊形故障的主要分量為IMF2，計算IMF2的包絡譜，結果如圖7所示，其中可以清楚看到車輪轉頻及其倍頻，因此可以診斷出車輪踏面存在故障，由圖6可知，IMF2頻譜最高幅值對應頻率為96.25 Hz，由此診斷出車輪多邊形階次為17.01。

根據以上分析，對原信號進行EEMD分解后計算相關能量值，通過最大相關能量可以選出與車輪多邊形信號相關的IMF分量，對該分量做包絡譜分析即可診斷出該車輪是否存在多邊形，并可以根據傅里葉頻譜確定車輪多邊形故障階次，從而驗證了該方法的有效性。

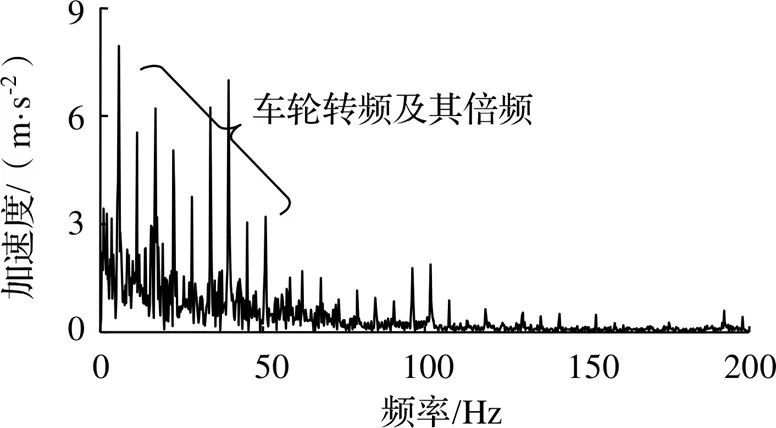
圖7 仿真信號IMF2包絡譜

3 線路實測信號驗證

3.1 車輪多邊形線路試驗

線路試驗車型為HXD1型機車，列車最大運營速度為80 km/h，車輪名義滾動圓直徑為1250 mm。通過在輪對軸箱位置加裝加速度振動傳感器，采集車輪多邊形故障軸箱振動加速度響應，傳感器安裝位置如圖8、圖9所示。傳感器選用運達科技YZ-JXH型振動溫度復合傳感器（量程為±100）；采集系統為運達科技YZD-2數據采集系統，可同時采集軸箱測點振動加速度信號和列車運行速度。

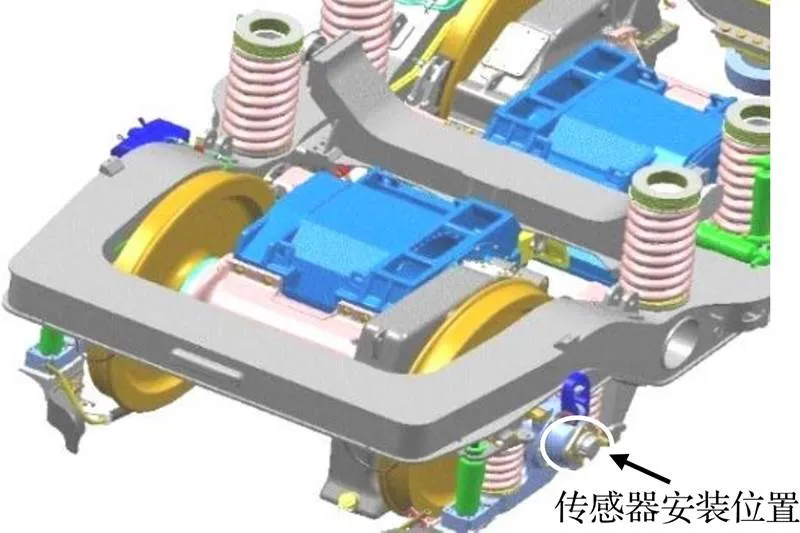
圖8 傳感器安裝位置示意圖

圖9 傳感器現場安裝圖

在列車以60 km/h勻速運行時，采集軸箱振動加速度，采樣頻率2000 Hz，采樣時長4 s，數據總長度8000，其時域信號和頻譜如圖10、圖11所示。可以看到，時域信號幅值約為-20～20 m/s2，98 Hz附近存在車輪轉頻為間隔的邊頻帶，但在低頻段還有軌道或其他部件振動產生的低頻振動信號，這些信號都會對車輪多邊形診斷造成一定干擾。

3.2 線路實測信號驗證

對圖10所示多邊形加速度信號進行EEMD分解，得到頻率由高到低的一系列IMF分量，并計算相關能量CN，結果如圖12、表2所示。

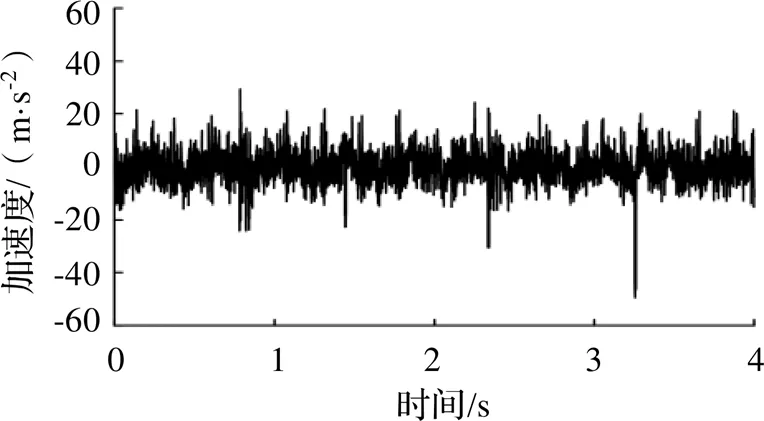
圖10 車輪多邊形線路實測數據

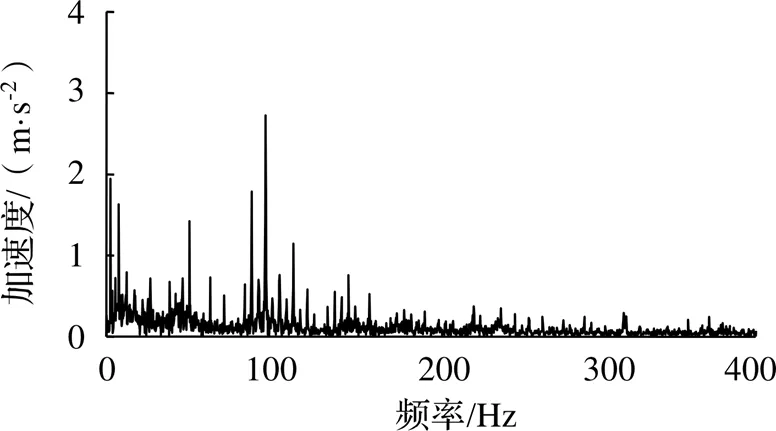
圖11 車輪多邊形線路實測信號傅里葉頻譜

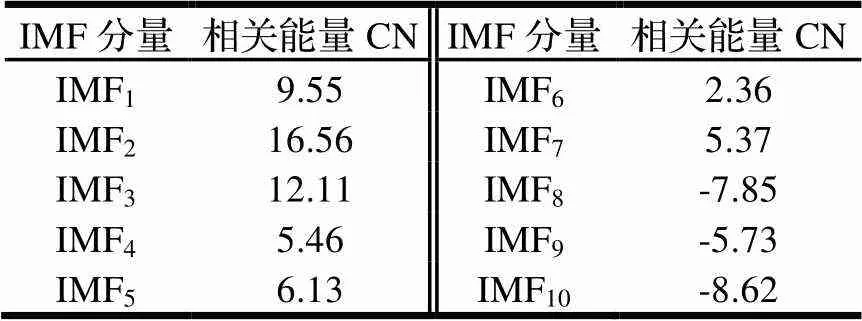
表2 線路實測數據IMF相關能量

表2中IMF2相關能量最大，計算IMF2的包絡譜，結果如圖13所示，可以清晰看到車輪轉頻及其倍頻，因此可以診斷出車輪多邊形故障。計算IMF2的傅里葉頻譜，結果如圖14所示，頻譜最高幅值對應頻率為98 Hz，且最高幅值附近存在車輪轉頻為間隔的邊頻，當車速為60 km/h時，車輪轉頻為4.25 r/s，因此車輪多邊形階次為23階。相比圖11，圖14中IMF2的頻譜在低頻段干擾更少、信噪比更高，更有利于診斷車輪多邊形故障。

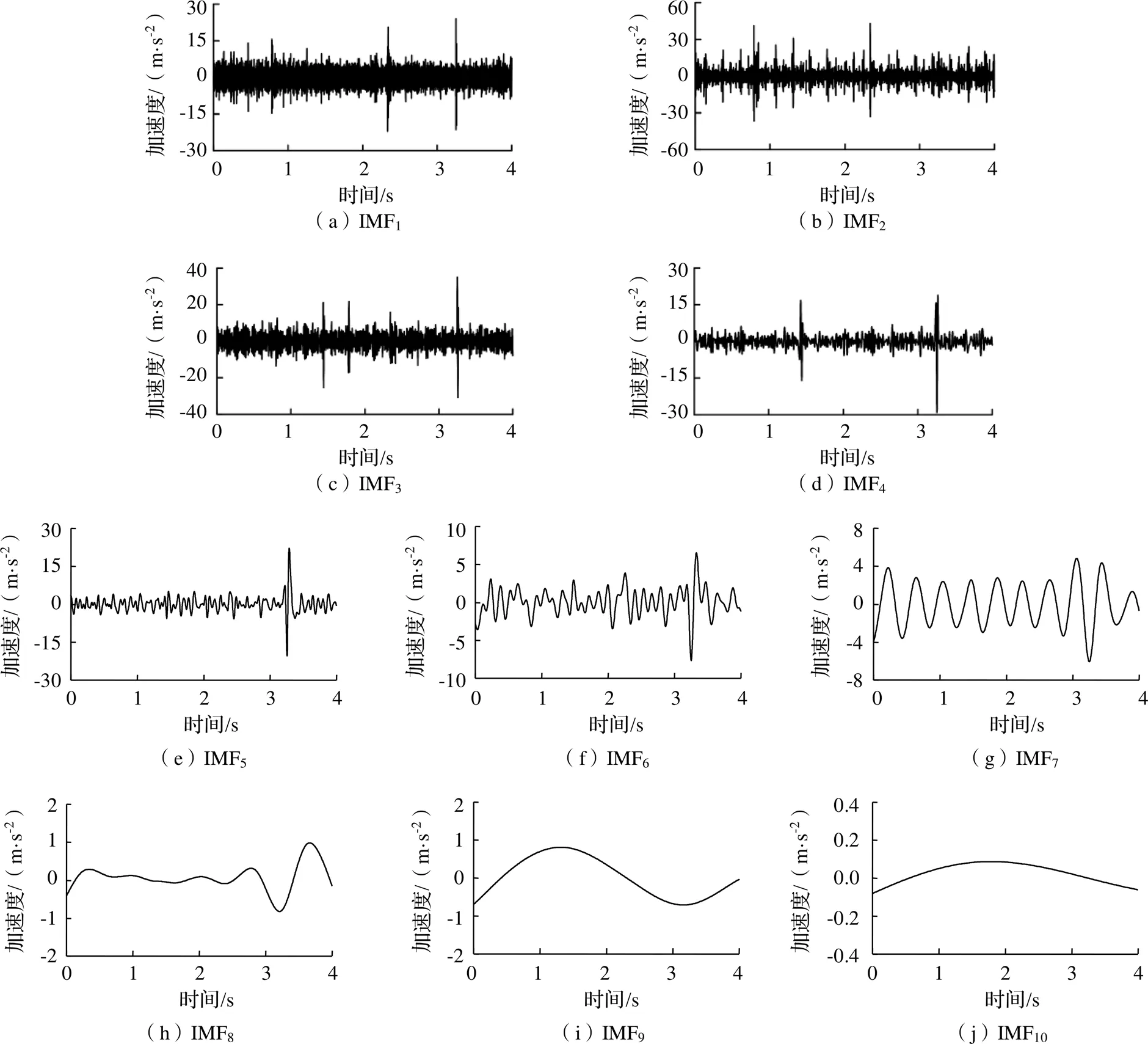
圖12 線路實測數據IMF分量

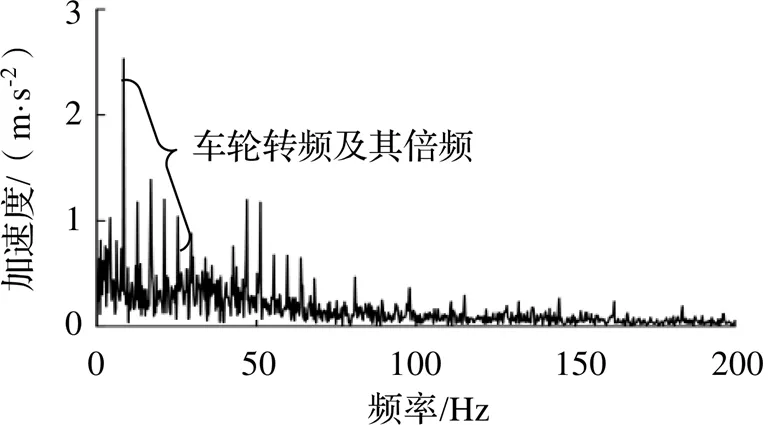
圖13 實測信號IMF2包絡譜

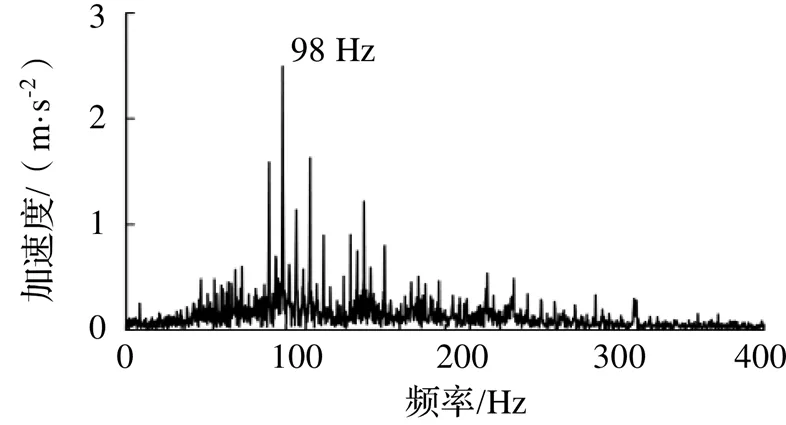
圖14 實測信號IMF2傅里葉頻譜

4 結論

（1）提出相關能量指標，并將其作為車輪多邊形故障指標，該指標能抑制白噪聲和其他周期性成分的干擾，能很好地表征原信號中是否存在多邊形故障成分；

（2）提出基于EEMD分解的車輪多邊形故障診斷方法，并提出利用相關能量CN自動識別車輪多邊形故障對應的IMF分量，得到信噪比更高的車輪多邊形振動信號，最后通過仿真信號和試驗信號驗證了該方法的有效性。

[1]何偉，張合吉，陳帥，等. 車輪多邊形對地鐵車輛一系鋼彈簧疲勞壽命的影響研究[J]. 機械，2020，47（6）：44-50.

[2]張國平，張志波，吳興文，等. 多邊形激勵下動車組動態響應研究[J]. 機械，2020，47（5）：67-74.

[3]江英杰，李偉，陶功權，等. 車輪多邊形磨損對高速線路軌道動態行為影響的試驗研究[J]. 噪聲與振動控制，2019，39（6）：117-121，245.

[4]Cai W，Chi M，Wu X，et al. Experimental and numerical analysis of the polygonal wear of high-speed trains[J]. Wear，2019（440-441）：203079.

[5]Fu B，Bruni S，Luo S. Study on wheel polygonization of a metro vehicle based on polygonal wear simulation[J]. Wear，2019（438-439）：203071.

[6]陶功權. 和諧型電力機車車輪多邊形磨耗形成機理研究[D]. 成都：西南交通大學，2018.

[7]王曉龍. 基于改進的Wigner-Ville時頻分析的城軌列車車輪不圓檢測方法研究[D]. 南京：南京理工大學，2017.

[8]謝利明，高曉蓉，羅林，等. 車輪踏面不圓度在線監測技術的現狀與分析[J]. 鐵道技術監督，2012，40（6）：12-14.

[9]劉志亮，潘登，左明健，等. 軌道車輛故障診斷研究進展[J]. 機械工程學報，2016，52（14）：134-146.

[10]李奕璠，劉建新，李忠繼. 基于Hilbert-Huang變換的列車車輪失圓故障診斷[J]. 振動.測試與診斷，2016，36（4）：734-739，812-813.

[11]徐曉迪，劉金朝，孫善超，等. 基于車輛動態響應的車輪多邊形自動識別方法[J]. 鐵道建筑，2019，59（9）：101-105.

[12]孫琦，張兵，李艷萍，等. 一種波長固定的車輪多邊形在線故障檢測方法[J]. 鐵道科學與工程學報，2018，15（9）：2343-2348.

[13]Zhaohua Wu，Norden E. Huang. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis，2009，1（1）：1-41.

[14]Huang N E. Review of empirical mode decomposition[J]. Proceedings of Spie-wavelet Applications VIII，2001（4391）：71-80.

[15]陳東月. 基于改進的CEEMD及IMF價值評價的高速列車齒輪箱故障診斷研究[D]. 成都：西南交通大學，2018.

[16]王憶佳. 車輪踏面傷損對高速列車動力學行為的影響[D]. 成都：西南交通大學，2014.

[17]陳龍. 地鐵車輪不圓形成機理研究[D]. 成都：西南交通大學，2019.

[18]陳博，陳光雄. 基于MEEMD和GA-SVM的列車車輪多邊形故障識別方法[J]. 噪聲與振動控制，2018，38（03）：157-161+197.

The Method of Wheel Polygonal Fault Diagnosis Based on EEMD

LI Fenglin，DU Hongmei，WU Zhongshu，CHEN Xiangyu，FAN Yiwei

( Chengdu Yunda Technology Co., Ltd., Chengdu 611731, China )

As one of the common failure forms of train wheels, polygonal fault not only increase the vibration and noise of the railway vehicle, reduce the ride comfort of the railway vehicle, but also enhance the force between the wheel and the rail, which leads to premature fatigue and failure of the vehicle and track components, thus affect the safe and stable operation of railway vehicles. Therefore, it is of great significance to diagnose the polygonal fault of the wheel. According to the vibration response of the axle box of the polygonal wheel, a fault diagnosis method of polygonal wheel based on EEMD is proposed in this paper. The core of the proposed method is to perform EEMD decomposition of the axle box vibration acceleration, and then automatically extract the IMF component of the polygonal fault through the correlated energy (CN), and next diagnose the wheel polygonal fault through the envelope spectrum analysis, and finally determine the polygon order through the spectrum analysis. Simulation test and line test are conducted to verify the effectiveness of the proposed method, which proves that the proposed method can effectively diagnose the wheel polygonal fault effectively.

wheel polygon；EEMD；correlated energy；fault detection

U279.3+23

A

10.3969/j.issn.1006-0316.2021.05.007

1006-0316 (2021) 05-0043-09

2020-10-19

李鳳林（1992－），男，四川資陽人，碩士，工程師，主要研究方向為旋轉件故障診斷，E-mail：13320686432@163.com。