基于蟻群聚類的不平衡數據過采樣方法
高 陽,劉其成,牟春曉
(煙臺大學計算機與控制工程學院,山東 煙臺 264005)
不平衡數據集是指樣本集中各自類別所含樣本數目的多少存在較大的差距,對于含有較多樣本數的類別稱之為多數類(反例)樣本,反之為少數類(正例)樣本[1]。在不平衡數據集中,樣本數量較少的類可能包含更加關鍵的信息。例如醫療診斷中人類患腫瘤性疾病的事件屬于少數類,但是如果將腫瘤性疾病誤診為沒有病變,可能就會喪失早期治療的機會,造成難以挽回的結果[2]。不平衡分類產生的原因是采用普通分類方法去處理不平衡數據集導致分類器的分類結果不理想[3]。例如一個數據集中有998個反例,2個正例,那么只需要選擇一個將訓練集數據預測為反例的學習方法即可,這樣該學習方法生成的學習器就可以達到99.8%的分類精度。但這樣的學習器對不平衡數據集的研究起不到任何積極的作用,因為它往往是預測不出正例的。隨著大數據時代的到來,現在這種問題普遍存在于故障檢測、信用卡欺詐檢測、網絡入侵識別以及電子郵件分類等領域,因此如何將不均衡的數據集既快速又準確的處理是當下學術研究的一個熱門方向[4-7]。
通常從算法和數據2個層面解決不平衡數據集問題[8]。數據層面有2種選擇,分別是增大正例樣本數目的過采樣以及縮減反例樣本數目的欠采樣。二者有一定的共同之處,都是通過改變各自類別的樣本數目使數據集達到一定程度的平衡。代表性的算法有合成少數類過采樣技術SMOTE[9]。算法層面所用到的方法,主要是在得到平衡數據集之后,通過引入代價矩陣或者對分類錯誤率進行改進。將數據層面的方法和算法層面的方法結合起來得到的新分類器可以具有更強的多元性和魯棒性。
傳統分類器將不平衡數據集中的少數類預測正確的精度很低,為此對于上文提到的2種解決方案,當前研究者大都以增加數據集中的正例樣本數目為切入點。文獻[9]所用的SMOTE算法是針對所有的正例樣本過采樣,容易產生重疊的新合成的正例樣本。Safe-level SMOTE[10]算法會對每個少數類樣本的檢測其臨近同類樣本的個數,并以此設置每個少數類樣本的安全等級,當其值高于一定閾值時才會對此樣本進行過采樣。該方法在一定程度上避免了噪聲數據的產生,但合成數據都過于集中在少數類內部可能會出現過擬合現象。DB-SMOTE算法[11]以正例子簇簇心的距離為標準進行過采樣,挑選那些邊際處的正例樣本當作種子,以此避免過擬合現象,但這種方法容易產生重疊樣例。WOHC算法[12]考慮到在過采樣時會產生重疊樣本以及導致過擬合問題,采用加權過采樣的方法避免產生重疊樣本,但是該方法只能起到預防的作用,并不能起到根除產生重疊樣本的作用。
對于上述問題,本文提出基于蟻群聚類改進的SMOTE不平衡數據過采樣算法ACC-SMOTE(Ant Colony Clustering Synthetic Minority Oversampling Technique)。首先采用改善的蟻群聚類算法將正例樣本劃分為不同的子簇,而后再根據各個正例子簇所占的樣本比例采用SMOTE算法來過采樣;最后讓經過上述操作的正例樣本采用Tomek Links方法及時改正,清理掉正例樣本集中產生的噪聲數據,進而提高合成之后正例樣本的質量。本文提出的ACC-SMOTE算法與經典的SMOTE[9]、Safe-leve SMOTE[10]、DB-SMOTE[11]、WOHC[12]算法相對比,實驗結果顯示該方法使正例樣本的預測精準度得到提升。
1 預備理論
1.1 SMOTE算法
CHAWLA等[9]在2002年提出了對正例樣本合成的方法,即SMOTE。首先隨機選擇一個正例樣本,然后再找出距離它最近的k個樣本,按照采樣概率從距離它最近的k個樣本中選擇一個樣本按照公式(1)合成新樣本,反復執行以上過程使數據集達到平衡。
Y=X1+rand·(X1-X2)。
(1)
其中,X1正例樣本,X2是距離X1最近的k個樣本中的一個,rand是隨機生成一個從0至1區間內的數的函數,Y代表了新生成的正例樣本。
1.2 蟻群算法基本原理
蟻群聚類算法的思想是讓螞蟻在一個含有許多數據的區域隨機挪動轉移[13]。當螞蟻隨機挪動到其中一個帶有數據的區域時,計算該數據在它領域內的相似度來得到螞蟻背負它的概率,如果該概率比隨機數大,螞蟻撿起該數據并背負它隨機挪動轉移,否則螞蟻不撿起該數據繼續隨機挪動轉移;在螞蟻背負數據隨機挪動轉移到不含數據的空白區域時,計算空白區域的相似度得到丟棄該數據的概率,若概率值大于隨機數則丟棄,反之丟棄失敗,繼續挪動轉移到別的空白區域判斷。蟻群經過上述過程反復的撿起、挪動轉移、丟棄當達到某個循環結束標志時就會得到一個最終的聚類結果。
1.3 Tomek Link數據清理技術
Tomek Links是對數據集清理的一種關鍵技術,可以用它來清理那些因過采樣而產生的噪聲數據和重疊樣例[14]。其主要思想是將Tomek Links看作是1對數據實例,它們距離(歐式距離)很近但屬于不同的類別。只有當2個數據實例中的1個是噪聲數據或者2個數據實例都在各自類別的邊界上時,這2個數據實例才有可能構成一對Tomek Links。比如給定1對數據(xi,xj),xi,xj屬于不同的類別,即少數類xi,多數類xj,用d(xi,xj)表示它們之間的歐式距離。如果不存在另一數據實例x,使得d(xi,x) 為了獲取更多數據集中正例樣本所表示的信息內容,本文通過致力于改進SMOTE過采樣算法得到ACC-SMOTE算法,使各自類別的樣本數目達到相對均衡。該算法不僅著眼于數據集不同類別之間的不平衡,還想到同類之間不同子簇所含樣本數目的差異以及噪聲數據對樣本的影響。采用蟻群聚類得到最優解,為下一階段采用SMOTE算法過采樣合成樣本提供更準確的聚類結果,從而得到更理想的合成樣本。為了根除合成新樣本產生的重疊樣本,該算法采用了Tomek Links方法。ACC-SMOTE算法主要分為三部分:蟻群聚類階段,過采樣階段,合成數據整理階段。 在ACC-SMOTE算法的初始階段,需要將訓練集先進行預處理操作,即將訓練集中的少數類進行聚類,分為不同的子簇,然后再根據其所占的比例進行過采樣。這樣做的目的是著眼于數據集不同類別之間的不平衡而且還有同類之間不同子簇所含樣本數目的差異,從而保證合成樣本的質量,防止過擬合。 為避免一個數據反復地被拾起放下,導致聚類速度變慢,同時也為了避免因為隨機性導致聚類結果的準確性降低,ACC-SMOTE算法采用的蟻群聚類方法每只螞蟻對應一種聚類方案,轉移方程中只有信息素權重。這是因為每個簇的聚類中心需要不斷地移動,轉移期望不好衡量,所以轉移方程中沒有轉移期望。在搜索解空間選擇某個點的類別時,將信息素看成當前點與每個類別的臨近程度,以概率p挑選信息素最高的點,1-p的概率按信息素分布用輪盤賭方法挑選。概率p計算公式如下: (2) 式(2)中1-pTh的值表示螞蟻在搜索路徑中隨機因素作用的強度,其值越大,選擇走過路徑的概率越大,從而導致局部最優,因此將直接轉移閾值設為pTh=0.9;τij(t)表達的意思是時間為t時,邊(i,j)上所含的信息素。 更新信息素方面,為了解決其更新缺乏時效性的問題,根據方案的優度(1/MSE)來增加方案上所有點-類對的信息素,每次迭代,每只螞蟻都得到一個方案;然后刷新每個點-類對上的信息素的濃度值。具體公式如下,其中所有方案已按MSE升序排好。 τij(t+m)=(1-volR)·τij(t)+Δτij(t), (3) (4) (5) 式(3)中考慮到信息正反饋的作用,volR較小時,信息正反饋占主導地位,算法收斂速度加快。為了提高蟻群聚類算法的收斂速度,可將信息素的散發率適當降低為volR=0.1,式(4)中刷新信息素的最優方案數updNum=3,式(5)中信息素系數pherC=107,最優方案MSE的數組為sol數組。 上述算法的偽代碼如下: 輸入:聚類數K,樣本數N,少數類mindata 輸出:K個少數類子簇 (1)每只螞蟻對應一種解決方案。 (2)初始化,生成一個較好的聚類方案,讓所有螞蟻都從該方案出發。 (3)將信息素看成當前點與每個類別的臨近程度,根據公式(2)搜索解空間。 (4)依靠公式(3)(4)(5)刷新信息素;依靠方案的優度來增加方案中所有點類對的信息素。 (5)反復執行步驟(2)(3)(4),直到Num大于MaxNum或方案連續CRN次重復并且Num大于MinNum,結束循環(Num表示目前執行了循環多少次,MaxNum和MinNum分別代表最多和最少可以執行循環多少次)。 對于步驟(1)(2)使用最近距離輪盤賭法,在給定的N個正例樣本中選擇較分散的K個數據樣本當成初始的子簇中心,按最近距離給出初始的聚類方案,存到每只的solution數組中;然后讓所有螞蟻都從該聚類方案出發。步驟(4)的更新過程中,將會失去volR比例的信息素,MSE較小的updNum個方案對其點-類對的信息素產生增量。 經過上述改進的蟻群聚類可以得到不同少數類的子簇,其中2.1節的4個公式是該算法的核心,直接決定了聚類結果的好壞。采用SMOTE算法對少數類進行過采樣大致可分為以下2個部分,首先將少數類劃分為不同的子簇,根據每個子簇大小所占樣本的比例確定采樣比重T,如公式(6)。然后按照公式(1)對不同子簇的少數類進行過采樣,重復執行以上過程直到達到過采樣比重。SMOTE算法可以使正例樣本數目增加,進而改善數據集的不平衡性。 Ti=(Nmax-Nmin)×(Nmin-Ci)/Nmin。 (6) 式(6)中Nmax,Nmin分別代表反例以及正例的樣本數目;Ci表示當前子簇的樣本數目;Ti代表i子簇的采樣比重。 單個正例樣本簇實現SMOTE過采樣的偽代碼如下。 輸入:正例樣本簇mindata,反例樣本數m1,正例樣本數m2 輸出:合成樣本后新的正例樣本簇new-mindata (1)[r1,c1]=size(mindata); (2)//確定采樣比例 (3)T=(m2-m1)×(m1-r1)/m1;//計算過采樣之后的簇樣本數 (4)ratio=T./r1;//使用每個樣本的KNN次數 (5)k=5;//近鄰數 (6)new-mindata=mySMOTE(mindata,ratio,k); (7)//調用另個函數中SMOTE算法根據公式(1)過采樣 (8)[r2,c2]=size(new-mindata); (9)ifr2>T (10)new=randperm(r2,T); (11)new-mindata=new-mindata(new,:); (12)else (13)new=randperm(r2,T-r2); (15)end if 樣本合成示例如圖1。 圖1 過采樣合成樣本示例 普通情況下在合成新的少數類樣本時產生噪聲樣本是不可消除的,而且噪聲樣本的存在會使分類器的性能下降。況且對少數類來說,樣本數目少就導致了它本身抗噪聲能力弱的缺陷,從而噪聲數據對分類效果產生較大的影響。通過過采樣對少數類樣本合成,從而使得樣本集中各類樣本數相對平衡。如果在過采樣時種子樣本的近鄰樣本是多數類樣本,那么合成之后的樣本就會是噪聲數據,在使用分類器進行分類時就不會提供有用的信息,反而可能會誤導分類器做出錯誤的判斷,進而會降低其分類精度。因此ACC-SMOTE算法采用Tomek Links數據清理技術處理新合成的樣本,其思想已在1.3節有簡單介紹,下面主要給出Tomek Links算法實現的偽代碼。 輸入:原始數據集Originaldata,數據的維度ic 輸出:Cleardata (1)min-dist=zeros(size(Originaldata,1), 1); (2)tomek-link=[]; 5)回噴入爐工藝。發達國家垃圾熱值高,含水率低,且實行垃圾分類收集處理的方式,所以發達國家垃圾滲瀝液產生量小,可直接回噴入爐燃燒,解決了滲瀝液濃液的二次污染問題[1]。但我國生活垃圾沒有分選,生活垃圾中廚余垃圾占比大,含水率高,滲瀝液及處理后的濃縮液產生量大[2]。若全部回噴入爐,將降低爐溫,造成燃燒負荷波動大,甚至850℃、2 s無法保證,且減少鍋爐的蒸發量和整個電廠發電量[3-4]。 (3)fori=1: size(Originaldata, 1) (4)sample-mat=repmat(Originaldata(i,1:ic-1), (5)size((Originaldata,1), 1); (6)dists=sum(abs(Originaldata(:,1:ic-1)-sample-mat), 2); (7)[ds,id]=sort(dists); (8)if Originaldata(id(2),ic)~=Originaldata(i,ic) (9)min-dist(i)=id(2); (10)if min-dist(id(2))==i (11)if Originaldata(i,ic)==0 (12)tomek-link=[tomek-linki]; (13)else (14)tomek-link=[tomek-linkid(2)]; (15) end if (16) end if (17) end if (18) end for (19)Originaldata(tomek-link,:)=[]; (20)Cleardata=Originaldata; (21)Output Cleardata 實驗過程將分別對多組UCI數據集采取二八分原則將數據集分為測試集以及訓練集[15],用上述方法來驗證算法的有效性以及可行性。由于實驗中數據集的劃分以及合成新樣本時存在偶然性,因此下面的結果都是執行多次取得的平均值。 對于不平衡數據集,傳統的分類結果精準度和評價指標已不適用,為此采用從如表1所示的混淆矩陣中得到新評價指標G-means[16]和F-value[17]。 表1 混淆矩陣 根據表1可以得到如下所示的評價指標: 正類樣本召回率: (7) 負類樣本召回率: (8) 正類樣本查準率: (9) G-means值: (10) F-value值: (11) G-means值綜合考量正例樣本和反例樣本的召回率,只有當兩者值都大時,G-means值才會大,可以更精確地顯示出模型的分類效果。而F-value值著眼于對正例樣本的查準率和召回率,可以更加精確地顯示出正例樣本的分類準確度。由此本文實驗將由G-means值和F-value值作為評價模型的指標。 在實驗之前,對一些數據進行整合,主要包括刪除有屬性缺失的數據和將多分類轉變成二分類。數據集結構如表2。 表2 UCI數據集 為了證明ACC-SMOTE算法的有效性及可行性,在Blood、Breast cancer、Ecoli、Haberman、Ionoshpere、Pima、Yeast 7種不同的數據集里將SMOTE[9]、Safe-level SMOTE[10]、DB-SMOTE[11]、WOHC[12]4種算法分別結合C4.5分類算法作比較,采用G-means和F-value作為評價指標。把不結合任何過采樣算法的C4.5的分類結果作為比較準則,從實驗結果說明了處理不平衡數據的重要性。實驗結果如表3。 從表3中可以得出在數據集Blood,Haberman,Ionoshpere,Pima,Yeast中,ACC-SMOTE算法的G-means值和F-value值均高于其他算法,G-means值在Blood,Breast cancer,Haberman,Ionoshpere 4組數據集上也取得較好效果。該算法相比于WOHC算法G-means和F-value值均有提升,一方面該算法有效克服了噪聲樣本的影響,另一方面,該算法能夠較好的處理具有分類困難樣本的不平衡數據,有效的明確正例樣本的邊界,進而提高了分類的精度。 表3 ACC-SMOTE算法與其他算法的比較 對于不平衡數據集問題,現在已有的方法大都僅僅著眼于數據集不同類別之間的不平衡,沒有考慮到同類之間不同子簇所含樣本數目的差異,經過過采樣之后的訓練集可能會出現邊緣化問題,訓練出的模型更可能出現過擬合現象,從而降低分類精準度。為了克服現有過采樣算法的不足,提出了ACC-SMOTE算法。該算法針對合成新樣本過程存在的問題,引入聚類思想和數據清理技術,有效降低了數據集中類間、類內的不平衡性以及邊緣化問題出現的概率。經驗證ACC-SMOTE算法可以明顯提高少數類樣本的分類準確度,分類性能更優,從而證明了該算法的可行性與有效性。 現實生活中還會出現多分類的情形,以后的工作可以進一步將多分類數據集的采樣方法作為研究內容,以便于將ACC-SMOTE算法應用于更多領域。2 改進的過采樣算法ACC-SMOTE
2.1 蟻群聚類階段
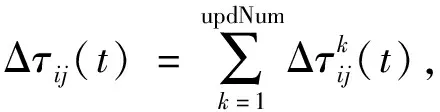
2.2 過采樣階段
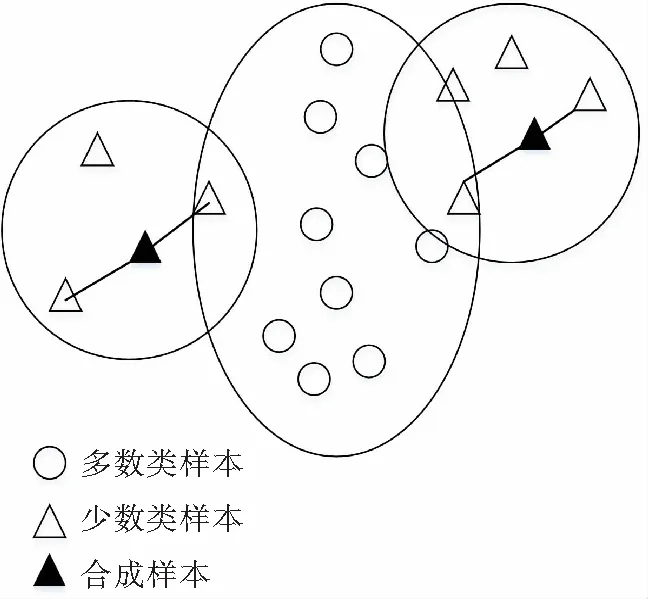
2.3 合成數據整理階段
3 實驗結果分析
3.1 評價指標

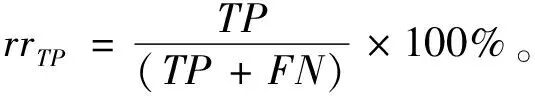
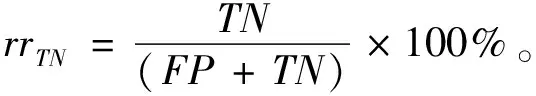
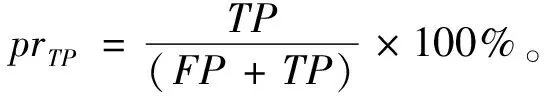
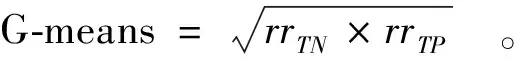
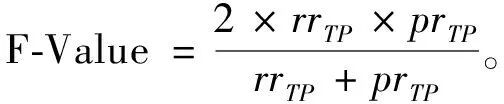
3.2 實驗數據
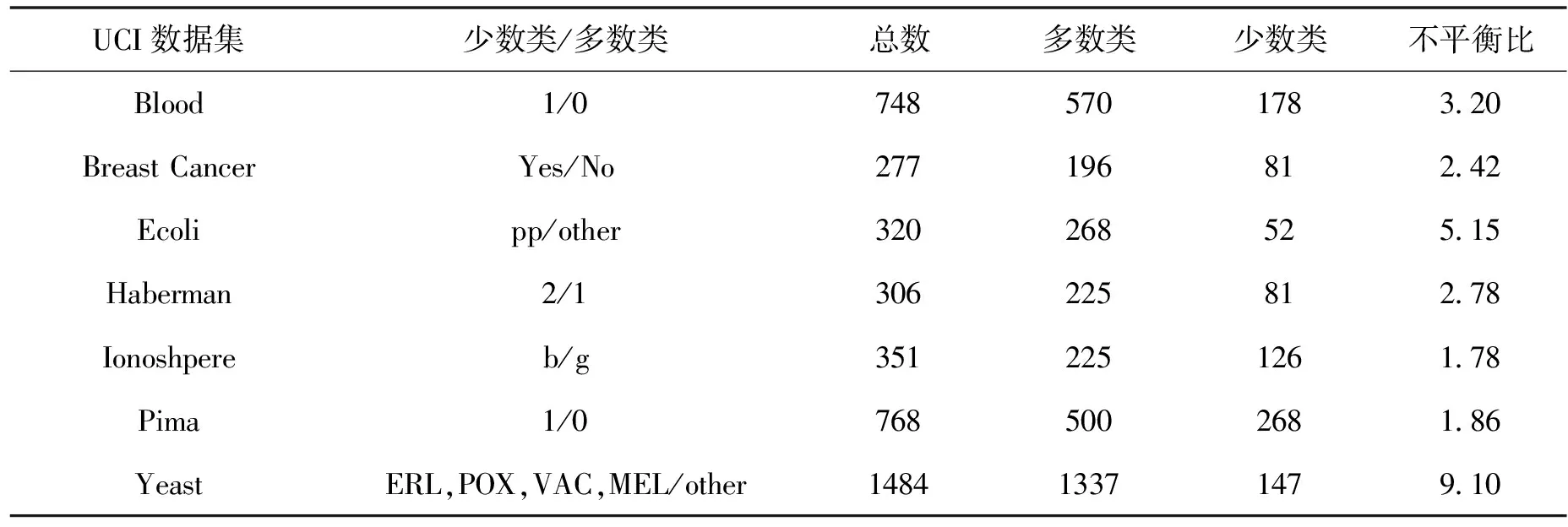
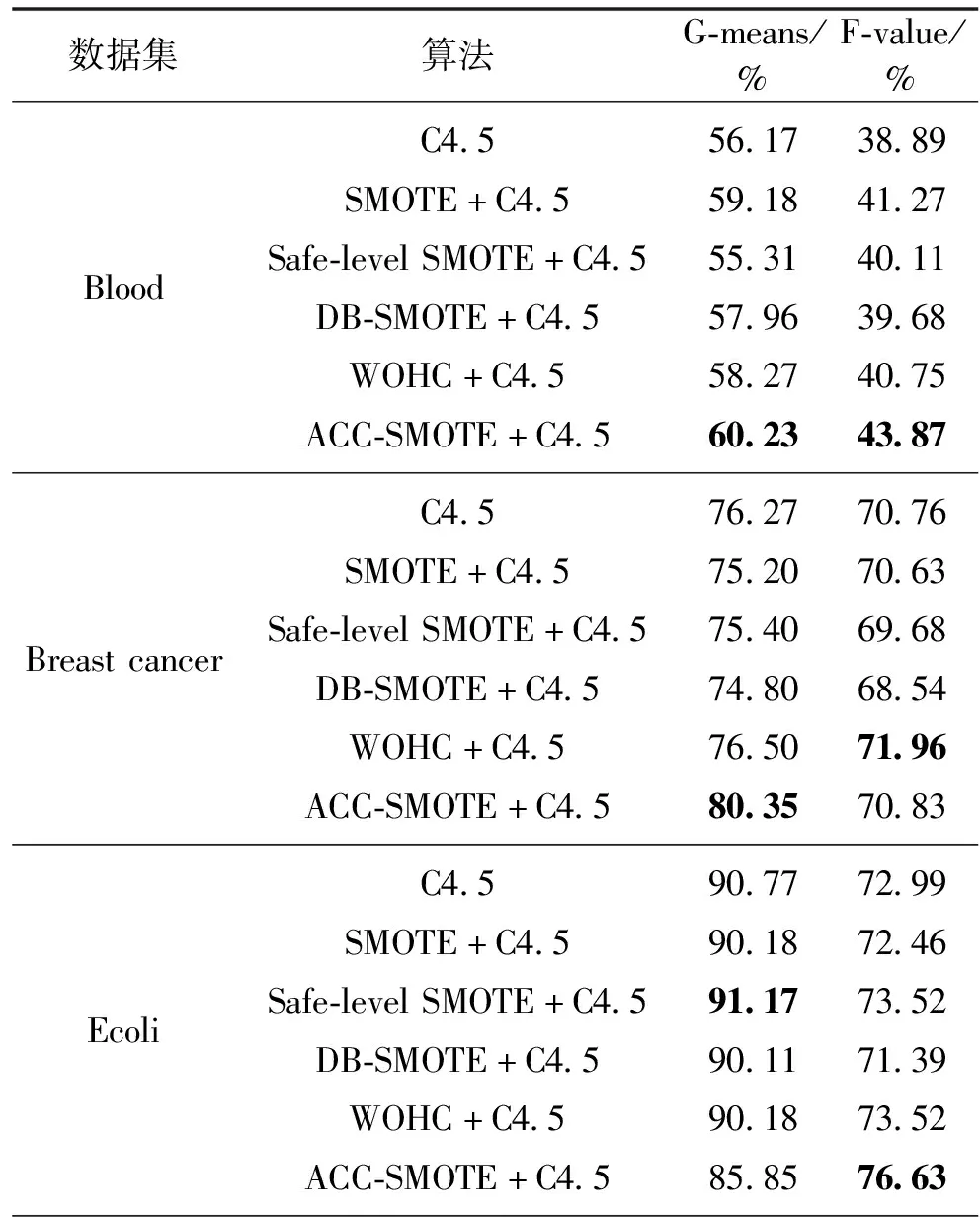
3.3 實驗結果對比
4 結 語

