全長樹脂錨桿在拉拔荷載作用下的軸向力分析

王德全，張 超，張開誠，康明超，郭學庭

(1.山東黃金礦業(萊州)有限公司 三山島金礦，山東 萊州 261442；2.北京科技大學 土木與資源工程學院，北京 100083)

樹脂錨桿已逐漸取代管縫式錨桿成為礦山支護的主導形式[1-5]。考慮樹脂錨桿在拉拔荷載作用下力的分布情況是進行支護的重要前提[6-7]。針對樹脂錨桿的拉拔實驗設計，國內外學者均作出了較多的貢獻，主要研究方法有理論計算、室內實驗、數值模擬三種。

在理論計算研究方面，趙一鳴[8]推導出了與時間有關的桿體拉應力和桿體界面剪應力分布公式，并求解了恒力作用下的樹脂錨桿桿體外端點位移的近似公式；李青峰等[9]基于集中載荷作用于半無限體表面和無限體內部的彈性力學解得到了樹脂錨桿在非錨固段圍巖破碎和完整時的錨固段錨固界面剪應力計算式，分析了錨桿桿體拉力在錨固段錨固界面的剪應力形成機理；尤春安[10]利用Mnidlin問題的位移解導出了全長黏結式錨桿受力的彈性解，討論了錨桿的受力特征及影響因素。

在室內實驗研究方面，肖同強等[11]進行拉拔實驗，將錨桿拉拔荷載—端頭位移發展分為四個階段，得到了不同錨固長度下錨桿拉拔荷載與端頭位移的關系；林健等[12]設計拉拔實驗，對樹脂全長錨固錨桿外形與錨桿錨固性能以及安裝阻力之間的關系進行了研究，提出了錨桿外形相關參數的合理值。趙同彬等[13]基于全長錨固砂漿錨桿的室內拉拔實驗，測試了錨桿桿體與砂漿黏結界面之間的軸向剪應力分布規律。

在數值計算研究方面，崔千里等[14-15]采用FLAC3D對樹脂錨桿錨固段桿體、樹脂藥卷及圍巖之間的作用關系及應力、位移分布規律進行模擬研究，分析了錨固段在不同載荷作用下從彈性狀態到彈塑性狀態的發展變化過程；陳瑤[16]通過在錨桿與樹脂錨固劑之間、樹脂錨固劑與周圍之間設置接觸面單元，研究了錨固界面間的相互作用機理。

上述多種計算方法中，均對樹脂錨桿在拉拔荷載作用下的受力情況進行了相應的分析，并取得了相應的成果。但具體的理論推導過程還有待完善。本文借助Mindlin位移解，詳細推導了樹脂錨桿在拉拔荷載作用下圍巖剪應力和錨桿軸向力的分布變化規律，將其應用于山東黃金某金礦樹脂錨桿的支護設計中，并采用數值模擬對其分布規律進行驗證，為礦山支護設計提供參考依據。

1 圍巖剪應力分布理論計算

1.1 Mindlin位移解

Mindlin[17-19]于1936年基于半無限空間內部受集中力產生各點的變形問題，提出了Mindlin位移解法。如圖1所示，內部作用一豎向集中力F，荷載作用點深度為c，則可得到Mindlin的三維空間位移解式(1)。

圖1 Mindlin解計算簡圖Fig.1 Calculation diagram of Mindlin solution

(1)

式中，E、μ—巖體的彈性模量、泊松比；

1.2 圍巖剪應力分布

本文主要考慮全長錨固情況下圍巖的剪應力和樹脂錨桿的軸向力分布情況。為推導拉拔實驗下圍巖的剪應力分布規律，作如下假設：巖體為線彈性、均勻各向同性的半無限體；樹脂錨桿為線彈性體、無線長度；通過錨桿近端且垂直于錨桿的平面為z=0平面，在該平面錨桿的伸長量與圍巖剪應力產生的位移變形相等。

在原點位置，x=y=z=0，則：

(2)

式中，集中力F(z)=πdτ(z)dz，將其代入式(2)得：

(3)

根據材料力學桿件的拉伸變形，可得錨桿自身的伸長量為：

(4)

在孔口位置(z= 0)，錨桿桿體的伸長量與巖體位移相等，則：

(5)

式中，Ea—樹脂錨桿的彈性模量；Aa—樹脂錨桿的截面積；d—樹脂錨桿的直徑。

對式(5)進行兩次求導，可得：

(6)

(7)

式(7)為一階齊次微分方程，求解其方程為：

(8)

式中，C為常數，當位于孔口位置時，z=0,τ=0；當位于孔底位置時，z=∞,τ=0。結合F(z)=πdτ(z)dz，可得：

(9)

求得，

(10)

于是，求得圍巖的剪應力為：

(11)

(12)

對式(11)中圍巖的剪應力進行積分即可得錨桿的軸向力分布函數，為：

(13)

由式(11)可以看出，圍巖的剪應力、錨桿的軸向力主要與巖體和錨桿的彈性模量比(Ea/E)、錨桿直徑(d)、拉拔荷載(F)有關，增大拉拔荷載(F)、減小錨桿直徑(d)或減小彈性模量比(Ea/E)均會增大圍巖的剪應力。

1.3 工程實例

以山東黃金集團某金礦為背景，考慮樹脂錨桿在拉拔荷載下的軸向力分布情況。該金礦目前已經開采到-308 m水平，圍巖主要為灰巖，礦體主要為角礫巖。作為礦山主要的支護手段，主要采用管縫式錨桿進行支護。但隨著開采深度的增加，管縫式錨桿所起到的支護效果逐漸減弱。因此礦山引進樹脂錨桿，在該水平管縫式錨桿向樹脂錨桿過渡，目前已取得較好的支護效果。

取礦山實際的巖體力學參數，具體如表1所示。樹脂錨桿的直徑為22 mm，其彈性模量為214 GPa，分別取拉拔力為10、20、40、60、80 kN，代入式(11)，可得錨桿在該拉拔荷載作用下圍巖的剪應力關系式，計算結果如式(14)所示。

表1 圍巖的力學參數

(14)

圖2為錨桿在不同拉拔荷載下圍巖的剪應力分布曲線。從圖2可以看出，圍巖剪應力呈負指數分布，在孔口位置圍巖的剪應力值等于零，距離孔口47.48 mm處剪應力急劇增大至峰值，之后不斷減小并在錨固遠端趨于零。圍巖剪應力大小與拉拔荷載的大小成正比，隨著拉拔力的增大，最大剪應力也在不斷增加。

圖2 圍巖剪應力分布曲線Fig.2 Shear stress distribution curves of surrounding rock

對式(14)圍巖剪應力進行積分即可得錨桿的軸向力分布函數，將不同拉拔荷載下錨桿軸向力分布圖繪制成曲線如圖3所示。可以看出樹脂錨桿軸向力分布與圍巖剪應力分布相對應，錨桿軸力大小與拉拔荷載大小成正比，隨著拉拔荷載的增大而增大。在孔口位置樹脂錨桿的軸向力最大，向孔底軸力逐漸減小，最后逐漸趨于零。

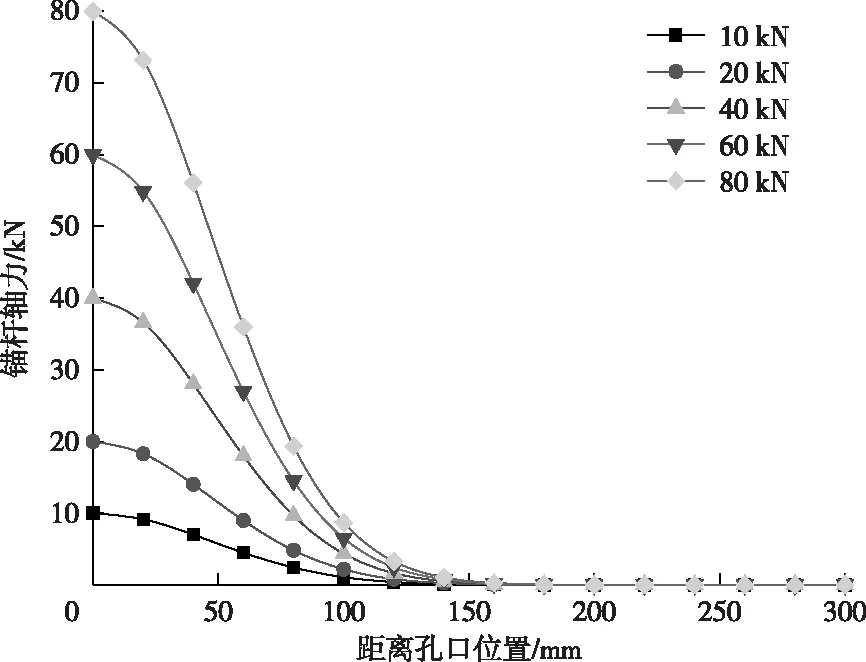
圖3 錨桿軸向力分布曲線Fig.3 Bolt axial force distribution curves

根據圍巖剪應力的分布以及錨桿軸向力的分布可知，孔口近端的錨桿所承受的軸力最大，該處的抗剪強度決定了錨桿的支護所能承受的最大強度。圍巖所承受的剪應力與錨桿軸力相對應，在孔口處圍巖剪應力最大，該處圍巖強度的大小也是錨桿支護強度的一個關鍵因素。因此為提高錨桿的強度可適當增加錨桿桿體近端的抗剪強度，對孔口處圍巖的強度應適當增強。

2 樹脂錨桿拉拔實驗的數值模擬

2.1 模型的建立

為進一步分析樹脂錨桿在拉拔荷載作用下剪應力的分布情況，采用FLAC3D進行樹脂錨桿拉拔實驗模擬。如圖4所示，每個模型的單元都為八節點六面體的實體單元，包括X、Y、Z三個方向的自由度。此次模型計算范圍為2 m×2 m×2 m，共劃分22 400個網格與25 261個節點。巖體、樹脂錨固劑本構模型選用Mohr-Coulomb模型，桿體本構模型選用彈性模型。巖體、樹脂錨固劑、錨桿的主要力學參數如表2所示。

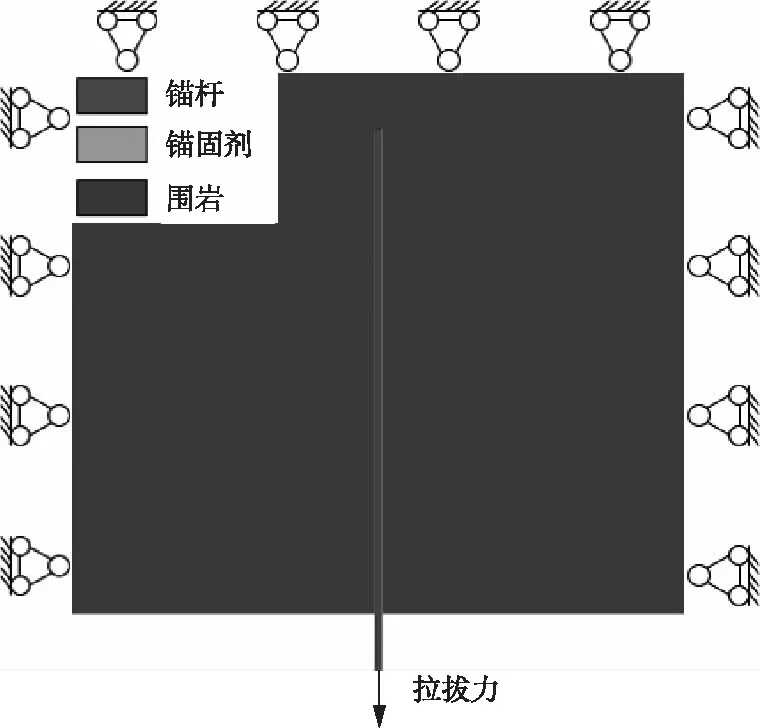
圖4 樹脂錨桿模型剖面圖Fig.4 Resin anchor model profile

表2 模型中材料的力學參數

分別取荷載為10、20、40、60、80 kN，分析在不同荷載下錨桿的傳遞機理，分析圍巖的應力分布規律以及塑性區變化情況。

2.2 模擬結果及分析

通過實驗可以得到圍巖在不同拉拔力條件下的變形情況。取鉆孔附近圍巖的塑性區分布如圖5所示。隨著拉拔荷載的增加，巖體的塑性區呈倒錐形逐漸擴大，逐漸向孔深處蔓延。在拉拔荷載小于60 kN時，塑性區呈現為標準倒錐形；當拉拔荷載為80 kN時，塑性區已蔓延至孔底，錨桿的拉拔使周圍巖體均處于破壞狀態。

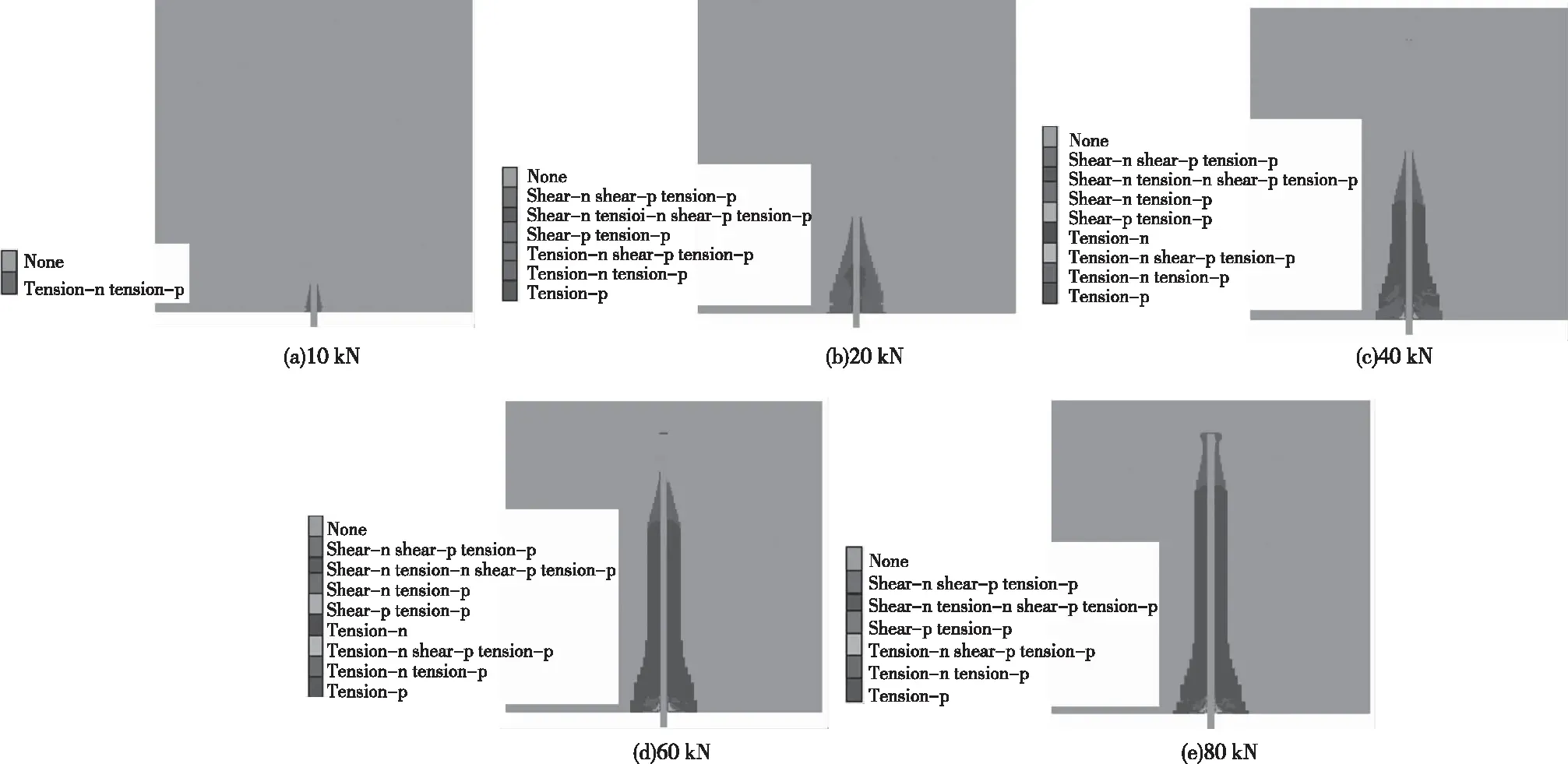
圖5 不同拉拔荷載下的圍巖塑性區分布Fig.5 The plastic zone distribution maps of surrounding rock under different drawing loads

分析在不同拉拔荷載作用下圍巖剪應力的應力分布(圖6)。當拉拔力較小時，圍巖剪應力主要分布在孔口有限的范圍內，沿著桿體呈非線性向底部分布，且孔口位置的圍巖剪應力最大；隨著拉拔力的增大，圍巖剪應力作用的范圍沿著桿體向孔底擴散，但圍巖剪應力的分布趨勢并未改變。與塑性區相對應，當拉拔荷載小于80 kN時，剪應力從孔口向孔底擴散，最大剪應力位于孔口位置；當拉拔荷載大于80 kN時，剪應力已覆蓋整個孔面，最大剪應力位于孔口處。與圍巖剪應力相對應，錨桿的軸力如圖7所示，孔口端部錨桿所受軸力最大，逐步向孔底擴散。

圖6 不同拉拔荷載下圍巖的剪應力分布(單位：MPa)Fig.6 Shear stress distribution maps of surrounding rocks under different drawing loads(Unit：MPa)

圖7 不同拉拔荷載下的錨桿軸力分布(單位：MPa)Fig.7 Axial force distribution maps of anchor under different drawing loads(Unit：MPa)

圍巖剪應力在錨固段端部時較小，隨后急劇增大至峰值后又逐漸減小。圍巖剪應力在圍巖前端約三分之一的范圍內承受的剪應力較大。軸向力與之相對應，如圖8所示，在孔口三分之一的部位軸向力迅速減小70%～80%，之后緩慢減小至零。由此可見，圍巖主要承載剪應力的區域為錨固段前端，主要分布于錨固段前端，錨桿錨固時的錨固力主要由該區域承擔，該部位為錨桿主要受力區，錨桿強度的大小主要取決于錨固段前端錨桿強度。模擬分析結果與1.3節工程實例中的結論相一致。

圖8 監測錨桿軸力分布Fig.8 Monitoring bolt axial force distribution

3 結論

1)拉拔實驗中，圍巖剪應力呈負指數分布。圍巖剪應力值在孔口位置為0，距離孔口50 mm范圍內剪應力急劇增大至峰值，之后緩慢減小并在孔底位置趨近于0。錨桿軸力分布與剪應力分布相對應，樹脂錨桿的軸向力在孔口處最大，在孔口三分之一的部位軸向力減小70%～80%，最后逐漸趨于零。

2)拉拔荷載的增加使巖體的塑性區以標準倒錐形逐漸由孔口向深部蔓延，當拉拔荷載為80 kN，塑性區已蔓延至孔底，錨桿的拉拔使周圍巖體均處于破壞狀態。

3)拉拔試驗的數值模擬與理論分析進行相互驗證。并將分析結果應用于某金礦樹脂錨桿的支護設計中，該分析得出樹脂錨桿支護強度的大小主要取決于錨桿錨固段端部強度的大小，結果為礦山支護設計提供了理論依據。