Delaunay三角網生長法的優化與應用

韋云艦，盧 中

（1.甘肅省地質礦產勘查開發局第三地質礦產勘查院，甘肅 蘭州 730050；2.中交第二航務工程勘察設計院有限公司，湖北 武漢 430071）

工程測量中常采用不規則三角網（TIN）模型來表示地形。為了使三角形能更好地對地形變化進行擬合，應盡量使三角形接近等邊，三角形的最小角最大。經證實，一般情況下在所有可能形成的三角網模型中，Delaunay三角網是最優的。由于Delaunay三角網構網復雜，因此不同算法的執行效率存在較大差異。現有較成熟的Delaunay三角網構網方法主要包括三角網生長法、逐點插入法和分治法3種，各有利弊[1-4]。本文以經典Delaunay三角網生長法為基礎，對三角形尋找第三點的方法進行了優化，明顯提升了該方法的執行效率；并將三角網成果用于提取道路斷面，分析了其實用性。

1 經典Delaunay三角網生長法

Delaunay三角網生長法是基于Delaunay三角網的空圓特性的，即Delaunay三角網中任意一個三角形的外接圓內不存在其他點。基于此， Delaunay三角網生長法的構網步驟為：①任選點庫中的一個點P1；②遍歷點庫，尋找距點P1最近的點P2，并與之相連構成第一邊，添加到邊庫中；③遍歷點庫，尋找第三點與P1、P2構成三角形，使之外接圓滿足空圓特性，并將第三點與P1、P2的連線添加到邊庫中，相應的三角形添加到三角形庫中（如ΔP1P2P4外接圓內存在點P3，不滿足條件，而ΔP1P2P3外接圓內不存在其他點，滿足條件，如圖1所示）；④遍歷邊庫，判斷各邊兩側是否應構建新的三角形，若邊兩側均存在三角形或不存在其他點，則該邊已構建完成，否則重復步驟③、步驟④，直至所有邊均構建完成，如圖2所示，如邊P1P2左側存在ΔP1P2P3、右側無點，則無需構造新的三角形，該邊已構建完成，邊P1P3右側存在ΔP1P2P3、左側無三角形且仍存在其他點，則應繼續尋找第三點構建新的三角形。

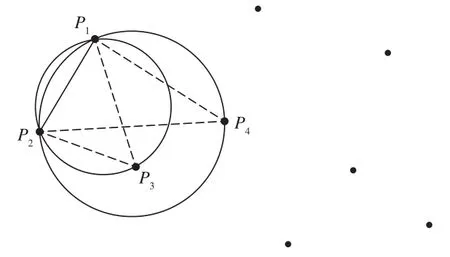
圖1 Delaunay三角網構建過程

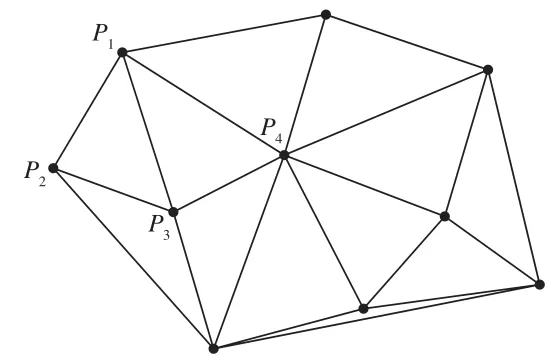
圖2 Delaunay三角網構建結果

2 算法優化

由Delaunay三角網的構建過程可知，其耗時操作主要在尋找第三點上，因此算法優化主要用于簡化第三點的尋找過程[5-9]。

2.1 排除封閉點

封閉點的概念由賀全兵[10]等提出，在尋找第三點構網的過程中會不斷產生封閉點。以P1為起始點經過3次遍歷后的結果如圖3所示，此時點P3已被三角形所包圍，稱之為封閉點。封閉點將不再參與下一次遍歷邊庫尋找第三點的過程，因此第4次遍歷前可將點P3從備選點庫中移除。通過動態地排除封閉點，可將第三點的備選范圍不斷縮小，以減少尋點時間。

尤磊[11]等在封閉點概念的基礎上提出了以優先點為中心的Delaunay三角網構建方法，是對排除封閉點方法的進一步優化。具體方法是對于新增的三角形角點Pi，優先擴展以Pi為角點的邊，待Pi成為封閉點后將其從備選點庫中移除，此時稱Pi為優先點。采用該方法能更快地將優先點變為封閉點，優化備選點庫，提高構網效率。

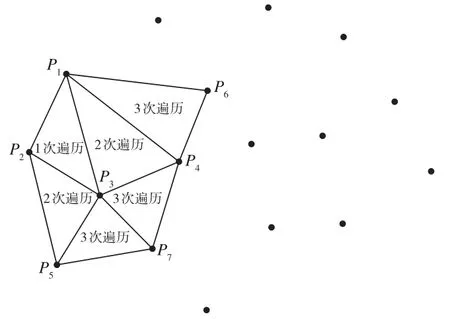
圖3 封閉點示意圖

2.2 第三點排序

由Delaunay三角網的空圓特性和最大最小角特性可知，第三點大概率會出現在前兩點附近（點集邊緣的三角形除外）。如圖4所示，在進一步尋找P1P6左側三角形的第三點時，第三點大概率會是距離P1P6中點（設為P1-6）最近的P8、P9、P10之一，而不會是遠處的Pn、Pn+1。由于點集中點的順序是無規律的，每次判斷某點是否為第三點時，均需遍歷點集中的其他點是否在第三點的外接圓內，極為耗時，因此本文算法在每次尋找第三點時均會根據備選點到前兩點的距離進行排序，即最靠近P1P6中點P1-6的點優先進行空圓判斷。設點P1、P2、…、Pn坐標依次為（X1,Y1）、（X2,Y2）、…、（Xn,Yn），即P1-6P8長度可表示為：

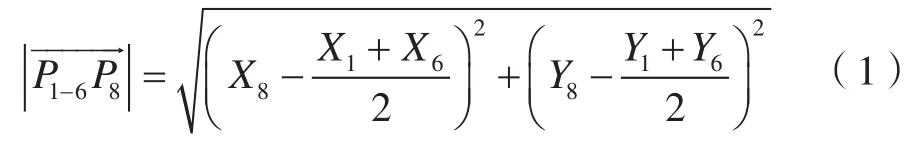
本文采用冒泡排序法選取距離前兩點最近的i個點優先進行空圓判斷，尋找第三點。由于每次排序均需根據式（1）計算所有備選點到前兩點中點的距離，考慮到對于計算機而言，浮點類型數據的加減法執行效率比乘除法高數十倍，因此以式（2）代替式（1），可近似篩選距離最近的點，可大幅提升冒泡排序效率。

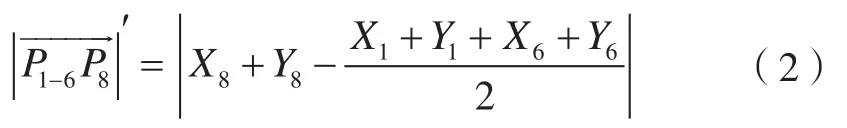
冒泡排序法需重復遍歷待排序的數組，依次對比相鄰元素，若相鄰元素排序錯誤則交換其順序，因此選取距離最近的i個點需進行i次遍歷。遍歷次數越大，即篩選的最近點越多，目標點出現在最近點中的概率越大，但排序耗時也越長，因此需測試選擇最佳遍歷次數。本文選用10 000個不規則排序的三角網點作為測試數據，測試了遍歷次數、最近點包含目標點的概率、構網時間三者的關系，結果如表1所示，可以看出，當篩選的最近點逐漸增多時，最近點包含目標點的概率將迅速增大，但難以達到100%，此時最近點不包含目標點的情況主要出現在三角網邊緣的狹長三角形中。以圖5為例，在尋找P1P2右側的Delaunay三角形時，目標點為Pn，而采用排序法優先選取的最近點依次為P3、P4、P5、P6等，這種情況在三角網邊緣難以避免，因此遍歷次數應以三角網的構網時間為依據，取最佳遍歷次數為7。

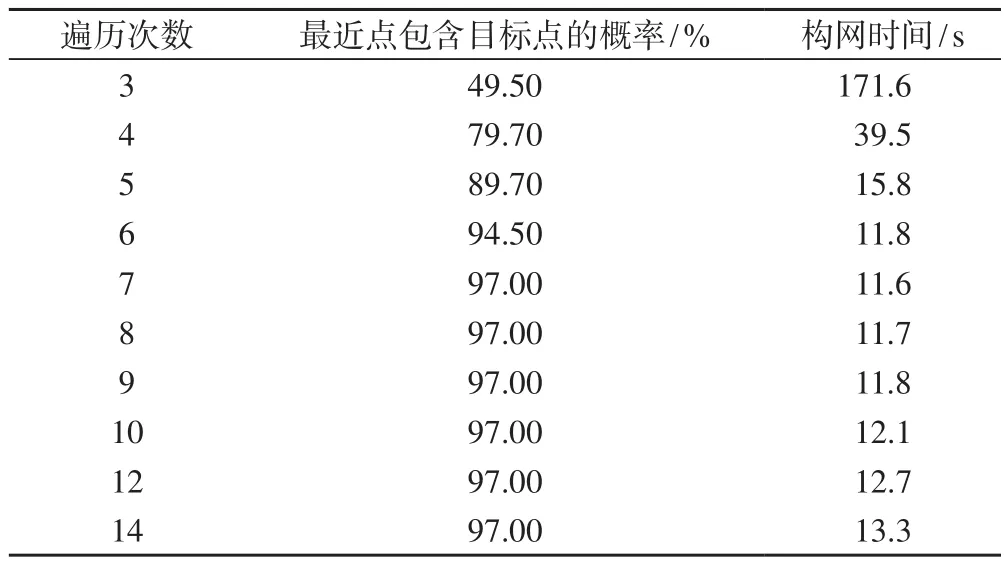
表1 三角網生成時間匯總表（取樣點為10 000）

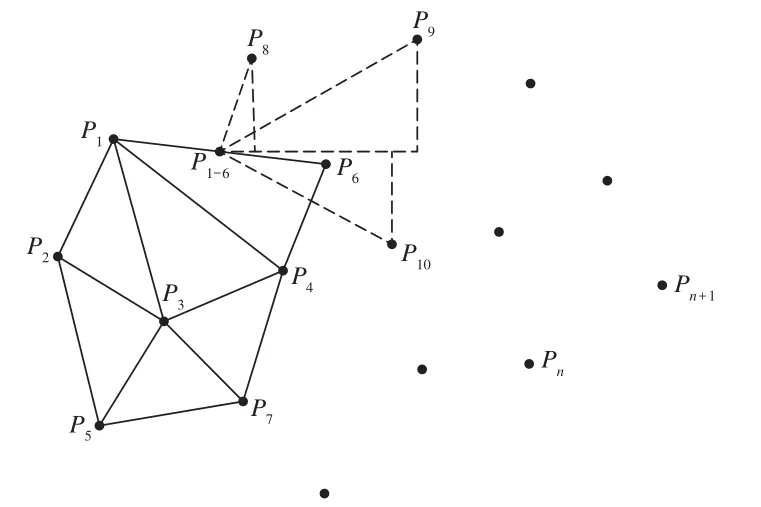
圖4 第三點排序方法

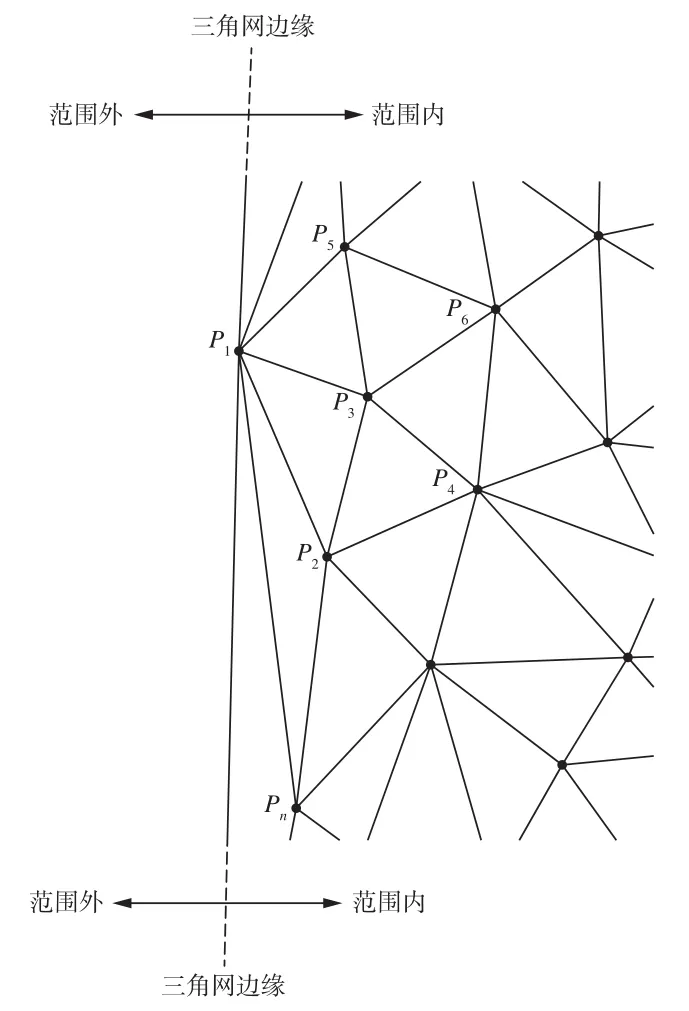
圖5 三角網邊緣構網示意圖

2.3 算法執行效率比較

本文采用優化前后的Delaunay三角網生長法對不同數量的樣本點進行處理，并對構網時間進行匯總，結果如表2所示，可以看出，優化后的Delaunay三角網生長法的執行效率得到了明顯提升，隨著樣本點數量的增加，效率提升效果將更為明顯。程序的執行效率受編程語言、計算機性能、采樣點排序等諸多因素影響，本文采用Java語言編寫程序，程序運行于Windows10 64位系統中，計算機處理器為Intel Core i5 2.30GHz，內存為8G，采樣點為完全隨機樣本。

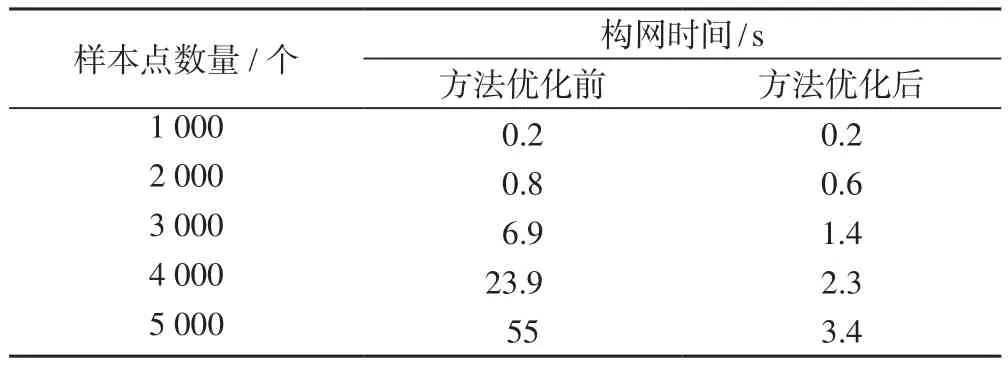
表2 樣本數量與構網時間匯總表

3 基于Delaunay三角網的斷面提取方法

由地面高程點構成的Delaunay三角網可用于表示地形起伏，當高程點密度足夠時，可在三角網的基礎上內插指定點位高程。基于此，可在Delaunay三角網的基礎上提取道路橫斷面，具體方法為：①根據設計斷面端點坐標和點間距計算斷面節點坐標；②根據節點平面坐標判斷節點所在三角形；③根據三角形角點三維坐標確定三角形所在平面方程，再代入斷面節點平面坐標，計算節點高程。

為了提高程序執行效率，判斷節點是否在三角形內時采用向量法。如圖6所示，判斷斷面節點Ti是否在ΔP1P2P3內時，可將向量表示為向量和向量的矢量和，即

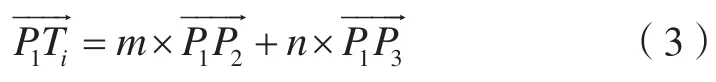
當m、n滿足以下3個條件時，可判定節點Ti在ΔP1P2P3內。

設ΔP1P2P3所在平面方程為Z=A×X+B×Y+C，Pi點的三維坐標為(Xi,Yi,Zi)，代入平面方程解得：

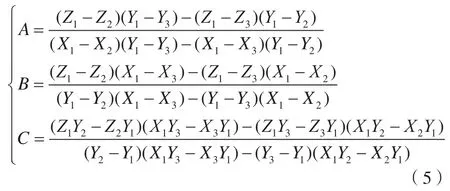
代入節點Ti的平面坐標(XTi,YTi)，得到其高程，則有：

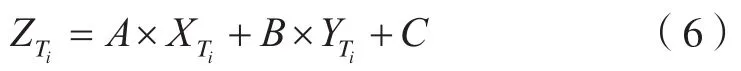
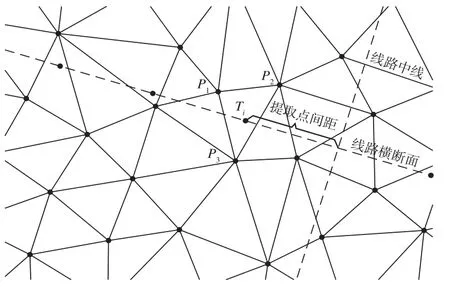
圖6 斷面提取過程示意圖

4 案例分析

本文的實驗數據源自上饒至浦城高速公路（江西境內）的新建工程，項目定測外業時間緊、任務重，且存在大面積山區密林地段。定測時正值冬季，樹葉相對稀少，利于激光穿透植被，常規測量手段施測困難，因此項目的橫斷面測量采用機載激光雷達施測。機載激光雷達外業作業平均航高為200m，點云平均密度小于10cm。在測區范圍內，選取合適的特征點利用RTK進行檢測，結果如表3所示，可以看出，激光雷達數據可靠，可滿足斷面測量精度需求。

本文采用均值法提取平均點密度為3m的點云用于生成三角網，并提取道路橫斷面，將提取的橫斷面成果與實測橫斷面進行對比，結果如圖7所示，可以看出，采用程序提取的橫斷面成果與實測成果吻合良好，誤差主要集中于變坡處，若適當提高橫斷面節點的提取密度可使變坡處的擬合效果更好。本文提取橫斷面節點的間距為1m，橫斷面提取結果與RTK實測結果相比最大較差小于0.2m，可滿足精度需求，方法具備可行性。

圖7 橫斷面示意圖

表3 激光雷達數據檢測結果統計表

5 結 語

本文在Delaunay三角網生長法的構網過程中，通過排除封閉點和第三點排序的方法對原有方法進行了優化。經驗證，優化后的Delaunay三角網生長法的執行效率得到了明顯提升。本文利用優化后的Delaunay三角網生長法將機載激光雷達施測的高密度點云數據生成三角網，并在此基礎上對道路橫斷面數據進行提取，經RTK檢測可知，提取的橫斷面數據成果精度良好，方法具備可行性。