感應電機電流環非線性積分滑模控制策略

王 勃 王天擎 于 泳 羅 成 徐殿國

感應電機電流環非線性積分滑模控制策略

王 勃 王天擎 于 泳 羅 成 徐殿國

（哈爾濱工業大學電氣工程及自動化學院 哈爾濱 150001）

滑模控制器能有效提升感應電機電流環魯棒性，然而傳統滑模控制存在嚴重的抖振問題，雖然通過引入趨近律能有效降低系統抖振，但仍無法實現系統在有限時間內收斂。為此，該文提出一種感應電機非線性積分滑模電流控制器，在削弱系統抖振的同時，實現了定子電流誤差在有限時間內收斂。首先，設計非線性積分滑模面，有效避免了傳統積分滑模面中初始誤差大而導致的積分飽和問題。其次，通過將滑模面的信息引入冪次趨近律，實現控制器對系統狀態的自適應收斂，有效地削弱了系統抖振。最后，對比實驗結果驗證了所提出算法的有效性。

感應電機 電流環 積分滑模控制 有限時間內收斂 抖振

0 引言

感應電機（Induction Motor, IM）矢量控制系統已廣泛應用于先進制造、交通運輸、采礦冶金、家用電器等諸多領域[1-2]。矢量控制通常采用級聯雙閉環結構，包括轉速環和電流環。其中，電流環作為控制系統內環，能夠使定子電流實際值跟蹤給定值，其快速響應能力和魯棒性是轉速外環性能提升的基礎[3-5]。

目前，電流環控制策略可分為線性控制和非線性控制兩大類。線性控制以PI控制為典型代表，具有結構簡單、無穩態誤差、便于理論分析等優點[5]。然而傳統PI控制器參數設計依賴電機數學模型。在實際運行過程中，電機參數受環境溫度、磁場飽和程度等影響會發生攝動，導致電流控制性能降低，甚至不穩定。非線性控制包括滯環控制[6]、預測控制[7]、智能控制[8]、滑模控制[9]（Sliding Mode Control, SMC）等。其中，滑模控制無需系統精確模型，具有響應快速、魯棒性強等優點[10-11]。但滑模控制存在由高頻切換控制導致的抖振問題，且系統狀態變量難以在有限時間內收斂[12]。

針對抖振問題，文獻[13]提出了將滑模切換控制函數連續化的方法，但該方法犧牲了滑模控制的強魯棒性。文獻[14]采用邊界層法來削弱系統抖振，但該方法僅能保證系統狀態收斂到以滑模面為中心的較窄邊界層內，只能無限接近而不能收斂到滑模面。文獻[15]提出利用冪次趨近律滑模控制來削弱系統抖振，但未分對收斂時間。文獻[16]提出了一種高階滑模控制，使滑模變量高階導數為零，在理論上消除了抖振，但并未應用到實際系統中。

針對狀態變量無法在有限時間內收斂的問題，文獻[17]提出了一種積分滑模控制，并將其應用于永磁直線同步電機直接推力控制，但其滑模面中包含在實際應用過程中難以直接獲取的狀態誤差微分項。文獻[18]根據Super-Twisting理論設計了永磁同步電機滑模觀測器，利用二階控制律有效削弱傳統滑模觀測器的固有抖振，消除了反電動勢的跟蹤誤差，但并未用于控制器設計。文獻[19]將積分滑模應用于感應電機無速度傳感器帶速重投控制，實現了系統在有限時間內收斂，但該方法仍沿用邊界層法削弱系統抖振，犧牲了系統魯棒性。

因此，抖振與無法在有限時間收斂問題仍是限制滑模控制在感應電機電流環應用的關鍵因素。為此，本文提出了一種非線性積分滑模電流環控制器，創新點主要體現在以下兩方面：①設計基于非線性積分函數的滑模面，實現系統狀態變量的有限時間收斂；②基于非線性積分滑模面，設計冪次趨近律削弱系統抖振。最終，在2.2kW實驗平臺上進行對比實驗，實驗結果驗證了該算法的有效性。

1 感應電機數學模型及控制系統

基于轉子磁場定向（Rotor Field-Oriented Control, RFOC）的感應電機狀態方程可表示為

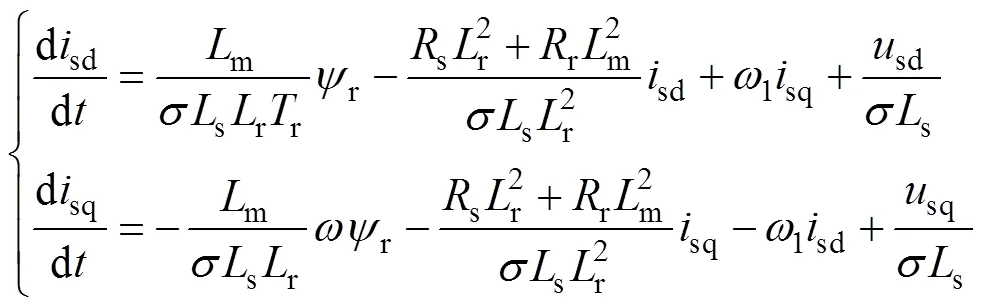
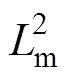
進一步將式（1）用矩陣形式表示為

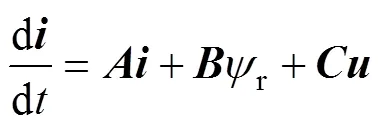
其中

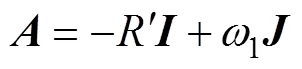
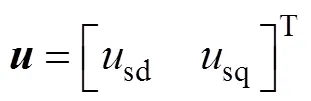
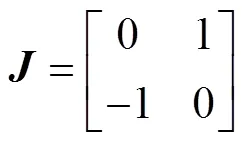
圖1是基于RFOC的感應電機矢量控制系統框圖。整個系統包括感應電機、整流器和逆變器、控制單元。其中，控制單元采用級聯雙閉環矢量控制結構，外環為轉速環，采用PI控制；內環為電流環，采用本文所提出的非線性積分滑模控制，其輸入為轉矩電流參考值isq,ref和勵磁電流參考值isd,ref，其輸出為d、q軸指令電壓usq與usd。

2 傳統滑模電流控制器

PI控制作為電流環最常用的控制策略，能夠實現定子電流無穩態誤差收斂，但電流環PI控制器設計多采用零極點對消的方法，這導致其依賴精確的電機模型[1]。在實際應用中，由于環境溫度變化和磁場飽和效應，電機的電阻和電感都將產生攝動，導致系統模型不匹配，使電流控制性能降低。

相比于PI電流環控制，滑模控制無需系統精確模型，具有對模型不敏感、抗擾動能力強等優點，是一種強魯棒性控制策略[20-24]。本節將給出傳統滑模與冪次趨近律滑模電流控制器設計，并分別對兩種控制下系統狀態收斂時間進行分析。

2.1 傳統滑模電流控制器設計

傳統滑模電流控制的思想是通過切換控制使電流誤差在零附近達到滑動模態，實現定子電流收斂。為此，需要建立定子電流誤差的狀態方程，首先，將參考電流代入式（2）得參考系統為

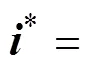
由式（3）與式（2）做差得誤差系統為

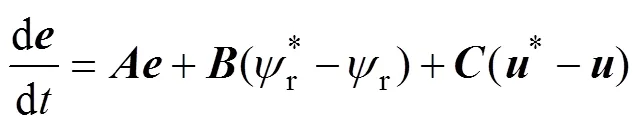
式中，為定子電流誤差，=*-。

滑模控制設計包括滑模面的選取與控制律的設計兩步。選取線性滑模面為

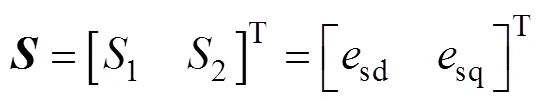
設計滑模控制律為

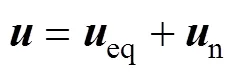
其中

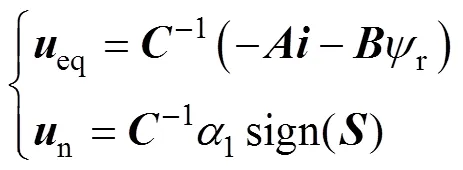
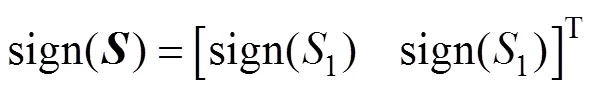
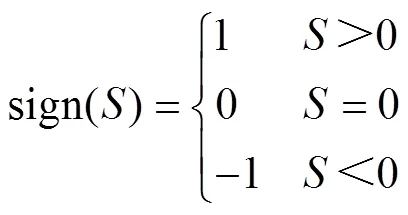
可見，由于控制律中存在切換函數，當系統處于滑模面滑動時會存在嚴重的抖振。

對收斂時間分析，將式（7）中的控制律與式（3）中的同時代入式（4），可得

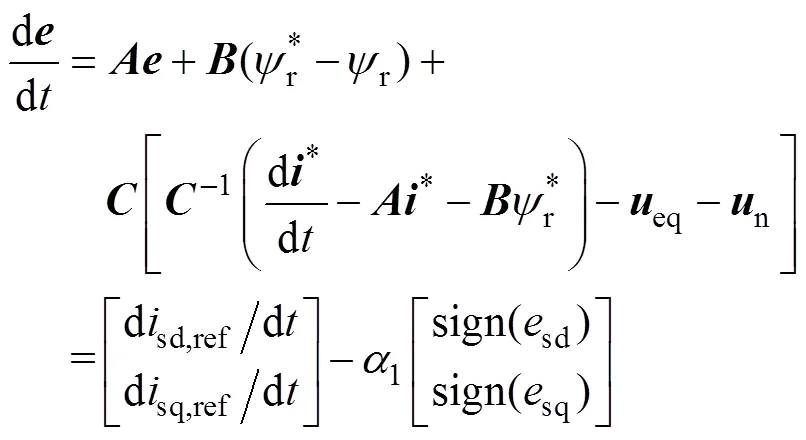
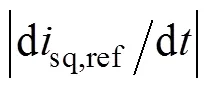
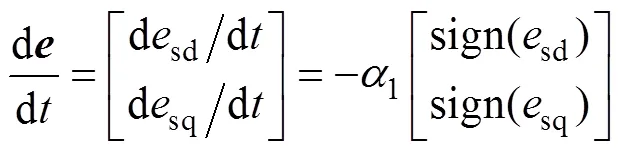
以d軸電流誤差為例進行分析，q軸電流誤差分析方法相同。設初始狀態為sd(0)＞0。由于定子電流誤差的收斂速度為恒定值，可計算出定子電流誤差第一次收斂到零的時間為

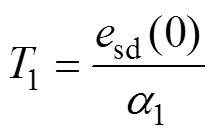
可見，1大小與系統初始狀態以及增益1有關。若1取值較小，則會導致系統到達時間長，甚至無法收斂。若1取值較大，雖然可以減小系統到達時間，但會增加系統抖振。

2.2 冪次趨近律電流控制器

冪次趨近律法是一種有效地削弱抖振和優化系統收斂軌跡方法[13]。電流環冪次趨近律滑模控制律為

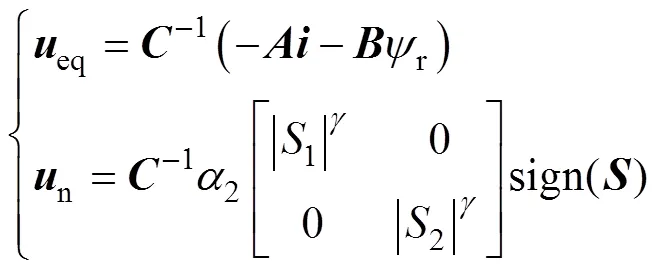
圖2為基于冪次趨近律的滑模電流控制器框圖。由式（12）可見，冪次趨近律法在傳統開關函數的增益中引入定子電流誤差信息，使抖振隨電流誤差減小而減小，有效地削弱了系統抖振。文獻[15, 22]已通過選擇李雅普洛夫函數對冪次趨近律滑模控制的穩定性進行證明。

對收斂時間分析，將式（12）中的控制律代入式（4），可得

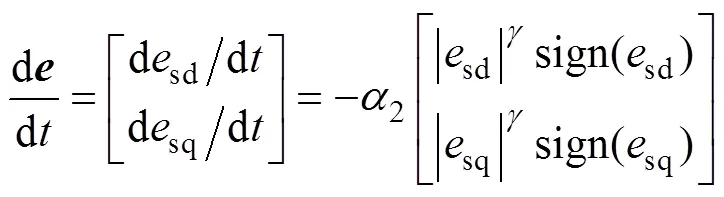
同樣以d軸電流誤差為例進行分析，假設sd的初始值為sd(0)，解微分方程式（13），可得

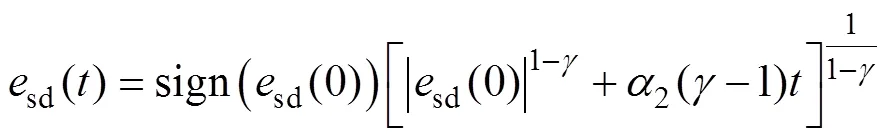
由式（14）可得，當＞1時，定子電流誤差sd()在理論上隨時間的增加而無限趨近于零；當＜1時，sd()隨時間的增加而發散。因此，冪次趨近律無法保證系統誤差在有限時間內收斂到零，即存在有限時間不收斂問題。實質上，雖然通過引入冪次趨近律能夠使控制律連續化，削弱系統抖振，但其本質上仍類似p控制，因此在理論上無法實現有限時間收斂，最終導致系統存在穩態電流誤差。

3 非線性積分滑模電流控制

針對冪次趨近律滑模控制存在的有限時間不收斂問題，本節將提出一種非線性積分滑模電流控制器，通過將所設計的非線性積分函數引入滑模面，并以冪次趨近律結合設計控制律，實現系統狀態在有限時間內收斂，最終消除穩態電流誤差。

3.1 非線性積分函數滑模面設計

傳統積分滑模面[19]可表示為

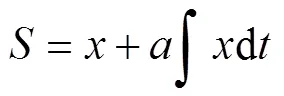
式中，為狀態變量的誤差；為積分項系數，＞0。

由式（15）可見，滑模面中的積分項能夠累計誤差信息，使系統狀態變量在有限時間內收斂。然而，在系統初始狀態時，若實際定子電流與其參考值存在較大誤差，則積分作用會導致滑模面的值突增，產生很大的沖擊，使暫態性能惡化。

為此，本文提出了一種非線性積分滑模面，有

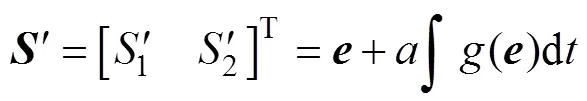
式中，()為所設計的非線性積分函數，有

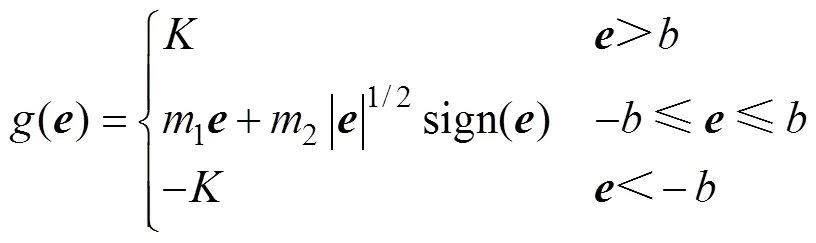
圖3為()的函數圖像，可見，()具有“小誤差放大、大誤差飽和”的特點。因此，所設計的非線性積分滑模面能夠在保證狀態變量有限時間收斂的同時，解決系統暫態性能惡化的問題。

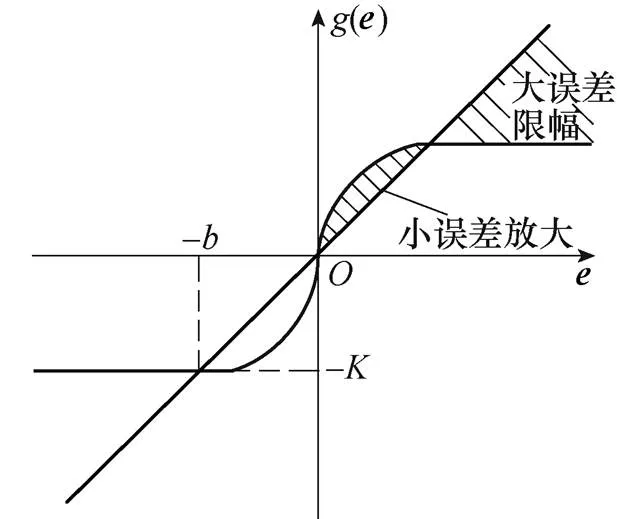
圖3 g(e)函數圖像

3.2 非線性積分滑模控制器設計

基于非線性積分滑模面式（16），設計控制律為

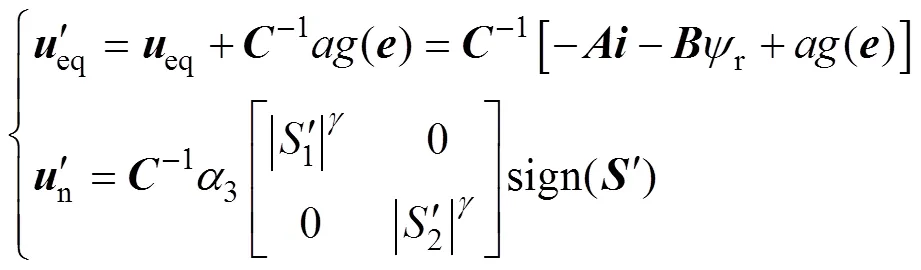
穩定性證明，選取李雅普諾夫函數，有

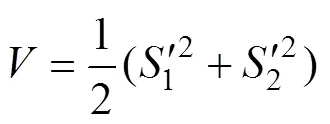
則函數的導數為

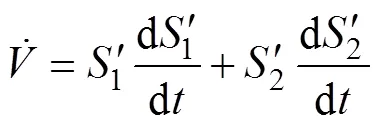
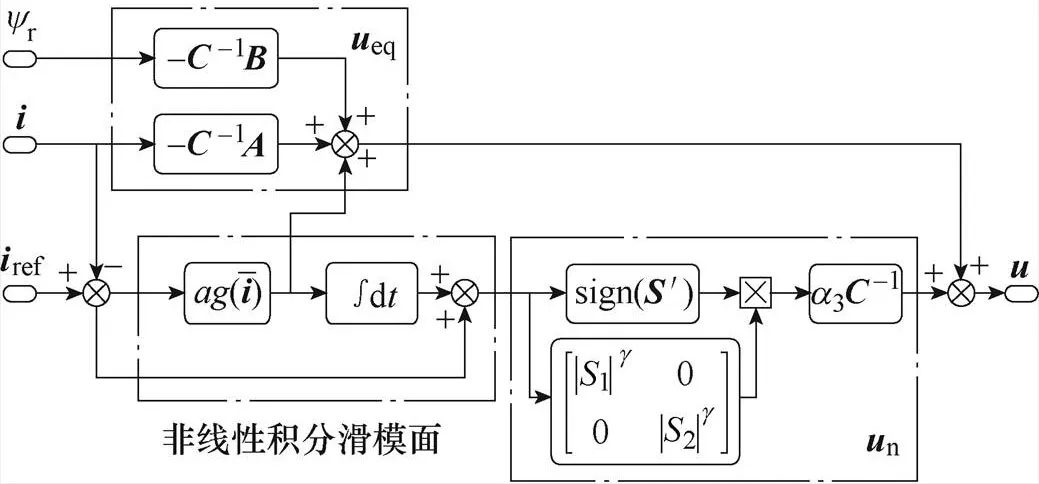
圖4 非線性積分滑模電流控制器框圖

將如式（16）所示的滑模面關于時間求導可得

將式（3）中u與式（19）所設計的控制律代入到式（22）中可得

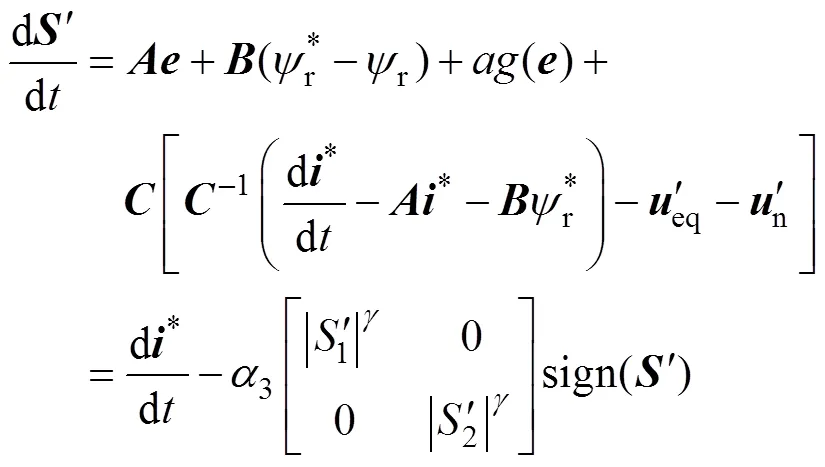
同理，在電機穩定運行時，dsd,ref/d0,dsq,ref/d0。將式（23）進一步代入式（21）中可整理得

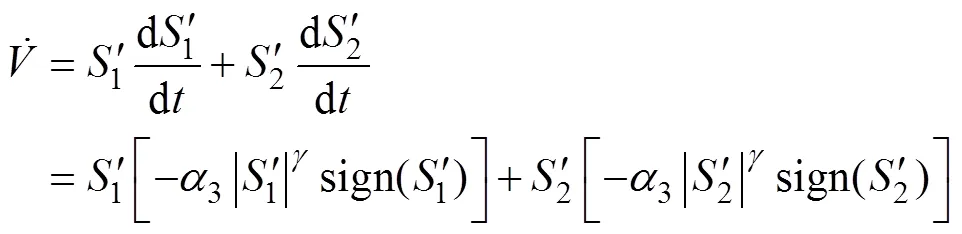
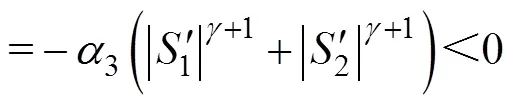
此時，的導數一定為負定，因此該有界系統是穩定的。證明完畢。

3.3 收斂時間分析

由于d、q軸收斂分析情況相同，本文以d軸電流誤差收斂性為例進行分析。設初始狀態為sd(0)，則：

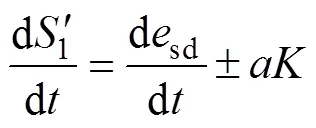
將式（23）進行整理，可得

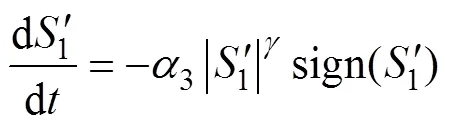
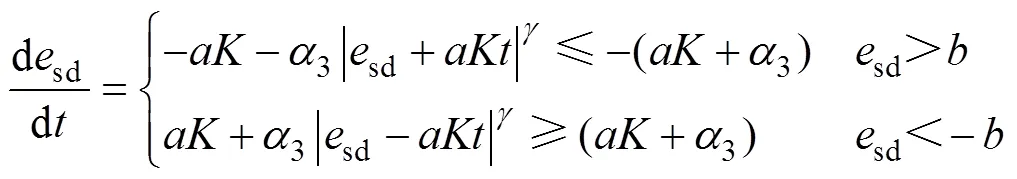
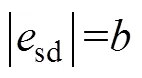
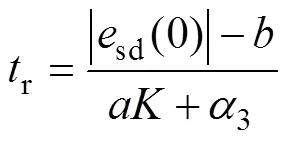
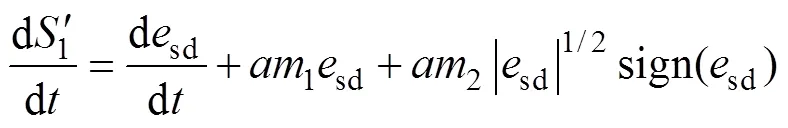
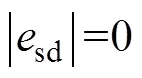
根據上述推導，系統經過小于r+s的時間可使d、q軸電流誤差均收斂到零。因此，非線性積分滑模控制能夠實現系統有限時間收斂，消除穩態電流誤差。

4 實驗驗證

本文采用基于STM32F103 ARM的2.2kW感應電機對拖平臺驗證所提出的算法，實驗平臺如圖5所示，采用兩臺相同規格的感應電機，參數見表1，其中，測試電機用于算法驗證，加載電機用于提供負載轉矩。本文采用雙閉環矢量控制作為基本控制策略，電流環為所提出的非線性積分滑模控制算法。設定勵磁電流sd的參考值為2.5A（50%額定電流），變頻器脈沖寬度調制開關頻率為6kHz。

速度環PI控制器系數選取為：p=2.0，i=450。電流環的參數選取由雅普諾夫穩定性以及收斂速度共同決定的。首先，選取非線性積分滑模面的具體參數,,1,2，步驟如下：根據式（27）與式（29），為了盡可能減小定子電流收斂時間，應盡可能增大。但同時決定了控制律中積分項的大小，當取值過大時，容易造成控制超調。因此，參數的選取應同時考慮系統收斂時間與超調量。為了簡化參數整定過程，選擇=1代入式（17），可得=1+2，其中，為非線性積分函數的限幅值，其選取需同時考慮系統收斂時間與電流誤差，因此選取1≤≤1.5。最后，根據文獻[21]，考慮非線性積分函數的收斂軌跡和速度，最終合理選取參數1和2。

圖5 實驗平臺

表1 感應電機參數

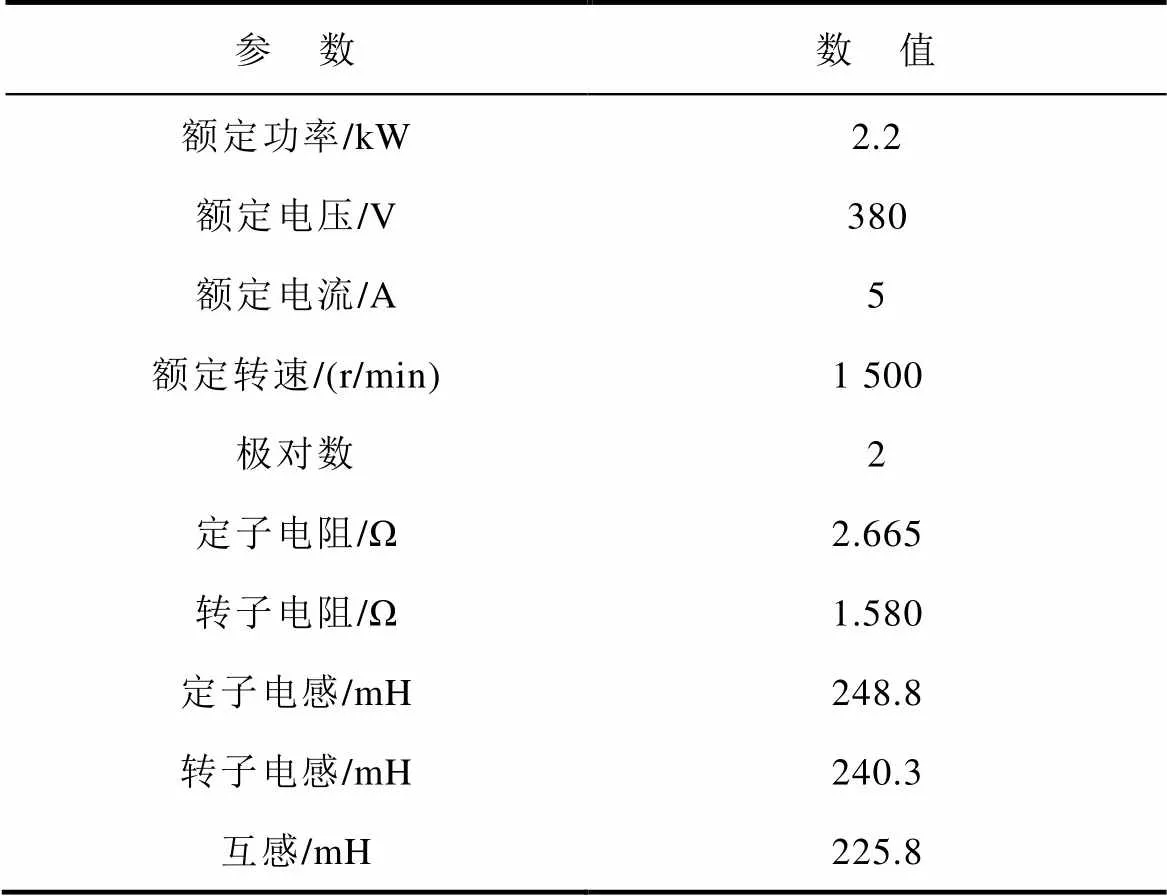
Tab.1 Parameters of induction motor

其次，通過李雅普諾夫穩定性以及抖振大小來確定滑模增益1、2與3的取值。最終實驗中電流環的參數選取如下：非線性積分滑模面中，=18，=1，1=0.4，2=0.8，=1.2。滑模控制增益選取為1=2=3=150。

4.1 全速范圍運行驗證

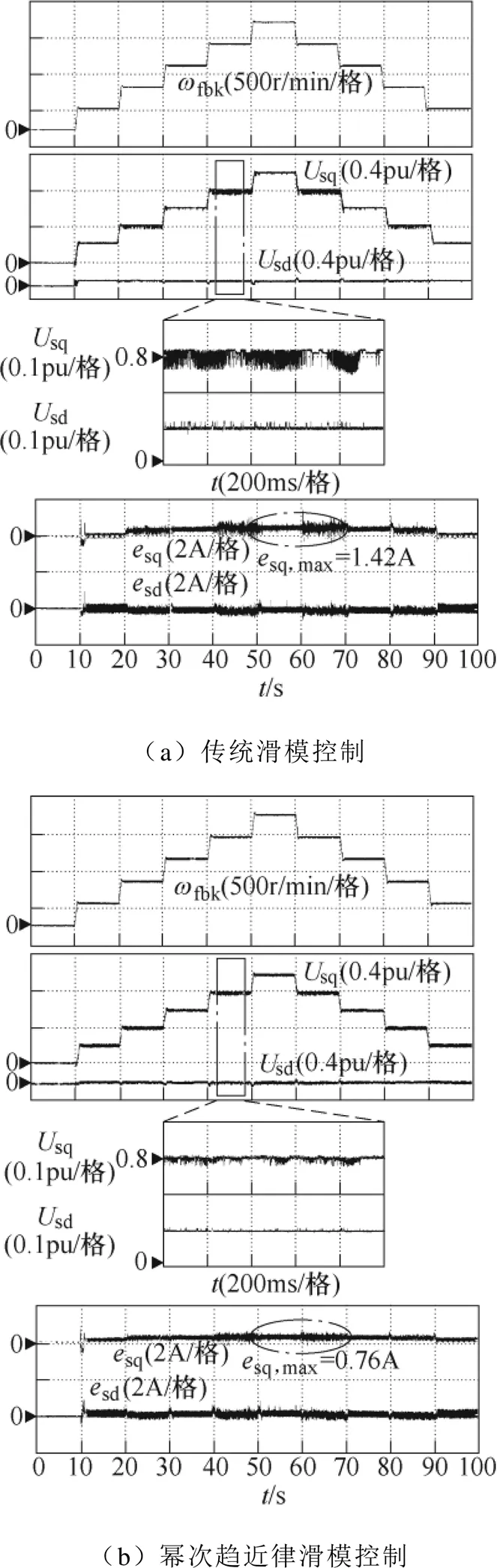
圖6為分別采用傳統滑模控制、冪次趨近律法與所提出非線性積分滑模控制的全速范圍運行對比實驗結果。實驗中，電機在空載下從零速階梯加速到1 500r/min，再階梯降速，并分別給出轉速fbk、指令電壓s和定子電流誤差波形。

由圖6a可見，傳統滑模控制指令電壓存在嚴重抖振，幅值達0.07(pu)，這是由傳統滑模控制中切換函數所導致，并且電流誤差存在隨著轉速升高而增大，最大誤差為1.42A。在圖6b中，采用冪次趨近律滑模控制的指令電壓抖振幅值降低至0.03(pu)，且定子電流穩態誤差減少，但仍未完全消除，最大達到0.76A。對應在圖6c中，采用所提出的非線性積分滑模控制時，抖振幅值降低至0.01(pu)內，并消除了穩態電流誤差。因此，所提出的非線性積分滑模控制能有效削弱系統抖振，并消除穩態電流誤差。

圖7為額定負載工況下上述三種不同方法的加速運行對比實驗結果。實驗中，電機在滿載時從零速加速到900r/min，并給出指令電壓s、定子電流誤差和相電流a的實驗波形。由圖7a和圖7b可見，采用傳統滑模控制和冪次趨近律時，系統存在明顯的穩態電流誤差，誤差分別為1.37A與1.29A。對應在圖7c中，所提出非線性積分滑模控制能有效消除穩態電流誤差，且降低了指令電壓中的抖振幅值。

4.2 額定轉速加速驗證

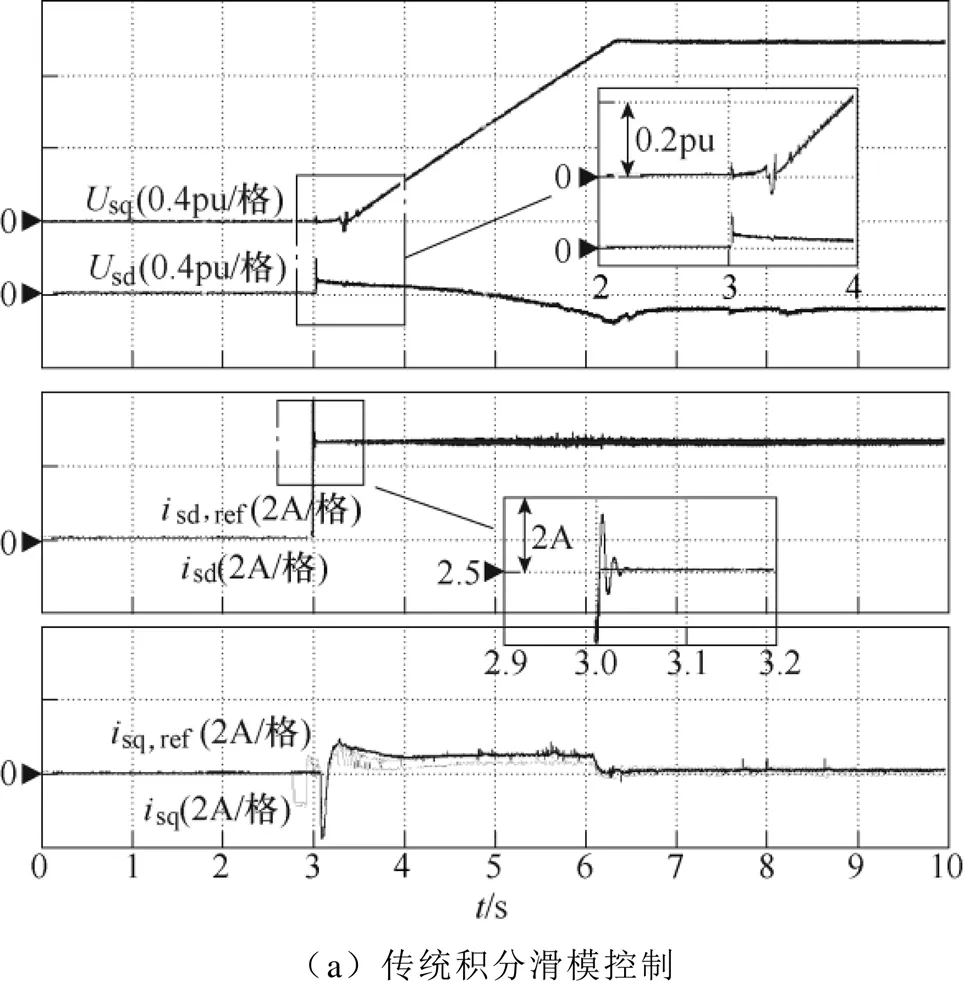
圖8為分別采用傳統積分滑模控制與所提出非線性積分滑模控制的系統加速對比實驗結果。該實驗條件為，電機在空載下轉速由0加速到額定轉速1 500r/min。實驗結果表明，兩種方法均能夠實現定子電流有限時間收斂和穩態誤差消除。但如圖8a所示，傳統積分滑模中在暫態過程中滑模面突增，導致系統收斂性能惡化。相比而言，如圖8b所示，所提出的非線性積分滑模面能夠有效解決滑模面突增問題，改善電流環的暫態性能。

4.3 魯棒性驗證

圖9為所提出算法在電機參數攝動時的系統響應。在實際運行過程中，電機參數將隨環境溫度和磁場飽和而改變。根據式（1），電機互感攝動是影響電流環性能的主要因素[9]，為此，本文以互感變化作為參數攝動來驗證所提出方法的魯棒性。為了滿足電機實際運行中互感的最大變化范圍，這里選取0.5m～2.0m作為測試條件。圖9為電機在600r/min工況下互感由0.5m階梯變化至2.0m時系統的響應波形。可見，在電機互感變化過程中，定子電流d、q軸分量出現明顯波動，但該波動能夠很快被抑制。因此，所提出的算法能夠有效抑制互感變化的影響，證明了所提出的非線性積分滑模控制具有良好的參數魯棒性。

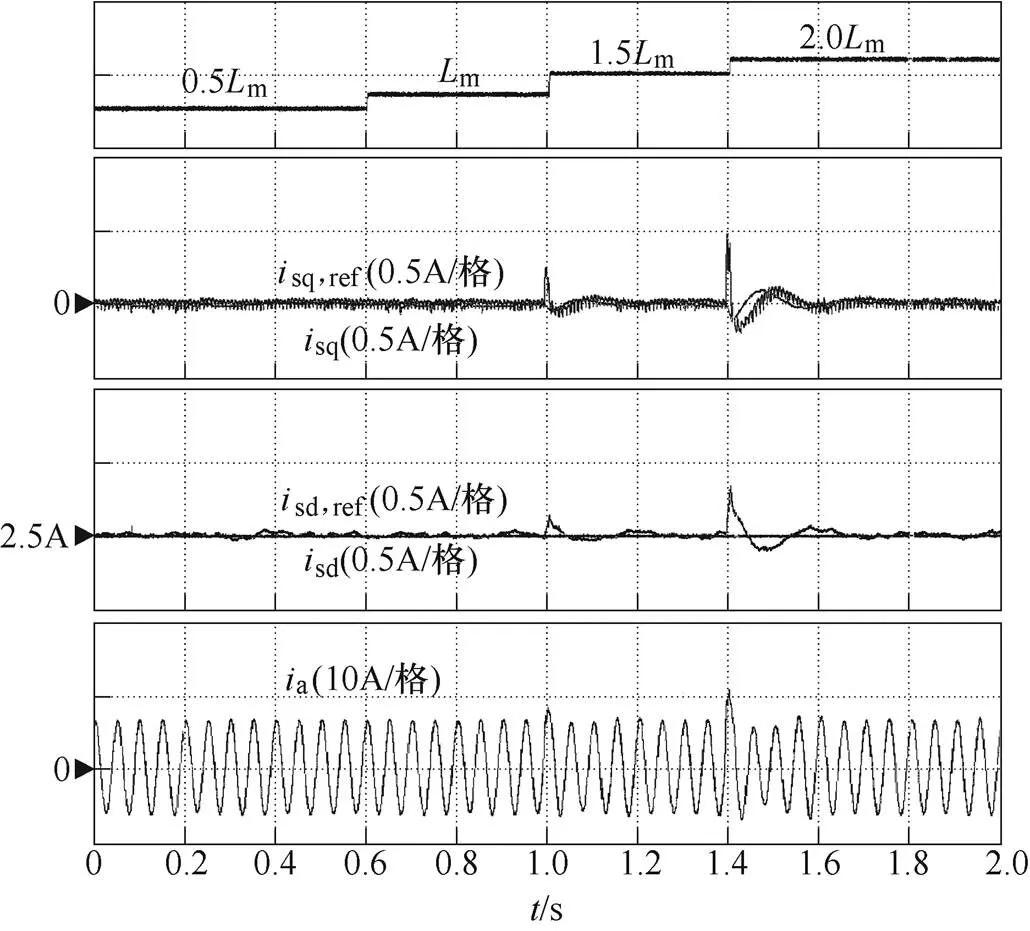
圖9 所提出算法魯棒性測試實驗結果

5 結論

本文所提出的非線性積分滑模有效地解決了傳統滑模控制導致的抖振嚴重問題，實現了定子電流在有限時間內收斂。非線性積分滑模面能夠避免傳統積分滑模面由于初始誤差過大導致的飽和問題，并實現定子電流在有限時間內收斂。所設計的控制律通過結合滑模面與趨近律，能夠有效削弱系統抖振。對比實驗結果證明，所提出的非線性積分滑模控制能夠實現感應電機系統在空載和帶載工況下的無穩態誤差電流控制，并對電機參數攝動具有強魯棒性。

[1] Mishra J, Wang Liuping, Zhu Yuankang, et al. A novel mixed cascade finite-time switching control design for induction motor[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1172-1181.

[2] Yin Zhonggang, Gao Fengtao, Zhang Yanqing, et al. A review of nonlinear Kalman filter appling to sensorless control for AC motor drives[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 351-362.

[3] Fang Xiaochun, Tian Zhongbei, Li Hua, et al. Current closed-loop control and field orientation analysis of an induction motor in six-step operation for railway applications[J]. IET Power Electronics, 2019, 12(6): 1462-1469.

[4] 賀虎成, 孫磊, 張玉峰, 等. 基于矢量控制的異步電機自抗擾控制[J]. 電機與控制學報, 2019, 23(4): 120-125.

He Hucheng, Sun Lei, Zhang Yufeng, et al. Asyn- ronous motor active disturbance rejection control based on vector control[J]. Electric Machines and Control, 2019, 23(4): 120-125.

[5] 齊麗英, 王琛琛, 周明磊, 等. 一種異步電機的電流環解耦控制方法[J]. 電工技術學報, 2014, 29(5): 174-180.

Qi Liying, Wang Chenchen, Zhou Minglei, et al. A decoupling current control scheme for induction machine controllers[J]. Transactions of China Elec- trotechnical Society, 2014, 29(5): 174-180.

[6] Gauri A, Vinod B, Shiny G. Vector control method for induction motor drive based on hysteresis controller and pi controller comparative study[C]// 2019 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 2019: 1-6.

[7] 齊昕, 吳文昊, 吳琳, 等. 基于時間輔助信息的感應電機預測電流控制[J]. 中國電機工程學報, 2019, 39(16): 4927-4934, 4995.

Qi Xin, Wu Wenhao, Wu Lin, et al. Predictive current control of induction machines based on time auxiliary information[J]. Proceedings of the CSEE, 2019, 39(16): 4927-4934, 4995.

[8] 金鴻雁, 趙希梅. 基于Sugeno型模糊神經網絡和互補滑模控制器的雙直線電機伺服系統同步控制[J]. 電工技術學報, 2019, 34(13): 2726-2733.

Jin Hongyan, Zhao Ximei. Dual linear motors servo system synchronization control based on Sugeno type fuzzy neural and complementary sliding mode controller[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2726-2733.

[9] Wang Bo, Dong Zhen, Yu Yong, et al. Static- errorless deadbeat predictive current control using second-order sliding-mode disturbance observer for induction machine drives[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2395-2403.

[10] Chalanga A, Kamal S, Fridman L, et al. Implementation of super-twisting control: super-twisting and higher order sliding-mode observer-based approaches[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3677-3685.

[11] Meng Zhiqiang, Shao Wu, Tang Jie, et al. Sliding- mode control based on index control law for MPPT in photovoltaic systems[J]. CES Transactions on Elec- trical Machines and Systems, 2018, 2(3): 303-311.

[12] 王建美. 不確定非線性系統的滑模控制及其在永磁同步電機中的應用[D]. 秦皇島: 燕山大學, 2018.

[13] Yin Zhonggang, Zhang Yanqing, Tong Xiangqian, et al. Model predictive control using globe exponential reaching law sliding mode design method for induction motor drives[C]//2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 2559-2563.

[14] 張希, 陳宗祥, 潘俊民, 等. 永磁直線同步電機的固定邊界層滑模控制[J]. 中國電機工程學報, 2006, 26(22): 115-121.

Zhang Xi, Chen Zongxiang, Pan Junmin, et al. Fixed boundary layer sliding mode control of permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2006, 26(22): 115-121.

[15] Bartoszewicz A, Le?niewski P. New switching and nonswitching type reaching laws for SMC of discrete time systems[J]. IEEE Transactions on Control Systems Technology, 2016, 24(2): 670-677.

[16] Jin Jianzhao, Ge Suoliang. Finite-time active disturbance rejection control based on high-order sliding mode[C]//2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 2019: 1974-1979.

[17] 原浩, 趙希梅. 基于積分滑模的永磁直線同步電動機直接推力控制[J]. 電工技術學報, 2019, 34(3): 483-488.

Yuan Hao, Zhao Ximei. Direct thrust force control based on integral sliding mode for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 483-488.

[18] 張懿, 吳嘉欣, 韋漢培, 等. 離散型變增益永磁同步電機超螺旋滑模觀測器[J]. 電工技術學報, 2018, 33(21): 4962-4970.

Zhang Yi, Wu Jiaxin, Wei Hanpei, et al. Discrete variable gain super-twisting sliding mode observer for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(21): 4962-4970.

[19] 茍立峰, 王琛琛, 游小杰, 等. 基于積分滑模的感應電機無速度傳感器帶速重投控制策略[J]. 電工技術學報, 2018, 33(24): 5700-5710.

Gou Lifeng, Wang Chenchen, You Xiaojie, et al. A restart method based on integral sliding mode for speed sensorless controlled induction motor[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5700-5710.

[20] Sun Dong, Hu Songyu, Shao Xiaoyin, et al. Global stability of a saturated nonlinear PID controller for robot manipulators[J]. IEEE Transactions on Control Systems Technology, 2009, 17(4): 892-899.

[21] Wang Bo, Luo Cheng, Yu Yong, et al. Antidistur- bance speed control for induction machine drives using high-order fast terminal sliding-mode load torque observer[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7927-7937.

[22] 李鵬. 傳統和高階滑模控制研究及其應用[D]. 長沙: 國防科學技術大學, 2011.

[23] 張國榮, 侯立凱, 彭勃, 等. 柔性多狀態開關反饋線性化滑模控制[J]. 電力系統自動化, 2020, 44(1): 126-133.

Zhang Guorong, Hou Likai, Peng Bo, et al. Feedback linearization sliding mode control strategy for soft open point[J]. Automation of Electric Power Systems, 2020, 44(1): 126-133.

[24] 趙希梅, 劉超, 朱國昕. 永磁直線同步電機自適應非線性滑模控制[J]. 電機與控制學報, 2020, 24(7): 39-47.

Zhao Ximei, Liu Chao, Zhu Guoxin. Adaptive nonlinear sliding mode control for permanent magnet linear synchronous motor[J]. Electric Machines and Control, 2020, 24(7): 39-47.

[25] Teja A V R, Chakraborty C, Pal B C. Disturbance rejection analysis and FPGA-based implementation of a second-order sliding mode controller fed induction motor drive[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 1453-1462.

[26] Wang Liuping, Mishra J, Zhu Yuankang, et al. An improved sliding-mode current control of induction machine in presence of voltage constraints[J]. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1182-1191.

Nonlinear Integral Sliding Mode Control Strategy for Current Loop of Induction Motor Drives

（School of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China）

The sliding mode controller can effectively improve the robustness of induction motor (IM) current loop. However, the conventional sliding mode controller has serious chattering problems. Although the chattering can be effectively suppressed by introducing the reaching law, the system state variable cannot achieve finite-time convergence. To address this problem, this paper proposes a nonlinear integral sliding mode current controller for IM drives. The proposed approach can suppress the system chattering and achieve finite-time convergence simultaneously. Firstly, a nonlinear integral sliding surface is designed to avoid the integral saturation problem caused by large initial error. Secondly, the adaptive convergence of state variable can be achieved by introducing the information of sliding surface into the control law, which effectively weakens the system chattering. The experimental results verify the effectiveness of the proposed method.

Induction motor, current loop, integral sliding mode control, finite-time convergence, chattering

TM341

10.19595/j.cnki.1000-6753.tces.200250

國國家科學基金（51690182, 51807038）、黑龍江省自然科學基金（YQ2020E018）、中國博士后科學基金（2018M630354, 2019T120267）、黑龍江省博士后（YQ2020E018）和中央高校基本科研業務費專項資金（HIT.NSRIF.2019025）資助項目。

2020-03-11

2020-08-14

王 勃 男，1987年生，副教授，博士生導師，研究方向為交流電機控制、現代控制理論及應用等。E-mail: wangbohit@hit.edu.cn

于 泳 男，1974年生，教授，博士生導師，研究方向為交流電機控制、故障診斷及容錯控制等。E-mail: yuyong@hit.edu.cn（通信作者）

（編輯 崔文靜）