基于果蠅算法的多邊形柱狀熱分析模型結構化網格優化劃分方法

郭宇軒 張小平 劉東浩 張 鑄 朱廣輝

基于果蠅算法的多邊形柱狀熱分析模型結構化網格優化劃分方法

郭宇軒1,2張小平1,2劉東浩1,2張 鑄2朱廣輝3

（1. 湖南科技大學海洋礦產資源探采裝備與安全技術國家地方聯合工程實驗室 湘潭 411201 2. 湖南科技大學信息與電氣工程學院 湘潭 411201 3. 湘潭電機股份有限公司 湘潭 411101）

針對交流牽引電機轉子導條等多邊形柱狀熱分析模型結構化網格劃分質量不高的問題，提出一種結構化網格優化劃分方法。建立交流牽引電機熱分析的求解域模型，確定交流牽引電機多邊形柱狀模型的四邊形區域質量計算方法，提出一種基于內置四邊形的多邊形柱狀模型四邊形區域劃分方法，并采用果蠅優化算法（FOA）對各分區方式的綜合質量進行優化以獲得相應的最佳分區方式，再通過有限元法對其效果進行仿真驗證，同時與傳統結構化網格劃分法進行對比仿真分析，最后通過實驗對上述分析作進一步的實驗驗證，結果表明，該文所提出的結構化網格優化劃分方法較傳統結構化網格劃分法顯著提升了交流牽引電機多邊形柱狀模型的網格劃分質量，從而有效提高了交流牽引電機熱分析的準確性，具有較好的應用價值。

交流牽引電機 多邊形柱狀熱分析模型 結構化網格 優化劃分方法 果蠅優化算法

0 引言

交流牽引電機因具有結構簡單、成本低、維護方便等優點而得到了廣泛應用[1]。然而由于電機在運行中會因各種損耗而使溫度迅速升高[2]，如果溫升過高，則可能會引起轉子導條斷裂、繞組絕緣損壞等故障[3]，因此開展交流牽引電機熱分析研究以降低其溫升將具有重要意義。

目前在有關交流牽引電機熱分析方面已開展了大量研究，提出多種分析方法[4-6]。其中，有限元法以具有邊界適應性好、準確度高等優點而得到了廣泛應用。然而在采用限元法對交流牽引電機進行熱分析時，需對其分析模型進行網格劃分，而網格劃分質量則是影響分析結果準確性的一個重要因素。

而在如何提高交流牽引電機熱分析模型的網格劃分質量方面，目前也已提出多種方法[7-9]，其中，結構化網格劃分法因具有網格質量好、計算速度快等優點而得到了普遍重視。然而該方法只適于規則模型的網格劃分，對于交流牽引電機轉子導條等多邊形柱狀模型來說，該方法難以達到滿意的網格劃分結果。

為此，本文針對交流牽引電機轉子導條等多邊形柱狀分析模型，提出一種基于果蠅優化算法（Fruit Fly Optimization Algorithm, FOA）的結構化網格優化劃分方法。介紹了該網格劃分法的基本原理與具體實現方法，并對其效果進行驗證，同時與傳統結構化網格劃分法進行對比分析，結果證明了該方法的有效性。

1 電機損耗計算及邊界條件界定

1.1 電機損耗計算

交流牽引電機運行時會產生包括定子銅耗、轉子鋁耗、鐵耗、機械損耗及雜散損耗等多種損耗[10]，其總損耗可表示為

式中，Cu為定子銅耗；Al為轉子鋁耗；Fe為鐵耗；fw為機械損耗；s為雜散損耗。

1.1.1 定子銅耗

定子銅耗計算公式[11]為

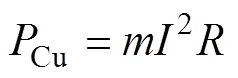
式中，為電機相數；為定子繞組相電流有效值；為定子繞組相電阻。

1.1.2 轉子鋁耗

轉子鋁耗計算公式[12]為

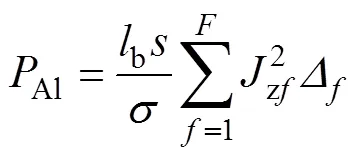
式中，b為轉子導條長度；為電機轉差率；為轉子導條電導率；為轉子槽內總單元數；zf為轉子槽內各單元的感應電流密度；為轉子槽內各單元的面積。

1.1.3 鐵耗

鐵耗常用Bertotti鐵耗三項式計算[13]，有

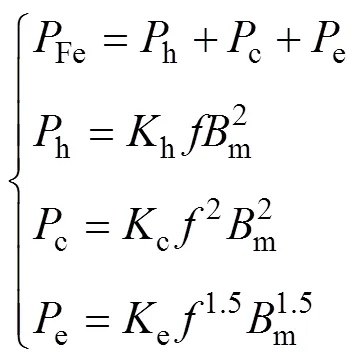
式中，h、c和e分別為磁滯損耗、渦流損耗與異常損耗；m為磁通密度幅值；為磁場頻率；h、c及e分別為磁滯損耗系數、渦流損耗系數及異常損耗系數。

1.1.4 機械損耗

機械損耗計算公式[11]為

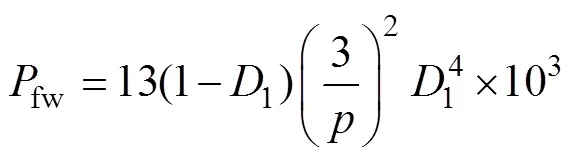
式中，1為定子外徑；為電機極對數。

1.1.5 雜散損耗

交流電機雜散損耗一般按其額定輸入功率的 0.5%計算[14]。

1.2 邊界條件界定

電機運行中產生的熱能將通過機殼與周圍空氣進行熱交換，并最終達到動態平衡，其三類邊界條件的數學表達式[15]為

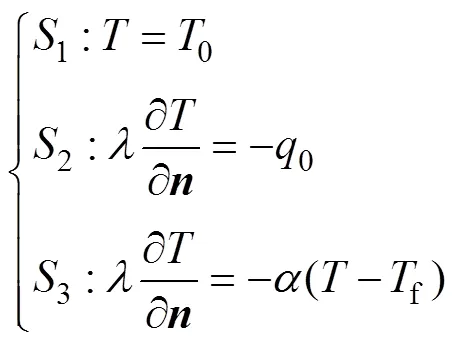
式中，為電機溫度；0為邊界溫度；為導熱系數；為邊界法向量；0為邊界熱流密度；為邊界傳熱系數；f為環境溫度。

其中，邊界傳熱系數的計算公式[16]為

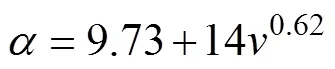
式中，為機殼表面的風速。

而對于定轉子間氣隙的導熱系數來說，則需先計算出氣隙的雷諾數g及其臨界雷諾數cr，再根據兩者的大小來確定其導熱系數[17]，具體為：

（1）分別計算氣隙的雷諾數與臨界雷諾數[18]，有

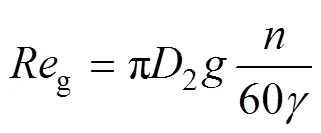
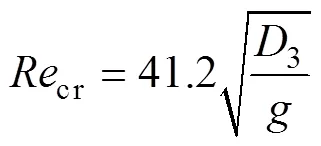
式中，2為轉子外徑；3為定子內徑；為氣隙寬度；為電機轉速；為空氣運動粘度系數。

（2）根據雷諾數g與臨界雷諾數cr的大小，來確定相應的導熱系數，具體為：當g＜cr時，氣隙中的空氣為層流，其導熱系數取空氣的導熱系數；當g≥cr時，氣隙中的空氣為湍流，其導熱系數的計算公式[18]為

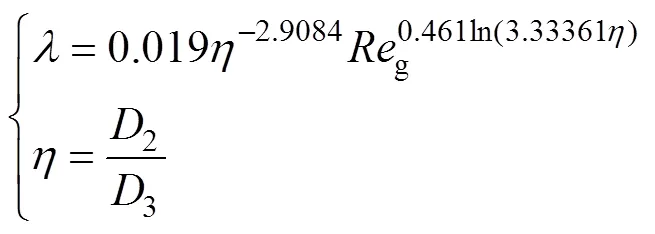
2 建立交流牽引電機求解域模型

在進行交流牽引電機熱分析時，首先需建立其求解域模型，包括熱傳導方程與有限元模型。

2.1 熱傳導方程

在直角坐標系下，交流牽引電機熱傳導方程[19]為

式中，、、分別為、、方向上的導熱系數；為熱源密度。

2.2 有限元模型

由于交流牽引電機軸向對稱，故可只取軸向一半且定、轉子各取一槽來建立其有限元模型；同時為簡化模型結構，根據文獻[20]，將定子繞組多匝導線等效為單一導體，因而所得交流牽引電機三維有限元模型如圖1所示。

圖1 交流牽引電機三維有限元模型

3 多邊形柱狀模型四邊形分區質量計算方法

在采用結構化網格劃分法對交流牽引電機轉子導條等多邊形柱狀模型進行網格劃分前，首先需對其多邊形頂面進行四邊形分區，且分區質量直接影響網格劃分質量；而要獲得高的分區質量，首先需明確相應的分區質量計算方法。

3.1 單四邊形區域質量計算方法

對于單個四邊形區域，本文擬采用雅克比比率法計算其質量[21]。基本原理是：首先由四邊形各頂點坐標分別計算出該四邊形各積分點所對應的雅克比行列式值，分別為

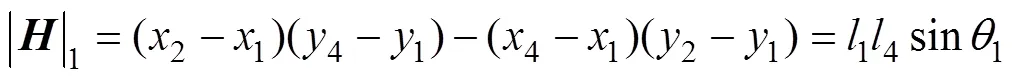
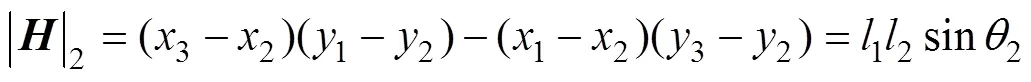
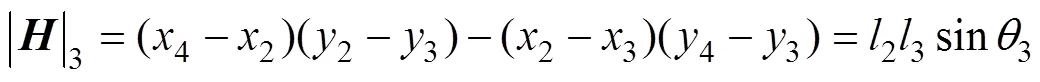
式中，x1～x4為四邊形各頂點的橫坐標；y1～y4為四邊形各頂點的縱坐標；l1～l4為四邊形四邊長；q1～q4為四邊形的四個內角，各參數示意圖如圖2所示。

再根據上述所得各雅克比行列式中的最小值和最大值，即可得到該四邊形的雅克比比率值，其計算公式為

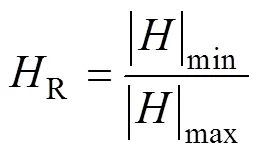
式中，R為四邊形雅克比比率值；min和max分別為四邊形雅克比行列式的最小值和最大值。

根據文獻[21]，四邊形雅克比比率值R越大，則表明該四邊形的質量越好。

3.2 四邊形區域形狀確定方法

由于雅克比比率法只適于凸四邊形的質量計算，即該四邊形各頂點角度均應小于180°；然而實際在對多邊形柱狀模型的多邊形頂面進行四邊形分區時，卻難以保證所得各四邊形區域均為凸四邊形。為此，在針對各四邊形區域質量進行計算前，有必要首先對所得各四邊形區域的形狀進行判斷。為此，提出采用混合積法對各四邊形區域形狀進行判定，具體如下：

（1）令四邊形各頂點編號依次為1、2、3、4，由于混合積計算中各向量均為三維向量，因此設四邊形各頂點豎坐標均為0，即=0。計算混合積、、分別[22]為

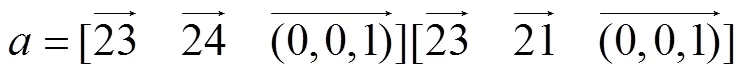
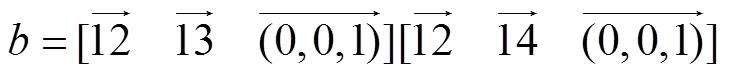
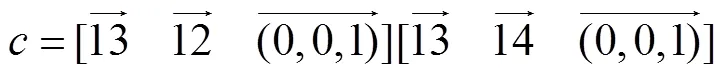
（2）根據上述所得各混合積、、的值，即可判定四邊形各頂點的位置關系，進而判定出該四邊形的形狀，混合積判定示意圖如圖3所示。

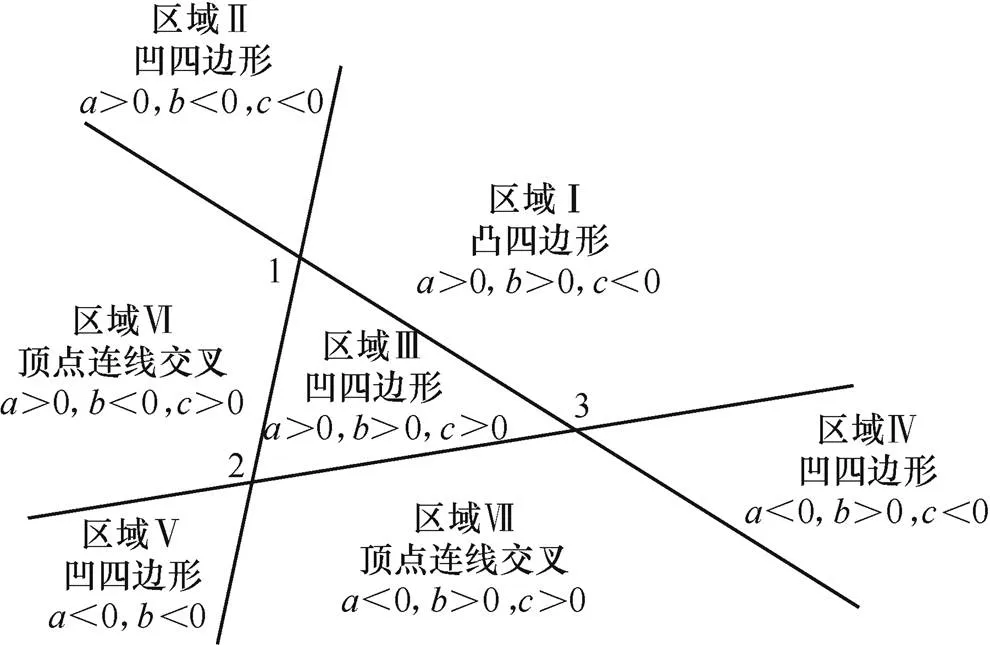
圖3 混合積判定示意圖

圖3中，頂點1、2、3為四邊形的3個頂點，將每個頂點的兩條邊延長，可將平面分為7個區域，即區域Ⅰ區域Ⅶ；再根據混合積的值，即可確定四邊形的第4個頂點處在哪個區域。根據第4個頂點所處不同區域，對應的四邊形有三種形狀，分別為：①若＞0,＞0,＜0，頂點4落在區域Ⅰ中，此時四邊形為凸四邊形；②若＞0,＜0,＜0或＞0,＞0,＞0或＜0,＞0,＜0或＜0,＜0，則頂點4分別落在區域Ⅱ～區域Ⅴ中，此時四邊形均為凹四邊形；③若＞0,＜0,＞0或＜0,＞0,＞0，則頂點4分別落在區域Ⅵ和區域Ⅶ中，此時4個頂點的連線產生交叉。

如以頂點4落在區域Ⅱ中為例，即在區域Ⅱ中任取一點作為頂點4，再將4個頂點依次相連，所得四邊形如圖4所示，可見此時為一個凹四邊形。

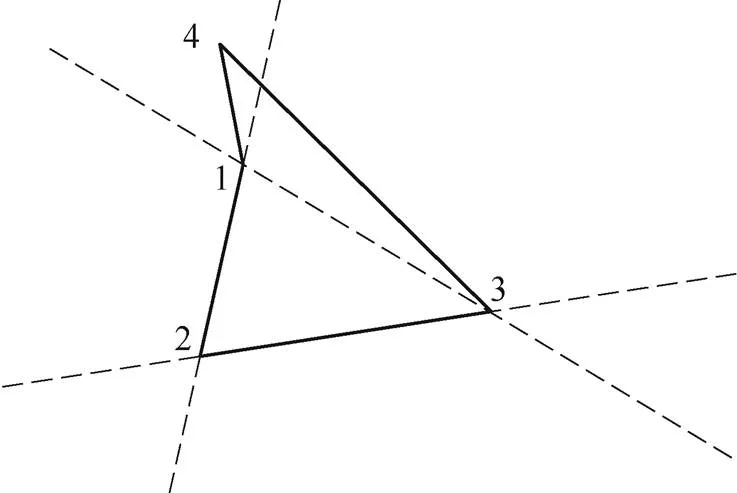
圖4 頂點4落在區域Ⅱ時的四邊形示意圖

通過4個頂點連線來確定相應的四邊形時可能存在上述三種類型，分別為凸四邊形、凹四邊形和連線交叉。

3.3 多四邊形區域綜合質量計算方法

如上所述，在由4個頂點通過連線來確定相應的四邊形時可能存在上述三種類型。然而在針對多邊形柱狀模型的多邊形頂面進行四邊形分區時，只希望得到凸四邊形，而另外兩種則是不希望出現的。為此，在進行四邊形區域質量計算時，對于所不希望出現的四邊形類型，將通過設置相應的懲戒系數來作為其質量，以避免該類型四邊形的出現。因此，有關各種四邊形區域質量的計算方法，概括為

式中，Q為第個四邊形區域的質量；、為設置的懲戒系數，且＜＜0。

對于多四邊形區域的綜合質量，本文提出取各四邊形區域的平均質量作為其綜合質量，即

式中，av為四邊形區域的平均質量；為四邊形區域的個數。

4 多邊形頂面的四邊形分區優化方法

如上所述，在采用結構化網格劃分法對交流牽引電機轉子導條等多邊形柱狀模型進行網格劃分前，首先需對該模型的多邊形頂面進行四邊形分區。下面首先介紹其四邊形的分區方式，再闡述對相應分區方式進行優化的方法。

4.1 多邊形頂面的四邊形分區方式

為將多邊形頂面劃分為若干個四邊形區域，本文提出一種基于內置四邊形的區域劃分法。其基本原理是：在多邊形頂面內任意添加一個四邊形，并由該四邊形各頂點分別向頂面各頂點或頂面各邊上所選取的點引線，由此將多邊形頂面劃分成若干個四邊形區域。其中，所添加的四邊形稱為內置四邊形，為方便分析，將內置四邊形各頂點稱為內點，頂面多邊形各頂點稱為角點，而在頂面多邊形各邊上所選取的點稱為邊點。

下面首先介紹邊點數的確定方法，再闡述四邊形分區方式的具體實現方法。

4.1.1 邊點數確定方法

在將多邊形頂面劃分為若干個四邊形區域過程中，為使所獲得的各四邊形區域尺寸基本均衡，本文提出按多邊形頂面各邊邊長來確定其邊點數的方法。其基本原理是：以多邊形頂面最短邊為基準，并規定最短邊不設邊點，再將其他各邊邊長分別與之比較，其比值在大于1后按每增加50%，則在該邊上增加1個邊點的方法來確定其邊點數，且規定其上限為3個。

根據上述方法，則如果某邊邊長超過最短邊50%而不足100%時，將在該邊上設一個邊點；同樣，如果某邊邊長超過最短邊100%而不足150%時，則在該邊上設兩個邊點；而如果某邊邊長超過最短邊150%及以上時，則在該邊上設3個邊點，由此可確定多邊形頂面各邊上的邊點數。

4.1.2 多邊形頂面的四邊形分區方法

針對多邊形頂面進行四邊形分區，多邊形頂面的四邊形分區流程如圖5所示。

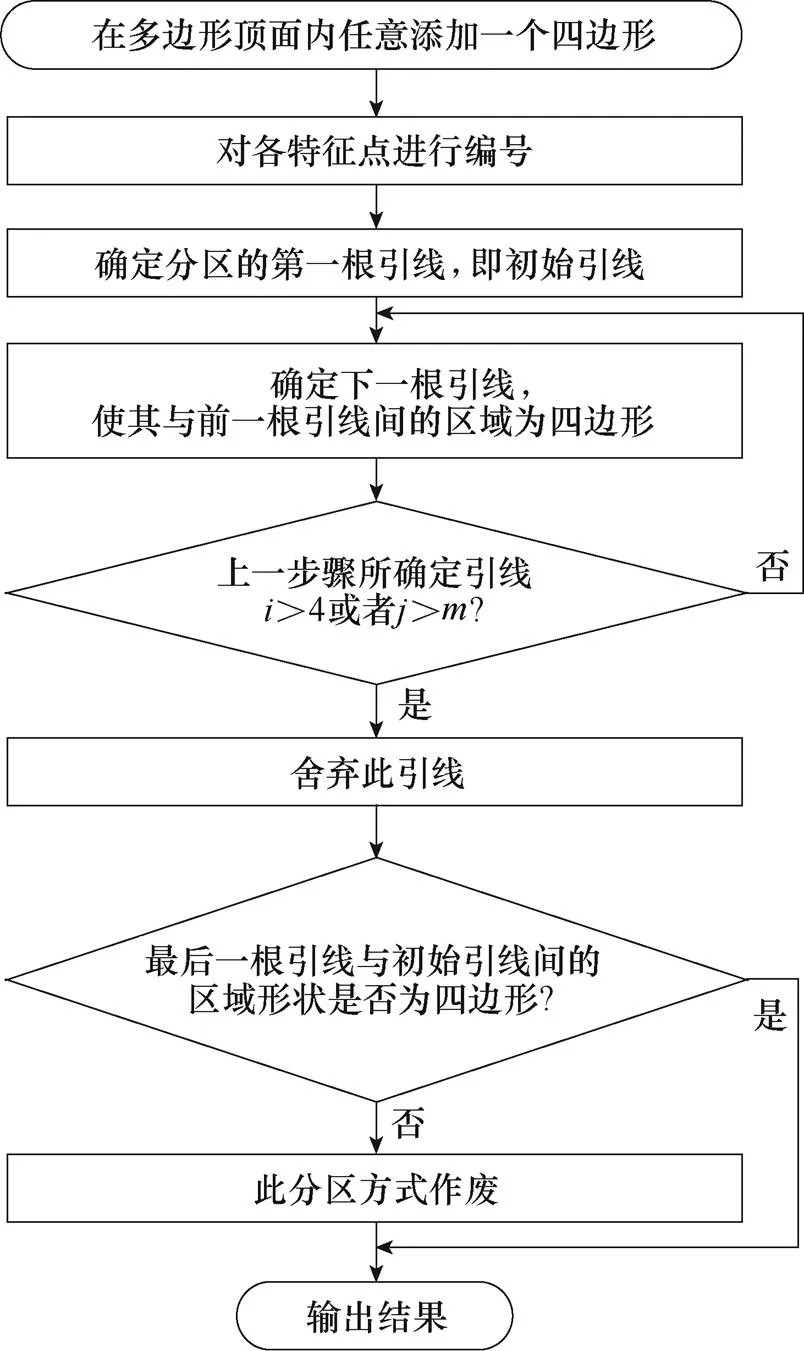
圖5 多邊形頂面的四邊形分區流程

具體介紹如下：

（1）在多邊形頂面內任意添加一個四邊形。

（2）對各特征點進行編號，特征點包括內點、角點和邊點，其編號規則如下：

設內點用N（=1, 2, 3, 4）表示，并設多邊形頂面有個角點，各角點用J（=1, 2,…,）表示，同時規定以多邊形頂面最短邊兩側角點中任取一個為1，并由1開始沿其另一側角點方向依次對其他各角點編號；另外，頂面各邊上的邊點用B（=1, 2,…,；=1, 2, 3）表示，其下標表示以第個角點為起點所對應的第條邊，表示該邊上的第個邊點。

（3）確定分區的第一根引線，即初始引線。為方便說明，規定初始引線為1與1間連線。

（4）確定下一根引線，使此引線與其前一根引線之間的區域為四邊形。

前一根引線包括內點與角點間連線與內點與邊點間連線兩種情況，引線確定示意圖如圖6所示。

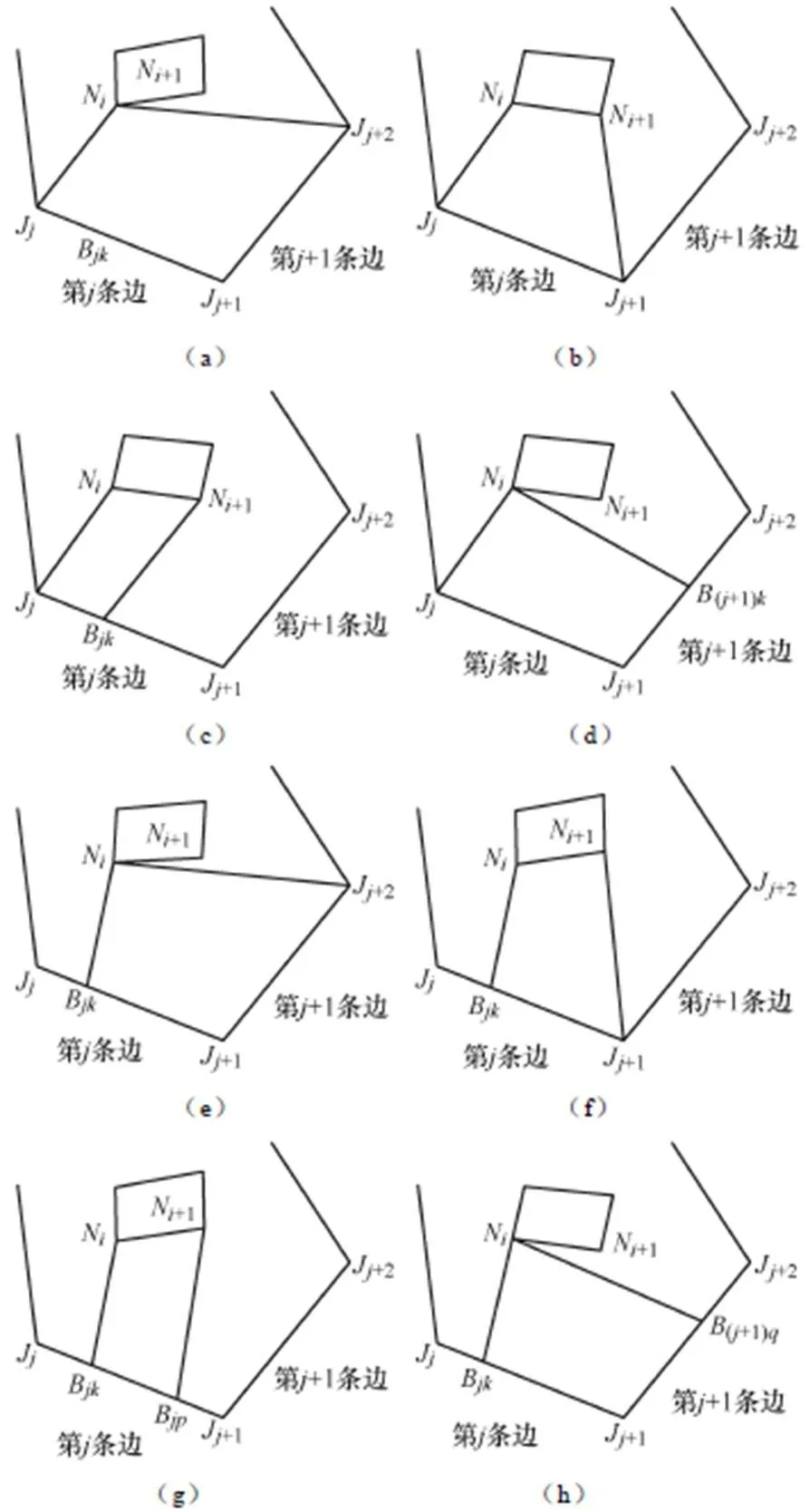
圖6 引線確定示意圖

圖6a～圖6d表示當前引線為內點N與角點J間連線的情況，下一根引線可取N與J2間連線或N1與J1間連線，詳見圖6a與圖6b；同時如果第條邊或第+1條邊上有邊點，則下一根引線還可取N1與B間連線或N與(j+1)k間連線，詳見圖6c與圖6d，其中，B與(j+1)k分別表示相應邊上第個邊點。

圖6e～圖6h表示當前引線為內點N與邊點B間連線的情況，下一根引線可取N與J2間連線或N1與J1間連線，詳見圖6e與6f；同時如果第條邊的邊點總數大于當前引線對應邊點B的序號時，則下一根引線還可取N1與B間連線，詳見圖6g，其中：＜≤；此外，如果第+1條邊上有邊點，則下一根引線還可取N與(j+1)q間連線，詳見圖6h，(j+1)q表示第+1條邊上第個邊點。

（5）對上述確定的引線進行判斷，若出現了＞4或者＞的情況，則此引線必與初始引線相交，因此需要舍棄此引線，否則返回步驟（4）。

（6）判斷每種分區方式最后一根引線與第一根引線間的區域形狀是否為四邊形，若為四邊形，則輸出該分區方式，否則此分區方式作廢。

4.2 四邊形分區方式優化方法

對于上述所確定的四邊形分區方式，因各角點坐標是固定的，而各內點和邊點坐標則可進行優化調節；因此以各內點和邊點坐標為優化對象，以各四邊形區域的綜合質量為優化目標，采用果蠅算法對其進行優化，得到該分區方式下最大綜合質量所對應的各內點和邊點坐標，從而獲得多邊形頂面所對應的最佳四邊形分區方式。相應的優化設計流程如圖7所示。

具體介紹如下：

（1）初始化算法參數，包括果蠅飛行半徑、果蠅種群規模Popsize、最大迭代次數Maxgen，并設果蠅個體味道濃度極大值smell_best的初始值為0。

（2）隨機賦予果蠅個體位置坐標，即內點、邊點坐標，使初代果蠅個體坐標分布在頂面邊線和頂面內部的隨機位置，使非初代果蠅個體坐標分布在以保留的內點、邊點為圓心，以果蠅飛行半徑為半徑的圓內隨機位置。

（3）計算果蠅個體味道濃度值，即各四邊形區域的綜合質量av，具體步驟為：①首先根據各四邊形區域的頂點坐標及式（17）～式（19），計算得到混合積、、，再根據所得混合積判定出各四邊形區域的形狀；②根據各四邊形區域形狀并結合式（20）及式（12）～式（16），計算得到各四邊形區域的質量；③再根據所得各四邊形區域質量及式（21），即可計算出各四邊形區域的平均質量av，并以該平均質量作為果蠅個體的味道濃度值。

（4）比較果蠅個體味道濃度值av，獲得此次迭代中果蠅個體味道濃度值的最大值max_smell。

（5）判斷此次迭代中果蠅個體味道濃度最大值max_smell是否優于所保留的果蠅個體味道濃度極大值smell_best；若是，則將max_smell值取代smell_best值作為新的果蠅個體味道濃度極大值，并保留其對應的果蠅個體位置坐標；否則，執行步驟（6）。

（6）進入迭代尋優，判斷迭代次數是否達到最大迭代次數Maxgen；若是，則進入步驟（7）；否則，返回步驟（2）。

（7）輸出結果，即輸出果蠅個體味道濃度極大值smell_best所對應的各內點、邊點坐標。

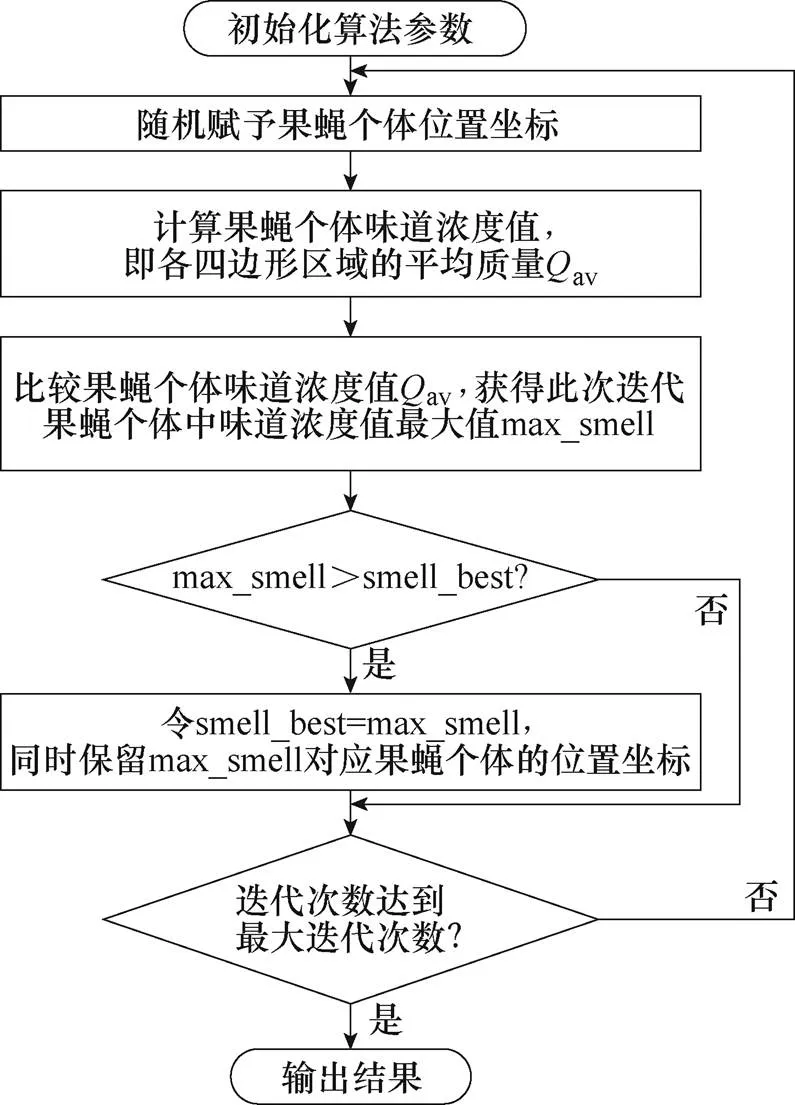
圖7 四邊形分區優化設計流程

5 交流牽引電機溫度場分析

為驗證上述多邊形柱狀模型結構化網格優化劃分方法的效果，以Y100L2-4型交流牽引電機為例，采用有限元法對其進行溫度場分析，其主要結構參數見表1，轉子導條頂面示意圖如圖8所示。

在針對交流牽引電機有限元法模型進行網格劃分時，其轉子導條采用結構化網格優化劃分方法，其余部位則采用傳統網格劃分法；并設置轉子導條優化劃分的相關參數為：果蠅飛行半徑取0.2，果蠅個體數設為2 000，迭代次數取300。所得轉子導條結構化網格優化劃分結果如圖9所示，對應的交流牽引電機三維溫度場分布如圖10所示。

表1 Y100L2-4型電機主要結構參數

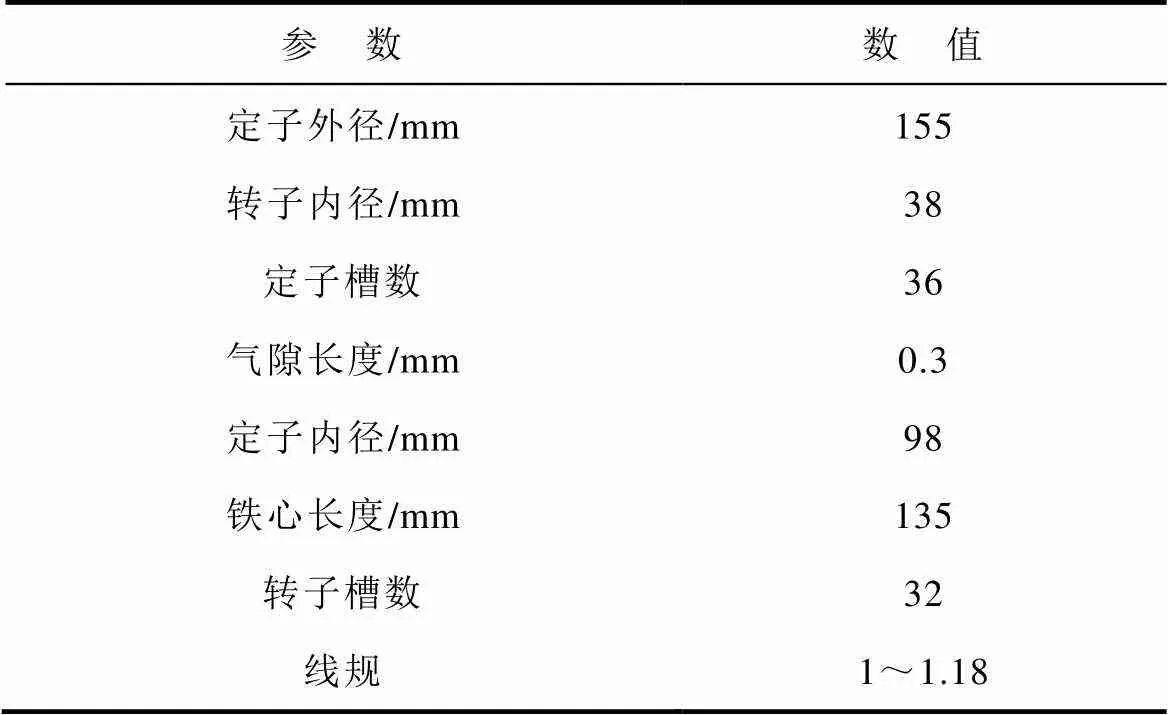
Tab.1 Main structural parameters of Y100L2-4 motor

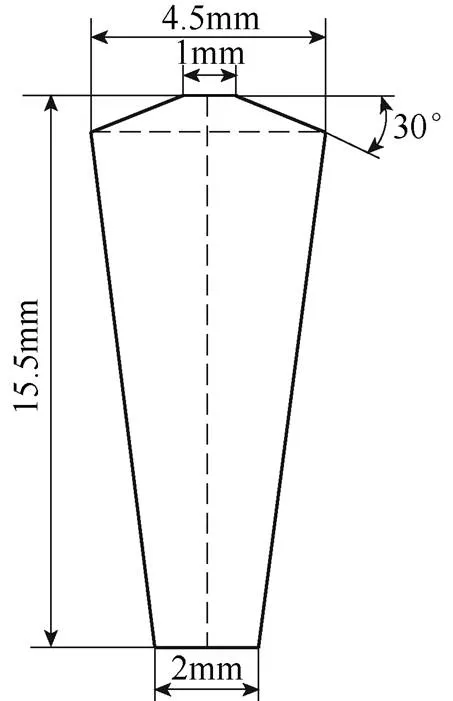
圖8 轉子導條頂面示意圖

圖9 轉子導條結構化網格優化劃分結果

同時，為便于說明本文提出的結構化網格優化劃分方法的效果，再針對上述轉子導條采用傳統結構化網格劃分，其余部位網格劃分方法不變，則得到相應的轉子導條網格劃分結果及電機三維溫度場分布分別如圖11和圖12所示。

圖10 轉子導條結構化網格優化劃分對應的電機溫度場分析仿真

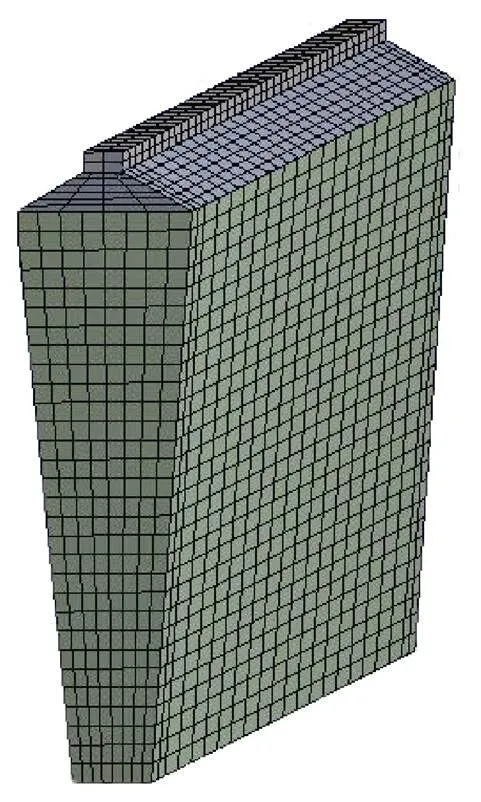
圖11 轉子導條傳統結構化網格劃分結果

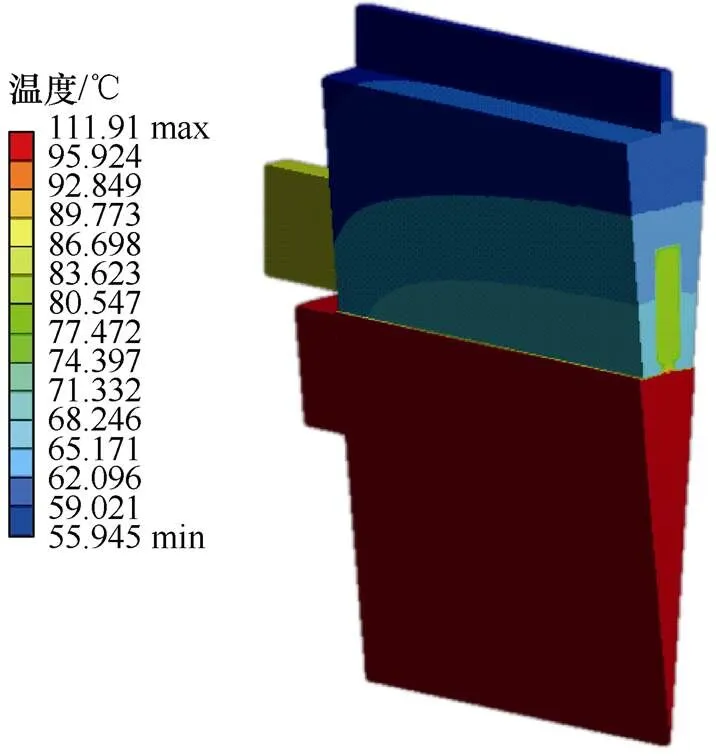
圖12 傳統結構化網格劃分后電機溫度場分析仿真

對應于上述兩種網格劃分方法所得轉子導條網格劃分質量見表2，而對應電機溫度場分析所得各主要部位的溫度則見表3。

表2 兩種網格劃分法對應的轉子導條網格劃分質量

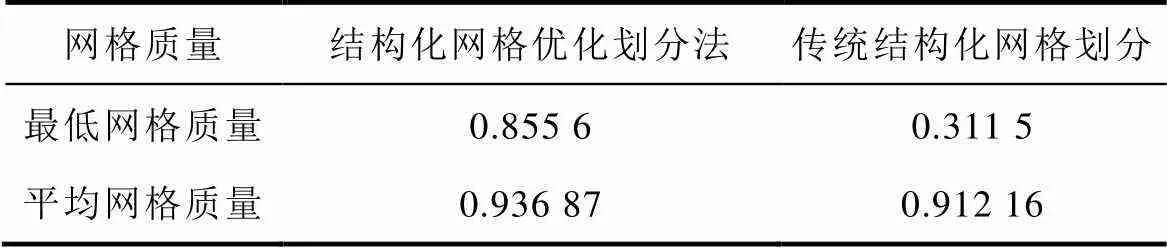
Tab.2 The meshing quality of rotor guide bar corresponding to two meshing methods

表3 電機主要部位溫度

Tab.3 Temperature of main parts of motor （單位: ℃）

由表2可見，相較于傳統結構化網格劃分方 法，本文提出的結構化網格優化劃法所得網格的平均質量雖然只提高了0.024 71，但最低網格質量卻由0.311 5提高到0.855 6，相當于提高了1.74倍。由于溫度場分析誤差主要受低質量網格的影響，因而低質量網格的質量得到提升后，將會顯著改善分析結果的準確性。同時由表3可見，采用結構化網格優化劃法所得各主要部位的溫度場分析結果，相對于傳統結構化網格劃分法，其偏差均達到了0.6℃以上，說明兩種方法的效果存在較大差異。

6 實驗分析

為進一步驗證本文提出的多邊形柱狀模型結構化網格優化劃分方法的效果，構建交流牽引電機實驗裝置進行驗證，如圖13所示。該實驗裝置選用Y100L2-4型交流牽引電機，其主要參數見表4，除此之外還有控制器、磁粉制動器、張力控制器、溫度傳感器、溫度顯示器、轉矩轉速測量儀等。其中，定子繞組端部、定子鐵心溫度采用溫度傳感器檢測，而電機機殼溫度則采用紅外測溫儀測量。

實驗時電機以額定工況運行，當電機各部分溫度顯示穩定后，分別讀取相應的溫度值，見表5。其中，電機機殼溫度因采用紅外測溫儀測量，存在一定的誤差，故對其進行了相應的補償[23]。

對照表3與表5，得到在電機溫度場分析中兩種網格劃分法所得電機各主要部件溫度相對于其實測溫度的相對誤差，見表6。可見，采用結構化網格優化劃分方法，使電機各主要部件溫度相對于其實測溫度的偏差有了明顯的下降，從而驗證了該方法的有效性。

圖13 電機溫升實驗平臺

表4 電機主要參數

Tab.4 Main parameters of motor

表5 電機溫度實驗值

Tab.5 Experimental value of motor temperature

表6 仿真結果相對實驗結果的偏差比較

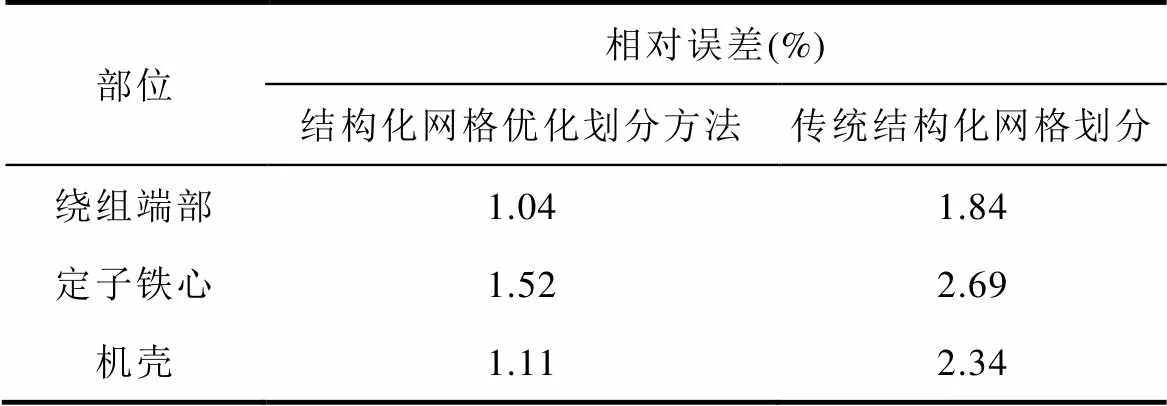
Tab.6 Comparison of deviation between simulation results and experimental results

7 結論

針對交流牽引電機轉子導條等多邊形柱狀熱分析模型結構化網格劃分質量不高的問題，提出一種結構化網格優化劃分方法。建立了交流牽引電機熱分析的求解域模型，確定了交流牽引電機多邊形柱狀模型的四邊形區域質量計算方法，提出一種基于內置四邊形的多邊形柱狀模型四邊形區域劃分方法，并采用果蠅算法對各分區方式的綜合質量進行優化以獲得相應的最佳分區方式，最后通過仿真和實驗對所提出的網格劃分方法進行驗證，同時與傳統結構化網格劃分方法進行對比分析。結果表明，本文所提出的結構化網格優化劃分法較傳統結構化網格劃分法顯著提高了交流牽引電機多邊形柱狀模型的網格劃分質量，由此有效地提高了交流電機熱分析的準確性，對于指導交流牽引電機的優化設計具有重要意義。

[1] Shafighy M, Khoo S, Kouzani A Z. Modelling and simulation of regeneration in AC traction propulsion system of electrified railway[J]. IET Electrical Systems in Transportation, 2015, 5(4): 145-155.

[2] Jurkovic S, Rahman K M, Morgante J C, et al. Induction machine design and analysis for general motors e-assist electrification technology[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 631-639.

[3] 佟文明, 孫靜陽, 舒圣浪. 不同數值方法在自扇冷永磁同步電機三維熱分析中的應用[J]. 電工技術學報, 2017, 32(1): 151-159.

Tong Wenming, Sun Jingyang, Shu Shenglang. Appli- cation of different numerical methods in three dimensional thermal analysis of self-fan-cooled permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(1): 151-159.

[4] 上官璇峰, 蔣思遠, 周敬樂, 等. 雙轉子雙鼠籠永磁感應電機三維全域溫度場分析[J]. 電機與控制學報, 2018, 22(11): 58-66.

Shangguan Xuanfeng, Jiang Siyuan, Zhou Jingle, et al. Analysis on 3-D temperature field of dual-rotor permanent magnet induction motor with double squirrel cage[J]. Electric Machines and Control, 2018, 22(11): 58-66.

[5] Cai Xiuhua, Cheng Ming, Zhu Sa, et al. Thermal modeling of flux-switching permanent-magnet machines considering anisotropic conductivity and thermal contact resistance[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3355-3365.

[6] 陳劍, 劉春明, 王茂海, 等. 廣義有限差分法在靜態電磁場計算中的應用[J]. 電工技術學報, 2018, 33(7): 1579-1587.

Chen Jian, Liu Chunming, Wang Maohai, et al. Application of the generalized finite difference method to static electromagnetic problems[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1579- 1587.

[7] 劉小梅. 封閉式小型異步電機的溫度場研究[D]. 焦作: 河南理工大學, 2014.

[8] Zhang Yujiao, Ruan Jiangjun, Huang Tao, et al. Calculation of temperature rise in air-cooled induction motors through 3-D coupled electromagnetic fluid- dynamical and thermal finite-element analysis[J]. IEEE Transactions on Magnetics, 2012, 48(2): 1047- 1050.

[9] 石晶. 汽車發電機溫度場有限元分析與計算[J]. 微電機, 2015, 48(5): 41-46.

Shi Jing. Finite element analysis and calculation of temperature field of automobile generator[J]. Micro- motors, 2015, 48(5): 41-46.

[10] 謝穎, 王澤, 單雪婷. 基于多場量的籠型感應電機三維瞬態磁熱固耦合計算分析[J]. 中國電機工程學報, 2016, 36(11): 3076-3084.

Xie Ying, Wang Ze, Shan Xueting. Calculation and analysis of three-dimensional transient magneto thermo mechanical coupling of cage induction motor based on multi field[J]. Proceedings of the CSEE, 2016, 36(11): 3076-3084.

[11] 謝穎, 黎志偉, 郭金鵬. 電動汽車用高功率密度感應電機的設計與研究[J]. 電機與控制學報, 2020, 24(2): 46-54.

Xie Ying, Li Zhiwei, Guo Jinpeng. Design and research on high power density induction motor in electric vehicle[J]. Electric Machines and Control, 2020, 24(2): 46-54.

[12] 邰永. 感應電機全域三維瞬態溫度場分析[J]. 中國電機工程學報, 2010, 30(30): 114-120.

Tai Yong. Three dimensional transient temperature field analysis of induction motor[J]. Proceedings of the CSEE, 2010, 30(30): 114-120.

[13] 劉剛, 孫立鵬, 王雪剛, 等. 正弦及諧波激勵下的鐵心損耗計算方法改進及仿真應用[J]. 電工技術學報, 2018, 33(21): 4909-4918.

Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improve- ment of core loss calculation method and simulation application under sinusoidal and harmonic excita- tions[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.

[14] 劉偉亮. 電動車用感應電機損耗及熱系統的研究[D]. 哈爾濱: 哈爾濱工業大學, 2006.

[15] 吳柏禧, 萬珍平, 張昆, 等. 考慮溫度場和流場的永磁同步電機折返型冷卻水道設計[J]. 電工技術學報, 2019, 34(11): 2306-2314.

Wu Boxi, Wan Zhenping, Zhang Kun, et al. Design of reentrant cooling channel in permanent magnet synchronous motor considering temperature field and flow field[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2306-2314.

[16] Li Weili, Cao Junci, Zhang Xiaochen. Electrothermal analysis of induction motor with compound cage rotor used for PHEV[J]. IEEE Transactions on Industrial Electronics, 2010, 57(2): 660-668.

[17] 李偉力. 感應電動機定轉子全域溫度場數值計算及相關因素敏感性分析[J]. 中國電機工程學報, 2007, 27(24): 85-91.

Li Weili. Numerical calculation of temperature field of stator and rotor of induction motor and sensitivity analysis of related factors[J]. Proceedings of the CSEE, 2007, 27(24): 85-91.

[18] Hatziathanassiou V, Xypteras J, Archontoulakis G. Electrical-thermal coupled calculation of an asy- nchronous machine[J]. Archiv für Elektrotechnik, 1994, 77(2): 117-122.

[19] 吳勝男, 李文杰, 安忠良, 等. 變速恒壓混合勵磁風力發電機的熱分析[J]. 電工技術學報, 2019, 34(9): 1857-1864.

Wu Shengnan, Li Wenjie, An Zhongliang, et al. Thermal analysis of variable-speed constant-voltage hybrid excited wind generators[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1857- 1864.

[20] 王小飛, 代穎, 羅建. 基于流固耦合的車用永磁同步電機水道設計與溫度場分析[J]. 電工技術學報, 2019, 34(增刊1): 22-29.

Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.

[21] 李海峰, 吳冀川, 劉建波. 有限元網格剖分與網格質量判定指標[J]. 中國機械工程, 2012, 23(3): 368- 377.

Li Haifeng, Wu Jichuan, Liu Jianbo. Finite element mesh generation and mesh quality criteria[J]. China Mechanical Engineering, 2012, 23(3): 368-377.

[22] 張青春. 基于四叉樹的復雜邊界四邊形網格自適應生成方法研究[D]. 沈陽: 東北大學, 2012.

[23] 廖盼盼, 張佳民. 紅外測溫精度的影響因素及補償方法的研究[J]. 紅外技術, 2017, 39(2): 173-177.

Liao Panpan, Zhang Jiamin. Research on the influence factors and compensation methods of infrared tem- perature measurement accuracy[J]. Infrared Tech- nology, 2017, 39(2): 173-177.

A Structured Mesh Optimization Method for Polygonal Columnar Thermal Analysis Model Based on Drosophila Algorithm

1,21,21,223

（1. National-Local Joint Engineering Laboratory of Marine Mineral Resources Exploration Equipment and Safety Technology Hunan University of Science and Technology Xiangtan 411201 China 2. College of Information and Electrical Engineering Hunan University of Science and Technology Xiangtan 411201 China 3. Xiangtan Electric Manufacturing Co. Ltd Xiangtan 411101 China）

The structured mesh generation in polygonal cylindrical thermal analysis model has low quality, such as rotor guide bar of AC traction motor. Therefore, an optimized method of structured mesh generation is proposed. In this paper, the solution domain model of AC traction motor thermal analysis is established, and the quadrilateral region mass calculation method of AC traction motor polygonal cylinder model is determined. Then, a quadrilateral region division method of polygonal cylinder model based on built-in quadrilateral is proposed, and the fruit fly optimization algorithm (FOA) is used to optimize the comprehensive quality of each partition mode to obtain the corresponding optimal partition mode. Through the finite element method, the proposed method is compared with the traditional structured mesh generation method, and its effect is verified. Finally, the above analysis is further verified by experiments. The results show that compared with the traditional structured mesh generation method, the method proposed in this paper greatly improves the mesh generation of the polygon cylinder model of AC traction motor, thereby improving the accuracy of thermal analysis of AC traction motor, which has good application value.

AC traction motor, polygonal columnar thermal analysis model, structured grid, optimized partition method, fruit fly optimization algorithm (FOA)

TM343+.2

10.19595/j.cnki.1000-6753.tces.200353

長株潭國家自主創新示范區專項資助項目（2017XK2303）。

2020-04-09

2020-06-16

郭宇軒 男，1994年生，碩士研究生，研究方向為電力電子與電力傳動。E-mail: 453877764@qq.com

張小平 男，1966年生，博士，教授，碩士生導師，研究方向為電力電子與電力傳動、智能控制等。E-mail: zxp836@163.com（通信作者）

（編輯 崔文靜）