三維TTI介質彈性波相、群速度的近似配方表征法

孫上饒 梁 鍇 印興耀 曹丹平 李 坤

(中國石油大學(華東)地球科學與技術學院，山東青島，266580)

0 引言

橫向各向同性(TI)介質廣泛存在于地下，如周期性薄互層、裂隙定向排列地層等。實際地下TI介質對稱軸的取向往往沿空間任意方向分布，稱為任意空間取向TI介質(ATI介質)[1]。當TI介質對稱軸與垂直方向存在一定夾角，但方位限定在入射平面內時就稱為TTI(Tilted Transversly Isotropical)介質。對于傾斜地層，TTI模型相比于VTI和HTI模型更符合實際地層特征。

各向異性介質的相速度是相角的函數，群速度是相速度的函數，二者均是描述波傳播特性的重要參數。通過求解Christoffel方程可以得到TTI介質相速度的精確表達式[2-5]。TTI介質qP波、qSV波相速度和群速度精確表達式各包含四個獨立彈性參數。Alkhalifah等[6-7]的研究表明，這四個參數中的三個參數的組合即可較高精度地描述qP波和qSV波的傳播特征。然而，由于TTI介質彈性波相速度的表達式過于復雜，難以用于實際地震資料處理，以較為精確的近似表達式替代精確表達式以進行速度分析就顯得尤為重要，為此提出了TI介質相速度和群速度的多種近似方法[5，8-19]。Fowler[12]對VTI介質相、群速度十余種不同的近似式進行了系統地比較和討論，指出對于P波相速度，大多數近似方法有著足夠精度以滿足實際資料處理的需求；而對于SV波，由于其速度小于P波速度，所以SV波近似中的相對誤差往往大于P波，并且由于VTI介質中的相速度具有顯式的解析解，與相應的群速度相比，相速度更容易近似。Fomel[14]對Dellinger等[20]的近似方法進行了詳細對比分析，提出用三個參數代替精確表達式中的四個參數。Aleixo等[21]和Golikov等[22]比較了幾種群速度近似的精度。中國也有多位學者對TI介質體波速度特征開展了深入研究，并應用于地震波正演和偏移等[23-28]。吳國忱等[29-30]推導了三維空間TTI介質彈性波相速度的精確表達式及其弱各向異性近似；李芳等[31]在計算各向異性介質速度的過程中考慮了剪切波的奇點特性，提出了任意各向異性介質彈性波相速度和群速度計算方法；梁鍇等[32]推導了傾斜橢球各向異性介質的相速度和群速度表達式，并分析了Thomsen各向異性參數對相、群速度傳播特征的影響；谷一鵬等[33]提出了VTI介質彈性波相速度的擴展各向異性線性近似，該方法可以通過控制精確相速度曲線與擴展各向異性線性近似曲線的切點，使該近似在不同程度的各向異性介質中取得較高的精度。由于弱各向異性近似假設并不能很好地適應頁巖等中強各向異性介質，因此梁鍇等[34]基于近似配方法的思想，推導了二維TTI介質qP波和qSV波相速度一般性近似，數值示例表明該近似相速度可適用于中強各向異性介質。

本文以基于近似配方法的TTI介質彈性波二維相速度近似式[34]為基礎，在原有近似中引入方位角，推導了三維相速度的近似式，進而根據Berryman公式[35]導出了基于近似配方法的群速度近似式。利用兩組介質模型參數對相、群速度精確值和近似值進行了數值計算，探討了該近似相、群速度在不同各向異性參數組合下的相對誤差，并進行了適用性分析。

1 TTI介質精確和近似彈性波相、群速度

1.1 TTI介質彈性波相速度的精確表征

在進行地震波正演模擬時往往需要將各向異性介質的剛度矩陣從本構坐標系變換到觀測坐標系。基于坐標變換方法，定義TTI介質本構坐標系O(x′，y′，z′)和觀測坐標系O(x，y，z)如圖1所示，其中θ0為TTI介質對稱軸Oz′與觀測坐標系z軸的夾角，極角θ為傳播矢量k與z軸的夾角，方位角φ為傳播矢量k在Ω平面上的投影與x軸的夾角。利用Bond變換[36]可以將TI介質本構坐標系下的剛度矩陣轉變為觀測坐標系下的剛度矩陣。

將平面波解代入TTI介質波動方程，得到TTI介質的Kelvin-Christoffel方程為

(1)

式中：Γij(i，j=1，2，3)為Christoffel矩陣元素；px、py、pz為偏振方向的三個分量。令式(1)系數矩陣行列式為零，可求解得到TTI介質的qP波、qSV波和SH波的相速度精確表達式

(2)

式中

(3)

(4)

其中：vP0和vS0分別為qP波和qSV波沿TTI介質對稱軸方向傳播的相速度；ε為度量qP波各向異性強度的參數；γ是度量橫波分裂強度的參數，當γ=0時，SH波無各向異性；δ為表征TTI介質對稱軸方向qP波相速度曲線凹凸性的參數。

將Thomsen參數表征的VTI介質剛度矩陣元素(式(4))代入TTI介質彈性波相速度的精確表達式(式(2))中，可得由Thomsen參數表征的TTI介質彈性波三維相速度表達式

(5)

式中

(6)

TTI介質彈性波的相速度表達式較為復雜，常見的弱各向異性近似、橢圓各向異性近似等可以在一定范圍內對精確式進行簡化，但在中強各向異性介質中，這些近似相速度誤差較大，進而影響速度分析以及偏移處理的精度。

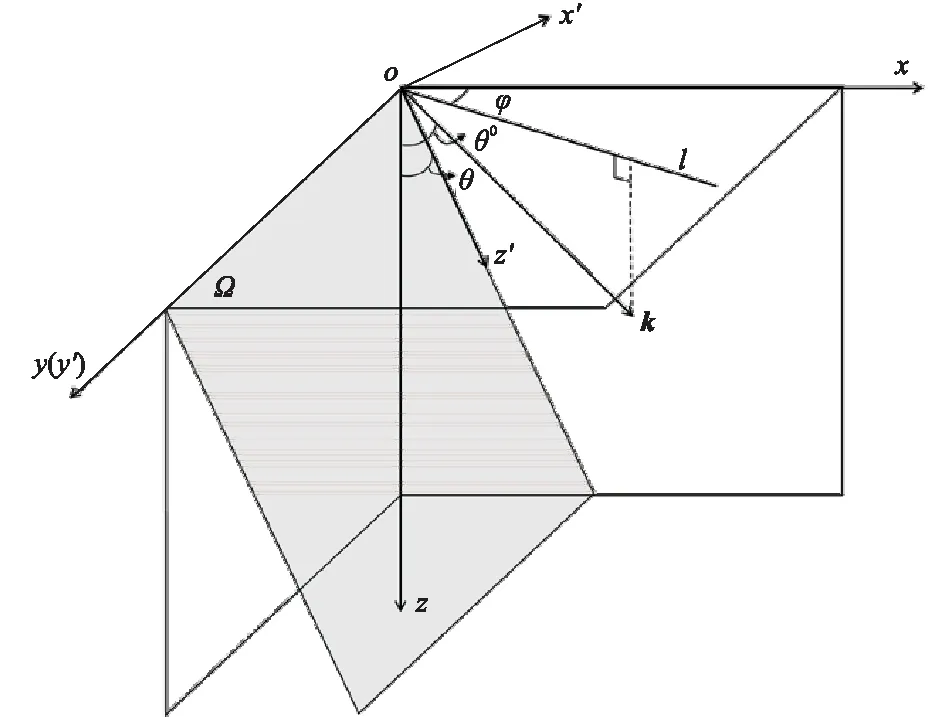
圖1 TTI介質本構坐標系與觀測坐標系的關系示意圖

1.2 TTI介質彈性波相速度的近似表征

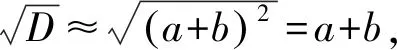
從TTI介質彈性波相速度精確表達式(式(5))出發，提取P波和SV波精確相速度存在的共同項

(7)

令

(8)

(9)

則D可以表示為

D=a2+2ab+b2+

[2ε(E2+F2)+(δ-ε)(E2+F2)G2]

(10)

采用如下近似

[2ε(E2+F2)+(δ-ε)(E2+F2)G2]

(11)

則有

(12)

將上式代入相速度精確表達式(式(5))就可得到基于近似配方法的TTI介質qP波和qSV波三維相速度近似式

(13)

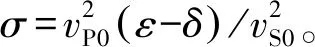
(14)

上式與橢圓各向異性情況下精確相速度的形式完全相同[32]。

1.3 TTI介質彈性波群速度的近似表征

各向異性介質地震波群速度決定了地震波能量傳播的速度和方向，在地震波旅行時的正演和反演中起著重要的作用。均勻各向異性介質中群速度是相速度的函數，群速度計算一般可以用Berryman公式[35]表示為

(15)

式中k=(kx，ky，kz)，為彈性波波矢量，其模k=ω/v，其中v為彈性波相速度、ω為角頻率。

根據前人推導TTI介質彈性波群速度的思想[40-41]，將相速度近似式(13)代入式(15)中，就可得到TTI介質彈性波群速度的近似表征。其中qP波群速度的近似表征為

(16)

式中

(17)

其中

(18)

qSV波群速度的近似表征為

(19)

式中

(20)

在橢圓各向異性情況下，式(17)可退化為

(21)

式(20)中相速度對極角和方位角的偏導數?vSVa/?θ和?vSVa/?φ為零。這樣，TTI介質橢圓各向異性情況下的近似群速度表達式就可等同于精確群速度表達式。

2 數值示例

本文推導的三維TTI介質qP波和qSV波相、群速度的近似表達式在形式上較精確表達式更為簡潔。選取Vernik等[42]給出的兩個頁巖模型(均為中強各向異性介質(表1))驗證本文基于近似配方法的TTI介質彈性波三維相、群速度近似表征的正確性。

2.1 相、群速度數值試算

基于本文近似配方法的三維TTI介質彈性波相、群速度近似表達式，分別計算模型Ⅰ和模型Ⅱ的相速度和群速度。圖2為模型Ⅰ和模型Ⅱ的三維近似qP波和qSV波相速度曲面，對應的xOz、yOz、xOy面的近似相速度曲線與精確相速度曲線的對比如圖3所示。利用相同的模型可以得到三維近似群速度曲面(圖4)及其近似的群速度曲線(圖5)。由圖2、圖4可見，近似和精確相、群速度在三維空間中的速度特征相似。由圖3、圖5可見本文的近似相、群速度表達式在中強各向異性情況下可以保持較高的精度。

由圖3可見，在沿TTI介質對稱軸方向(圖中黑色短線方向)以及垂直對稱軸方向傳播時，近似qP波和qSV波相速度與精確值的誤差最小，而在與對稱軸呈45°方向附近的誤差較大。由qP波近似相速度公式(式(13))可看出vS0對P波相速度的影響可以忽略不計，因而影響P波相速度的參數主要為vP0、ε和δ；而影響qSV波的參數則為vP0、vS0、ε和δ，用組合參數σ替代上述四個參數可以減少參數數量，便于描述qSV波的運動學特征；參數σ越大，相速度的近似值與精確值的差異也越大。圖5呈現的近似群速度特征與近似相速度特征相似，即在對稱軸方向及垂直對稱軸方向誤差最小，在45°方向附近誤差較大。

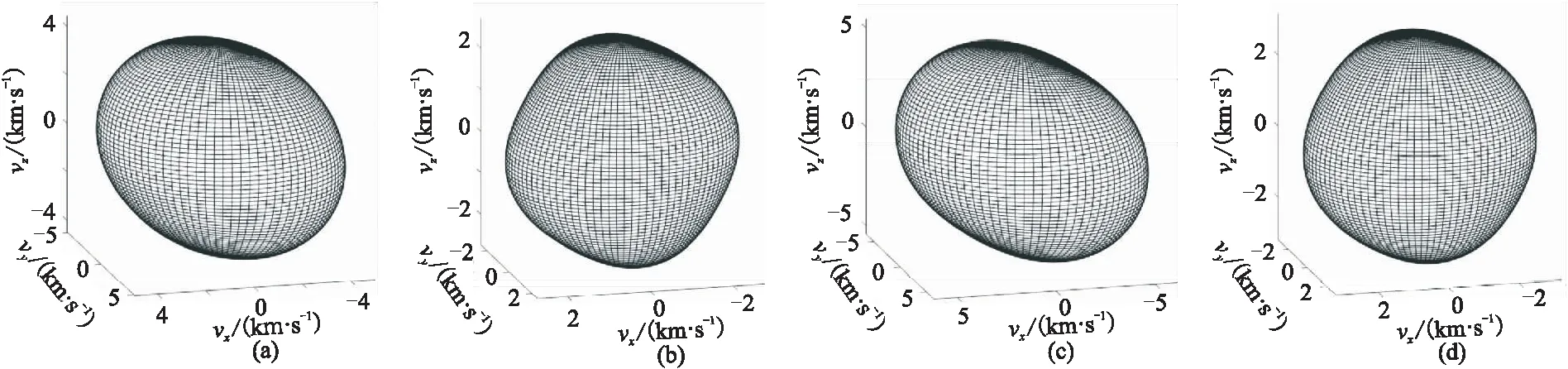
圖2 近似的三維TTI介質相速度曲面(a)模型Ⅰ，qP波； (b)模型Ⅰ，qSV波； (c)模型Ⅱ，qP波； (d)模型Ⅱ，qSV波

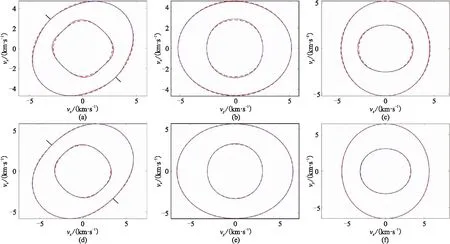
圖3 近似(藍色虛線)和精確(紅色實線)的三維TTI介質相速度曲線對比(a)模型Ⅰ，xOz面； (b)模型Ⅰ，yOz面； (c)模型Ⅰ，xOy面； (d)模型Ⅱ，xOz面； (e)模型Ⅱ，yOz面； (f)模型Ⅱ，xOy面

圖4 近似的三維TTI介質群速度曲面(a)模型Ⅰ，qP波； (b)模型Ⅰ，qSV波； (c)模型Ⅱ，qP波； (d)模型Ⅱ，qSV波

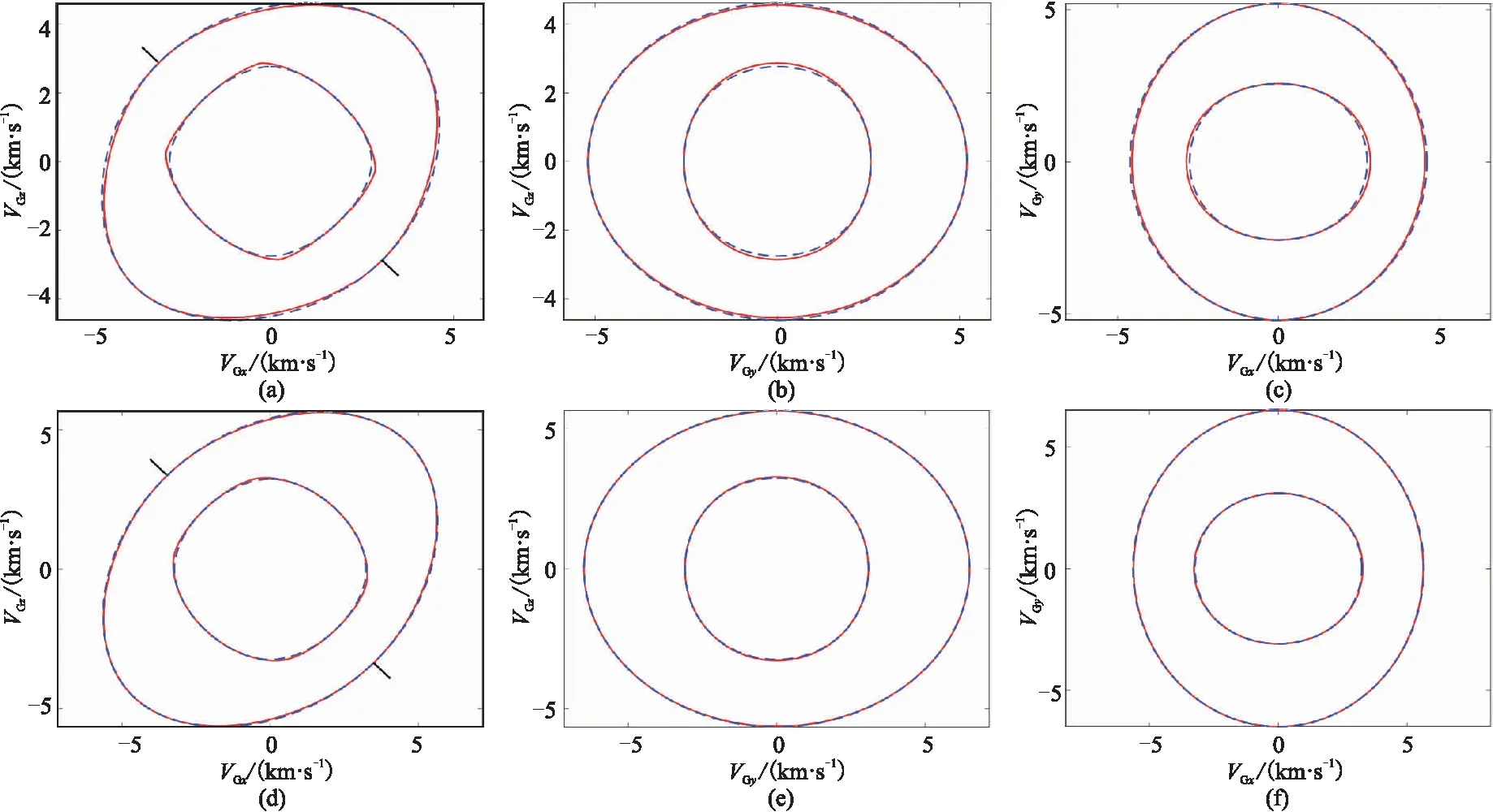
圖5 近似(藍色虛線)和精確(紅色實線)的三維TTI介質群速度曲線對比(a)模型Ⅰ，xOz面； (b)模型Ⅰ，yOz面； (c)模型Ⅰ，xOy面； (d)模型Ⅱ，xOz面； (e)模型Ⅱ，yOz面； (f)模型Ⅱ，xOy面

2.2 相對誤差分析

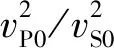
2.3 適用性分析

研究表明，沉積地層中ε取值范圍從中等各向異性地層的0.1～0.3到壓實頁巖地層的0.3～0.5，甚至更高[5，43]。為了方便討論本文的相、群速度近似公式對不同程度各向異性介質的適用性，給定軸向縱、橫波速度分別為vP0=4.19km/s、vS0=2.57km/s，θ0=45°，選取[0，0.8]內的ε、δ參數組合，對近似計算的相速度和群速度進行相對誤差分析，其最大相對誤差等值線如圖8所示，可見大部分各向異性參數組合對應的qP波相、群速度的相對誤差小于qSV波。在圖中對角線處，ε=δ，表示橢圓各向異性，最大相對誤差均為零，與理論相符。隨著參數|ε-δ|的增大，近似的相、群速度的最大相對誤差也越大。對比圖8a和圖8b可知，在δ遠大于ε的較為極端情況下，組合參數σ值更大，導致qSV波相、群速度相對誤差遠大于qP波。

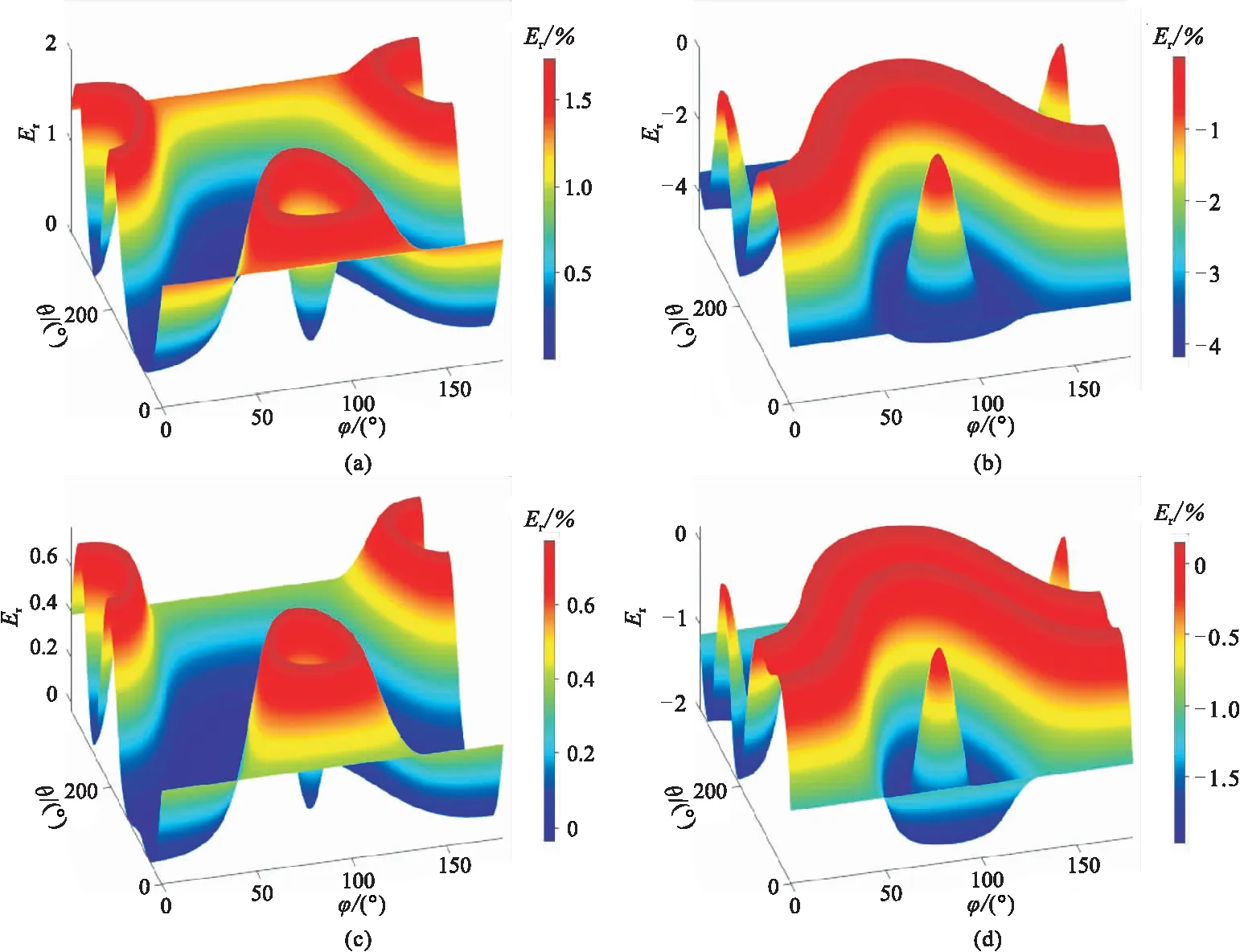
圖6 本文近似計算的TTI介質三維相速度相對誤差曲面(a)模型Ⅰ，qP波； (b)模型Ⅰ，qSV波； (c)模型Ⅱ，qP波； (d)模型Ⅱ，qSV波

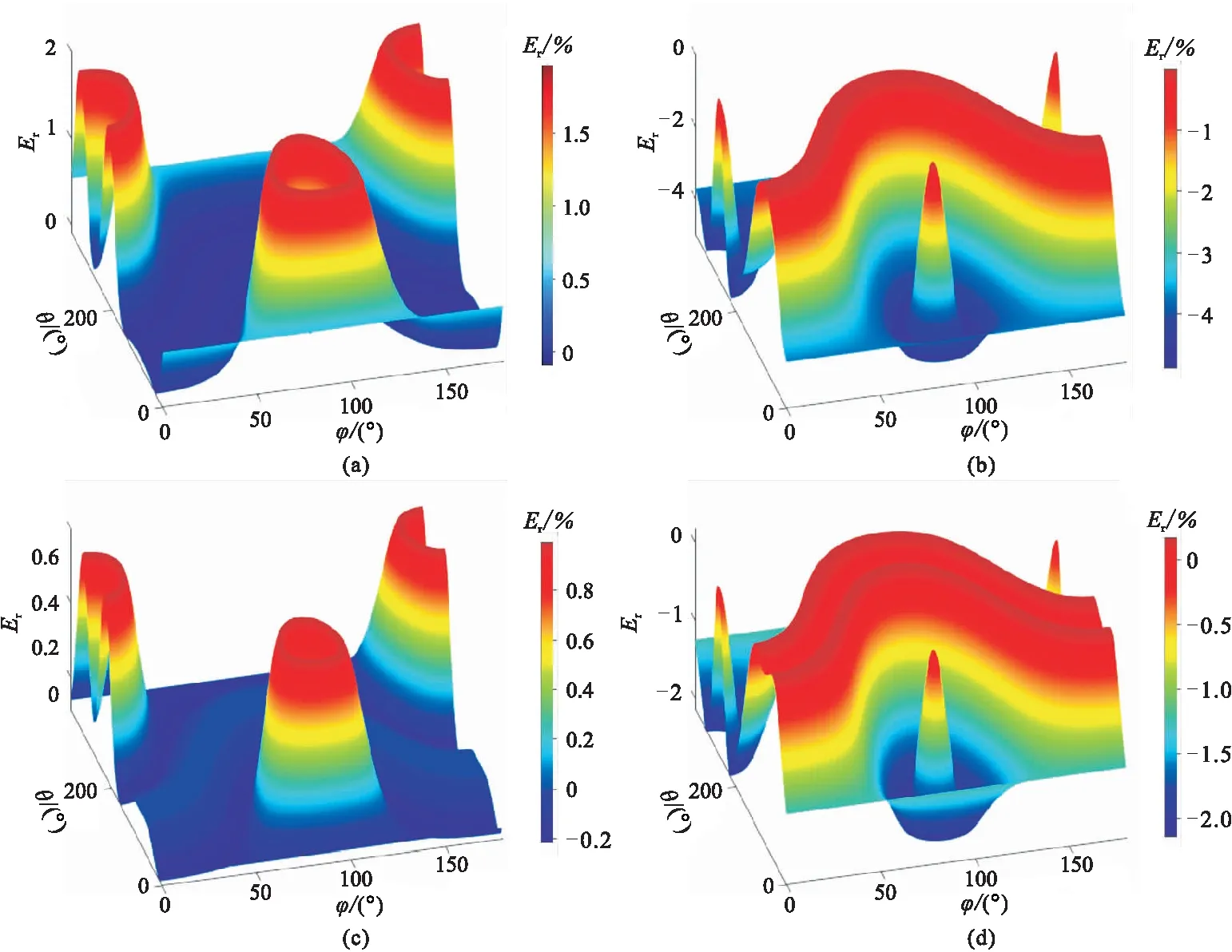
圖7 本文近似計算的TTI介質三維群速度相對誤差曲面(a)模型Ⅰ，qP波； (b)模型Ⅰ，qSV波； (c)模型Ⅱ，qP波； (d)模型Ⅱ，qSV波

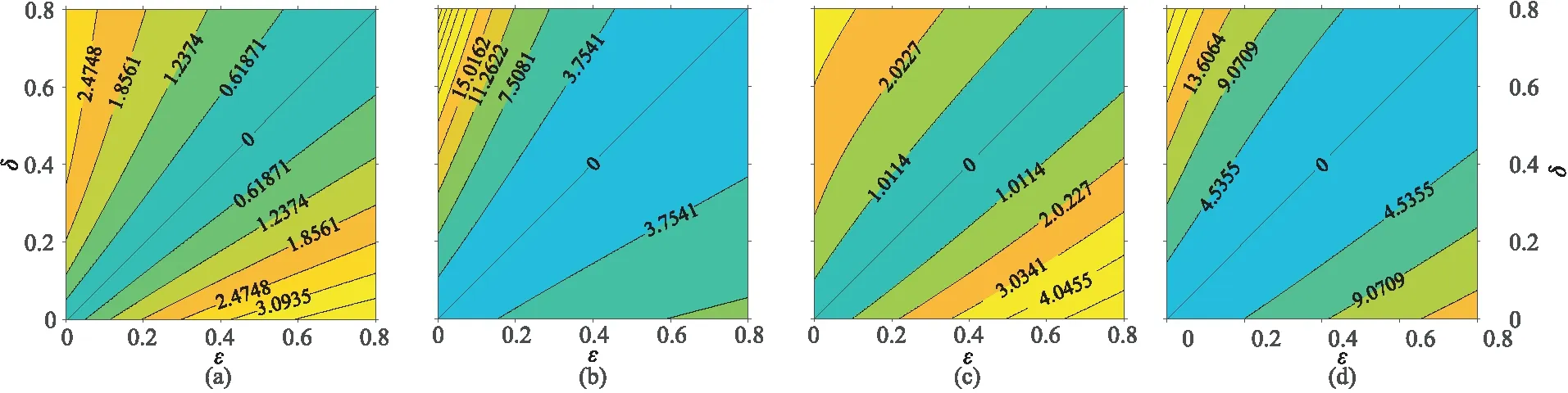
圖8 近似的三維TTI介質相、群速度最大相對誤差(%)隨ε、δ的變化等值線圖(a)qP波相速度； (b)qSV波相速度； (c)qP波群速度； (d)qSV波群速度

由圖8還可以看出，TTI介質近似qP波相、群速度在弱、中強各向異性情況下與精確解吻合較好；qP波近似相、群速度相對誤差在ε>δ時要大于ε<δ時，而qSV波近似相、群速度相對誤差則相反；ε與δ越接近，qP波和qSV波近似相、群速度的精度越高。

3 結論與認識

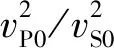
利用本文基于近似配方法推導TTI介質彈性波近似相、群速度的思想，可以進一步研究TTI介質彈性波近似頻散關系方程，通過近似頻散關系方程可推導出近似解耦的波動方程；可將qP波和qSV波相速度的近似表征代入TTI介質Christoffel方程，求解出偏振矢量的表達式，以探討TTI介質qP波和qSV波反射、透射特征。此外，在非雙曲線速度分析和疊前時間偏移的應用中，群速度近似表征可用于動校正處理和旅行時的計算等。