高精度雙斜坡輔助式混沌布里淵光纖動態應變傳感*

王亞輝 趙樂 胡鑫鑫 郭陽 張建忠喬麗君 王濤 高少華 張明江?

1) (太原理工大學, 新型傳感器與智能控制教育部與山西省重點實驗室, 太原 030024)

2) (太原理工大學物理與光電工程學院, 太原 030024)

近年來, 基于受激布里淵散射的分布式光纖傳感技術已廣泛應用于土木結構健康監測、災害預警、國防安全等諸多領域, 振動等動態參量的實時傳感和精準檢測已成為備受矚目的研究熱點.本文提出一種基于增益開關調制和雙斜坡輔助的混沌布里淵光相關域分析傳感技術, 實現高精度、大范圍動態應變監測.首先, 理論分析了單斜坡輔助系統中混沌激光固有的時延特征和功率隨機波動特性對測量精度的影響和限制; 然后,利用增益開關調制產生48.6 dB的高消光比脈沖, 使得混沌信號時延旁瓣和非零基底誘發的噪聲場被大幅抑制, 仿真結果表明聲波場信噪比提升3.31 dB, 實驗測得混沌布里淵增益譜信號背景噪聲比提升1倍, 動態應變測量精度由 ± 40.2 μe提高至 ± 23.1 μe; 最后, 利用雙斜坡輔助技術, 消除混沌激光固有功率波動的影響,動態應變測量精度進一步提升至 ± 8.1 μe, 系統穩定性良好, 且動態范圍仍保持800 μe, 為現代傳感網絡的高精度、大范圍動態應變監測提供了一種新的解決方案.

1 引 言

21世紀以來, 大型工程安全監測需求日趨嚴峻, 分布式光纖傳感技術在智能電網、油氣管網、交通基礎設施、水利工程、軍事邊境安防等重要領域已獲得廣泛應用[1,2].其中, 基于受激布里淵散射(stimulated Brillouin scattering, SBS)的光時域分析技術(Brillouin optical time-domain analysis,BOTDA)[3]和光相關域分析技術(Brillouin optical correlation-domain analysis, BOCDA)[4]由于其監測距離長、空間分辨率高、可實現溫度應變多參量監測等優勢而深受關注.然而, 傳統的SBS傳感器需通過耗時的頻率掃描過程使得探測光與泵浦光的頻率失諧量匹配光纖布里淵頻移(Brillouin frequency shift, BFS)以激發有效的SBS作用, 測得布里淵增益譜(Brillouin gain spectrum, BGS)并依其中心頻率解調光纖沿線任意位置的溫度、應變信息.因此, 傳統SBS傳感器的動態實時性受到嚴峻挑戰, 多用于靜態監測, 而不適于動態應變等參量的測量[1?4].

為滿足現代傳感網絡對動態變化參量實時監測的重大需求, 國內外研究者們針對動態應變測量范圍與監測實時性從兩個方向提出了多項創新解決方案[5,6].1)快速重構振動位置的BGS, 并依據其中心頻率實現動態應變解調.例如, 美國Voskoboinik等[7]提出將探測光頻率調制為光頻梳的免掃頻BOTDA技術可以30 kHz的速率解調BGS,以色列Peled等[8]利用任意波形發生器將探測光頻率切換速率提升至8 kHz, 哈爾濱工業大學董永康團隊[9]利用光學啁啾鏈式BOTDA系統將測量速率提升至6.25 MHz; 然而, 上述系統均屬于基于脈沖光源的BOTDA技術, 動態應變監測頻率與光纖長度成反比, 且空間分辨率受限于脈沖寬度而難以突破1 m.因此, 日本Hotate團隊[10]與上海交通大學何祖源團隊[11]分別利用壓控振蕩器構建了快速掃頻BOCDA系統, 該方案可實現振動頻率與光纖長度無關的高速單點測量, 空間分辨率達厘米量級; 但與上述BGS快速解調方案類似, 系統成本與復雜度明顯提升, 動態應變測量范圍與振動頻率無法兼顧, 實用性嚴重受限.2)無需重構BGS的斜坡輔助技術(slope assisted, SA), 該技術將探測光頻率鎖定在BGS上升沿或下降沿線性區并實時監測該頻率下動態應變引起的探測光功率變化, 根據BGS線性范圍內增益與頻移的一一對應關系實時解調動態應變[12], 斜坡輔助方案由于其成本低、技術簡便、適應性強而備受青睞.例如,Peled等[13]首次提出單斜坡輔助(single-slope assisted, SSA)BOTDA技術實現了400 Hz動態應變檢測, 但由于BGS譜寬較窄(30 MHz), 應變范圍被限制在400 μe; 為提升應變測量范圍, 布里淵增益-相移比[14]、BGS譜型調控[15]、多斜坡輔助[16?18]等技術先后被應用于BOTDA系統, 動態范圍提升至5000 μe, 然而系統復雜度持續上升且空間分辨率仍受限.因此, 何祖源團隊[19]提出雙斜坡輔助(dual-slope assisted, DSA)BOCDA技術將系統空間分辨率突破至厘米量級, 但受限于BGS譜寬其動態應變范圍僅150 μe.

最近, 本課題組提出一種大范圍動態應變監測的單斜坡輔助混沌BOCDA技術(SSA chaotic BOCDA, SSA-CBOCDA), 混沌激光獨特的寬帶光譜特性將混沌BGS本征展寬, 線性范圍擴展至55 MHz; 基于此, SSA-CBOCDA系統不僅將空間分辨率提升至3.45 cm, 而且將動態應變范圍拓展至1200 μe[20,21].然而, 混沌激光自相關旁瓣和基底在光纖沿線引入一系列SBS噪聲場, 導致系統信噪比較差, 且混沌激光固有的功率波動使得動態應變-功率響應存在大幅無規則振蕩, 這兩項因素導致SSA-CBOCDA系統動態應變測量誤差明顯高于其他SA系統.

為實現高精度動態應變監測, 本文提出一種基于增益開關調制和雙斜坡輔助的混沌布里淵光相關域分析動態應變傳感技術.首先, 本文利用增益開關將SSA-CBOCDA泵浦路進行高消光比的脈沖強度調制, 仿真結果驗證待測光纖(fiber under test, FUT)中殘留的SBS噪聲場被大幅抑制, 實驗結果顯示BGS的信號背景噪聲比(signal-to-background ratio, SBR)被明顯提升, SSA技術動態應變測量精度由 ± 40.2 μe提高至 ± 23.1 μe; 為繼續消除混沌激光固有功率波動的影響, 本文提出DSA-CBOCDA方案, 實驗驗證DSA技術可實現0.7 dB功率波動無關的動態應變解調, 最終利用該方案將動態應變測量精度提升至 ± 8.1 μe, 且測量范圍仍保持800 μe.

2 實驗裝置

斜坡輔助式混沌布里淵光相關域分析動態應變傳感技術實驗裝置如圖1所示, 混沌激光由單反饋環結構產生并經90/10的光耦合器分為兩路, 其中上支路(90%)作為探測光, 下支路(10%)作為泵浦光.探測光經邊帶調制器(sideband modulator, SBM)進行載波抑制的雙邊帶調制, 邊帶頻移量約等于光纖BFS, 且SBM由微波信號源(KEYSIGHT, N5173 B, 9 kHz—13 GHz)和電光調制器(electro-optical modulator, EOM, EOSPACE, 12.5 Gb/s)組成.調制后的混沌激光依次經可編程光延遲發生器(programmable optical delay generator, PODG, General Photonics, ODG-101)

實現傳感點的定位、摻鉺光纖放大器(erbiumdoped fiber amplifier, EDFA1, Connet, MFAS-CB-LP)將探測光功率放大至7 dBm、擾偏器(polarization scrambler, PS, General Photonics, PCD-104)降低布里淵增益的偏振敏感效應, 最終通過光隔離器(isolator, ISO)注入到FUT末端.泵浦光經強度調制器將連續混沌激光調制為脈沖混沌激光, 然后經過EDFA2(Keopsys, CEFA-C-PB-HP)和光環行器(optical circulator, OC)注入到FUT前端, 其中EDFA2將泵浦光峰值功率放大至33 dBm.兩路光在FUT中發生SBS作用, 被放大的探測光通過OC輸入到帶寬6 GHz的帶通濾波器(band pass filter, BPF, Yenista, XTM-50), 濾出的斯托克斯光被光電探測器(photodetector, PD, Finisar,XPDV2120R)接收、鎖相放大器采樣(lock-in amplifier, LIA, AMETEK, Model 7270 DSP), 最終由計算機處理與分析.FUT由30 m的普通單模光纖(G.652)構成, 其中光纖末端10 cm放置于電動位移拉伸平臺(華維浩潤, ASC-N)上以施加動態拉伸應變.需要指出, 本實驗采用的混沌激光帶寬與課題組在文獻[21]中的工作類似, 即混沌激光自相關曲線的中心峰寬度約0.36 ns, 系統空間分辨率約3.6 cm.

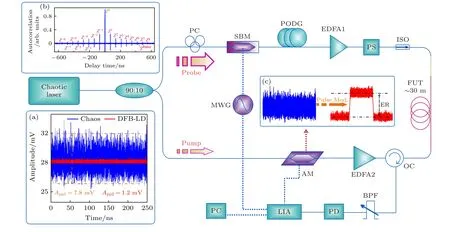
圖1 斜坡輔助式混沌布里淵光相關域分析動態應變傳感技術實驗裝置圖.插圖A為相同輸出功率下混沌激光器與分布式反饋半導體激光器的輸出信號時序, 插圖B為混沌激光自相關曲線和多階相關峰示意圖, 插圖C為連續混沌激光被調制為脈沖混沌激光Fig.1.Experimental setup of SA-CBOCDA for dynamic strain sensing.Inset A, the time series of chaotic laser and that of DFB-LD under the same output power.Inset B, the autocorrelation curve of chaotic laser and the schematic diagram of multiple order correlation peaks.Inset C, the continuous chaotic laser being amplitude-modulated into pulse chaos.

如圖1插圖A所示, 混沌激光輸出時序呈現大幅度、無規則的振蕩, 本文所使用混沌激光輸出功率為500 μW, 其時序振蕩峰峰值可達7.8 mV,是相同輸出功率下分布式反饋半導體激光器

(distributed feedback laser diode, DFB-LD)輸出時序峰峰值的6.5倍, 且兩者的均值都保持在28 mV.斜坡輔助技術中, 動態應變的大小決定了固定頻率下探測光的實時布里淵增益.根據BOCDA技術傳感原理, 探測光強度的增益過程可用如下公式表示[22]:

其中,Is和Ia分別為被SBS增益前后的探測光強度,Ip為泵浦光強度,gB為光纖布里淵增益系數,?z表示光纖中相關峰的寬度(即理論空間分辨率).由(1)式可知, 探測光強度的變化主要決定于單位空間分辨率距離內泵浦光提供的SBS增益GSBS=gBIp?z.在CBOCDA系統中, 由于混沌激光的時域振蕩特性, 泵浦光強度可表示為Ip(t)=Ip0·u(t) , 其中Ip0為均值強度,u(t) 為強度隨時間的振蕩函數(定義為泵浦光強度波動因子), 因此布里淵增益及探測光強度均隨時間大幅度振蕩; 同理可知, 傳統基于DFB-LD的傳感系統中, 泵浦光強度可近似表示為Ip=Ip0, 故由泵浦光強度波動引起的增益波動極其微弱.

此外, 探測光增益還會受到光纖中相關峰的影響.在理想的CBOCDA系統中, 由于混沌激光時序自相關曲線的類δ函數特性, 任意距離FUT中存在唯一的0階相關峰z0, 僅在該峰內激發有效的SBS效應.然而, 混沌激光固有的時延特征(time delay signature, TDS)導致其自相關曲線中心峰兩側存在一系列旁瓣峰, 且自相關基底也呈現隨機起伏的振蕩狀態; 上述旁瓣峰zn,n=±1,2,···和非零基底zbase會在FUT中激發一系列的SBS聲波場.如圖1插圖B所示, 假設以此混沌激光為探測信號, 當FUT長度為120 m時, 除中心位置外,FUT中還存在至少8階旁瓣峰, 即同時激發產生了至少16個強度明顯的噪聲SBS聲波場; 此外,非零基底zbase也會激發隨光纖長度不斷累積的微弱噪聲場.因此, 中心峰位置處的GSBS被進一步干擾惡化, 最終測得的探測光強度可表示為

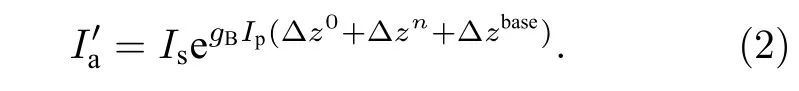
為了抑制系統背景噪聲, 本課題組已經提出時域門控方案[23], 如圖1插圖C所示, 連續混沌激光被調制為脈沖混沌激光, 脈沖持續時間τp與單反饋混沌環腔長對應時間一致.此時, 混沌泵浦光強度修正為

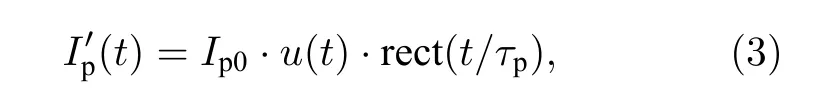
其中 r ect(ξ) 為矩形脈沖函數, 僅當時取值為1.因此, 脈沖混沌泵浦光理論上可使光纖中僅存在z0,zn,n=±1,2,···和zbase則被完全抑制; 實際上, 脈沖調制消光比將直接影響噪聲場的抑制程度, 由于混沌激光的振蕩特性, 本文定義消光比(extinction ratio, ER)為脈沖高電平時間內信號強度均值與脈沖基底時間內信號強度均值之比;當ER值較大時以τp時間內z0激發的SBS效應為主, 當ER值較小時隨光纖長度逐步累積(T?τp時間內)的zn,n=±1,2,···和zbase噪聲增益占據主導.

綜上所述, SA-CBOCDA系統中泵浦光為探測光提供的SBS增益可表示為

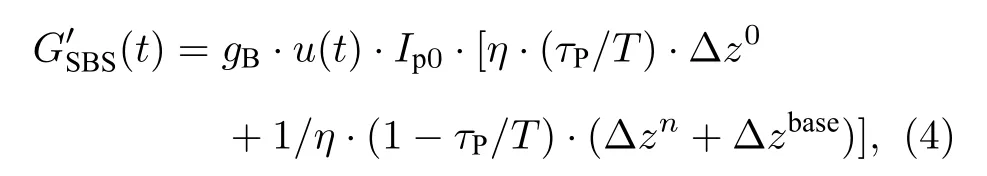
其中,τp和T分別表示最佳的脈沖持續時間和脈沖信號周期;η表示泵浦脈沖調制ER值, 且η1 ,η=1表示未施加脈沖調制.由(4)式可知, SACBOCDA系統中,同時受泵浦光強度波動因子u(t) 和脈沖調制消光比η的影響, 探測光強度存在較大的固有波動和噪聲干擾; 由于探測光功率(確定的光纖系統中, 探測光強度變化可等價于探測光功率變化)與動態應變的線性對應關系, 導致動態應變測量精度明顯弱于基于DFB激光的SA系統.為抑制系統噪聲增益源, 本文提出基于增益開關的高消光比脈沖調制和基于雙斜坡輔助的免泵浦功率波動依賴技術, 最終實現高精度的動態應變測量.

3 實驗結果與分析

3.1 基于增益開關調制的動態應變精度提升

原始時域門控CBOCDA系統中, 連續混沌泵浦光被EOM調制為脈沖光, 通過調節射頻脈沖電壓控制信號消光比; 然而, EOM自身特性只能提供小于40 dB的消光比, 且存在插入損耗大、消光比不穩定、偏壓控制復雜等缺點[24], 導致傳統時域門控系統的脈沖消光比差、系統復雜度高、背景噪聲抑制不完全.因此, 提出基于增益開關(gain switch, GS)的調制方案, 實現高且穩定的消光比而進一步提升信噪比(signal-to-noise ratio, SNR)、降低系統復雜度.

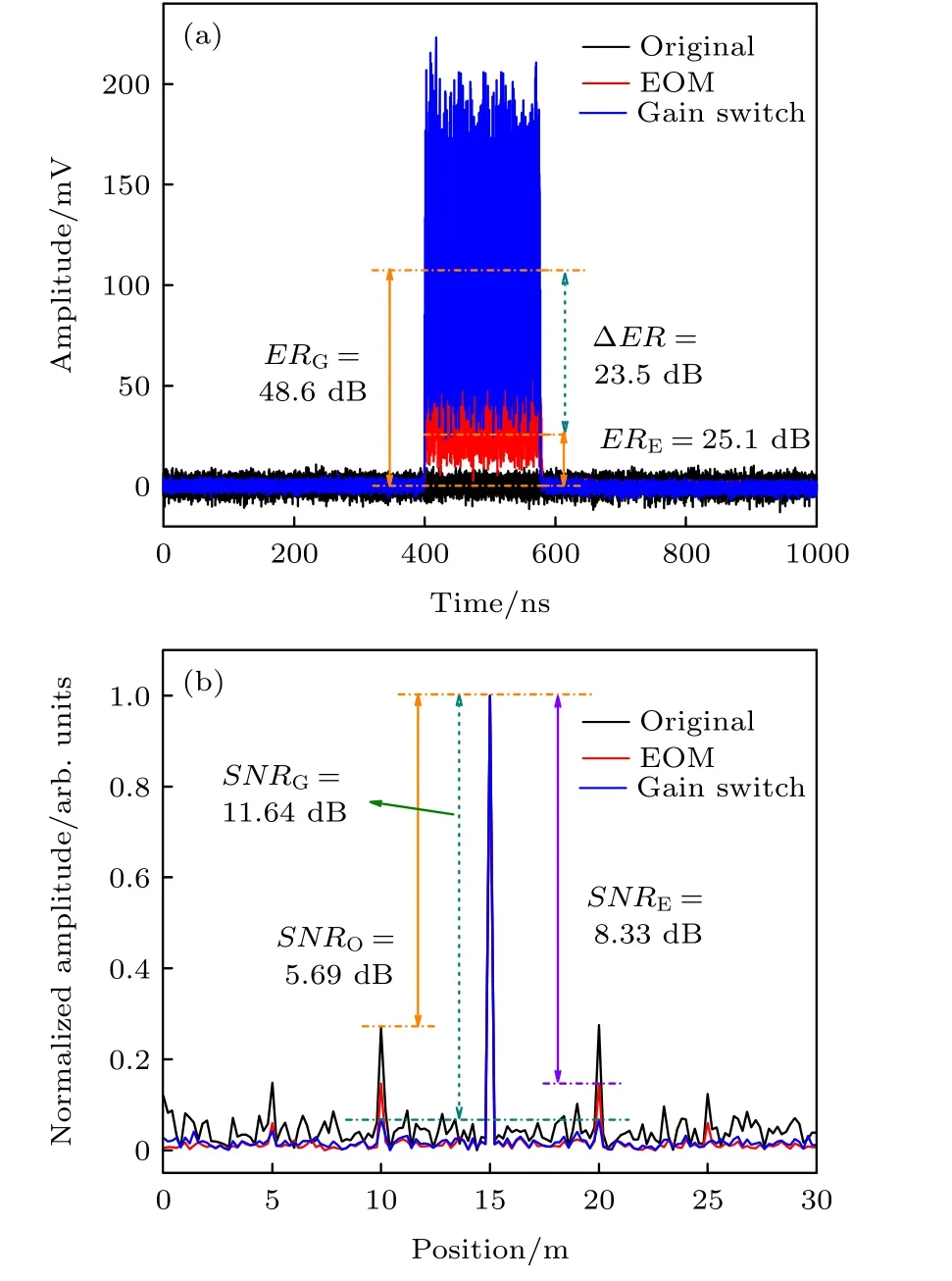
圖2 不同調制方式及作用效果 (a)不同調制方式下脈沖混沌光時序及消光比; (b)不同調制方式下仿真的混沌受激布里淵聲波場強度及信噪比Fig.2.Different modulation methods and the corresponding effects: (a) The time series of pulse chaos and ERs of these under different modulation modes; (b) simulation results of chaotic SBS acoustic field amplitude and the corresponding SNR.

圖2 (a)所示為實驗測得原始狀態、EOM調制與GS調制混沌激光時序, 并對不同調制方式下的消光比ER=20·log(Vpeak/Vbase) 進行了對比分析.由圖2(a)可以看出, EOM調制提供僅25.1 dB的ER值, GS調制消光比可達48.6 dB, 比EOM調制提升了約23.5 dB.根據(4)式可知, GS的高消光比調制可大幅抑制zn,n=±1,2,···和zbase噪聲峰, 為了驗證這一效果, 本文首先仿真模擬了不同調制情況下的SBS聲波場強度.如圖2(b)所示, 黑色曲線為連續混沌激光入射30 m光纖中時的聲波場分布情況, 已知混沌激光時延腔長為5 m, 因此除光纖中心15 m處z0外, 10與20 m處存在強度較大的z±1, 5與25 m處甚至存在z±2; 此外, 混沌激光自相關基底激發的SBS噪聲強度也被清晰觀測到.混沌SBS聲波場信噪比定義為中心峰強度Acp與噪聲峰峰值強度Anp的比值SNR=10·log(Acp/Anp), 則基于連續混沌激光的SBS聲波場SNR約為5.69 dB.EOM調制系統中,z±1和zbase被抑制效果明顯,z±2幾乎完全消失, SNR值也提高至8.33 dB, 然而未完全消除的噪聲峰仍會隨光纖長度持續累積并惡化探測光的SBS增益.GS的高消光比調制使得z±1,2和zbase幾乎均被完全抑制, SNR提升至11.64 dB, 約為基于連續混沌激光系統的2倍, 且與EOM調制系統相比也有3.31 dB的提升.

根據本課題組的早期研究結果[23,25,26], CBOCDA系統噪聲峰的抑制效果將直接體現為混沌BGS的SBR值水平, 因此, 本實驗繼續對比了不同調制方式下的混沌BGS.為了更好地比較分析BGS包絡及SBR, 將EOM調制和GS調制系統中測得的混沌BGS進行了歸一化處理, 如圖3所示.可以看出, GS調制系統背景噪聲水平明顯更低, 其SBR值為15.22 dB, 約為EOM調制系統的2倍.此外, 圖3插圖為測得的原始增益譜, 可以看出, GS高消光比調制顯著提升了SBS增益強度, 通過PD探測到約0.013 mV的峰值增益增量.GS調制實現了與長腔反饋混沌激光[21]相同的噪聲抑制效果, 且實用性更強、易于實現長距離高信噪比BGS測量.此外, 已知SA技術是通過探測鎖定頻率下的布里淵增益實現動態應變解調的, 因此, 優化后的增益譜可促進理論上獲得更精確的動態應變測量.

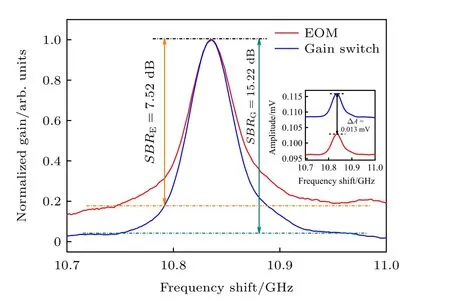
圖3 不同調制方式下的歸一化混沌布里淵增益譜及其信號背景噪聲比; 插圖為測得的原始布里淵增益譜Fig.3.Normalized chaotic BGSs and SBR analysis of these,under different modulation modes.Inset view: the measured original BGSs, corresponding to the main view.

基于圖1所示的實驗裝置, 泵浦路分別利用EOM和GS實現脈沖強度調制, 探測光頻率鎖定在混沌BGS下降沿10.865 GHz處, 通過電動拉伸位移平臺的往復運動提供動態應變.為保證探測光功率對動態應變的線性響應, 本實驗施加的動態應變大小為0—800 μe, 消除由功率-應變轉換系數引起的測量誤差[20].圖4(a)和圖4(b)分別給出了EOM調制與GS調制下SSA-CBOCDA系統測得的動態應變時序及其正弦擬合曲線, 由圖可知, 兩種調制方式下動態應變值均可被準確地解調.為了表示測量精度, 本文首先比較了兩條正弦擬合曲線的相關系數R2, GS調制系統的相關系數0.9793略大于EOM調制系統, 但均接近于1, 表明兩者的擬合結果均較好, 但是GS調制系統的相關性更高.此外, 本文詳細分析了兩種調制方式下的動態應變測量誤差, 如圖4(c)所示, 藍色和紅色點圖分別表示EOM調制、GS調制系統中15次獨立重復測量的動態應變誤差均值及不確定度, 插圖為單次測量誤差的測算依據和典型結果.EOM調制系統中誤差明顯更大, 標準偏差σE為 ± 40.2 μe, 相對誤差達 ± 5.0%.經過GS調制改進, SSA-CBOCDA系統動態應變測量誤差σG降低至 ± 23.1 μe, 相對誤差縮小為 ± 2.9%.此外, 不同調制系統中標準偏差的不確定度均較小, 進一步表明精度測量結果準確性高、系統穩定性好.圖4(d)所示為兩種調制方式下測得的動態應變的振動頻率, 結果表明基頻1.3 Hz和二次諧振頻率2.6 Hz均可被準確檢測; 需要指出, 本實驗采用的電動位移拉伸平臺由一對步進電機控制, 電機的低速往復運動導致振動頻率較低, 下一步將考慮使用壓電陶瓷振蕩器提供高頻的動態應變.

綜上所述, 在基于增益開關調制的SSA-CBOCDA系統中, 混沌激光旁瓣峰和非零基底引起的SBS增益噪聲被大幅抑制, 動態應變測量精度提升了約1.7倍.然而, 由(4)式可知, GS調制并不能消除由混沌激光固有功率波動u(t) 導致的測量誤差; 此外, GS調制會導致脈沖高電平持續時間內更強的功率波動, 因此本文提出雙斜坡輔助技術繼續提升動態應變測量精度.

圖4 不同調制方式下的動態應變測量結果 (a) EOM調制系統動態應變測量時序及正弦擬合曲線; (b) GS調制系統動態應變測量時序及正弦擬合曲線; (c)兩種調制方式下的動態應變測量誤差, 插圖為單次測量典型結果; (d)兩種調制方式下的動態應變頻率Fig.4.The results of dynamic strain measurement under different modulation modes: (a) Time series and sine fitting curve of dynamic strain in EOM modulation system; (b) time series and sine fitting curve of dynamic strain in GS modulation system;(c) measurement error of dynamic strain under two modulation modes, inset view is the typical result of a single measurement;(d) vibration frequency under two modulation modes.

3.2 基于雙斜坡輔助的動態應變精度提升

斜坡輔助技術中, 上升沿鎖定頻率v+下的對數型探測光增益可表示為[19]

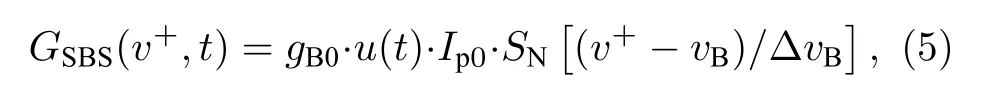
其中,gB0表示有效布里淵增益系數且僅與光纖材料、光路偏振狀態有關(在確定的系統中可認為是常 數),vB表示應 變、溫 度 等引起的BFS, ?vB為BGS線寬(本實驗中混沌BGS線寬約50 MHz),SN(vB)為歸一化的BGS.

同理可得, 下降沿鎖定頻率v?下的對數型探測光增益可表示為

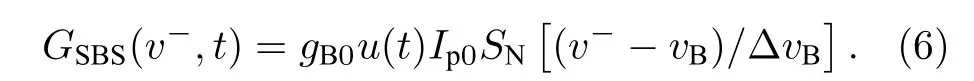
由(5)式和(6)式可以發現, 無論頻率鎖定在上升沿或下降沿, 探測光增益均與泵浦光強度(即泵浦光功率)成正比, 因此可得兩個確定頻率下的增益比RB為

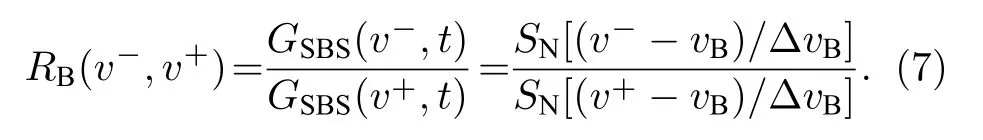
經過雙斜坡比值分析可知, 動態應變大小僅與鎖定頻率下的增益大小有關, 與泵浦光功率無關.

圖5詳細分析了DSA方法的原理, 以歸一化的混沌BGS(藍色虛線)為例, 分別取上升沿與下降沿中心頻率v+,v?為鎖定頻率, 此時兩點頻率間隔恰好為BGS線寬v??v+=?vB, 保證最大化利用混沌BGS的本征寬譜特性; ?v表示動態應變引起的相對BFS, 易知 ?v=0 時RB=0 , 保持間隔 ?vB并以v+,v?為中心在BGS譜線上取不同大小應變引起的 ?v對應的增益值, 最終求得如圖5紅色實線所示的RB分布曲線.由圖可知,RB曲線至少擁有40 MHz的線性區間(紫色圓點所示, –20—+20 MHz), 即可精確測量的動態應變范圍至少為800 μe.

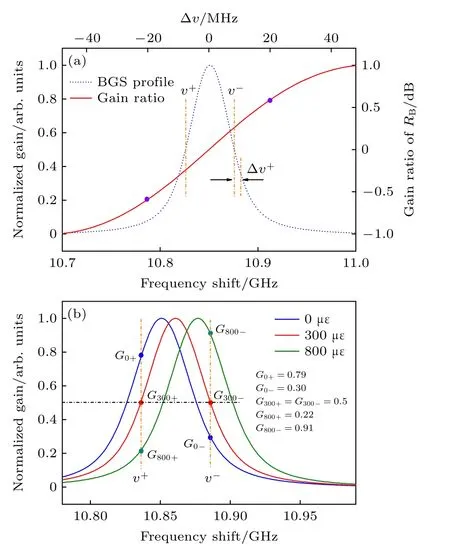
圖5 雙斜坡輔助技術原理示意圖 (a)布里淵增益比的理論分析; (b)布里淵增益比實驗標定的理論模型Fig.5.Principle of DSA method: (a) theoretical analysis of RB ; (b) theoretical model for experimentally calibrating R B.

如前所述, 為了免除光纖松弛對測量結果的影響, 本實驗將光纖拉伸段施加約300 μe的預拉伸, 并基于此狀態下的增益譜選定頻率v+,v?.如圖5(b)所示, 此時G300?≈G300+≈0.5 , 即RB≈0 dB; 當施加應變分別為0和800 μe時, 根據圖中圓點標識, 計算得增益比值分別約為–0.42和0.62 dB, 均保持在圖5(a)RB曲線所示的線性區內.具體實驗時, 如圖6(a)所示, 分別測量兩個頻率下施加不同大小準靜態應變時的探測光時序, 計算得不同應變對應的RB曲線; 由圖6(a)可以看出,0與800 μe時RB取值與理論分析基本一致, 當應變以200 μe步進從0 μe增加至800 μe時,RB幾乎呈現線性上升趨勢, 且300 μe時RB值近似于0 dB.不同應變對應RB的均值被進一步提取并做線性擬合, 如圖6(b)所示, 相關系數RR2約等于0.9990表明了RB與應變值的良好線性關系; 根據曲線斜率可得, 該DSA系統的最終增益比—應變轉換系數Cs約為0.0012 dB/μe.

為了驗證DSA技術可以消除泵浦功率波動影響, 本文測量了基于上升沿和下降沿中心頻率鎖定的SSA動態應變響應時序, 動態應變大小為0—600 μe, 同時手動添加了泵浦光先減后增的大范圍功率波動.如圖7(a)所示, 無論上升沿或下降沿頻率鎖定, SSA技術均可實時反映動態應變引起的布里淵增益強度變化, 然而其響應時序呈現與泵浦光功率一致的先下降后上升趨勢, 峰值功率波動達0.7 dB, 無法利用功率-應變轉換系數準確解調動態應變大小.根據DSA技術原理, 將圖7(a)中的兩列時序進行比值計算并利用Cs解調便得圖7(b)中藍色曲線所示動態應變序列.可以看出,動態應變大小已被準確還原, 利用正弦擬合曲線進一步驗證了較好的動態應變測量正確度(相關系數R2≈0.9642).

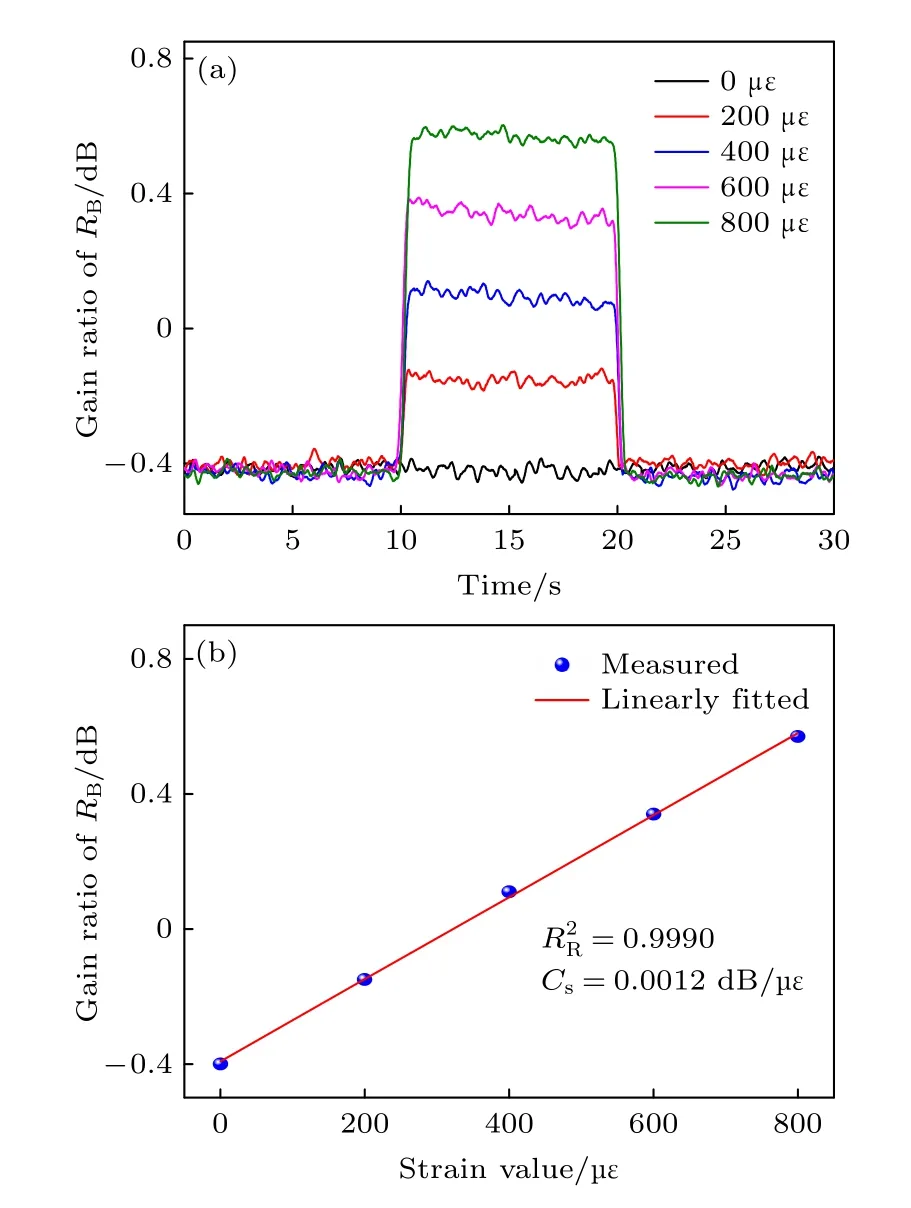
圖6 雙斜坡輔助系統的增益比-應變轉換系數 (a)不同大小準靜態應變對應的增益比曲線; (b)根據線性擬合曲線計算的轉換系數Fig.6.Estimate of the conversion coefficient, C s , between the strain value and R B in DSA system: (a) TheRB curves under different quasi-static strain; (b) final coefficient calculated from the linear fitted curve.

基于上述驗證實驗和轉換系數, 本文在僅有混沌激光自身功率波動的情況下, 利用DSA技術進行了動態應變大小及精度的最終測定.如圖8所示, 圖8(a)中藍色曲線為實際測量的動態應變時序, 0—800 μe動態應變被準確測量; 對測量值做如紅色點圖所示的正弦擬合, 擬合相關性高達0.9972; 同時如圖8(b)中藍色點圖所示, 通過15次獨立重復測量計算得應變測量誤差σD為 ± 8.1 μe,插圖即為單次測量誤差的測算依據和典型結果; 相對誤差下降至 ± 1%, 動態應變測量精度明顯提升.動態應變標準偏差的不確定度僅± 1.0 μe, 表明了雙斜坡輔助系統具有更好的測量準確度和系統穩定性.此外, 動態應變振動基頻1.3 Hz也被準確檢測, 動態應變頻率與SSA系統測量結果一致(電動位移平臺的運動速度并未改變).

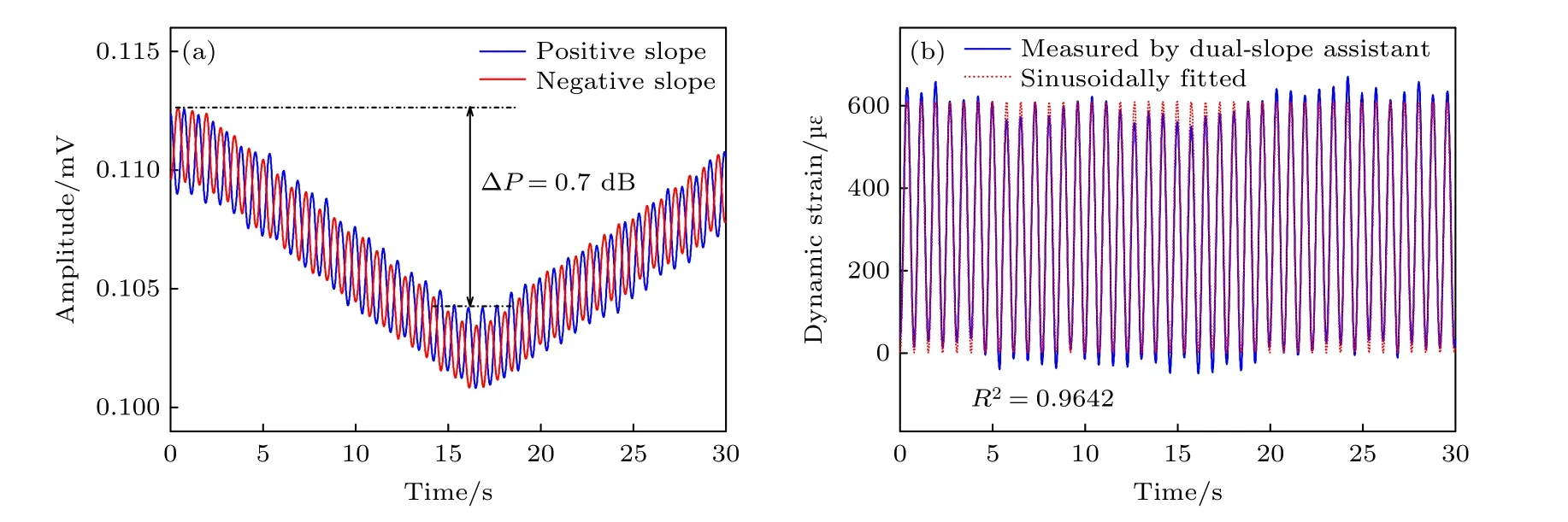
圖7 雙斜坡輔助技術消除泵浦功率波動影響的驗證實驗 (a)手動施加泵浦光功率波動時利用單斜坡輔助技術測得的動態應變響應時序; (b)雙斜坡輔助技術解調的動態應變大小Fig.7.The verification experiment of pump-power-independent measurement by using DSA method: (a) Measured Brillouin amplitude using SSA method when a dynamic strain is applied with a manual change of pump power; (b) measured dynamic strain using DSA method.

圖8 施加0?800 μe時的雙斜坡輔助系統動態應變測量結果 (a)動態應變測量時序及正弦擬合曲線; (b)動態應變測量誤差,插圖為單次測量典型結果; (c)動態應變振動頻率Fig.8.Measurement results of DSA system when a dynamic strain of 0?800 μe is applied: (a) Measured time trace and sine-fitted curve; (b) measurement error, inset view is the typical result of a single measurement; (c) vibration frequency.

4 結 論

本文提出了一種高精度的斜坡輔助式混沌布里淵光相關域分析動態應變傳感技術.首先, 理論分析了混沌激光固有的功率隨機波動特性、自相關曲線旁瓣峰和隨機基底對SA-CBOCDA系統測量精度的影響和限制; 其次, 利用增益開關實現48.6 dB的高消光比脈沖調制, 與EOM調制系統相比, 仿真得GS調制可將SBS聲波場的信噪比提升3.31 dB、實驗測得GS調制可將混沌BGS的信號背景噪聲比提升1倍, 實驗證明動態應變測量精度由 ± 40.2 μe提高至 ± 23.1 μe, 相對誤差從± 5.0%縮小為 ± 2.9%, 且標準偏差不確定度由± 3.3 μe降低至 ± 2.5 μe; 最后, 實驗驗證了雙斜坡輔助技術可免除大范圍泵浦功率波動的影響,DSA-CBOCDA系統將動態應變測量精度再次提升至 ± 8.1 μe, 相對誤差僅 ± 1%, 動態范圍仍保持0—800 μe, 且標準偏差不確定度僅 ± 1.0 μe,實現了高精度、大范圍、高穩定的動態應變傳感.與SSA-CBOCDA系統相比[20,21], 本文方案的動態應變測量精度提升顯著, 約為原來的5倍, 測量范圍略微下降為原來的 2 /3 , 下一步將繼續開發多斜坡輔助技術拓展動態范圍.與現有的DSA系統相比[16,19], DSA-CBOCDA系統測量精度基本一致,但是測量范圍遠大于150 μe.此外, 本文動態應變振動頻率受步進電機低速運動和LIA低采樣率的限制而保持在Hz量級, 未來研究中將采用壓電陶瓷振蕩器提供高頻的動態應變和高速數字示波器進行實時采樣, 將振動頻率提升至kHz量級.綜上所述, 本文實現了一種高精度、大范圍動態應變監測的DSA-CBOCDA系統, 同時保持厘米級高空間分辨率, 將為現代工業中動態變化參量的精準定位和實時監測提供一種新型解決方案.