一種不確定性捆扎線束電磁耦合效應的廣義等效建模方法*

肖培 李佳維 賀佳港 李錦新 劉柱 李高升?

1) (湖南大學電氣與信息工程學院, 長沙 410082)

2) (湖南大學信息科學與工程學院, 長沙 410082)

線束在實際布線過程中存在空間布局特性, 其芯線數目大、空間任意彎曲以及位置不確定等特點給線束耦合干擾的建模與分析帶來了挑戰.不確定性全線束模型耦合干擾的數值仿真對計算能力提出了更高要求,甚至無法進行有效計算.因此, 本文提出了不確定性捆扎弧形線束電磁耦合效應的廣義簡化建模方法, 考慮了捆扎線束內導線相對位置的不確定性.基于高斯分布和樣條插值方法, 建立了不確定性捆扎線束內導線的位置, 根據多導體傳輸線理論確立了等效線束的幾何截面結構參數, 通過圓弧和正弦捆扎線束數值算例驗證了本文方法的有效性.

1 引 言

機電系統電磁耦合通道的等效建模是復雜電子系統電磁兼容分析的重點與難點[1,2].線纜是機電系統電磁耦合干擾的主要傳導路徑, 現有文獻表明, 線纜產生的電磁干擾是大部分系統不符合電磁兼容規范的主要原因.線纜電磁耦合問題的研究是電子系統電磁兼容研究內容的關注重點, 對系統電磁兼容性能分析具有重要作用[3?6].圖1所示為某設備控制信號線束, 存在空間布局特性, 其芯線數目大、空間任意彎曲以及位置不確定(導線相對位置隨線長發生變化)等特點給線束電磁耦合干擾的建模與分析帶來了挑戰.不確定性全線束模型耦合干擾的數值仿真對計算能力提出了更高要求, 甚至無法進行有效計算.因此, 需要提出更有效的建模方法, 來解決機電系統干擾傳輸路徑建模問題.

圖1 控制器信號線纜束Fig.1.Controller signal cable bundle..

線束等效建模方法(equivalent cable bundle method, ECBM)目的在于將多根導線等效為不超過4根導線的簡化模型.2008年, 國外學者首次提出了多導體傳輸線ECBM方法[7], 對理想導電平面上的多導體線束電磁耦合效應進行了等效建模,并應用于汽車復雜線束耦合電流的預測, 其主要思路為: 根據線束終端阻抗值與其特征阻抗值的比較, 將線束最多分為4組; 利用多導體傳輸線理論得到簡化線束的結合截面結構參數; 確立簡化線束終端等效負載.此外, ECBM方法被拓展應用于理想導電平面上多導體傳輸線電磁輻射發射的建模[8,9]以及差分線束上電磁耦合電流的計算[10].

國內一些學者對ECBM方法進行了拓展應用, 提出了線束串擾建模的ECBM方法, 并對理想導電參考地面上、理想金屬圓柱腔內及正交參考面等場合進行了有效性驗證[11?13].此外, 一些學者成功地將ECBM方法應用于汽車線束的電磁干擾建模[14].另有一些學者提出了時域有限差分計算方法, 拓展研究了ECBM方法在汽車線束串擾和輻射敏感度的預測問題[15,16].

現有的ECBM方法主要解決了確定性布局線束的建模問題, 而在工程應用中, 線束布局往往具有不確定性.因此, 本文在已有ECBM方法基礎上, 提出了不確定性捆扎線束電磁耦合效應的廣義ECBM方法.考慮了線束內導線位置的不確定性, 使用高斯分布和樣條插值獲取不確定性捆扎線束內導線的位置, 利用導線子段之間存在換位關系求得線束的分布電感和電容矩陣參數, 根據多導體傳輸線理論得到簡化線束的幾何截面結構參數, 最后通過圓弧形和正弦弧形線束數值算例驗證本文方法的有效性.

2 不確定性捆扎線束電磁耦合問題

2.1 捆扎線束不確定性分布特點

圖2(a)為理想導電平面上弧形捆扎線束, 圖2(b)為其電路連接示意圖.可以看出, 捆扎線束內導體并非絕對平行, 其相對位置沒有固定, 線束內導線相對位置在線長方向上具有不確定性變化特點.而線束內導線位置直接影響傳輸分布參數值, 因此,導線間的電感和電容矩陣隨著線長變化.

2.2 線束電磁耦合建模問題

圖3為圖2中不確定性捆扎弧形線束的幾何截面結構, 線束內包含多根導線, 虛線表示線長方向上任意位置處線束所限區域.假設線束橫截面的幾何形狀在線長方向基本保持為圓形.本文針對不確定性捆扎線束電磁耦合干擾建模問題, 利用多導體傳輸線理論將不確定性捆扎的多根導線模型簡化為單根線模型, 即用單根線的電磁耦合效應等效描述多根線的電磁耦合效應.

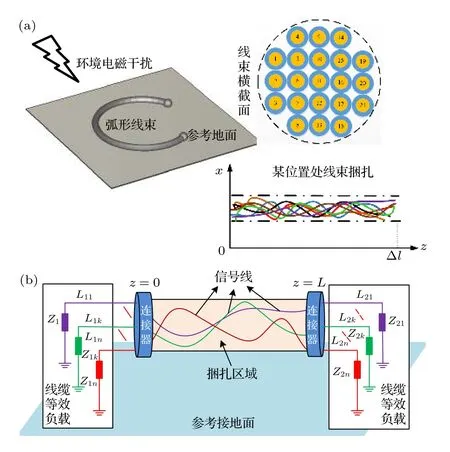
圖2 設備互連線束示意圖 (a)弧形捆扎線束; (b)線束電路連接示意圖Fig.2.Schematic diagram of equipment interconnection wiring cable harness: (a) Arc-shaped binding cable harness;(b) circuit connection diagram.

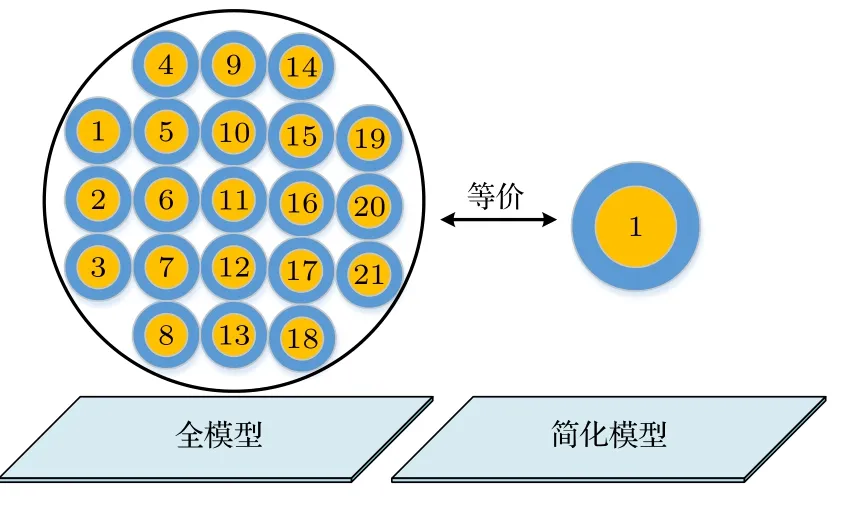
圖3 不確定性捆扎線束簡化建模Fig.3.Simplification modeling of uncertainty binding cable harness.

3 不確定性捆扎線束電磁耦合簡化建模方法

3.1 簡化線束單位長度參數的計算

圖4為位于理想導電平面上的n根導線, 假設ri和rj為其中任意兩導體半徑,hi和hj為導體的對地高度,Sij為導體間距, ?ri和 ?rj分別為導線絕緣層厚度.則導線單位長度電感計算公式為[17]

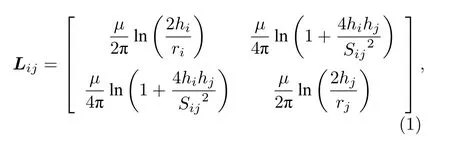
式中,μ為磁導率, 約為 4 π×10?7H/m,Lij中對角元素表示導線單位長度自電感, 非對角元素表示導線單位長度互電感.由(1)式可知, 導線相對位置會影響導線電感和電容參數.

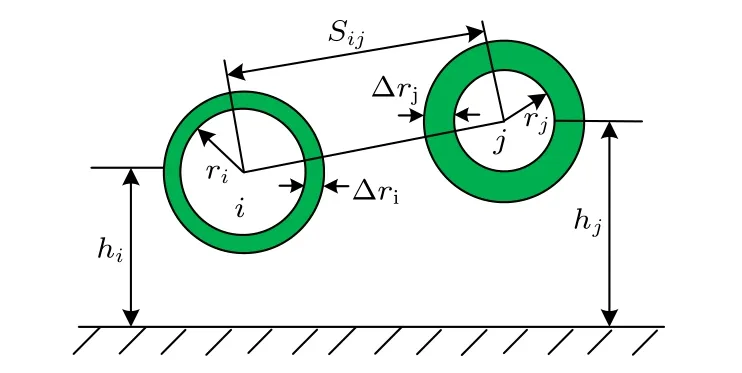
圖4 雙導體傳輸線幾何截面結構Fig.4.Cross-sectional geometry of double conductors.

當導體外層涂覆絕緣層材料時, 絕緣層材料的介電極化效應在電磁場作用下產生束縛電荷, 導體表面同時還分布有自由電荷.絕緣層非均勻介質效應使得理想電容的計算公式不再適用, 即1.基于鏡像法原理, 單位長度導體電容參數計算公式如下[18]:

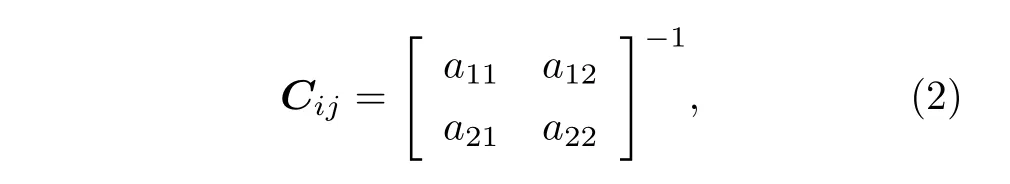
式中,a11,a12,a21和a22分別為

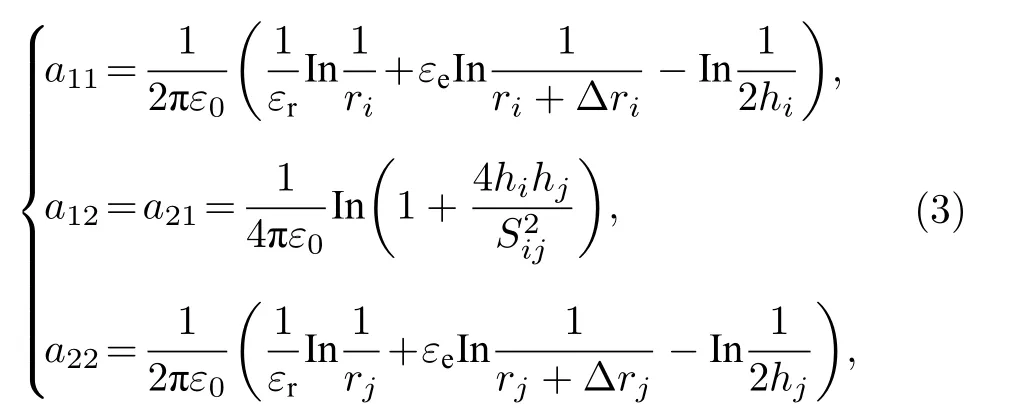
其中,ε0為空氣的介電常數, 約為 8.85×10?12F/m.εr為相對介電常數,εe=(εr?1)/εr.

對于包含n根理想無損耗導體的線束模型, 其傳輸線方程為

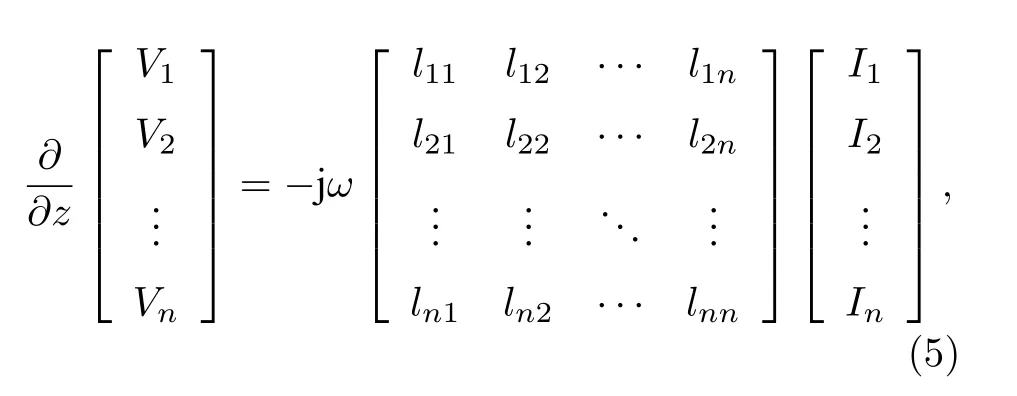
式中,V1,V2,···,Vn和I1,I2,···,In分別為單位長度導線上的電壓和電流.為了計算簡化線束單位長度電容Ceq和電感Leq, 需滿足以下近似:

1)定義簡化線束等效電流Igc為原線束中n條導線的電流和

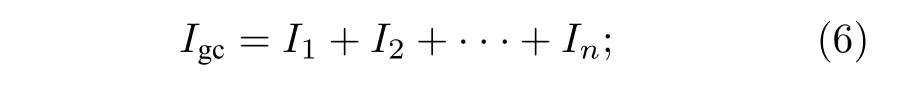
2)定義簡化線束等效電壓Vgc與原所有導線具有相同的電壓

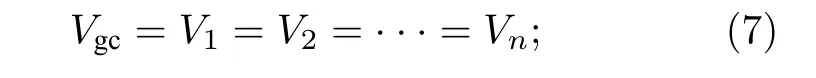
3)假設線束模型中所有導體上的電流分布相同, 則任意一根導線的共模電流Ix為

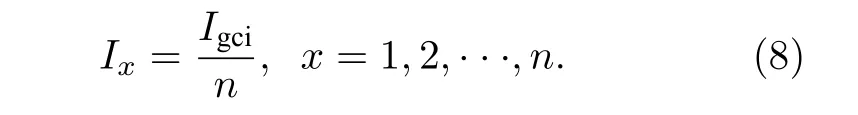
將(7)式代入傳輸線方程 dI/dz=?jωCV并聯立(6)式和(8)式得:

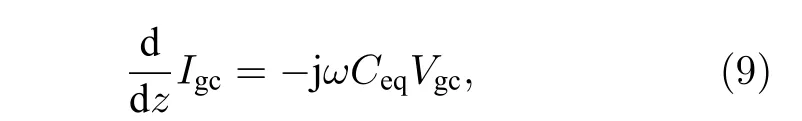
此外, 將(6)式代入方程 dV/dz=?jωLI并聯立(7)式和(8)式得:

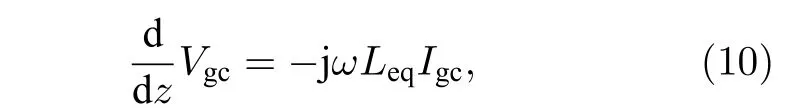
需要注意的是本文提出的線束廣義等效建模方法, 利用解析方法求解多導體單位長度分布參數時, 導線間距需滿足寬間隔條件, 即相鄰導線間的距離與導線半徑之比不小于4.否則導體間的鄰近效應會導致導體周向表面的電荷與電流分布不再均勻, 此時需要采用數值方法來獲取分布參數.

3.2 簡化線束幾何截面結構參數的確立

(1)不確定性捆扎建模

雖然線束內任意位置處導線相對位置具有不確定性, 但受限于線束兩端連接器插件, 它們的始端和終端是確定的.文獻[19]研究表明線束內導體相對位置在長度方向上滿足高斯分布特點, 針對導線模型中不連續問題, 采用隨機樣條插值法取得了良好效果.首先, 利用MATLAB軟件生成具有高斯分布特點的隨機位置, 如圖5(a)所示.然后, 通過樣條插值法在其他位置插入更多的數值點, 如圖5(b)所示, 從而將線束劃分為一系列的均勻子段.需要注意的是, 這些子線段長度需滿足以下其一: 1)每段長度 ?l應小于最小波長的1/10, 以確保最高頻率波的空間分辨率; 2)為保證線束連續性, 樣條線段應有足夠多子段(不少于10個).利用上述兩個標準所確定的較小子段, 使用三次樣條插值技術的分段多項式確立級聯線段, 如圖5(c)所示.

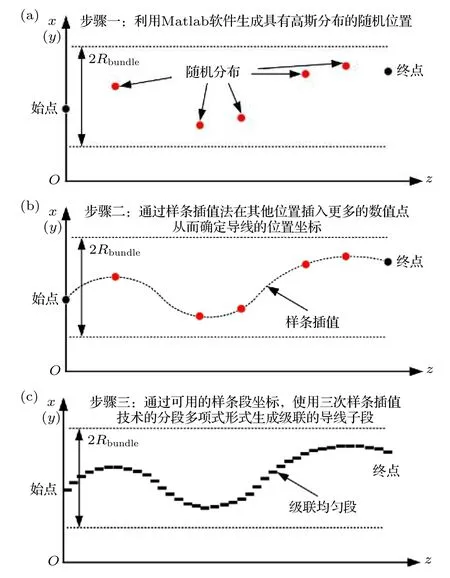
圖5 不確定性線束建模步驟 (a)線束始端的確立;(b)基于樣條插值法的線束位置; (c)分段級聯Fig.5.Modeling steps for uncertainty cable harness: (a) Determination of the beginning end; (b) location of the cable harness based on spline interpolation; (c) sectional cascade.

由于線束內導線相對位置沿線長方向發生變化, 線束電感和電容參數是非恒值, 這些值采用有限元等數值方法可求得.然而, 由于線束內有多根導體, 需要多次求解計算模型, 耗費時間長.因此需要提出更有效的方法計算不確定性捆扎線束的傳輸參數.

總的來說，灌溉農業的主要效益是解決糧食安全問題和增加農民收入的社會效益。因而，灌排事業的發展必須要得到國家的大力支持，包括國家的政治意愿，以及在制定政策、發揮領導作用、制定發展規劃、提供資金和技術支撐、改革管理機構和管理體制等方面的支持。中國在灌排領域的發展成就、政策及目標和模式舉世矚目，獲得了國際社會的高度評價和認可。

本文研究模型中線束內所有導線線型相同, 子段具有相互獨立性, 即所在橫截面中任意導線的位置與該導線在其他段中橫截面的位置互不影響.由于橫截面的形狀是固定的, 導線只在每個分段連接點處于一個突變的位置, 以9根捆扎線束為例, 如圖6所示.

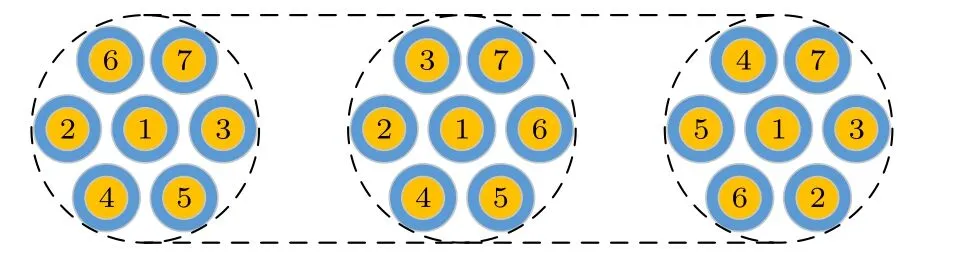
圖6 線束內導線之間的換位示意圖Fig.6.A schematic diagram of transposition between conductors in the cable harness.

取其中相鄰的幾段線束, 子段1變為子段2時, 3號導線和6號導線的位置相互變換; 子段2變成子段3時, 2號導線和5號導線的位置相互變換.從線束電感和電容參數矩陣的角度來看, 參數矩陣沒有產生新元素, 只是元素相對位置發生改變.以電容參數矩陣變換為例, 其變換公式如下:

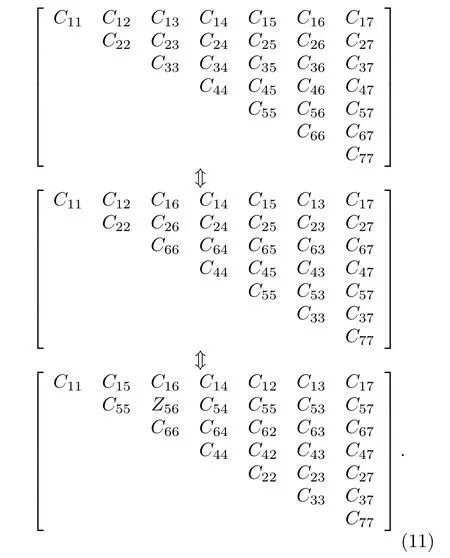
由(1)式—(3)式可知, 線束不同位置處的單位長度電容矩陣可以根據已知的單位長度電感和電容矩陣獲得, 這樣只需執行一次分布參數矩陣的計算即可.

(2)簡化導線半徑和對地高度

根據簡化線束的單位長度電感Leq和電容Ceq, 確立簡化線束的幾何截面結構, 即簡化線束半徑r和對地高度h.

簡化線束半徑: 計算簡化導線的半徑req, 根據(1)式理想導電平面上不確定性捆扎線束簡化導體自感計算表達式, 則等效導線的半徑req為

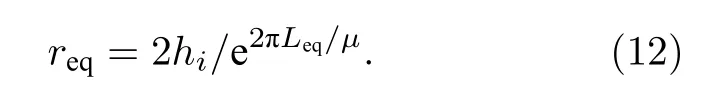
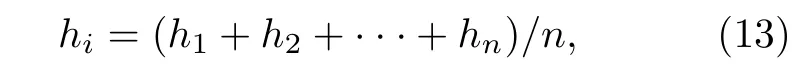
式中,d1,d2,···,dn為線束中各導線對地高度.

3.3 簡化線束模型終端負載的確立

由于共模干擾是線纜電磁干擾的主要因素, 在確立簡化線束的終端負載時, 本文主要考慮線束的共模負載, 即導線終端與參考地之間的阻抗(如圖7所示), 由n根導線組成的共模負載模型.

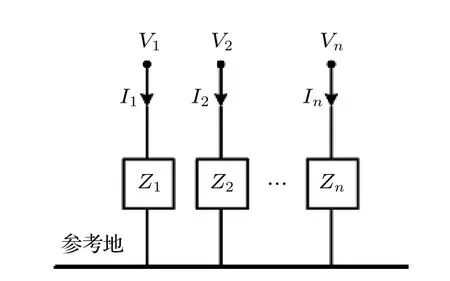
圖7 共模負載的確立Fig.7.Determination of the common mode load impedance.

圖7 中簡化線束模型的共模負載計算公式為

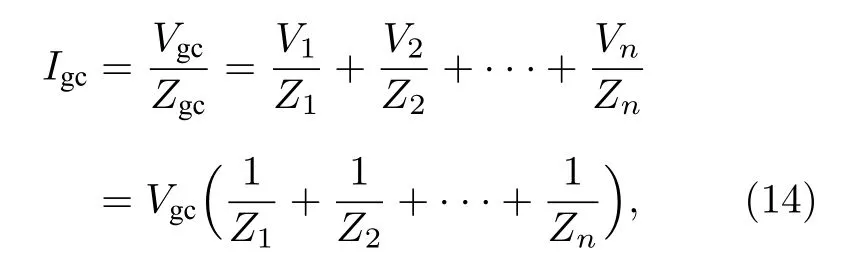
則

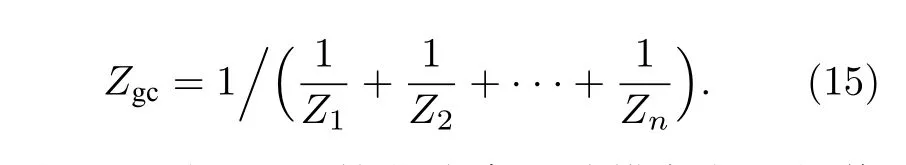
由(15)式可得, 簡化線束的共模負載阻抗值等于全線束中所有導線終端共模負載的并聯值.

4 數值算例驗證

4.1 圓弧不確定性捆扎線束

本文采用電磁仿真軟件CST (Cable Studio工作室)對本文方法進行驗證, 利用CST全波仿真方法求解計算平面波照射下圓弧不確定捆扎線束等效前后的電磁耦合效應大小.如圖8所示, 在CST中建立21根多導體不確定性捆扎線束模型,線束中所有導體長度為3/4個半徑為R= 825 mm的圓弧; 芯線具有相同的半徑r=0.2 mm, 絕緣層厚度為1 mm, 絕緣層介電常數為2.5, 相對磁導率為1.0.中間一排導線(編號2, 6, 11, 16, 20)距離地面高度60 mm.參考地面為長4000 mm, 寬4000 mm, 厚2 mm的PEC良導體.平面波入射方向沿y方向平行于參考地面, 采用線極化方式,電場方向沿x方向, 幅值為50000 V/m, 干擾源波形為CST默認脈沖激勵源.線束負載阻抗均為50 W.圖8中編號為1—21的導線近端端點坐標如表1所列.

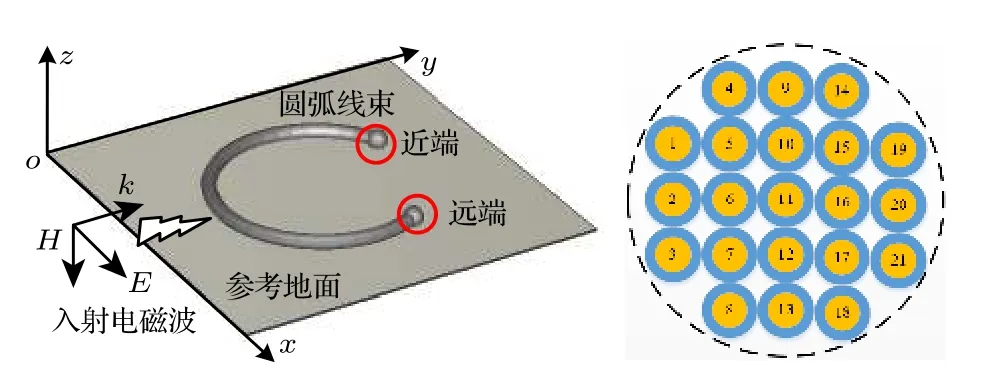
圖8 平面波照射下21根圓弧捆扎線束模型示意圖Fig.8.Schematic diagram of a 21-conductor circular arcshaped binding cable harness model illuminated by the plane wave.

使用高斯分布和樣條插值法獲取不確定性捆扎線束內21根導線的位置.首先, 通過線束兩端位置確立弧形線束的始端坐標, 確立捆扎線束初始位置處電容矩陣C(z) 和電感矩陣L(z).然后, 在MATLAB中使用高斯分布函數建立每根導線中心位置的隨機坐標.開始時, 在線長方向上依次將所有導線的N個截面在參考位置處進行填充, 從而建立不確定性捆扎線束模型.

表1 直角坐標系中21-線束模型近端位置(單位: mm)Table 1.Coordinates of each conductor near end of the 21-conductor cable harness (unit: mm).

基于簡化線束單位長度電感和電容矩陣計算結果, 根據簡化線束幾何截面參數建立方法可以得到簡化導體半徑為4 mm, 絕緣層厚度1 mm, 對地高度為60 mm.根據本文提出的不確定性捆扎線束廣義ECBM 方法, 簡化線束模型耦合電流值等于其全線束模型內各導線耦合電流之和, 21根不確定性捆扎線束模型等效前后近端和遠端負載上耦合電流對比曲線如圖9(a)和圖9(b)所示.

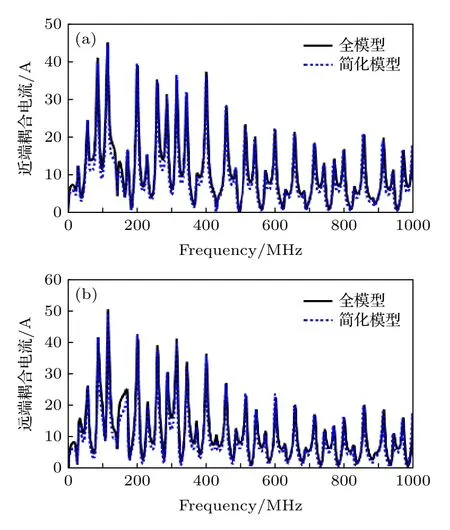
圖9 圓弧不確定性捆扎線束簡化前后負載耦合電流對比 (a)近端; (b)遠端Fig.9.Comparison of the load coupling current on the circular arc-shaped binding cable harness: (a) Near end;(b) far end.

從仿真結果看, 在0—1 GHz頻段內, 不確定性捆扎線束簡化模型近端和遠端負載耦合電流與其全模型耦合電流符合良好, 從而驗證了本文提出的廣義ECBM方法的正確性.

4.2 正弦不確定性捆扎線束

不確定性捆扎線束布線路徑呈正弦弧形, 如圖10所示.弧形路徑滿足函數mm, 其中t為線束長度方向位置坐標, 取值范圍為(0, 2000 mm).線束內導線參數不變, 中間一排導線(編號2, 6, 11, 16, 20)距離地面高度40 mm.外部電磁環境為平面波, 幅值和入射方向與圖8中保持一致.

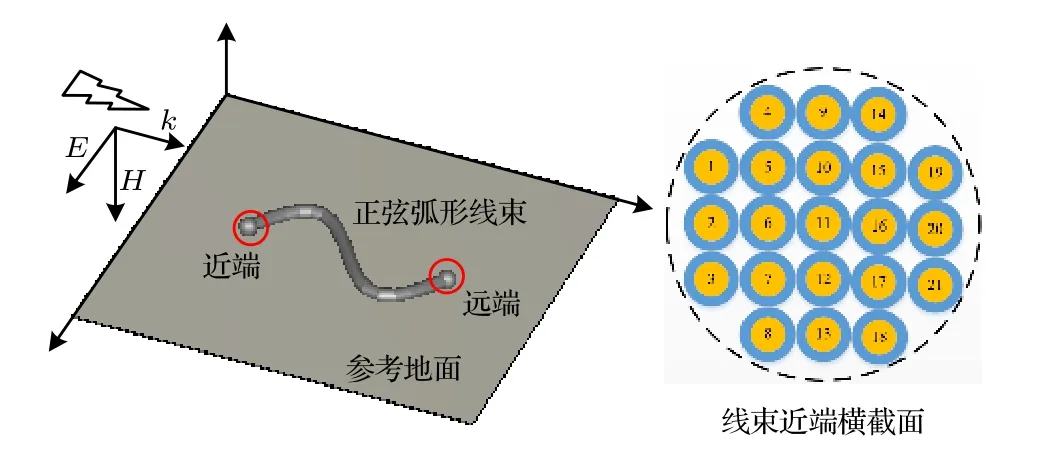
圖10 平面波照射下21根正弦弧形不確定性捆扎線束模型Fig.10.Schematic diagram of a 21-conductor sine arcshaped binding cable harness model illuminated by the plane wave.

根據本文提出的不確定性捆扎線束廣義ECBM方法, 21根正弦弧形線束模型簡化前后近端和遠端負載上耦合電流對比曲線如圖11(a)和圖11(b)所示.從仿真結果看, 在0—1 GHz頻段內, 不確定性捆扎線束簡化模型近端和遠端負載耦合電流與其全模型耦合電流符合良好, 再次驗證了本文提出的廣義ECBM方法的正確性.

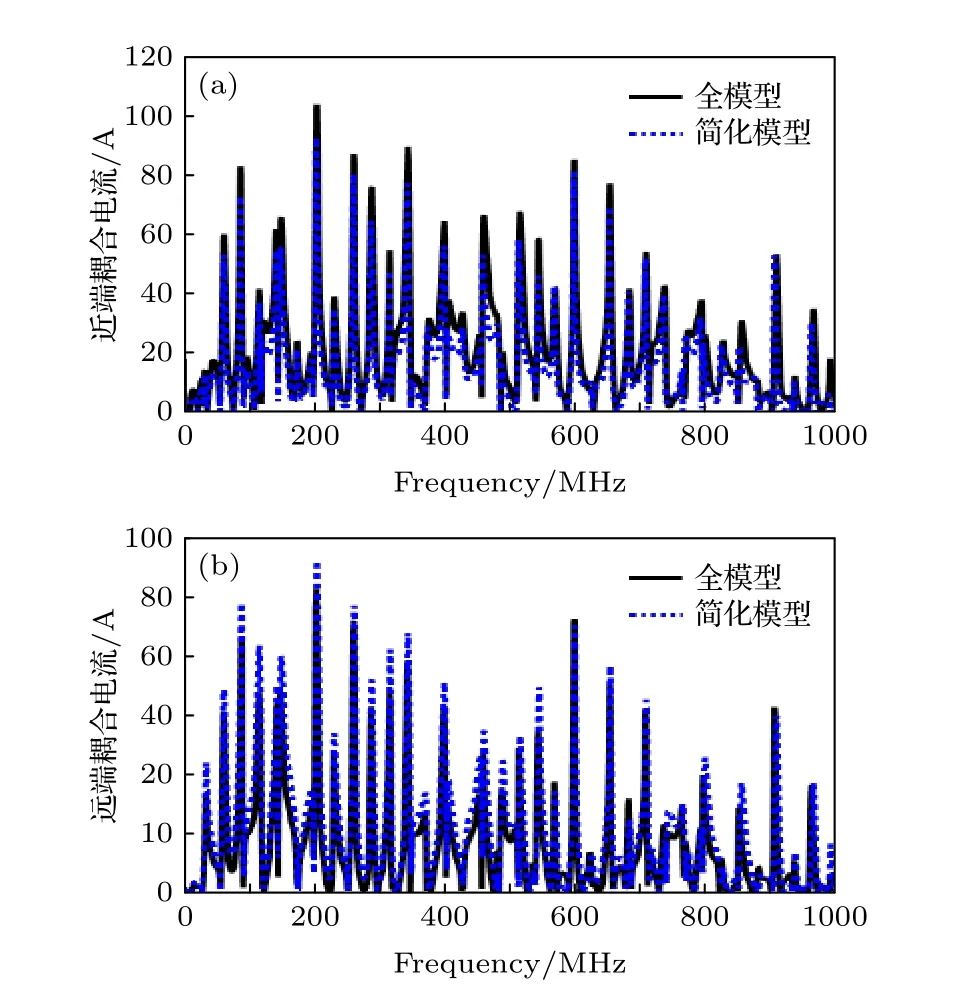
圖11 正弦不確定性捆扎線束簡化前后負載耦合電流對比 (a)近端; (b)遠端Fig.11.Comparison of the load coupling current on the sine arc-shaped binding cable harness: (a) Near end; (b) far end.

4.3 誤差分析

本文采用特征選擇驗證技術(FSV), 對完整模型和簡化模型之間的仿真結果進行評價[20,21].FSV技術根據特定標準顯示了兩組數據之間相關性.FSV技術評價指標主要包括: 總幅差測度(ADMtot)、總特征差測度(FDMtot)和總全局差測度(GDMtot).根據ADMtot, FDMtot和GDMtot大小對數據間符合程度劃分等級描述: excellent (0—0.1), very good (0.1—0.2), good (0.2—0.4), fair (0.4—0.8),poor (0.8—1.6)和very poor (> 1.6).

表2列出了圖9和圖11仿真結果的FSV技術評價結果.從表2可以看出, 圓弧和正弦捆扎線束等效前后對比結果評價良好, 進一步說明了本文方法的有效性.

表2 本文方法的FSV評價結果Table 2.The FSV evaluation results of the proposed method.

4.4 計算效率對比

表3列出了在相同仿真頻段范圍內本文廣義ECBM方法和全模型線束仿真計算時間.仿真中使用的計算機配置為: 處理器Inter(R) Core(TM)CPU i7-8700 @ 3.20 GHz, 內存8 G, 操作系統為Win 10 64位.從表3可以看出, 本文提出的不確定性捆扎線束廣義ECBM方法大大降低了線束建模難度, 有效提高了仿真效率.

表3 全模型和簡化模型仿真時間分析Table 3.Analysis time of the simplified and complete model.

5 結束語

針對機電系統復雜線束電磁耦合效應建模問題, 本文提出了廣義ECBM方法, 將不確定性捆扎線束模型簡化為單根線束模型, 考慮了線束內導線位置的不確定性.利用高斯分布和樣條插值獲取了不確定性捆扎線束內導線的位置, 利用導線子段之間存在換位關系求得線束的分布參數.基于理想導體平面上的多導體傳輸線電感和電容計算公式,得到了原線束模型的分布參數.由全模型與等效模型分布參數間的等價關系, 得到等效線束模型的電感和電容參數, 并依此確立了簡化模型的半徑和對地高度等幾何截面參數.最后, 通過圓弧和正弦不確定性捆扎線束數值算例, 驗證了本文提出的線束簡化建模方法的正確性.在保證計算精度的前提下, 本文方法有效解決了復雜線束由于“不確定性捆扎”帶來的建模難問題, 為機電系統內不確定性捆扎線束的電磁兼容問題分析提供了有效途徑.