大數據加密算法在數據安全保護中的應用研究

(中共陜西省委黨校(陜西行政學院)文化與科技教研部，西安 710075)

0 引言

大數據是指數據規模較大，無法使用現有技術進行存儲和處理的數據集，用戶的隱私和數據安全問題一直是大數據領域研究的重點。隨著大數據技術的逐漸成熟，大數據技術被廣泛的運用到各個領域，大數據加密算法和方案的研究受到廣泛關注。

在現有研究中，文獻[1]采用超混沌分組加密和AES混合加密方案，雖然提高了算法的執行效率，但是忽視了AES加密算法的S盒迭代循環周期短的問題，文獻[2]采用雙混沌系統設計出一個數據加密模型，雖然也能夠提高數據加密的效率和安全性，但是沒有考慮到AES算法。本研究基于以上內容，對兩組三倍混沌進行改進和AES算法進行改造生成兩個新的四維混沌系統和新的AES算法，采用兩個四維混沌系統設計出一個分組加密方案，最后在Hadoop平臺上與改進AES算法融合成一個加密算法。

1 Hadoop大數據平臺

Hadoop是一個分布式大數據平臺，主要由HDFS和MapReduce兩個核心組件組成，HDFS主要負責數據的分布式存儲，MapReduce主要負責數據的分布式計算[3]。

MapReduce會將從HDFS傳輸過來的數據集分成若干個獨立部分，然后由Map任務對這些獨立的部分分別進行并行運算來完成對它們的處理，運算的結果則會傳輸給Reduce任務[4]。一般情況下，中間過程的運算結果會存儲在本地磁盤中，只有最終的輸出結果和輸入會存儲在HDFS中。

2 兩個改進超混沌系統

超混沌系統相比混沌系統在加密領域具有更高的應用價值，因為其具有更為復雜的動力學行為[5]。

2.1 改進超混沌系統1

文獻[6]提出了一種三維連續自治的混沌系統，其狀態方程為：

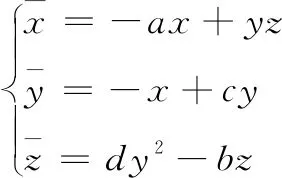
(1)

式(1)中，a，b，c，d為該三維系統的實際參數，x，y，z為該三維系統的狀態變量。該系統在a=20，b=5，c=10，d=7時會產生混沌吸引子，此時該系統會變成超混沌狀態，產生3個Lyapunov指數，分別為LE1=1.237 1，LE2=-0.029 1，LE3=-16.448 4。

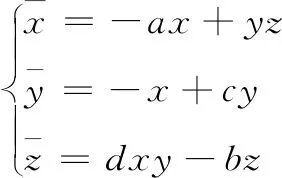
(2)

經過計算和分析，該系統在a=20，b=5，c=10，d=2時的3個Lyapunov指數為LE1=2.051 8，LE2=-0.017 2，LE3=-17.406 1，相比文獻[6]中提出的混沌系統，可以很明顯看出本研究的混沌系統的3個Lyapunov指數遠大于文獻[6]的混沌系統Lyapunov指數，因此本研究的混沌系統具有比文獻[6]混沌系統更復雜的動力學特性，比文獻[6]中的混沌系統更非常適合用于大數據加密研究。

但是，該系統存在計算資源消耗高和結構復雜等問題，為此，采用狀態反饋控制法，引入一個第四維的狀態變量w[7]，并將狀態變量w引入到式(2)中的的第二個方程中，能夠得到一個新的四維混沌系統:

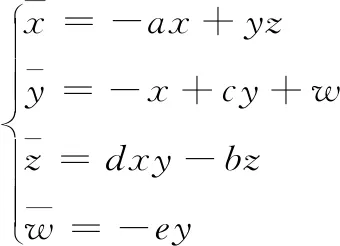
(3)

該系統相比傳統的超混沌系統，只有兩個非線性項，結構更加簡單，除此之外，在相同的計算資源下，能夠產生比文獻[6]更長的混沌序列，因此比文獻[6]的混沌系統更適用于大數據加密。

2.2 改進超混沌系統2

文獻[8]提出一個三維Bao混沌系統，其數學模型為：

(4)

該系統中包含兩個非線性項的連續自治微分方程，式(4)中，a，b，c為該三維系統的實際參數，x，y，z為該三維系統的狀態變量。該系統在a=20，b=4，c=32時會產生混沌吸引子，此時該系統會呈超混沌狀態，產生3個Lyapunov指數，分別為LE1=2.887 3，LE2=-0.011 5，LE3=-18.904 9。

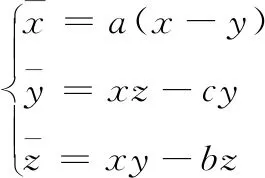
(5)

經過計算和分析，該系統在a=20，b=8，c=32，d=3，e=5.7時，的3個Lyapunov指數為LE1=4.294 2，LE2=-0.006 2，LE3=-24.335 9，相比文獻[8]中提出的混沌系統，可以很明顯的看出改進后的混沌系統的3個Lyapunov指數遠大于文獻[8]的混沌系統Lyapunov指數，因此改進后的混沌系統的動力學特性比文獻[8]更復雜，比文獻[8]更適合用于大數據加密研究。

同樣的在式(5)的基礎上引入一個第四維的狀態變量w和一個控制參數d，然后將反饋控制項添加到式(5)的第一項中，能夠得到一個四維超混沌系統：

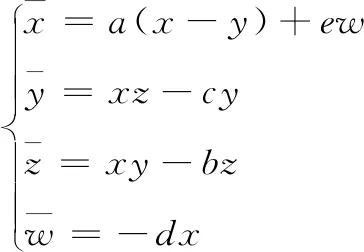
(6)

該系統在a=20，b=8，c=32，d=3，e=5.7時會產生超混沌吸引子，在系統結構、計算資源消耗上比文獻[8]的混沌系統更有優勢。

3 改進AES加密算法

S盒是AES算法的重要組成部分之一，而傳統的S盒迭代周期短，導致加密的安全性不高，存在被破解的可能，因此本研究對AES的S盒進行改進[9]。

3.1 S盒的結構和原理

在AES算法中，S盒運算是一種作用于狀態字節的可逆的非線性變換運算，其定義為：

(7)

式(7)中，ai ,j-1為ai,j在GF(28)域中的乘法域：

(8)

因為有關運算是在GF(28)域上進行，所以運算產生的計算結果也會在GF(28)域上，最終產生的S盒是由16×16個字節組成的矩陣，并且最終的結果具有非線性度，因為計算的過程使用了乘法逆[10]。

3.2 改進S盒方案

提高S盒的迭代周期方法有采用不同的仿射變換對、改變S盒的計算順序等方式[11]。因此本研究采用文獻[12]中的新仿射變換對(A7,6F)對傳統的S盒進行改進，改進的方法是采用新的仿射變換對(A7、6F)進行兩次仿射變化，兩次變換之間要求乘法逆。

4 大數據加密算法設計

4.1 兩組超混沌加密方案

在設計混沌密碼的過程中，當加密算法選擇的是連續時間混沌系統時，需要注意連續混沌序列離散化、密鑰參數選取對算法性能的影響[13]，除此之外，還要保證算法的安全性和實用性。基于以上內容，本研究的大數據加密方案如下：

(1)選取密鑰參數。選取密鑰參數的前提是混沌系統處于超混沌態，通過試驗和計算系統達到超混沌系統時的參數，保持參數不變，選取的密鑰參數為上述兩個超混沌系統的8個初始值，這樣能夠保證算法具有足夠大的密鑰空間[14]。

(2)對混沌序列進行預處理。第一步對混沌系統進行離散化處理，本研究采用的是四階RungeKutta法，第二部舍棄迭代序列的前100個值，舍棄前100個值的原因是為了讓生成的混沌序列的隨機性高[15]，第三步對混沌序列進行相關運算，使得混沌序列能夠適應于字節加密，計算方法為：

(9)

式(9)中，mod為模去余數運算，i=1,2，??為向下取整運算，px(i)(k)，py(i)(k)，pz(i)(k)，pw(i)(k)為經過計算得到的8個混沌序列，它們的取值范圍為[0,256]。

(3)混淆處理。超混沌系統生成的狀態變量會存在一定的關聯性，在被攻擊時，這些關聯性會為攻擊者提供一定的信息，會提高被攻破的概率，為了提高算法的性能，減少被攻破的概率[16]，本研究對生成的兩組混沌序列進行混淆處理，混淆處理的方法為：

(10)

式(10)中，⊕為異或運算符號，pi(k),i=1,2,3,4為經過運算后得到的可以用于大數據加密的超混沌序列，最終得到的這些序列之間的關聯性全部被破壞，從而提高了算法的安全性[17]。

(4)分組加密。將步驟(3)中得到的4個序列對數據進行加密，加密方法是將數據按字節分組，每4個字節為一組進行加密，具體的加密過程為：

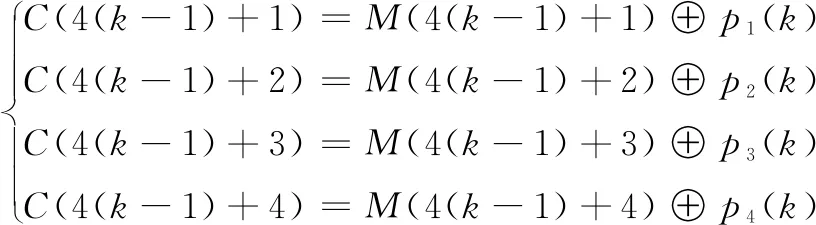
(11)

式(11)中，M為需要進行加密處理的數據明文，C為經過超混沌分組加密后得到的密文。加密方案如圖1所示。

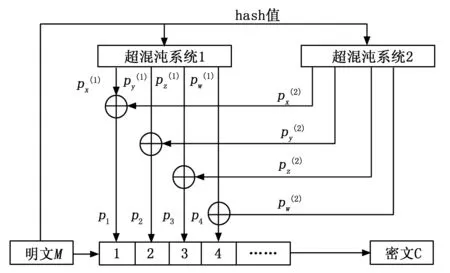
圖1 超混沌系統加密方案

4.2 基于MapReduce的超混沌系統和改進AES的混合加密算法

本研究的加密算法是在Hadoop大數據平臺上實現的，采用Hadoop平臺中的MapReduce編程模塊對加密算法進行編程，MapReduce由Map和Reduce兩個函數組成，其中Map函數負責將上述超混沌數據加密和改進AES算法進行融合[18]，Reduce函數負責在數據加密完成后的將所有的數據合并。具體步驟為：

(1)對大數據集進行分片處理，將存儲在HDFS上的大數據集按照Hadoop2.0的默認大小進行分塊，每塊128 MB。

Output:

call farctional-hyperchaos-Ⅰ(KCHAOS)

call farctional-hyperchaos-Ⅱ(KCHAOS)

C(4(k-1)+1)=M(4(k-1)+1)⊕p1(k)

C(4(k-1)+2)=M(4(k-1)+2)⊕p2(k)

C(4(k-1)+3)=M(4(k-1)+3)⊕p3(k)

C(4(k-1)+4)=M(4(k-1)+4)⊕p4(k)

call AES-encrypt(KAES)

其中：KCHAOS為超混沌系統密鑰，KAES為改進AES算法密鑰。

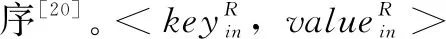
(4)數據合并完成后，會存儲在HDFS上，存儲完成后即完成整個加密過程。

同樣的解密算法的設計基本與加密算法相同，唯一不同的是解密算法中的Map函數進行的是解密操作而不是加密，只有當解密密鑰和加密密鑰完全匹配時，才會得到原始的明文數據，如果不能完全匹配，則不能得到明文數據[21]。因為采用了具有更加復雜動力學的超混沌系統和迭代周期長的AES算法，使得本研究的加密算法的安全性得到了很大的提高。

5 試驗結果與分析

選擇在實驗室內采用高性能計算機對本研究的算法進行驗證，計算機的硬件配置CPU為，inter corei7-9700H，運行內存為3 200 MHz 8 G×2,硬盤大小為512 G固態。首先需要部署多個虛擬機，虛擬機的布置采用的是VMware workstation 12軟件，虛擬機的配置為單核CPU和1 GB的運行內存，然后再虛擬機上部署Hadoop大數據平臺，Hadoop的版本為2.7.3，算法的編程采用的是JAVA，JAVA版本為Jdk8，IDE的開發環境為Eclips3.8。試驗所用的數據為大小為1 GB和2 GB的大數據集，采用Map對其進行默認分塊，每塊的大小為128 MB。

首先對本研究算法的密鑰長度進行驗證，驗證方法為對比驗證，對比的對象為文獻[1]、文獻[2]、文獻[6]和文獻[8]中的加密算法，本研究的加密算法的密鑰長度為超混沌系統的長度和改進AES算法長度之和，本研究將兩個超混沌系統的初始值作為超混沌系統密鑰參數，密鑰空間可以表示為：

KCHAOS∈{x1(0),y1(0),z1(0),w1(0),x2(0)y2(0),z2(0),w2(0)}

這里設置密鑰的精度為10-15，然后選取雙精度的密鑰參數，通過計算可以得到超混沌系統的密鑰長度為432 bit，在再加上改進AES算法的256 bit，一共為688 bit。將本研究算法的密鑰長度與其他文獻算法的密鑰長度進行對比，可以得到表1數據。

表1 密鑰長度對比

從表中數據可以看出，本文算法的密鑰長度明顯高于其他算法，密鑰長度能夠影響密文被破譯的難度，密鑰的長度越長，則被破譯的可能性就越低，算法的安全性就越高。

然后對本文算法的效率進行驗證，將本文算法中的超混沌加密方案和改進AES算法的效率分別進行驗證，采用兩種算法對上述1 GB和2 GB大小的數據集分別進行加密，逐步增加計算節點，統計不同節點下的加密時間，可以得到圖2的加密時間對比圖。

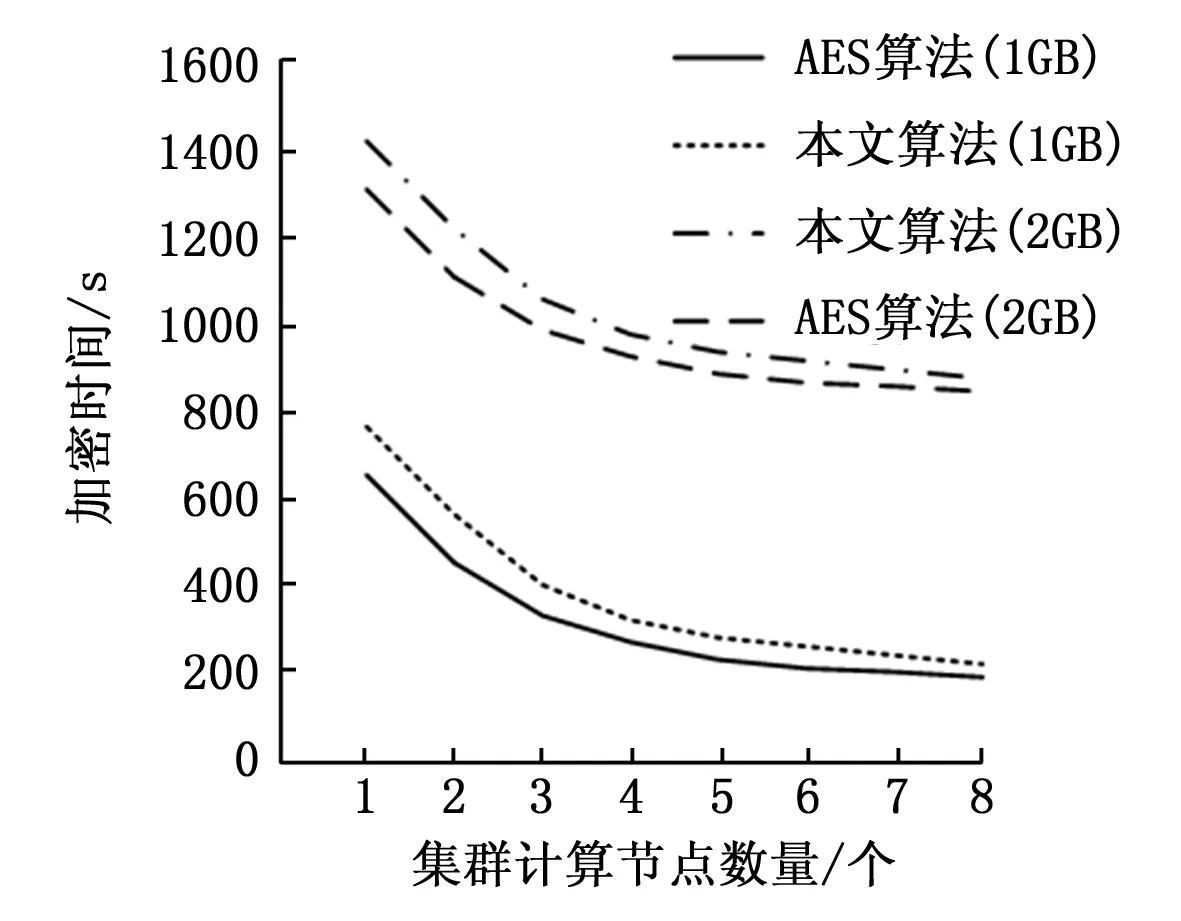
圖2 加密時間對比圖

從圖2中可以看出，雖然本研究的算法計算時間略微高于AES算法，但是隨著計算節點的增加，本研究算法的計算效率顯著提高。

最后對算法密鑰的敏感性和統計性進行分析，密鑰的敏感性決定算法的安全性，試驗結果表明，只有當密鑰完全匹配時，才會得到明文數據。當密鑰的參數誤差為10-15時會產生雪崩效應，無法獲取明文數據，并且會生成跟明文數據具有較大差異的密文，此時的密鑰參數解密數據直方圖如圖3所示。

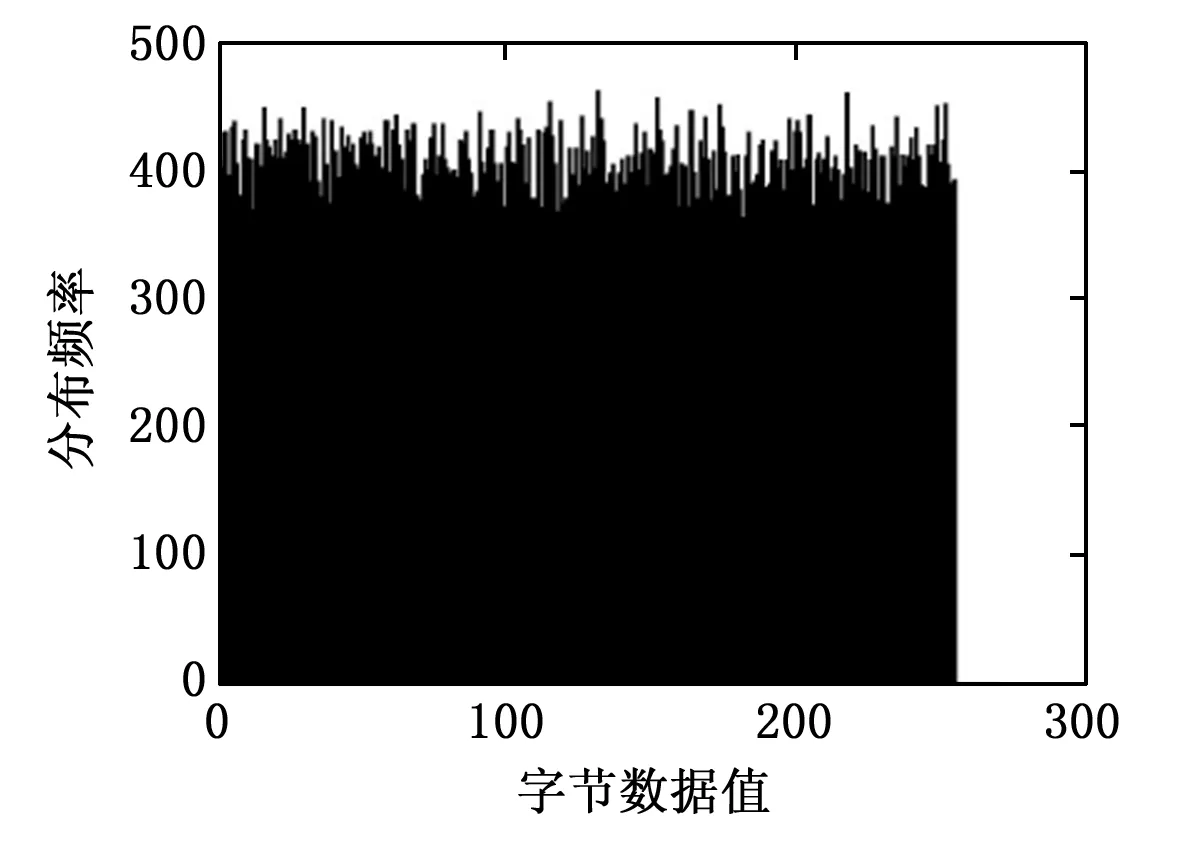
圖3 微小誤差下的密鑰參數解密數據直方圖

從圖中可以看出本研究算法的密鑰敏感性優秀，在達到臨界值后能夠產生雪崩效應，使得破譯的難度增大。

加密前后的數據字節數據值對比如圖4所示。

圖4 加密前后的文本數據統計圖

從圖中可以看出，原始具有一定規律分布的明文數據經過本研究算法的加密之后呈無相關性的隨機分布狀態。

綜上所述，本研究的大數據加密算法性能優秀。

6 結束語

本研究將利用MapReduce將雙超混沌加密算法與改進AES算法合并生成一個新的加密算法，通過試驗證明了算法的可行性，并得出以下結論：

1)數據加密中密鑰的空間大小會影響加密算法的安全性，本研究將兩個三維混沌系統進行改造生成了兩個四維混沌系統，提高了混動加密方案的密鑰長度。

2)傳統的AES加密算法的迭代周期短，可能會存在被破譯的風險，本研究采用新的仿射變換對生成一個新的S盒序列，提高了AES算法的迭代周期。

3)混沌系統具有非常復雜的動力學特性，不僅能夠用于數據加密，還能用于其他類型文件的加密，系統的維數越高，動力學特性越復雜，加密效果越好。

實驗結果表明，本研究的數據加密算法具有密鑰空間大、安全性能高，加密效率高等優勢，在網絡數據安全保護方面具有一定的研究價值，但是由于人為疏忽，難免會存在一些問題，在后續的研究中需要進行相應的改進和完善。