UWB精確定位自適應無跡卡爾曼濾波算法

王孜洲，臧利國，唐一鳴，賈鵬，王德海

（1.211167江蘇省 南京市 南京工程學院 汽車與軌道交通學院；2.211167江蘇省 南京市 南京工程學院 自動化學院；3.211167江蘇省 南京市 南京工程學院 電力工程學院）

0 引言

隨著位置服務的快速發展，人們對高精度定位技術的需求越來越高。定位技術廣泛存在于生活的方方面面，在工業生產、日常生活中發揮著巨大的作用。超寬帶定位技術（UWB）是近年來興起的一項室內定位技術，以非正弦波窄負脈沖傳輸信號。其抗多徑能力強，定位精度高，且對信道衰弱不敏感，難以截獲，成為最受關注的定位技術之一。

然而在實際應用中往往存在障礙物遮擋、金屬干擾等情況，會給UWB測距帶來較大誤差（NLOS誤差），嚴重影響UWB定位精度。為抑制NLOS誤差，提高定位精度，鮑小雨[1]等提出了一種改進的擴展卡爾曼濾波（IEKF）算法，通過實際觀測值和預測值的差值大小，確定是否存在NLOS誤差，若存在誤差，則將濾波增益設置為零，從而減小NLOS誤差對定位的影響。試驗顯示，該系統一定程度減小了NLOS誤差，但該方法依賴于閾值的設定，且誤警率較高，難以應用于實際工程中；李旭虹[2]等提出一種改進的無跡卡爾曼濾波算法，以聯合定位的初始坐標作為濾波觀測值，并在無跡卡爾曼濾波的更新方程中直接減去NLOS誤差項，避免了UKF濾波的發散。此種方法在建模時，將NLOS誤差假設為服從指數分布，然而實際測量中，NLOS誤差并非完全服從指數分布，因而濾波精度有所下降。

針對上述問題，為保證誤差抑制效果，本文首先對信道環境進行鑒別，若為LOS環境，則進行無跡卡爾曼濾波；若存在NLOS誤差，則針對性地引入自適應因子，對協方差進行修正，從而減小誤差。

1 TOA的定位原理和誤差模型

1.1 TOA定位原理

基于到達時間（TOA）定位利用測量信號在基站和標簽之間的到達時間，求出每個基站與標簽之間的距離，進而通過距離實現定位[3]。一般采用3個基站進行定位，其定位模型如圖1所示。

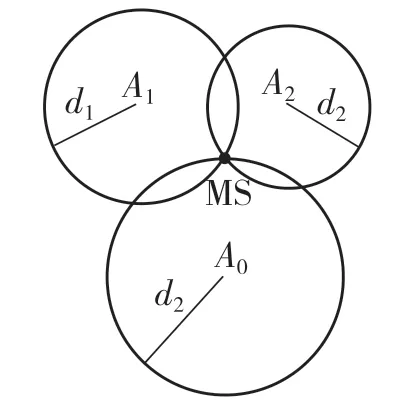
圖1 TOA定位原理Fig.1 Positioning principle of TOA

圖1中，A0，A1，A2為UWB基站位置；MS為標簽位置；測得基站A0，A1，A2與標簽MS的距離分別為d0，d1，d2；分別以基站為圓心、距離為半徑作3個圓，三圓交點即為標簽MS的位置。設3個基站坐標為（x0，y0），（x1，y1），（x2，y2），標簽坐標為（x，y），根據定位模型可列如下方程：

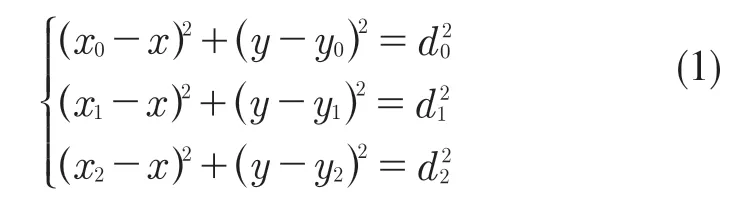
求解可得

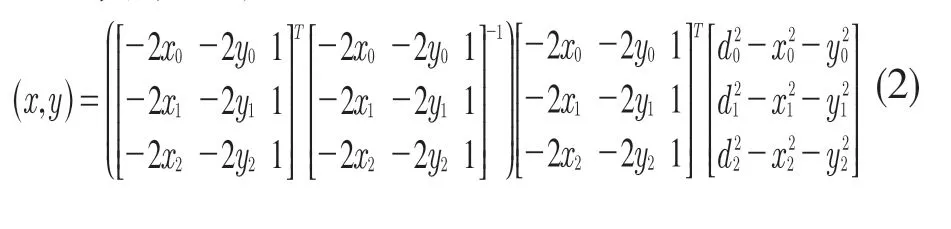
1.2 誤差模型

在NLOS環境下，直達單徑分量DP到達基站需經過障礙物，由于障礙物的介電系數大于1，會給測距模型帶來附加時延[4]。通常認為，此附加時延會導致正均值的隨機誤差，定位結果由點坐標變為如圖2所示的陰影區域，大大增加了定位的不可信度，同時提高了計算的復雜程度，導致計算效率降低。

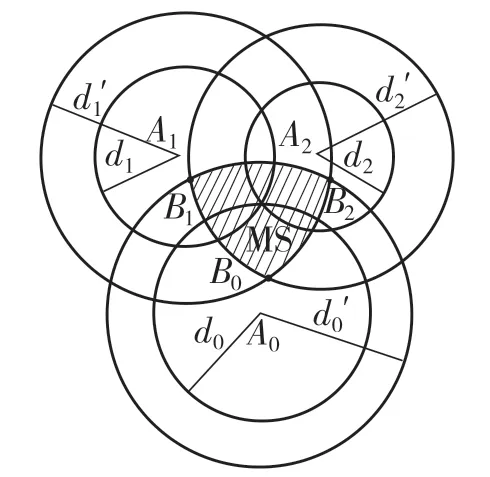
圖2 定位誤差模型Fig.2 Positioning error model

設陰影部分3個圓兩兩相交的3個交點為B0，B1，B2，坐標分別為，，為減小計算量，將基站設置于等邊三角形的3個頂點處，以兩點 A1，A2連線為X軸，連線中點為原點建立坐標系。

交點坐標可由兩圓聯立方程求解：

同理，可求出B1，B2的坐標，根據坐標算出 B0，B1，B2三點與實際標簽位置的距離為T0，T1，T2。距離公式：

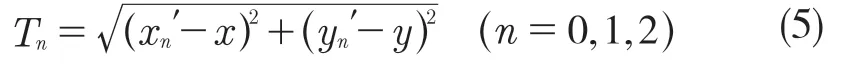
由此得出，NLOS環境下引入的定位誤差可達max（T0，T1，T2），具有極大的不確定性，大大減小了UWB的定位精度。

2 NLOS信道鑒別

由式（5）可知，NLOS誤差的存在會給UWB定位帶來極大的干擾。為保證誤差抑制效果，本文采用峭度作為參數鑒別UWB信道環境，若峭度參數異常，則說明存在NLOS誤差，便可引入自適應因子，有針對性地剔除NLOS誤差，從而保證定位精度。

UWB信號在IEEE802.15.4a標準下，信道沖激響應（CIR）可表示為[5]

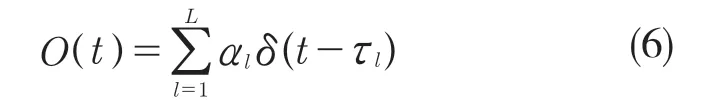
式中：l——第l條多徑；L——多徑總數；al，τ1——第l條路徑的幅度增益和時延；δ（x）——單位能量的單徑脈沖函數，其性質如下：

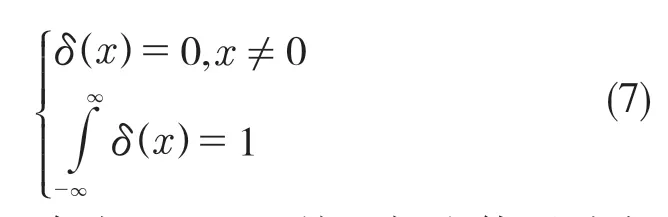
為鑒別是否存在NLOS環境，提出使用峭度作為衡量信道狀態的參數。峭度K定義為波形四階矩和二階矩平方的比值，即

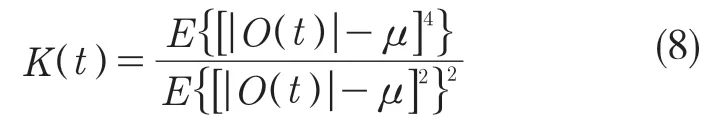
式中：μ——t時刻O（t）的均值，峭度作為信號的歸一化四階矩，對信號中的沖擊特征尤其敏感。

四階矩定義數據的峰度表征數據在均值處的峰值高低；二階矩即方差，表征數據的離散程度。峭度作為四階矩與二階矩的比值，可以表征數據相對于正態分布是陡峭還是平坦。對于高K的數據，傾向于在均值附近有更明顯的峰值，下降更迅速，數據更聚攏；對于低K的數據，傾向于在均值附近有更平坦的峰值，下降緩慢，數據更為離散[6]。一般LOS環境中因為沒有阻擋，數據變化更為劇烈，傾向于有更高的峭度；NLOS環境中數據變化較為緩慢，傾向于有更低的峭度。故峭度可作為衡量NLOS誤差的參數，表示如下；

式中：thresh——設定的閾值，因K=3時，波形具有正常峰值（零峭度），故取thresh=3。

3 自適應無跡卡爾曼濾波算法

3.1 定位模型

根據TOA定位原理建立定位模型。將基站A0，A1，A2固定，以A1，A2連線的中點作為原點O建立空間直角坐標系。標簽MS的狀態向量分別由標簽的平面坐標(x,y)和在方向上的速度vx、vy構成，可列狀態方程如下：

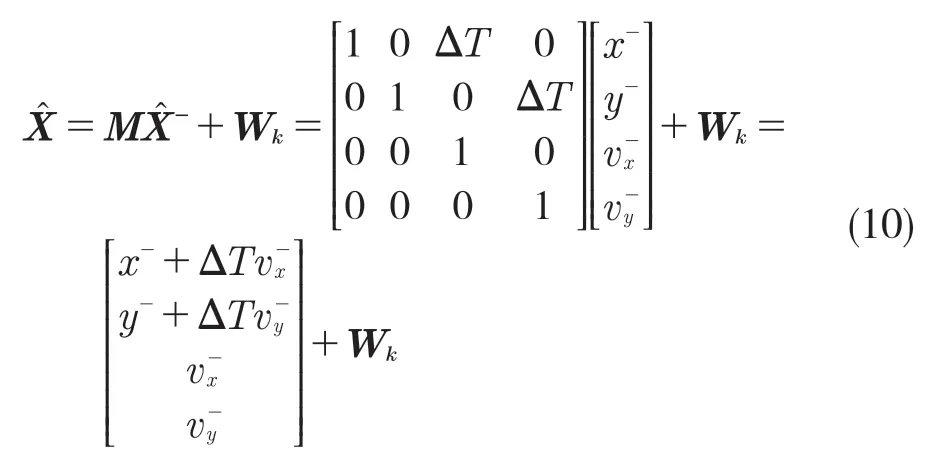
為使UWB的精度提高，可采用數字濾波算法優化定位數據。

3.2 標準UKF算法

卡爾曼濾波（KF）是目前應用廣泛的數字濾波技術，其利用上一系統狀態的數據和量測數據，通過線性系統狀態方程求出當前狀態最優估計值，在遞歸過程中提高預估精度[7]，但是，由于計算時必須通過線性系統狀態方程，所以，只適用于高斯線性模型。

對于非線性濾波問題，在卡爾曼濾波的基礎上主要有兩種發展：擴展卡爾曼濾波（EKF）算法和無跡卡爾曼濾波（UKF）算法。其中，EKF的核心是通過泰勒展開來處理非線性狀態方程和觀測方程，只取泰勒展開式的一階項來實現線性化[8]。但EKF也只適用于線性化較弱的系統方程，否則同樣會導致濾波器性能下降，影響其收斂性。而UKF的核心是利用UT（Unscented Transform）變換來對均值和協方差進行處理，從而避免線性化帶來的誤差。相比EKF,UKF不需要計算非線性函數的Jacobi矩陣，計算量大大減少，且UKF沒有忽略高階項，計算精度更好，適用性也更強（例如：UKF可以應用于復雜的NLOS環境）。

首先對濾波進行初始化：

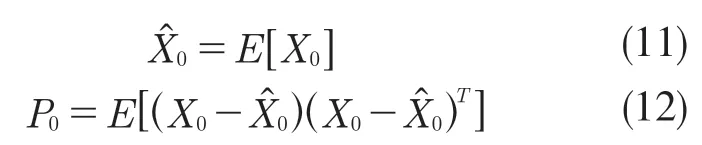
選取2n+1個Sigma樣本點，n由研究對象的狀態維數決定，本文主要研究UWB定位模型，可取n=2，選取方式如下：

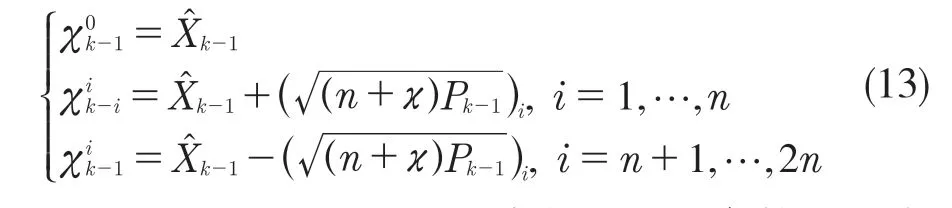
式中：χ——調整逼近的精度的尺度參數，適當調整可提高精度，且其中，α——一個較小的正數，取值范圍10-4≤α＜1，常取0.001，確定周圍Sigma樣本點的分布情況；β——有關狀態分布的參數，在高斯分布時最優取值為2；λ——比例因子，通常取0或3-n。對于上述α，λ，β這3個參數，都可以適當調節來提高計算過程中的估計值和方差的精度[9]。

UKF算法主體主要分為3個步驟，分別是預測更新、迭代更新和量測更新[10]。預測更新中，先對Sigma樣本點進行非線性變換，接著根據變換后的Sigma樣本點計算預測估計值和預測協方差

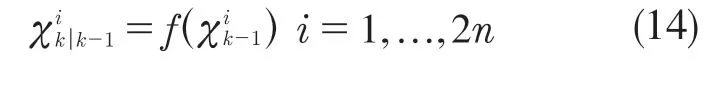
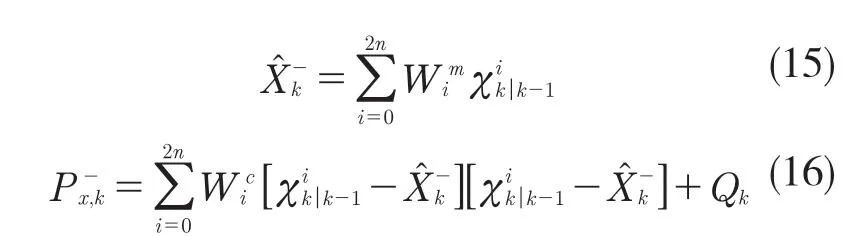
式中：Wim，Wic——計算均值和協方差的權值，計算方法如下：

3.3 自適應UKF

對于標準UKF，雖然相比EKF可以更好地處理非線性系統，但是，如果存在系統數學模型誤差或者系統噪聲特性不精確等情況，極有可能影響濾波的精度，甚至導致濾波的發散。此外，初始化的取值對UKF算法也存在影響，如果取值存在誤差會導致濾波估值的精度下降、收斂速度慢。針對以上存在的問題，本文采用了一種自適應UKF算法[11]。

首先，針對UKF算法在不同測量環境需要自適應的程度不同，需要一個隨環境變化的自適應因子，為此構建了測量殘差向量：

式中：yk——該時刻UWB的真實測量值；測量的估計值。當系統預測出現異常，或與系統模型不符，為使濾波保持精度，可引入自適應因子[12]，構建如下：

式中：μk——所構建的自適應因子（0＜μk≤1），可判別濾波中是否存在狀態模型誤差，并且對誤差有自適應調節的作用。

將構建的自適應子加入標準UKF中，可對其進行修正

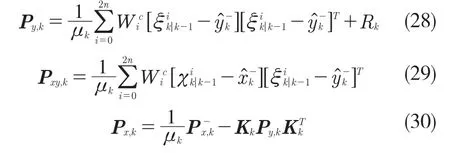
由以上分析可知，當系統模型等都正常時，μk=1，對濾波結果沒有影響；當初始值的選取可能存在異常或是狀態模型存在偏差時，μk＜1，即濾波結果對預測的估計值信任程度下降；當狀態模型錯誤時，μk無窮接近于0，與其相關的值可完全舍棄[13]。因此，當濾波結果出現異常時，系統能做出自適應調節，減少異常值造成的影響，使最終得出的濾波結果相對準確。

恰當設置自適應因子，能夠對狀態方程預測值和測量值的權比進行自適應平衡，也能降低系統模型誤差對濾波的影響。此外，自適應因子在濾波的遞歸過程中不斷對增益矩陣進行修正和調節，在此過程中UKF算法的抗差能力也得到提高。

4 試驗與分析

為驗證本文算法對UWB定位數據的優化效果和對NLOS誤差的修正能力，在10 m×10 m的實驗室環境中，進行了模擬NLOS試驗。試驗采用典型帶寬為500 MHz的DWM1000射頻模塊，通信速率6.8 m/s，發射功率為-62～-35 dBm/MHz。

UWB的定位環境如圖3所示。基站 A0，A1，A2沿邊長為6 m的等邊三角形頂點放置，虛線表示標簽MS運動軌跡。

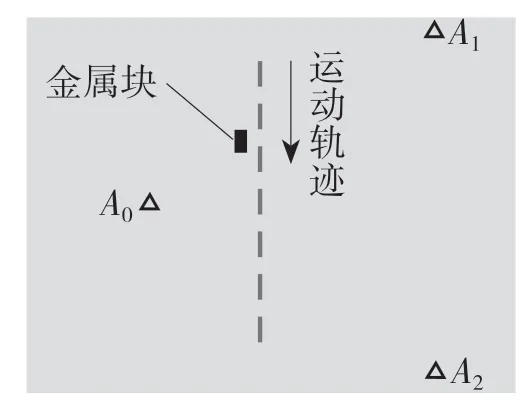
圖3 試驗環境Fig.3 Test environment

在基站A0與軌跡之間插入一塊金屬塊，當標簽、金屬塊和基站A0三者在同一直線上時，介電系數大于1的金屬塊會干擾直達單徑分量DP的傳播，形成強NLOS環境。分別采用傳統定位算法和本文算法進行定位試驗，試驗結果見圖4。

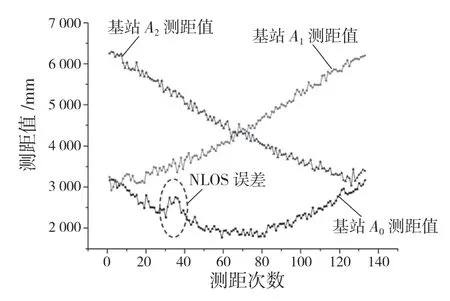
圖4 基站測距值Fig.4 Base station ranging value

圖4為基站 A0，A1，A2與標簽MS的測距值，從圖中可看出第30次到第40次測距中，基站A0受金屬塊影響，測距值出現突變，表現在定位結果中即如圖5所示。

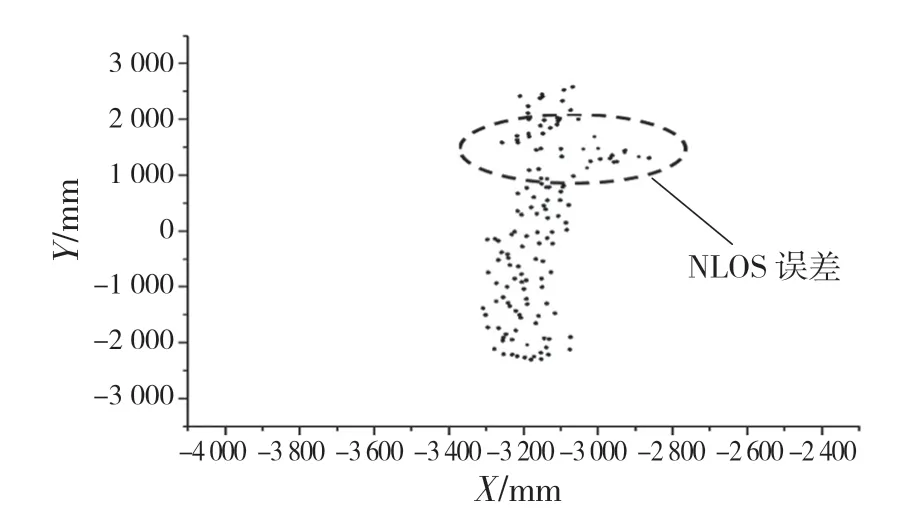
圖5 原始定位結果Fig.5 Positioning results

圖5為傳統算法定位結果，可看出數據在y=-1 500 mm處開始出現異常，隨后定位出現較大誤差，最大誤差值達到了335.89 mm；圖6為本文算法定位結果，顯然數據波動更小，并且原NLOS誤差處相對平緩，最大誤差僅為158.83 mm，相比傳統算法最大誤差下降了52.7%。為對比整體定位結果，計算了RMSE（均方根誤差）值與MAE（平均絕對誤差）值。參見表1。

其計算方法如下:

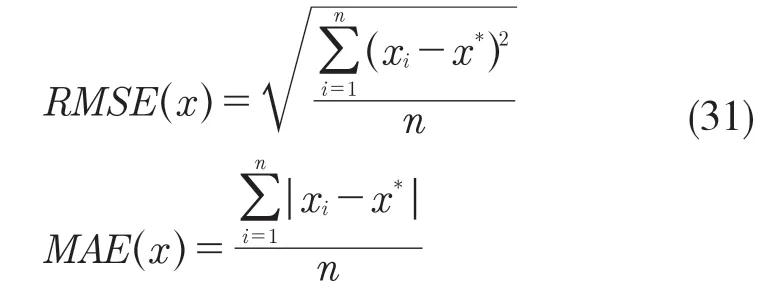
式中：x*——標簽MS在x方向的真實距離；xi——第i次定位中本文算法解算出的標簽MS在x方向的測量值；n——測量總次數；RMSE值——誤差平方均值的平方根，一般用來表示定位數據的離散程度；MAE值——誤差絕對值的平均，可用來表示定位數據的整體誤差。

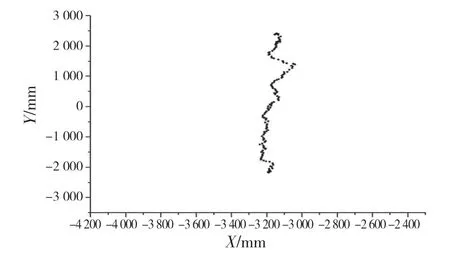
圖6 本文算法定位結果Fig.6 Positioning results of the algorithm in this paper

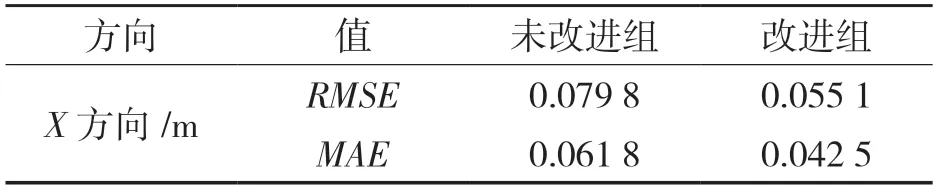
表1 試驗結果Tab.1 Test results

試驗表明，本文提出的算法對UWB的數據優化明顯，并且能夠準確鑒別并修正NLOS誤差。

5 結語

UWB作為當前精度最高的室內定位技術，其發射信號功率譜密度低，截獲率低，但受環境影響顯著。本文根據UWB的TOA定位原理，分析了UWB在NLOS環境下的誤差模型。并通過計算峭度判別UWB信道環境，對于參數正常的情況，判定為LOS環境，采用適用于非線性模型的標準無跡卡爾曼濾波算法進行濾波；對于參數異常的情況，判定為NLOS環境，在UKF算法的基礎上加入自適應因子修正增益矩陣，進而減小NLOS誤差。經試驗驗證，該算法有效實現了對定位結果的優化和對NLOS誤差的修正，提高了UWB的定位精度。